В прямоугольный сосуд с водой имеющий площадь основания
Задачи, тесты
Е. М.
Раводин,
, МОУ СОШ № 2, г. Прокопьевск, Кемеровская обл.
Окончание. См. № 5,
8/2010
18. Прямоугольная коробочка из жести массой m = 76 г с дном площадью S = 38 см2 и высотой H = 6 см плавает в воде. Определите высоту h надводной части коробочки.
Решение. Коробочка плавает, если действующая на неё сила тяжести равна по модулю действующей на неё силе Архимеда: mg = FА, причём FА = Vпчgρв, где 
– объём погружённой части коробочки. Подставляя числовые данные, получаем 
Отсюда глубина погружения коробочки равна
Значит h = H – x = 4 см.
19. Льдина плавает на поверхности пресной воды. Какую часть составляет объём подводной части от объёма всей льдины? Если задача не решается в общем виде, то, для упрощения, примите объём льдины равным 100 м3. Плотность льда 900 кг/м3.
Решение. Раз льдина плавает, то её сила тяжести равна по модулю силе Архимеда: mg = FА, т. е.:
20. На поверхности широкого озера лёд имеет толщину 2 м. Какой минимальной длины надо взять верёвку, чтобы зачерпнуть кружкой воды из проруби?
Решение. Так как озеро широкое, то лёд на его поверхности может только плавать, а не держаться за берега за счёт примерзания к ним. Согласно решению задачи № 19, в проруби под поверхностью воды окажется 0,9 толщи льда, т. е. 0,9 · 2 м = 1,8 м, а над поверхностью воды 0,2 м = 20 см. Для зачерпывания воды с такой глубины верёвка не нужна.
21. В стакане с пресной водой плавает кусок льда. Изменится ли уровень воды, когда лёд растает? Рассмотрите дополнительно случаи: когда в лёд вмёрзла дробинка; когда в лёд вмёрз пузырёк воздуха.
Решение. Лёд плавает, если его вес равен весу жидкости в объёме погружённой части. Образовавшаяся изо льда пресная вода имеет тот же вес, что и лёд, и, следовательно, точно заполнит объём, который вытеснял плавающий лёд. Значит, уровень воды не изменится.
Если во льду была дробинка, лёд вытеснял больше воды, чтобы поддерживать на плаву дробинку. Когда лёд растаял, дробинка утонула (её вес больше веса вытесненной ею воды), уровень воды понизился.
В случае вмёрзшего пузырька уровень воды после таяния льдины практически не изменится. Хотя, если подсчитать точно, уровень воды несколько понизится, т. к. масса воздуха в пузырьке хоть и мала, но не равна нулю.
22. В прямоугольный сосуд с водой пустили плавать модель судна массой m = 4 кг. На сколько при этом повысился уровень воды, если площадь дна сосуда S = 2000 см2?
Решение. Вес сосуда при опускании в него модели увеличится на вес модели mg. Это увеличение веса можно интерпретировать как следствие подъёма уровня воды на ∆h и, следовательно, увеличения силы давления воды ∆Fд = ρвg∆hS. Отсюда:
23. Кусок парафина массой m = 200 г плавает на границе раздела воды и бензина. Определите объём V1 надводной части бруска. Плотность парафина 900 кг/м3, бензина 700 кг/м3.
Решение. Если парафин плавает, то сила тяжести равна сумме сил Архимеда в обеих жидкостях: mg = Vвρвg + V1ρб g, где Vв – объём, погружённый в воду, V1 – искомый надводный объём (в бензине). Общий объём парафина 
Решая совместно оба уравнения, получаем:
24. Кусок льда, внутрь которого вморожен шарик из свинца, плавает в цилиндрическом сосуде с водой. Площадь дна сосуда S. Какова масса шарика, если после полного таяния льда уровень воды в сосуде понизился на H? Плотность свинца ρ1, плотность воды ρ2.
Решение. На плавающую льдину со свинцовым шариком действует бóльшая сила Архимеда, чем на такую же льдину без шарика, т. к. она тяжелее на силу тяжести шарика mg. Следовательно, объём вытесняемой в первом случае воды больше, чем во втором, на 
Но когда льдина растает, шарик упадёт на дно и займёт объём V1 = m/ρ1. Общее уменьшение объёма воды в конечном счёте ∆V = ∆Vп – V1. Так как ∆V = SH (по условию), то приходим к уравнению: 
25. Корона царя Гиерона в воздухе весит P1 = 20 Н, а в воде P2 = 18,75 Н. Вычислите плотность вещества короны. Была ли она из чистого золота? Дополнение: найдите, сколько золота и сколько серебра было в короне. Плотность золота округлённо принять 20 000 кг/м3, а серебра 10 000 кг/м3.
Решение. Для оценки добросовестности мастера найдём плотность короны по формуле 
полученной при решении задачи 9 (см. № 5/2010):
– корона не из чистого золота.
Чтобы найти состав короны, используем два факта: 1) общая масса короны m = mз + mс; 2) общий объём короны V = Vз + Vс (индексы «з» и «с» относятся к золоту и серебру соответственно). Заменяя объёмы их выражениями через массы и плотности, получаем систему из двух уравнений:
Решение
Опуская громоздкие промежуточные вычисления, запишем ответ:
26. Какую силу надо приложить к пробковому телу массой 400 кг, чтобы удерживать его, когда оно целиком погружено в воду? ρп = 200 кг/м3; g = 10 м/с2.
Решение. Сила тяжести тела mg = 4000 Н направлена вниз, сила Архимеда направлена вверх и равна
Чтобы удержать тело в воде, надо приложить направленную вниз силу F = FА – mg = 16 кН.
27. Чугунная плита толщиной 0,5 м, длиной 10 м и шириной 4 м лежит на глинистом дне, выдавив из-под себя воду. Глубина водоёма 2,5 м. Какую силу необходимо приложить, чтобы начать подъём плиты?
Решение. Объём плиты V = 0,5 м · 10 м · 4 м = 20 м3.
Её масса m = Vρч = 20 м3 · 7000 кг/м3 = 140 000 кг.
Сила тяжести mg = 1 400 000 Н.
Поскольку под плитой нет воды, сила Архимеда на неё не действует. Вниз на плиту, кроме силы тяжести, действуют сила давления воды на глубине 2,5 – 0,5 = 2 (м) и сила давления атмосферы, которую передаёт вода по закону Паскаля. При нормальном атмосферном давлении общее давление на плиту:
p = pв + pа = 1,2 · 105 Па.
Горизонтальная площадь поверхности плиты
S = 40 м2. Сила давления на плиту F = pS = 4,8 · 106 Н.
Полная сила, прижимающая плиту к грунту:
F = mg + Fа = 1,4 · 106 Н + 4,8 · 106 Н = 6,2 ·106 Н.
Для отрыва от грунта нужна сила F > 6,2 МН.
Источник
Похожие вопросы:
Математика, 08.03.2019 10:00
Цилиндрический сосуд с радиусом основания 50 см наполовину наполнен водой. в сосуд бросили металлический шар радиусом 30 см, который полностью погрузился в воду. на сколько сантиметров поднялся уровень воды в
сосуде
Ответов: 3
Алгебра, 08.03.2019 16:30
Цилиндрический сосуд радиусом основания 50 см наполовину наполнен водой. в сосуд бросили металлический шар радиусом 30 см, который полностью погрузился в воду. на сколько сантиметров поднялся уровень воды в
сосуде?
Ответов: 3
Алгебра, 27.05.2019 05:30
Всосуд имеющий форму правильной треугольной призмы со стороной основания 30 см, налили воду. высота уровня воды равна 120 см. воду перелили в другой сосуд такой же формы, в результате чего высота уровня воды понизилась на 90 см. найдите длину (в см) стороны основания второго сосуда.
Ответов: 1
Алгебра, 27.05.2019 05:30
Всосуд имеющий форму правильной треугольной призмы со стороной основания 30 см, налили воду. высота уровня воды равна 120 см. воду перелили в другой сосуд такой же формы, в результате чего высота уровня воды понизилась на 90 см. найдите длину (в см) стороны основания второго сосуда.
Ответов: 3
Геометрия, 22.06.2019 21:10
Всосуд имеющий форму правильной треугольной призмы со сторонами основания 15 см. налили воду высота воды составила 60 см. воду перелили в другой сосуд такой же формы уровень воды понизился на 45 см. найти сторону основания. сделайте лень самому : d
Ответов: 1
Математика, 01.07.2019 16:30
Всосуд, имеющий форму правильной треугольной призмы со стороной основания 25 см, налили воду. высота уровня воды равна 100 см. воду перелили в другой сосуд такой же формы, в результате чего высота уровня воды понизилась на 75 см. найдите длину (в см) стороны основания второго сосуда.
Ответов: 1
Геометрия, 17.07.2019 04:40
Всосуд, имеющий форму правильной треугольной призмы со стороной основания 25 см, налили воду. высота уровня воды равна 100 см. воду перелили в другой сосуд такой же формы, в результате чего высота уровня воды понизилась на 75 см. найдите длину (в см) стороны основания второго сосуда.
Ответов: 2
Математика, 19.07.2019 06:30
Многоугольник составлен из четырех фигур без наложения друг на друга площади которых равны 7 квадратных сантиметров 12 квадратных сантиметров 32 квадратных сантиметров и 14 квадратных сантиметров чему равна площадь этого многоугольника
Ответов: 2
Математика, 11.08.2019 05:10
Всосуд имеющий форму правильной треугольной призмы со стороной основания 2 см налили воду. уровень воды достигает 75 см. воду переливают в другой такой же сосуд с другой по величине стороной основания и уровень воды достигает вычоты 3см. найдите сторону основания вторго сосуда.
Ответов: 3
Математика, 30.08.2019 19:40
Сосуд в виде прямоугольного параллелепипеда с высотой 20 см и сторонами основания 10 см и 15 см наполнен водой. а)найдите площадь боковой поверхности параллелепипеда. б)сколько литров воды в сосуде в)воду из данного сосуда перелили в сосуд, имеющий форму куба с ребром 20 см. на какой уровень поднялась вода в кубическом сосуде? г)найдите отношение между емкостями сосудов
Ответов: 3
Математика, 01.09.2019 15:00
Решите : объем куба равен 27 кубических сантиметров. найдите площадь его поверхности. ответы: а) 72 квадратных сантиметров б) 54 квадратных сантиметров в) 36 квадратных сантиметров г) 27 квадратных сантиметров запишите ещё и решение!
Ответов: 1
Математика, 11.09.2019 20:20
Два квадратных листа бумаги 9*9 см лежит на столе так, что получается прямоугольник 9*13 см. какая площадь покрыта два стола? а) 45 квадратных сантиметров б) 16 квадратных сантиметров в)117 квадратных сантиметров г)36 квадратных сантиметров
Ответов: 1
У тебя есть свой ответ?
Впрямоугольный сосуд, имеющий площадь основания 20 сантиметров квадратных и содержит воду , бросили…
Отправлено
Вопросы по другим предметам:
Английский язык, 03.09.2019 21:20
Русский язык, 03.09.2019 19:59
Математика, 03.09.2019 21:20
Русский язык, 03.09.2019 19:59
Русский язык, 03.09.2019 21:20
Русский язык, 03.09.2019 19:59
Математика, 03.09.2019 21:20
Английский язык, 03.09.2019 19:59
История, 03.09.2019 21:20
Биология, 03.09.2019 19:59
У тебя есть свой ответ?
Впрямоугольный сосуд, имеющий площадь основания 20 сантиметров квадратных и содержит воду , бросили…
Отправлено
Источник
ÐадаÑа â13 из 45 |
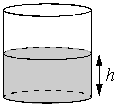Ðода в ÑоÑÑде ÑилиндÑиÑеÑкой ÑоÑÐ¼Ñ Ð½Ð°Ñ
одиÑÑÑ Ð½Ð° ÑÑовне h= 80 Ñм. Ðа каком ÑÑовне окажеÑÑÑ Ð²Ð¾Ð´Ð°, еÑли ÐµÑ Ð¿ÐµÑелиÑÑ Ð² дÑÑгой ÑилиндÑиÑеÑкий ÑоÑÑд, Ñ ÐºÐ¾ÑоÑого ÑадиÑÑ Ð¾ÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð²Ð´Ð²Ð¾Ðµ болÑÑе, Ñем Ñ Ð¿ÐµÑвого? ÐÑÐ²ÐµÑ Ð´Ð°Ð¹Ñе
в ÑанÑимеÑÑаÑ
.
РеÑение задаÑи:
ÐÑи пеÑеливании Ð²Ð¾Ð´Ñ Ð¸Ð· одного ÑоÑÑда в дÑÑгой, обÑем водÑ, еÑÑеÑÑвенно, не менÑеÑÑÑ.
ÐÑÑÑÑ r – ÑадиÑÑ Ð¾ÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð¿ÐµÑвого ÑоÑÑда.
Тогда плоÑÐ°Ð´Ñ Ð¾ÑнованиÑ:
S=πr2
ÐбÑем водÑ:
V=S*h=πr2h
ÐлоÑÐ°Ð´Ñ Ð¾ÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð²ÑоÑого ÑоÑÑда:
S2=πR2=π(2r)2=4πr2 (R – ÑадиÑÑ Ð²ÑоÑого ÑоÑÑда = 2r, по ÑÑловиÑ)
ÐбÑем водÑ:
V2=S2*h2=4πr2h2
Ðак Ð¼Ñ Ñже Ñказали Ñанее обÑем Ð²Ð¾Ð´Ñ Ð½Ðµ менÑеÑÑÑ, Ñ.е. V=V2, полÑÑаем:
πr2h=4πr2h2 |:πr2
h=4h2
80=4h2
h2=80/4=20
ÐÑвеÑ: 20
ÐоделиÑеÑÑ ÑеÑением
ÐÑиÑоединÑйÑеÑÑ Ðº нам…
ÐÑ Ð¼Ð¾Ð¶ÐµÑе поблагодаÑиÑÑ Ð°Ð²ÑоÑа, напиÑаÑÑ Ñвои пÑеÑензии или пÑÐµÐ´Ð»Ð¾Ð¶ÐµÐ½Ð¸Ñ Ð½Ð°
ÑÑÑаниÑе ‘ÐÑо нађ
ÐÑÑгие задаÑи из ÑÑого Ñаздела

ÐадаÑа â006B44
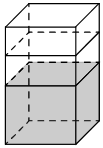Рбак, имеÑÑий ÑоÑÐ¼Ñ Ð¿ÑÑмой пÑизмÑ, налиÑо 5 л водÑ. ÐоÑле полного погÑÑÐ¶ÐµÐ½Ð¸Ñ Ð² Ð²Ð¾Ð´Ñ Ð´ÐµÑали ÑÑÐ¾Ð²ÐµÐ½Ñ Ð²Ð¾Ð´Ñ
в баке поднÑлÑÑ Ð² 1,4 Ñаза. ÐайдиÑе обÑÑм деÑали. ÐÑÐ²ÐµÑ Ð´Ð°Ð¹Ñе в кÑбиÑеÑкиÑ
ÑанÑимеÑÑаÑ
, знаÑ, ÑÑо в одном лиÑÑе
1000 кÑбиÑеÑкиÑ
ÑанÑимеÑÑов.

ÐадаÑа â482E4E
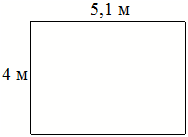Ðа плане Ñказано, ÑÑо пÑÑмоÑголÑÐ½Ð°Ñ ÐºÐ¾Ð¼Ð½Ð°Ñа Ð¸Ð¼ÐµÐµÑ Ð¿Ð»Ð¾ÑÐ°Ð´Ñ 20,1 кв. м. ТоÑнÑе измеÑÐµÐ½Ð¸Ñ Ð¿Ð¾ÐºÐ°Ð·Ð°Ð»Ð¸, ÑÑо ÑиÑина комнаÑÑ Ñавна 4 м,
а длина 5,1 м. Ðа ÑколÑко квадÑаÑнÑÑ
меÑÑов плоÑÐ°Ð´Ñ ÐºÐ¾Ð¼Ð½Ð°ÑÑ Ð¾ÑлиÑаеÑÑÑ Ð¾Ñ Ð¿Ð»Ð¾Ñади, Ñказанной на плане?

ÐадаÑа â4E4948
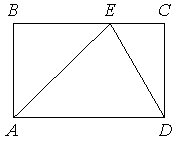Ðа ÑÑоÑоне BC пÑÑмоÑголÑника ABCD, Ñ ÐºÐ¾ÑоÑого AB=12 и AD=17, оÑмеÑена ÑоÑка E Ñак, ÑÑо ÑÑеÑголÑник ABE ÑавнобедÑеннÑй. ÐайдиÑе ED.

ÐадаÑа â0EF144
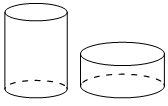ÐÐ°Ð½Ñ Ð´Ð²Ð° ÑилиндÑа. РадиÑÑ Ð¾ÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð¸ вÑÑоÑа пеÑвого ÑилиндÑа ÑÐ°Ð²Ð½Ñ ÑооÑвеÑÑÑвенно 2 и 6,
а вÑоÑого â 6 и 4. Ðо ÑколÑко Ñаз обÑÑм вÑоÑого ÑилиндÑа болÑÑе обÑÑма пеÑвого?

ÐадаÑа âC52A4F
Ðакой наименÑÑий Ñгол (в гÑадÑÑаÑ
) обÑазÑÑÑ Ð¼Ð¸Ð½ÑÑнаÑ
и ÑаÑÐ¾Ð²Ð°Ñ ÑÑÑелки ÑаÑов в 17:00?
Источник
504. Сосуд с жидкостью наклонили (рис. 131). Одинаковое ли давление оказывает после этого жид¬кость на боковые стенки А и В в точках, лежащих на одном горизонтальном уровне?
Жидкость оказывает одинаковое давление на одном горизонтальном уровне везде, в том числе и на стенках А и В (см. рис. 131).
505. Сосуд с водой имеет форму, изображенную на рисунке 132. Одинаково ли давление воды на боковые стенки сосуда на уровне аб?
На уровне ab давление воды на боковые стенки одно и то же (см. рис. 132).
506. Цилиндрические сосуды уравновешены на весах (рис. 133). Нарушится ли равновесие весов, если в них налить воды столько, что поверхность ее установится на одинаковом уровне от дна сосудов? Одинаково ли будет давление на дно сосудов?
Равновесие весов нарушается, так как в разных сосудах различная масса воды. Давление на дно сосуда будет одинаковым, так как высота столба воды в обоих сосудах одна и та же (см. рис. 133)
507. Цилиндрические сосуды уравновешены на весах (см. рис. 133). Мальчик налил в оба сосуда воду одинаковой массы. Нарушилось ли равновесие весов? Одинаково ли будет давление воды на дно сосудов?
Равновесие весов не нарушилось. Давление воды на дно сосуда будет различным, так как уровень налитой воды будет различным (см. рис. 133).
508. В цилиндрический сосуд, частично заполненный водой, опустили деревянный брусок. Изменилось ли давление воды на дно сосуда?
Давление воды на дно увеличилось, так как при опускании в воду деревянного бруска ее уровень поднялся.
509. В трех сосудах с одинаковой площадью дна налита вода до одного уровня (рис. 134). В каком сосуде налито больше воды? Одинаково ли давление на дно в этих сосудах? Почему?
Воды налито больше в крайнем левом сосуде. Давление на дно будет одинаковым во всех трех сосудах, так как везде вода налита до одного уровня (см. рис. 134).
510. Уровень воды в сосудах одинаковый (рис. 135). Будет ли переливаться вода из одного сосуда в другой, если открыть кран?
При открывании крана вода из одного сосуда в другой переливаться не будет, так как уровень воды в сосудах будет одинаковый, а следовательно давление воды на любом уровне так же одинаково (см. рис. 135).
511. Уровень жидкостей в сосудах (см. рис. 135) одинаковый. В левом налита вода, в правом — керосин. Одинаковы ли давления на дно? Одинаковы ли давления на кран? Будет ли переливаться жидкость из одного сосуда в другой, если открыть кран?
Давление воды на дно и на кран больше, чем давление керосина. Объясняется это тем, что плотность воды больше плотности керосина. Если кран открыть, то вследствие разности давлений вода потечет в сосуд с керосином (см. рис. 135).
512. В левой части сосуда над жидкостью находится воздух (рис. 136). Какую высоту столба жидкости следует учитывать при расчете давления на дно сосуда: высоту Н или высоту H1? Ответ объясните.
513. В полиэтиленовый мешок налита вода (рис. 137). Что показывают динамометры: давление или силы, действующие на столики динамометров? Стрелка правого динамометра закрыта листом бумаги. Каково показание правого динамометра? Будут ли изменяться показания динамометров, если воду в мешок доливать (выливать)? Ответы обоснуйте.
Динамометры показывают силы давления жидкости на боковые стенки сосуда с водой. Показания их одинаковы и равны 70Н. Если воду в мешок доливать, то показания динамометров увеличатся, а если воду выливать, то уменьшатся, т.к. увеличится либо уменьшится давление столба жидкости (см. рис.137).
514. Одинаково ли давление воды на дно сосудов (рис. 138)? Чему равно это давление? Изменится ли давление, если воду заменить керосином? Чему оно будет равно в этом случае?
515. Высота столба воды в стакане 8 см. Какое давление на дно стакана оказывает вода? Какое давление оказывала бы ртуть, налитая до того же уровня?
516. Какое давление на дно сосуда оказывает слой керосина высотой 0,5 м?
517. В цилиндрический сосуд налиты ртуть, вода и керосин. Определите общее давление, которое оказывают жидкости на дно сосуда, если объемы всех жидкостей равны, а верхний уровень керосина находится на высоте 12 см от дна сосуда.
518. Сосуды с водой имеют равные площади дна (рис. 139). В каком из них избыточное давление воды на дно (без учета атмосферного давления) больше и во сколько раз?
519. Водолаз в жестком скафандре может погружаться в море на глубину 250 м, искусный ныряльщик — на глубину 20 м. На сколько и во сколько раз отличаются давления воды на этих глубинах?
520. Рассчитайте давление воды: а) на самой большой глубине Тихого океана — 11 035 м; б) на наибольшей глубине Азовского моря — 14 м (плотность воды в нем принять равной 1020 кг/м3).
521. Определите по графику (рис. 140) глубину погружения тела в озеро, соответствующую давлению воды 100, 300 и 500 кПа.
10 м; 30 м; 50 м (рис. 140).
522. Аквариум наполнен доверху водой. С какой силой давит вода на стенку аквариума длиной 50 см и высотой 30 см?
523. В аквариум высотой 32 см, длиной 50 см и шириной 20 см налита вода, уровень которой ниже края на 2 см. Рассчитайте: а) давление воды на дно; б) вес воды; в) силу, с которой вода действует на стенку шириной 20 см.
524. Ширина шлюза 10 м. Шлюз заполнен водой на глубину 5 м. С какой силой давит вода на ворота шлюза?
525. В цистерне, заполненной нефтью, на глубине 3 м имеется кран, площадь отверстия которого 30 см2. С какой силой давит нефть на кран?
526. Прямоугольный сосуд вместимостью 2 л наполовину наполнен водой, а наполовину керосином, а) Каково давление жидкостей на дно сосуда? б) Чему равен вес жидкостей в сосуде? Дно сосуда имеет форму квадрата сo стороной 10 см.
527. Определите силу, с которой действует керосин на квадратную пробку площадью поперечного сечения 16 см2, если расстояние от пробей до уровня керосина в сосуде равно 400 мм (рис. 141).
528. Какую силу испытывает каждый квадратный метр площади поверхности водолазного костюма при погружении в морскую воду на глубину 10 м?
529. Плоскодонная баржа получила пробоину в дне площадью 200 см2. С какой силой нужно давить на пластырь, которым закрывают отверстие, чтобы сдержать напор воды на глубине 1,8 м? (Вес пластыря не учитывать.)
530. Определите высоту уровня воды в водонапорной башне, если манометр, установленный у ее основания, показывает давление 220000 Па.
531. На какой глубине давление воды в море равно 412 кПа?
532. Напор воды в водокачке создается насосом. Определите на какую высоту поднимается вода, если давление, созданное насосом, равно 400 кПа?
533. Брусок размером 0,5×0,4×0,1 м находится в баке с водой на глубине 0,6 м (рис. 142). Вычислите: а) с какой силой вода давит на верхнюю грань бруска; б) на нижнюю грань бруска; в) сколько весит вода, вытесненная бруском.
534. Произведите расчет, взяв данные предыдущей задачи, предполагая, что воду заменили керосином.
535. Используя результаты двух предыдущих задач, вычислите, на сколько сила, действующая на тело снизу, больше силы, действующей на тело сверху: а) в воде; б) в керосине. Сравните полученные результаты с весом вытесненной воды и с весом вытесненного керосина.
536. Один из кофейников, изображенных на рисунке 143, вмещает больше жидкости, чем другой. Укажите какой и объясните.
Правый кофейник вмещает больше жидкости, чем левый, гак как у него кончик носика находится выше.
537. Точкой А обозначен уровень воды в левом колене трубки (рис. 144). Сделайте рисунок и на нем отметьте точкой В уровень воды в правом колене трубки.
538. В сообщающиеся сосуды налита вода. Что произойдет и почему, если в левый сосуд долить немного воды (рис. 145); в средний сосуд долить воды (рис. 146)?
Уровень воды увеличится во всех сосудах на одинаковую высоту. Таким образом, уровни снова выравнятся (рис. 145, 146).
539. Справедлив ли закон сообщающихся сосудов в условиях невесомости? Объясните почему.
Закон сообщающихся сосудов в условиях невесомости не действует, так как жидкости в состоянии невесомости не обладают весом и потому не оказывают давления на дно сосудов.
540. Как при помощи сообщающихся сосудов проверить, горизонтально ли нанесена филенка (линия, отделяющая окраску панели от верхней части стены)?
Нужно взять длинную тонкую резиновую трубку, вставить стеклянные трубки на концах, залить эту систему водой, а концы стеклянных трубок подвести к филенке. Используя свойство сообщающихся сосудов, пройтись с одной из стеклянных трубок вдоль стены.
541. Объясните действие фонтана (рис. 147).
Действие фонтана объясняется тем, что давление жидкости в верхнем конце правой трубки будет больше атмосферного, так как уровень воды в этой трубке меньше уровня воды в левой трубке.
542. В левом колене сообщающихся сосудов налита вода, в правом — керосин (рис. 148). Высота столба керосина 20 см. Рассчитайте, на сколько уровень воды в левом колене ниже верхнего уровня керосина.
543. В сообщающихся сосудах находятся ртуть и вода (рис. 149). Высота столба воды 68 см. Какой высоты столб керосина следует налить в левое колено, чтобы ртуть установилась на одинаковом уровне?
544. В сообщающихся сосудах находилась ртуть. Когда в правую трубку налили слой керосина высотой 34 см, то уровень ртути в левой трубке поднялся на 2 см. Какой высоты следует налить слой воды в левую трубку, чтобы ртуть в трубках установилась на одинаковом уровне (рис. 149)?
545. В сообщающихся сосудах находятся ртуть, вода и керосин (рис. 150). Какова высота слоя керосина, если высота столба воды равна 20 см и уровень ртути в правом колене ниже, чем в левом, на 0,5 см?
Источник