В сообщающиеся сосуды налиты две разнородные жидкости
Часть А содержит 30 заданий (А1 – А30). К каждому заданию дается 4 варианта ответа, из которых правильный только один.
Внимательно прочитайте каждое задание и предлагаемые варианты ответа. Отвечайте только после того, как вы поняли вопрос и проанализировали все варианты ответа.
Выбрав нужный вариант ответа под номером выполняемого вами задания (А 1–А 30), кликните мышкой в кружочке, соответствующем выбранному вами ответу.
Выполняйте задания в том порядке, в котором они даны. Если какое-то задание вызывает у вас затруднение, пропустите его. К пропущенным заданиям можно будет вернуться, если у вас останется время.
За выполнение каждого задания дается один балл. Баллы, полученные вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Желаем успеха!
Здесь приведены справочные данные, которые могут понадобиться вам при выполнении работы.
Полный перечень вопросов, которые могут контролироваться на едином государственном экзамене 2010 года, приведен в кодификаторе, помещённом на сайтах www.ege.edu.ru и www.fipi.ru.
A1. Действие гидравлического пресса основано на
законе Архимеда
законе Паскаля
законе сохранения импульса
законе Кулона
A2. С помощью гидравлического пресса можно получить выигрыш
в силе
в работе
в скорости
в давлении
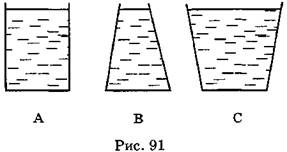 A3. На рис. 91 изображены три сосуда разной формы с одинаковой площадью основания, в которые налита одинаковая жидкость. Верхний уровень жидкости в сосудах тоже одинаков. Сила давления на дно больше веса жидкости в сосуде
A3. На рис. 91 изображены три сосуда разной формы с одинаковой площадью основания, в которые налита одинаковая жидкость. Верхний уровень жидкости в сосудах тоже одинаков. Сила давления на дно больше веса жидкости в сосуде
A
B
C
одинаковы во всех сосудах
A4. Единица давления в СИ может быть выражена через основные единицы СИ следующим образом:
кг•м•с-2
кг•м-1•с2
кг•м-1•с-2
кг•м2•с-2
A5. Верным является утверждение, что давление
векторная величина, равная произведению силы давления на ее плечо
скалярная величина, равная отношению силы давления к массе тела
векторная величина, равная произведению массы и скорости тела
скалярная величина, равная отношению силы давления к площади опоры
A6. В сообщающиеся сосуды налиты две разнородные жидкости (рис. 92). Плотность жидкости в левом колене равна 600 кг/м3. Плотность жидкости в правом колене равна
400 кг/м3
700 кг/м3
900 кг/м3
1000 кг/м3
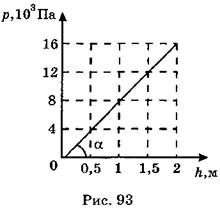
A7. На рис. 93 изображен график зависимости давления жидкости p от ее глубины h. Плотность этой жидкости равна
600 кг/м3
800 кг/м3
1000 кг/м3
1200 кг/м3
A8. Куб с длиной ребра 20 см плавает в воде, наполовину погруженным в нее. Плотность воды 1000 кг/м3. На куб действует выталкивающая сила, равная
40 Н
160 Н
80 Н
100 Н
A9. Труба имеет переменное сечение. Радиус ее широкой части 10 см, скорость воды в ней 4 м/с. Чему равна скорость воды в узкой части трубы радиусом 4 см?
25 м/с
40 м/с
20 м/с
16 м/с
A10. Вес тела в воздухе 400 Н, а в воде 320 Н. Плотность воды 1000 кг/м3. Объем тела равен
400 см3
4000 см3
8000 см3
7200 см3
A11. Какой из графиков (рис. 94) правильно показывает зависимость концентрации молекул от объема газа при неизменном общем числе молекул?
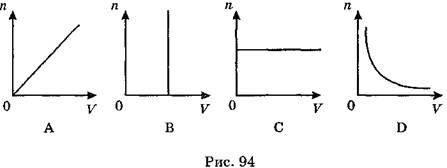
A
B
C
D
A12. По мере сжатия газа
увеличиваются силы отталкивания между молекулами, а силы их взаимного притяжения уменьшаются
увеличиваются и силы отталкивания, и силы притяжения молекул друг к другу
увеличиваются силы притяжения молекул друг к другу, а силы их взаимного отталкивания уменьшаются
уменьшаются силы взаимного притяжения молекул, а силы их взаимного отталкивания остаются неизменными
A13. В баллон емкостью 10 л впустили 5 л кислорода, 4 л азота и 8 л водорода. Объем смеси этих газов стал равен
12 л
10 л
17 л
8 л
A14. Близким к идеальному является газ, находящийся
под высоким давлением и при низкой температуре
под низким давлением и при низкой температуре
под низким давлением и при высокой температуре
под высоким давлением и при высокой температуре
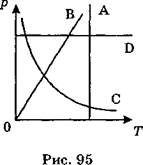 A15. На рис. 95 изохорному процессу соответствует график
A15. На рис. 95 изохорному процессу соответствует график
A16. Под поршнем массой 2 кг с площадью основания 5 см2 находится газ. Поршень находится в состоянии равновесия. Атмосферное давление нормальное (105 Па). Чему равно давление газа под поршнем?
2•105 Па
0,8•105 Па
1•105 Па
1,4•105 Па
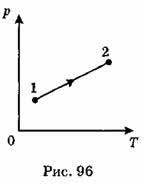 A17. На рис. 96 показана зависимость давления данной массы идеального газа от его температуры. В этом процессе объем газа
A17. На рис. 96 показана зависимость давления данной массы идеального газа от его температуры. В этом процессе объем газа
увеличивался
уменьшался
не изменялся
нет однозначного ответа
А18. Температура газа 27 °С. Постоянная Больцмана 1,38•10-23Дж/К. Средняя кинетическая энергия молекул газа примерно равна
6,2•10-21Дж
3,7•10-22Дж
5,6•10-22Дж
2,6•10-23Дж
A19. В закрытом сосуде находится газ под давлением 200 кПа. Каким станет давление газа, если температуру повысить на 30% ?
170 кПа
260 кПа
320 кПа
400 кПа
A20. Относительная влажность воздуха 60%, давление насыщенного пара в нем при некоторой температуре равно 2,2 кПа. Чему равно парциальное давление пара при этой же температуре?
0,9 кПа
0,7 кПа
1,8 кПа
1,3 кПа
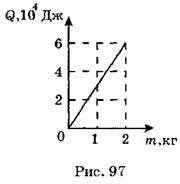 A21. На рис. 97 показан график зависимости количества теплоты, необходимого для нагревания на 10 °С некоторого вещества, от его массы. Удельная теплоемкость этого вещества равна
A21. На рис. 97 показан график зависимости количества теплоты, необходимого для нагревания на 10 °С некоторого вещества, от его массы. Удельная теплоемкость этого вещества равна
600 Дж/(кг•К)
1200 Дж/(кг•К)
3000 Дж/(кг•К)
4200 Дж/(кг•К)
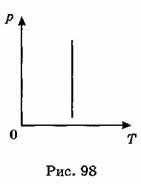
A22. На рис. 98 изображен график зависимости давления газа от его температуры. Газ получает от нагревателя количество теплоты 300 Дж. При этом
изменение его внутренней энергии равно нулю, а совершенная газом работа равна 300 Дж
изменение его внутренней энергии равно 300 Дж, а работы газ не совершает
внутренняя энергия газа уменьшается на 300 Дж, и газ совершает работу 300 Дж
внутренняя энергия газа увеличивается на 150 Дж, и газ совершает работу 150 Дж
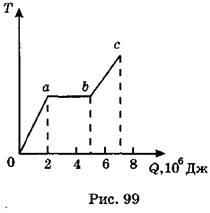
A23. На рис. 99 изображен график изменения температуры жидкости массой 1 кг в зависимости от переданного ей количества теплоты. Удельная теплота парообразования этой жидкости равна
5•106Дж/кг
7•106 Дж/кг
2•106 Дж/кг
3•106 Дж/кг
A24. Газ сжали, совершив 300 Дж работы, и он выделил во внешнюю среду 500 Дж теплоты. При этом его внутренняя энергия
увеличилась на 800 Дж
уменьшалась на 200 Дж
уменьшилась на 100 Дж
увеличилась на 400 Дж
A25. Под давлением 100 кПа данная масса газа изобарно расширилась, увеличив объем с 3 л до 9 л. При этом внутренняя энергия газа
увеличилась на 1800 Дж
увеличилась на 900 Дж
уменьшилась на 600 Дж
уменьшилась на 300 Дж
A26. Тело массой 5 кг упало с высоты 4 м. При этом 40% его механической энергии пошла на нагревание. Количество теплоты, полученное телом при нагревании равно
200 Дж
100 Дж
60 Дж
80 Дж
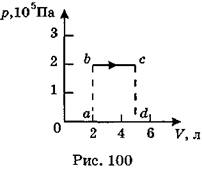 A27. На рис. 100 изображен график изобарного расширения газа в координатах р – V, вследствие передачи ему извне 900 Дж теплоты. При этом внутренняя энергия газа
A27. На рис. 100 изображен график изобарного расширения газа в координатах р – V, вследствие передачи ему извне 900 Дж теплоты. При этом внутренняя энергия газа
увеличилась на 300 Дж
увеличилась на 500 Дж
уменьшилась на 400 Дж
уменьшилась на 100 Дж
A28. При изотермическом сжатии идеального газа его внутренняя энергия
увеличивается
не изменяется
уменьшается
может увеличиваться или уменьшаться в зависимости от скорости сжатия
A29. Двигатель внутреннего сгорания автомобиля имеет наибольший КПД
летом
осенью
зимой
весной
A30. КПД идеального теплового двигателя 60 % , температура внешней среды 27 °С. Температура его нагревателя равна
350 К
750 К
1050 К
3000 К
Источник

Сообщающиеся сосуды – это сосуды, соединенные между собой ниже уровня жидкости в каждом из сосудов. Таким образом жидкость может перемещаться из одного сосуда в другой.
Перед тем как понять принцип действия сообщающихся сосудов и варианты их использования необходимо определиться в понятиях, а точнее разобраться с основным уравнением гидростатики.
Итак, сообщающиеся сосуды имеют одно общее дно и закон о сообщающихся сосудах гласит:
Какую бы форму не имели такие сосуды, на поверхности однородных жидкостей в состоянии покоя на одном уровне действует одинаковое давление.
Для иллюстрации этого закона и возможностей его применения начнем с рассмотрения основного уравнения гидростатики.
Основное уравнение гидростатики

P = P1 + ρgh
где P1 – это среднее давление на верхний торец призмы,
P – давление на нижний торец,
g – ускорение свободного падения,
h – глубина погружения призмы под свободной поверхностью жидкости.
ρgh – сила тяжести (вес призмы).
Звучит уравнение так:
Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.
Из написанного выше уравнения следует, что если давление, например в верхней точке изменится на какую-то величину ΔР, то на такую же величину изменится давление в любой другой точке жидкости
Доказательство закона сообщающихся сосудов
Возвращаемся к разговору про сообщающиеся сосуды.

Предположим, что имеются два сообщающихся сосуда А и В, заполненные различными жидкостями с плотностями ρ1 и ρ2. Будем считать, что в общем случае сосуды закрыты и давления на свободных поверхностях жидкости в них соответственно равны P1 и P2.
Пусть поверхностью раздела жидкостей будет поверхность ab в сосуде А и слой жидкости в этом сосуде равен h1. Определим в заданных условиях уровень воды в сообщающихся сосудах – начнем с сосуда В.
Гидростатическое давление в плоскости ab, в соответствии с уравнение гидростатики
P = P1 + ρgh1
если определять его, исходя из известного давления P1 на поверхность жидкости в сосуде А.
Это давление можно определить следующим образом
P = P2 + ρgh2
где h2 – искомая глубина нагружения поверхности ab под уровнем жидкости в сосуде В. Отсюда выводим условие для определения величины h2
P1 + ρ1gh1 = P2 + ρ2gh2
В частном случае, когда сосуды открыты (двление на свободной поверхности равно атмосферному), а следовательно P1 = P2 = Pатм , имеем
ρ1h1 = ρ2h2
или
ρ1 / ρ2 = h2 / h1
т.е. закон сообщающихся сосудов состоит в следующем.
В сообщающихся сосудах при одинаковом давлении на свободных поверхностях высоты жидкостей, отсчитываемые от поверхности раздела, обратно пропорциональны плотностям жидкостей.
Свойства сообщающихся сосудов

Если уровень в сосудах одинаковый, то жидкость одинаково давит на стенки обоих сосудов. А можно ли изменить уровень жидкости в одном из сосудов.
Можно. С помощью перегородки. Перегородка, установленная между сосудами перекроет сообщение. Далее доливая жидкость в один из сосудов мы создаем так называемый подпор – давление столба жидкости.
Если затем убрать перегородку, то жидкость начнет перетекать в тот сосуд где её уровень ниже до тех пор пока высота жидкости в обоих сосудах не станет одинаковой.
В быту этот принцип используется например в водонапорной башне. Наполняя водой высокую башню в ней создают подпор. Затем открывают вентили, расположенные на нижнем этаже и вода устремляется по трубопроводам в каждый подключенный к водоснабжению дом.
Приборы основанные на законе сообщающихся сосудов

На принципе сообщающихся сосудов основано устройство очень простого прибора для определения плотности жидкости. Этот прибор представляет собой два сообщающихся сосуда – две вертикальные стеклянные трубки А и В, соединенные между собой изогнутым коленом С. Одна из вертикальных трубок заполняется исследуемой жидкостью, а другая жидкостью известной плотности ρ1 (например водой), причем в таких количествах, чтобы уровни жидкости в среднем колене находились на одной и той же отметке прибора 0.
Затем измеряют высоты стояния жидкостей в трубках над этой отметкой h1 и h2. И имея ввиду, что эти высоты обратно пропорциональны плотностям легко находят плотность исследуемой жидкости.

В случае, когда оба сосуде заполнены одной и той же жидкостью – высоты, на которые поднимется жидкость в сообщающихся сосудах, будут одинаковы. На этом принципе основано устройство так называемого водометного стекла А. Его применяют для определения уровня жидкости в закрытых сосудах, например резервуарах, паровых котлах и т.д.
Принцип сообщающихся сосудов заложен в основе ряда других приборов, предназначенных для измерения давления.
Применение сообщающихся сосудов

Простейшим прибором жидкостного типа является пьезометр, измеряющий давление в жидкости высотой столба той же жидкости.
Пьезометр представляет собой стеклянную трубку небольшого диаметра (обычно не более 5 мм), открытую с одного конца и вторым концом присоединяемую к сосуду, в котором измеряется давление.
Высота поднятия жидкости в пьезометрической трубке – так называемая пьезометрическая высота – характеризует избыточное давление в сосуде и может служить мерой для определения его величины.
Пьезометр – очень чувствительный и точный прибор, но он удобен только для измерения небольших давлений. При больших давлениях трубка пьезометра получается очень длинной, что усложняет измерения.
В этом случае используют жидкостные манометры, в которых давление уравновешивается не жидкостью, которой может быть вода в сообщающихся сосудах, а жидкостью большей плотности. Обычно такой жидкостью выступает ртуть.

Так как плотность ртути в 13,6 раз больше плотности воды и при измерении одних и тех же давлений трубка ртутного манометра оказывается значительно короче пьезометрической трубки и сам прибор получается компактнее.
В случае если необходимо измерить не давление в сосуде, а разность давлений в двух сосудах или, например, в двух точках жидкости в одном и том же сосуде применяют дифференциальные манометры.
Сообщающиеся сосуды находят применение в водяных и ртутных приборах жидкостного типа, но ограничиваются областью сравнительно небольших давлений – в основном они применяются в лабораториях, где ценятся благодаря своей простоте и высокой точности.

Когда необходимо измерить большое давление применяются приборы основанные на механических принципах. Наиболее распространенный из них – пружинный манометр. Под действием давления пружина манометра частично распрямляется и посредством зубчатого механизма приводит в движение стрелку, по отклонению которой на циферблате показана величина давления.
Видео по теме
Ещё одним устройством использующим принцип сообщающихся сосудов хорошо знакомым автолюбителем является гидравлический пресс(домкрат). Конструктивно он состоит из двух цилиндров: одного большого, другого маленького. При воздействии на поршень малого цилиндра на большой передается усилие во столько раз большего давления во сколько площадь большого поршня больше площади малого.
Вместе со статьей “Закон сообщающихся сосудов и его применение.” читают:
Источник
Статьи
Основное общее образование
Линия УМК А. В. Перышкина. Физика (7-9)
Физика
Все мы ежедневно пользуемся сообщающимися сосудами – это чайник, лейка, в общем, это любая система ёмкостей, в которых жидкость, к примеру, вода, может свободно перетекать из одной ёмкости в другую. В чайнике, например, такими ёмкостями являются корпус и носик или корпус чайника и специальная ёмкость для определения уровня воды в нём. Что особенного в сообщающихся сосудах? Каким свойством или свойствами они обладают? Чем заслуживают наше внимание?
26 апреля 2019
Закон сообщающихся сосудов
Сосуды соединенные между собой, жидкость в которых может свободно перетекать, имеющие общее дно, называются сообщающимися. В соответствии с законом Паскаля, жидкость передаёт оказываемое на неё давление во всех направлениях одинаково. В открытых сосудах, атмосферное давление над каждым из них одинаково, значит, и давление жидкости на стенки сосудов будет одинаковым на любом уровне. Так как давление жидкости прямо пропорционально её плотности и глубине, в случае одинаковой жидкости в сообщающихся сосудах на одинаковой глубине будет одинаковое давление, что и объясняет выравнивание уровней жидкости в них. В случае разных жидкостей, чтобы на одинаковой глубине было одинаковое давление, жидкость с меньшей плотностью должна иметь больший уровень в сравнении с жидкостью большей плотности. Т.е.
ρ1 / ρ2 = h2 / h1
Физика. 7 класс. Учебник
Учебник соответствует Федеральному государственному образовательному стандарту основного общего образования. Большое количество красочных иллюстраций, разнообразные вопросы и задания, а также дополнительные сведения и любопытные факты способствуют эффективному усвоению учебного материала.
Купить
Свойство сообщающихся сосудов
Возьмем несколько различных по размеру и форме открытых сосудов, проделаем в каждом из них отверстие и соединим отверстия в сосудах трубками, чтобы жидкость, которую мы будем наливать в один из них, могла свободно перетекать из одного сосуда в другой. Для большего эффекта, пожмем трубки, которые их соединяют и наполним один из сообщающихся сосудов водой. Теперь откроем трубки и увидим, что когда жидкость перестанет перетекать, то, вне зависимости от формы и размера сосудов, уровни жидкости в каждом будут совершенно одинаковыми. Или проведём иной опыт – возьмём пластиковую бутыль и срежем донышко, а крышку плотно прикрутим, проделаем в ней небольшое отверстие и вставим в него небольшой шланг, место соединения шланга и крышки бутыли сделаем герметичным с помощью пластилина. Теперь закрепим бутыль вверх дном, а шланг расположим параллельно бутыли открытым концом чуть выше её срезанного дна. Заполним бутыль жидкостью, например, подкрашенной водой. И вновь мы увидим, что вне зависимости от высоты сообщающихся сосудов, уровень воды в бутыли будет точно таким же, как и уровень воды в шланге. В этом и заключается первое и основное свойство сообщающихся сосудов: в открытых сообщающихся сосудах уровни одинаковой жидкости будут одинаковыми. Это замечательное свойство нашло широкое применение в практике, но об этом поговорим чуть позже. А теперь возьмём U-образную стеклянную трубку. Это тоже сообщающиеся сосуды, их, в данном случае, называют коленами трубки. В правое колено нальём воду и она, конечно же, перетечёт в левое колено так, что уровни воды в обоих коленах будут одинаковыми – мы уже знаем, что так и должно быть, хоть пока что и не знаем, почему. А теперь в левое колено, очень аккуратно, чтобы жидкости не смешивались, нальём керосин или подкрашенный спирт. И мы увидим, что теперь верхние уровни каждой жидкости в коленах будут отличаться. Уровень спирта или керосина будет выше уровня воды. Заглянем заодно в таблицу плотности жидкостей и увидим, что плотность керосина или спирта меньше плотности воды, а уровень, наоборот, выше. Из этого эксперимента можно сделать вывод – если в открытых сообщающихся сосудах налиты две разные жидкости, то уровень будет выше у той, чья плотность меньше. Иными словами, плотности жидкостей и их уровни будут обратно пропорциональными. Настала пора объяснить, почему так получается.
Читайте также:
Проекты на уроках физики: плюсы и минусы
Что такое радуга?
Почему море соленое?
Почему небо голубого цвета?
Применение на практике
Благодаря своим свойствам, сообщающиеся сосуды нашли широкое применение в различных технических и бытовых устройствах. Перечислим некоторые из них:
- измерители плотности,
- жидкостные манометры,
- определители уровня жидкости (водомерное стекло, к примеру),
- домкраты,
- гидравлические прессы,
- шлюзы,
- фонтаны,
- водопроводные башни и т.д.
Свойство сообщающихся сосудов реализуется не только в физике. Такая известная поговорка «Если где-то прибыло, значит где-то убыло» фактически напрямую связана со свойством сообщающихся сосудов и означает, что в окружающем нас мире всё взаимосвязано, а значит – стремится к равновесию. Когда человек смещает это равновесие в одну сторону, это немедленно сказывается в чём-то другом. Над этим стоит задуматься, не так ли?
Материал по физике на тему «Сообщающиеся сосуды» для 7 класса.
Методические советы учителям
- При изучении этой темы обязательно необходима демонстрация. Описанные в статье эксперименты обязательно нужно показать детям в живом исполнении.
- Желательно продемонстрировать принцип действия фонтана (это также довольно не сложно сделать своими руками).
- Обратите внимание учащихся на формулу для двух жидкостей – это обратная пропорция. На нескольких примерах поясните смысл обратной пропорциональности.
- Рассмотрите ситуацию с тремя жидкостями (решите соответствующую задачу).
- А вот действие шлюзов лучше всего продемонстрировать с помощью видео.
#ADVERTISING_INSERT#
Источник
