В сообщающиеся сосуды одинакового сечения налита вода
Опубликовано ср, 07/17/2019 – 14:51 пользователем fizportal.ru



ГИДРОСТАТИКА. Сообщающиеся сосуды. Гидравлический пресс. Тема 12-3
12.38. В сосуд с водой вставлена трубка сечением 2 см2. В трубку налили масло массой 72 г. Плотность масла 900 кг/м3. Найдите разность (в см) между верхними уровнями масла и воды.
12.39. В сообщающиеся сосуды с ртутью долили: в один сосуд столб масла высотой 30 см, в другой сосуд столб воды высотой 20,2 см. Определите разность уровней (в мм) ртути в сосудах. Плотность ртути 13600 кг/м3, масла 900 кг/м3.
12.40. В сообщающихся сосудах находится ртуть. Площадь сечения одного сосуда в 2 раза больше, чем другого. В узкий сосуд наливают столб воды высотой 1,02 м. На сколько миллиметров поднимется ртуть в широком сосуде? Плотность ртути равна 13600 кг/м3.
12.41. К малому поршню гидравлического пресса приложена сила 10 Н, под действием которой за один ход он опускается на 25 см, вследствие чего большой поршень поднимается на 5 мм. Какая сила давления передается при этом на большой поршень?
12.42. При подъеме груза массой 2000 кг с помощью гидравлического пресса была совершена работа 40 Дж. При этом малый поршень сделал 10 ходов, перемещаясь за один ход на 10 см. Во сколько раз площадь большого поршня больше площади малого?
12.43. В сообщающиеся сосуды налита ртуть. В один из сосудов добавили керосин, высота столба которого 27,2 см. На сколько миллиметров уровень ртути в этом сосуде будет ниже, чем в другом? Плотность ртути 13600 кг/м3, плотность керосина 800 кг/м3.
12.44. В сообщающиеся сосуды налита ртуть. В один сосуд добавили воду, высота столба которой 4 см. Какой высоты (в см) должен быть столб некоторой жидкости в другом сосуде, чтобы уровень ртути в обоих сосудах был одинаков, если плотность жидкости в 1,25 раза меньше плотности воды?
12.45. В сообщающиеся сосуды одинакового сечения налита вода. В один из сосудов поверх воды долили столб масла высотой 40 см. На сколько сантиметров изменится уровень воды в другом сосуде? Плотность масла 800 кг/м3.
12.46. В сообщающихся сосудах находится ртуть. Площадь сечения одного сосуда в два раза больше площади другого. Широкий сосуд доливают водой до края. На сколько сантиметров поднимется уровень ртути в другом сосуде? Первоначально уровень ртути был расположен на 39,8 см ниже верхнего края сосуда. Плотность ртути в 13,6 раз больше плотности воды.
12.47. В сообщающихся сосудах одинакового сечения 20 см2 находится вода, закрытая легкими поршнями. На один из поршней помещают груз массой 160 г. На сколько сантиметров поднимется уровень воды в другом сосуде?
12.48. В сообщающихся сосудах площадью сечения 100 см2 находится ртуть. В один из сосудов наливают воду массой 2 кг и опускают в нее деревянный брусок массой 0,72 кг. На сколько миллиметров поднимется ртуть в другом сосуде? Плотность ртути 13600 кг/м3.
12.49. Чему равен КПД двигателя, приводящий в действие гидравлический пресс, у которого отношение площадей поршней равно . При подъеме тела массой 50 т малый поршень за время 1,5 мин сделал 200 ходов. Ход малого поршня 20 см, мощность двигателя 4 кВт.
Источник
Помним, (1) что давление в жидкости P = ρ·g·h, (2) если давление в сообщающихся сосудах (в правом и левом колене U образной трубки) одинаково, то жидкость покоится, иначе начинает движение перетекая из одной части сосуда в другую.
Доливая керосин в правое колено трубки мы изменяем уровень воды в левом колене трубки. Но! Вода из правого колена переходит в левое, чтобы скомпенсировать давление создаваемое столбом керосином. Распишем изменение высот столбов жидкости в каждом из колен.
Правое колено:
Высота столба жидкости: h прав. = х + h кер. – h воды., где х-исходная высота столба воды, h кер. -высота столба налитого керосина, h воды. -высота столба воды ушедшей в левое колено сосуда;
Расстояние от края трубки до уровня жидкости: 45 – h кер. + h воды., заметим, что когда жидкость из трубки уходит, то это расстояние увеличивается, когда жидкость доливают, то “зазор” между поверхностью жидкости и краем трубки, увеличивается.
Левое колено:
Высота столба жидкости: h лев. = х + h воды.;
Расстояние от края трубки до уровня жидкости: 45 – h воды.
В тот момент, когда жидкости покоятся, давления в правом и левом колене сосуда равны.
P прав. = P лев.
ρ воды·g·(х – h воды.) + ρ кер. ·g·h кер. = ρ воды ·g·(х + h воды.).
Домножим правую и левую части уравнения на дробь 1/g, раскроем скобки и получим:
ρ воды·х – ρ воды·h воды. + ρ кер. ·h кер. = ρ воды. ·х + ρ воды. ·h воды.
Сгруппируем в правой части уравнения все слагаемые с ρ воды., а в левой с ρ кер.
ρ кер. ·h кер. = ρ воды. ·х + ρ воды. ·h воды. – ρ воды·х + ρ воды·h воды.
ρ кер. ·h кер. = 2·ρ воды. ·h воды.
Плотность пресной воды 1 г/см³ плотность керосина пусть будет 0,8 г/см³ (точное значение зависит от марки керосина).
0,8·h кер. = 2·1·h воды.;
h кер. = (2·1·h воды.) /0,8;
h кер. = 2,5·h воды. [*]
Керосин легче воды, его столб будет выше, поэтому первым исчезнет зазор в правом колене.
45 – h кер. + h воды. = 0, то есть
h кер. = 45 + h воды. [**]
Левые и правые части уравнений [*] и [**] равны, объединим их в одно уравнение.
2,5·h воды. = 45 + h воды.
Упростим выражение.
2,5·h воды. – h воды. = 45;
(2,5 – 1)·h воды. = 45;
h воды. = 45/1,5 = 30 см;
h кер. = 45 + h воды. = 45+30=75 см.
Задача №2
Условие в этой задаче не полное, поэтому она, записанная как есть, имеет множество решений.
p ртути = ρ ртути ·g·h ртути = 13600 кг/м³ · 9,8 Н/кг · 0,01 м = 1333 Па
(Учебник физики 7 класс, Перышкин А. В., 2006 г., стр. 102).
p общ. = p воды + p керосина = ρ воды ·g·h воды + ρ кер. ·g·h кер. = 9800·h воды +7840·h кер.
1333= 9800·h воды +7840·h кер.
Из Вашего условия большего мы получить не сможем.
Задача №3
Сила тяжести F=mg; сообщающиеся сосуды с различным сечением используют в гидравлических машинах для развития больших сил, перегоняя поршнями жидкость из сосуда с малым сечением (площадью поперечного сечения) в сосуд с большим сечением F₂/F₁ = S₂/S₁.
Доливая керосин сверху мы его массой действуем как-бы на поршень 1.
F₁ = Fтяж. керосина. = m кер. ·g = V кер. ·ρ кер. ·g = S₁ · h кер. · ρ кер. ·g.
F₂ = Fтяж. воды. = S₂ · h воды. · ρ воды. ·g.
Жидкость в сосудах покоится, следовательно, сила с которой действует керосин уравновешена силой с которой действует столб воды:
F₁ = F₂;
S₁ · h кер. · ρ кер. ·g = S₂ · h воды. · ρ воды. ·g.
(h кер. · ρ кер. ·g) / (h воды. · ρ воды. ·g) = S₂/S₁;
(???высота керосина 2 см или 0,2 см ??? Будем считать =2 см)
(0,02·0,8·9,8)/(h воды. ·1·9,8) = 3/1
Выразим неизвестную величину:
(0,02·0,8·9,8)·1= 3·(h воды. ·1·9,8)
h воды. = ((0,02·0,8·9,8)·1)/(3·(1·9,8)) = 0,016/3 = 0,005(3) м ≈ 0,53 см. – изменение уровня воды в широком сосуде.
Источник
Решебник по физике Л.А. Кирик Самостоятельные и контрольные работы
1. а) Два сосуда одинаковой формы и размеров установлены так, как показано на рисунке. Что можно сказать: а) о массах воды в сосудах; б) о давлении на дно сосудов; в) о силах давления на дно сосудов?
а) массы одинаковы
б) давление на дно одинаково
в) сила давления на дно в первом сосуде больше, так как площадь дна больше
б) В сосуде находится один над другим три слоя несмешивающихся жидкостей: воды, керосина и ртути. Высота каждого слоя 5 см. Сделайте пояснительный рисунок и укажите на нем порядок расположения слоев. Определите давление жидкостей на дно сосуда и на глубине 7,5 см.
2. а) Под колоколом воздушного насоса находится сосуд, закупоренный пробкой. Почему при интенсивном выкачивании воздуха из-под колокола пробка может вылететь (см. рисунок)?
Давление под колоколом на пробку по мере выкачивания воздуха уменьшается, а внутри колбы остается постоянным. Когда сила давления газа, обусловленная разностью давлений, превысит максимальное значение силы трения покоя пробки о стекло, пробка вылетит.
б) Кубик с длиной ребра 10 см погружен в воду так, что его нижняя грань находится на глубине 25 см. С какой силой вода давит на нижнюю грань?
3. а) Будет ли гидравлический пресс работать на Луне? Если да, то будет ли какое-то различие в его работе на Луне по сравнению с работой на Земле?
Давление пресса на Луне будет меньше, чем на Земле, так как сила тяжести на Луне меньше.
б) В левое колено U-образной трубки с водой долили слой керосина высотой 20 см. На сколько поднимется уровень воды в правом колене?
4. а) Сосуды имеют одинаковые площади дна. Что можно сказать: а) о массах воды в сосудах; б) о давлении на дно сосудов; в) о силах давления на дно сосудов?
а) масса в 1-ом сосуде больше
б) давления одинаковы
в) силы давления одинаковы, так как площади дна равны
б) Малый поршень гидравлического пресса площадью 2 см2 под действием внешней силы опустился на 16 см. Площадь большего поршня 8 см2. Определите вес груза, поднятого поршнем, если на малый поршень действовала сила 200 Н. На какую высоту был поднят груз?
5. а) Справедлив ли закон сообщающихся сосудов в условиях невесомости?
Нет. В состоянии невесомости вес тела равен 0, следовательно, жидкость не будет оказывать давление.
б) Со дна аквариума убрали камень массой 780 г. В результате давление на дно сосуда уменьшилось на 50 Па. Какова плотность камня, если известно, что длина аквариума 30 см, а ширина 20 см? Камень был погружен в воду полностью.
6. а) Что вы можете сказать о величине давления и силах давления на дно сосуда во всех трех отсеках, изображенных на рисунке?
Давление зависит только от высоты сосуда и плотности жидкости. Сила давления на дно будет больше там, где площадь дна больше. => Давление одинаково во всех трёх отсеках, сила давления в 1-ом сосуде больше, чем во 2,3 отсеках.
б) В цилиндрических сообщающихся сосудах находится вода. Площадь поперечного сечения широкого сосуда в 4 раза больше площади поперечного сечения узкого сосуда. В узкий сосуд наливают керосин, который образует столб высотой 20 см. На сколько повысится уровень воды в широком сосуде и на сколько опустится в узком?
Пусть относительно начального уровня воды в сосудах в узком сосуде уровень воды понизится на h2, а в широком повысится на h1. Тогда давление столба керосина высотой Н в узкой трубке будет равно g ρк Н, давление воды в широкой трубке равно g ρв (h1 + h2), где ρк – плотность керосина и ρв – плотность воды. Так как жидкости находятся в равновесии, то
g ρк Н = g ρв (h1 + h2), или ρк Н = ρв (h1 + h2)
Воду считаем несжимаемой жидкостью, поэтому уменьшение объёма в узкой трубке площадью S должно быть равно увеличению объёма в широкой трубке площадью 4S:
Sh2 = 4Sh1, или h2 = 4h1.
Определим h1 = ρк Н/ 5 ρв.
Получаем h1 = 3,2 см и h2 = 12,8 см.
Источник

Сообщающиеся сосуды – это сосуды, соединенные между собой ниже уровня жидкости в каждом из сосудов. Таким образом жидкость может перемещаться из одного сосуда в другой.
Перед тем как понять принцип действия сообщающихся сосудов и варианты их использования необходимо определиться в понятиях, а точнее разобраться с основным уравнением гидростатики.
Итак, сообщающиеся сосуды имеют одно общее дно и закон о сообщающихся сосудах гласит:
Какую бы форму не имели такие сосуды, на поверхности однородных жидкостей в состоянии покоя на одном уровне действует одинаковое давление.
Для иллюстрации этого закона и возможностей его применения начнем с рассмотрения основного уравнения гидростатики.
Основное уравнение гидростатики

P = P1 + ρgh
где P1 – это среднее давление на верхний торец призмы,
P – давление на нижний торец,
g – ускорение свободного падения,
h – глубина погружения призмы под свободной поверхностью жидкости.
ρgh – сила тяжести (вес призмы).
Звучит уравнение так:
Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.
Из написанного выше уравнения следует, что если давление, например в верхней точке изменится на какую-то величину ΔР, то на такую же величину изменится давление в любой другой точке жидкости
Доказательство закона сообщающихся сосудов
Возвращаемся к разговору про сообщающиеся сосуды.

Предположим, что имеются два сообщающихся сосуда А и В, заполненные различными жидкостями с плотностями ρ1 и ρ2. Будем считать, что в общем случае сосуды закрыты и давления на свободных поверхностях жидкости в них соответственно равны P1 и P2.
Пусть поверхностью раздела жидкостей будет поверхность ab в сосуде А и слой жидкости в этом сосуде равен h1. Определим в заданных условиях уровень воды в сообщающихся сосудах – начнем с сосуда В.
Гидростатическое давление в плоскости ab, в соответствии с уравнение гидростатики
P = P1 + ρgh1
если определять его, исходя из известного давления P1 на поверхность жидкости в сосуде А.
Это давление можно определить следующим образом
P = P2 + ρgh2
где h2 – искомая глубина нагружения поверхности ab под уровнем жидкости в сосуде В. Отсюда выводим условие для определения величины h2
P1 + ρ1gh1 = P2 + ρ2gh2
В частном случае, когда сосуды открыты (двление на свободной поверхности равно атмосферному), а следовательно P1 = P2 = Pатм , имеем
ρ1h1 = ρ2h2
или
ρ1 / ρ2 = h2 / h1
т.е. закон сообщающихся сосудов состоит в следующем.
В сообщающихся сосудах при одинаковом давлении на свободных поверхностях высоты жидкостей, отсчитываемые от поверхности раздела, обратно пропорциональны плотностям жидкостей.
Свойства сообщающихся сосудов

Если уровень в сосудах одинаковый, то жидкость одинаково давит на стенки обоих сосудов. А можно ли изменить уровень жидкости в одном из сосудов.
Можно. С помощью перегородки. Перегородка, установленная между сосудами перекроет сообщение. Далее доливая жидкость в один из сосудов мы создаем так называемый подпор – давление столба жидкости.
Если затем убрать перегородку, то жидкость начнет перетекать в тот сосуд где её уровень ниже до тех пор пока высота жидкости в обоих сосудах не станет одинаковой.
В быту этот принцип используется например в водонапорной башне. Наполняя водой высокую башню в ней создают подпор. Затем открывают вентили, расположенные на нижнем этаже и вода устремляется по трубопроводам в каждый подключенный к водоснабжению дом.
Приборы основанные на законе сообщающихся сосудов

На принципе сообщающихся сосудов основано устройство очень простого прибора для определения плотности жидкости. Этот прибор представляет собой два сообщающихся сосуда – две вертикальные стеклянные трубки А и В, соединенные между собой изогнутым коленом С. Одна из вертикальных трубок заполняется исследуемой жидкостью, а другая жидкостью известной плотности ρ1 (например водой), причем в таких количествах, чтобы уровни жидкости в среднем колене находились на одной и той же отметке прибора 0.
Затем измеряют высоты стояния жидкостей в трубках над этой отметкой h1 и h2. И имея ввиду, что эти высоты обратно пропорциональны плотностям легко находят плотность исследуемой жидкости.

В случае, когда оба сосуде заполнены одной и той же жидкостью – высоты, на которые поднимется жидкость в сообщающихся сосудах, будут одинаковы. На этом принципе основано устройство так называемого водометного стекла А. Его применяют для определения уровня жидкости в закрытых сосудах, например резервуарах, паровых котлах и т.д.
Принцип сообщающихся сосудов заложен в основе ряда других приборов, предназначенных для измерения давления.
Применение сообщающихся сосудов

Простейшим прибором жидкостного типа является пьезометр, измеряющий давление в жидкости высотой столба той же жидкости.
Пьезометр представляет собой стеклянную трубку небольшого диаметра (обычно не более 5 мм), открытую с одного конца и вторым концом присоединяемую к сосуду, в котором измеряется давление.
Высота поднятия жидкости в пьезометрической трубке – так называемая пьезометрическая высота – характеризует избыточное давление в сосуде и может служить мерой для определения его величины.
Пьезометр – очень чувствительный и точный прибор, но он удобен только для измерения небольших давлений. При больших давлениях трубка пьезометра получается очень длинной, что усложняет измерения.
В этом случае используют жидкостные манометры, в которых давление уравновешивается не жидкостью, которой может быть вода в сообщающихся сосудах, а жидкостью большей плотности. Обычно такой жидкостью выступает ртуть.

Так как плотность ртути в 13,6 раз больше плотности воды и при измерении одних и тех же давлений трубка ртутного манометра оказывается значительно короче пьезометрической трубки и сам прибор получается компактнее.
В случае если необходимо измерить не давление в сосуде, а разность давлений в двух сосудах или, например, в двух точках жидкости в одном и том же сосуде применяют дифференциальные манометры.
Сообщающиеся сосуды находят применение в водяных и ртутных приборах жидкостного типа, но ограничиваются областью сравнительно небольших давлений – в основном они применяются в лабораториях, где ценятся благодаря своей простоте и высокой точности.

Когда необходимо измерить большое давление применяются приборы основанные на механических принципах. Наиболее распространенный из них – пружинный манометр. Под действием давления пружина манометра частично распрямляется и посредством зубчатого механизма приводит в движение стрелку, по отклонению которой на циферблате показана величина давления.
Видео по теме
Ещё одним устройством использующим принцип сообщающихся сосудов хорошо знакомым автолюбителем является гидравлический пресс(домкрат). Конструктивно он состоит из двух цилиндров: одного большого, другого маленького. При воздействии на поршень малого цилиндра на большой передается усилие во столько раз большего давления во сколько площадь большого поршня больше площади малого.
Вместе со статьей “Закон сообщающихся сосудов и его применение.” читают:
Источник
Глава 3. Давление твёрдых тел, жидкостей и газов
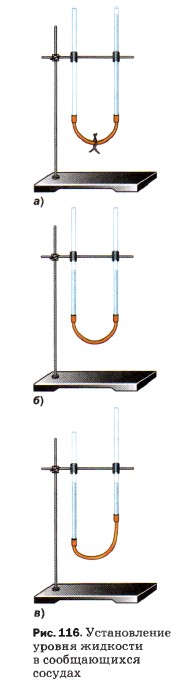
На рисунке 116 изображены два сосуда, соединённые между собой резиновой трубкой. Такие сосуды называют сообщающимися. Лейка, чайник, кофейник — примеры сообщающихся сосудов (рис. 117). Из опыта мы знаем, что вода, налитая, например, в лейку, стоит всегда в резервуаре лейки и в боковой трубке на одном уровне.
С сообщающимися сосудами можно проделать следующий простой опыт. В начале опыта (рис. 116, а) резиновую трубку в середине зажимают и в одну из трубок наливают воду. Затем зажим открывают, и вода начинает перетекать в другую трубку до тех пор, пока поверхности воды в обеих трубках не установятся на одном уровне (рис. 116, б). Можно закрепить одну из трубок в штативе, а другую поднимать, опускать или наклонять в стороны. И в этом случае, как только жидкость успокоится, её уровни в обеих трубках будут одинаковыми (рис. 116, в).
В сообщающихся сосудах любой формы и сечения поверхности однородной жидкости устанавливаются на одном уровне (при условии, что давление воздуха над жидкостью одинаково) (рис. 118).
Это можно обосновать следующим образом. Жидкость покоится, не перемещаясь из одного сосуда в другой (см. рис. 116). Значит, давления в обоих сосудах на любом уровне одинаковы. Жидкость в обоих сосудах одна и та же, т. е. имеет одинаковую плотность. Следовательно,

должны быть одинаковы и её высоты. Когда мы поднимаем один сосуд или доливаем в него жидкость, то давление в нём увеличивается и жидкость перемещается в другой сосуд до тех пор, пока давления не станут одинаковыми.

Примером сообщающихся сосудов могут служить шлюзы, которые воздвигают для прохода судов в обход плотин гидроэлектростанций, или каналы, соединяющие реки (рис. 122).
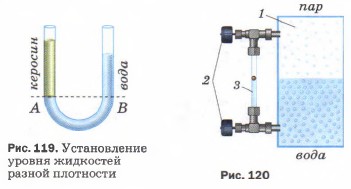
Если в один из сообщающихся сосудов налить жидкость одной плотности, а во второй — другой, то при равновесии уровни этих жидкостей не будут одинаковыми. И это понятно. Мы ведь знаем, что давление жидкости на дно сосуда прямо пропорционально высоте столба и плотности жидкости. А в этом случае плотности жидкостей различны, поэтому высоты столбов этих жидкостей будут различны.
При равенстве давлений высота столба жидкости с большей плотностью будет меньше высоты столба жидкости с меньшей плотностью (рис. 119).
Вопросы
1. Какие примеры сообщающихся сосудов вы можете привести?
2. Как располагаются поверхности однородной жидкости в сообщающихся сосудах?
3. Как располагаются поверхности разнородных жидкостей в сообщающихся сосудах?
Упрожнение 18
1. На рисунке 120 показано водомерное стекло парового котла, где 1 — паровой котёл, 2 — краны, 3 — водомерное стекло. Объясните действие этого прибора.

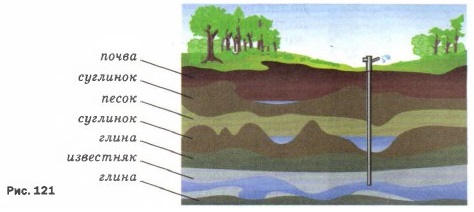
2. На рисунке 121 изображён артезианский колодец в разрезе. Почва, суглинок и песок легко пропускают воду. Глина и известняк, наоборот, водонепроницаемы. Объясните действие такого колодца.

3. Докажите, что в сообщающихся сосудах высоты столбов над уровнем раздела двух разнородных жидкостей (см. рис. 119) обратно пропорциональны плотностям жидкостей.
У к а з а н и е. Используйте формулу для расчёта давления жидкости.
4. Изменится ли расположение жидкости (см. рис. 116), если правый сосуд будет шире левого; уже левого; если сосуды будут иметь разную форму?
Задание
1. Подумайте, как можно простым способом устроить фонтан где-нибудь в парке или во дворе. Начертите схему такого устройства и объясните принцип его действия. Изготовьте модель фонтана.
2. На рисунке 122, (а) дана схема устройства шлюза, а на рисунке 122, (б) — схема шлюзования судов. Рассмотрите рисунки и объясните принцип действия шлюзов. Какое явление используется в работе шлюзов?
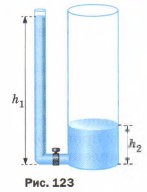
3. В два сосуда налита вода (рис. 123). В каком сосуде давление воды на дно больше и на сколько, если h1 = 40 см, a h2 = 10 см? В каком направлении и до каких пор будет переливаться вода, если открыть кран?
Источник
