В сообщающиеся сосуды площадью сечения s1 и s2
Решебник
ВСЕ
ФИЗИКА
МАТЕМАТИКА
ХИМИЯ
Задача по физике – 1133
Из горизонтальной трубы со скоростью $v_{0}$ вытекает вода, содержащая небольшое количество пузырьков воздуха (см. рисунок). Площадь поперечного сечения трубы $S$, а выходного отверстия $S_{0} 
Подробнее
Задача по физике – 1433
Доказать, что в однородной жидкости на одной горизонтали давление одинаково.
Подробнее
Задача по физике – 1434
В сообщающиеся сосуды налита ртуть, плотность которой $rho_{р}$. Сечения сосудов $S_{1}$ и $S_{2}$. В первый сосуд наливают воду, плотностью $rho_{в}$. Высота столба воды $H$. На какую высоту поднимется уровень ртути во втором сосуде?
Подробнее
Задача по физике – 1435
Гидравлический пресс, заполненный водой, имеет легкие поршни сечений $S_{1}$ и $S_{2}$. На поршень $S_{1}$ положили груз массой $m$. На какую величину поднимется после этого второй поршень?
Подробнее
Задача по физике – 1436
Куб, наполовину наполненный водой, двигают горизонтально с ускорением $a$. Определить форму поверхности воды в кубе.
Подробнее
Задача по физике – 1437
Найдите форму поверхности жидкости в вертикально расположенном цилиндрическом стакане, который вращается вместе с жидкостью вокруг своей оси с угловой скоростью $omega$.
Подробнее
Задача по физике – 1438
Вес однородного тела в воде в $n$ раз меньше, чем в воздухе. Чему равна плотность материала тела? Выталкивающей силой воздуха пренебречь. Плотность воды $rho$.
Подробнее
Задача по физике – 1439
На границе раздела двух жидкостей с плотностями $rho_{1}$ и $rho_{2}$ плавает шайба из материала плотности $rho$, причем $rho_{1} Высота шайбы $h$ Определить глубину погружения во вторую жидкость.
Подробнее
Задача по физике – 1440
В сообщающиеся сосуды диаметрами $d_{1}$ и $d_{2}$ налита жидкость плотности $rho$. На сколько поднимется уровень жидкости в сосудах, если в один из сосудов положить тело массы $M$ из материала, плотность которого меньше $rho$?
Подробнее
Задача по физике – 1441
На дне водоема находится тело массой $m$ со средней плотностью $rho$, полностью погруженное в воду. Плоская часть поверхности тела площадью $S$ плотно прилегает ко дну так, что вода не подтекает. С какой силой тело давит на дно? Глубина водоема $h$.
Подробнее
Задача по физике – 1442
Определите натяжение нижней лески у поплавка, изображенного на рисунке, если поплавок погружен в воду на 2/3 своей длины. Масса поплавка $M$.
Подробнее
Задача по физике – 1443
Какую работу $A$ надо совершить, чтобы вдвинуть пробку на длину $l$? Известны: радиус цилиндрического стакана $R$, плотность жидкости $rho$, радиус пробки $r$, величина $h$ (см. рис.).
Подробнее
Задача по физике – 1444
Внутри тонкостененного сферического баллона радиуса $R$ находится газ под давлением $P$. Разрежем мысленно баллон плоскостью на две равные части. С какой силой $F$ одна половина оболочки баллона удерживает другую? Рассмотреть два случая: 1) внешнее давление отсутствует и 2) внешнее давление равно $P_{0}$.
Подробнее
Задача по физике – 1445
В полусферический колокол, плотно лежащий на столе, наливают через маленькое отверстие наверху жидкость. Когда жидкость доходит до отверстия, она приподнимает колокол и начинает вытекать снизу. Найти массу колокола, если его внутренний диаметр $P$, а плотность жидкости $rho$.
Подробнее
Задача по физике – 1446
Почему сосиска при варении лопается вдоль, а не поперек?
Подробнее
Источник
После того как Паскаль провел ряд опытов по измерению атмосферного давления, он решил сконструировать «новую машину для увеличения сил». Его изобретение позволило создать гидравлический пресс (от греческого слова «гидравликос» — водяной).
Гидравлический пресс — это машина для обработки материалов давлением, приводимая в действие сдавливаемой жидкостью.
Чтобы понять принцип действия гидравлического пресса, рассмотрим рисунок 127. На нем изображены соединенные между собой два цилиндра с поршнями, имеющими разные площади сечения S1 и S2. В цилиндрах находится вода или минеральное масло.
Пусть F1 и F2 — силы, действующие на поршни со стороны находящихся на них гирь. Докажем, что жидкость в цилиндрах будет находиться в равновесии лишь тогда, когда сила, действующая на большой поршень, во столько раз превышает силу, действующую на меньший поршень, во сколько раз площадь большего поршня превышает площадь меньшего поршня. Для этого заметим, что жидкость будет оставаться в равновесии только тогда, когда давления под поршнями будут одинаковыми:
p1 = p2
Но каждое из этих давлений можно выразить через силу и площадь:
что и требовалось доказать.
Отношение F2/F1 характеризуетвыигрыш в силе, получаемый в данной машине. Согласно полученной формуле выигрыш в силе определяется отношением площадей S2/S1. Поэтому,чем больше отношение площадей поршней, тем больше выигрыш в силе.
Например, если площадь малого поршня S1 = 5 см2, а площадь большего поршня S2 = 500 см2, то выигрыш в силе будет составлять сто раз! Установив этот удивительный факт, Паскаль написал, что с помощью изобретенной им машины «один человек, надавливающий на малый поршень, уравновесит силу ста человек, надавливающих на поршень, в сто раз больший, и тем самым преодолеет силу девяносто девяти человек». Это открытие и легло в основу принципа действия гидравлического пресса.
Устройство гидравлического пресса показано на рисунке 128. Цифрой 4обозначен манометр, служащий для измерения давления жидкости внутри пресса; 5 — предохранительный клапан, автоматически открывающийся, когда это давление превышает допустимое значение.
Действие гидравлического пресса основано на законе Паскаля. Прессуемое тело 3 помещают на платформу, соединенную с большим поршнем 2. При действии некоторой силы F1 на малый поршень 1 в узком цилиндре пресса создается избыточное давление p = F1/S1. По закону Паскаля это давление передается во второй цилиндр и на поршень 2 начинает действовать сила:
Так как площадь второго поршня существенно превышает площадь первого поршня, то сила F2 оказывается значительно больше силы F1. Под действием силы F2 поршень 2 начинает подниматься и сдавливает прессуемое тело.
Последующие перекачивания жидкости из узкого цилиндра в широкий осуществляются с помощью периодических нажатий на рычаг 8. После каждого нажатия рычаг следует возвращать в исходное положение. При его подъеме малый поршень перемещается вверх, клапан 6открывается и в пространство, находящееся под поршнем, из сосуда 9засасывается очередная порция жидкости. При опускании рычага поршень 1 перемещается вниз и сдавливаемая жидкость закрывает клапан 6; при этом клапан 7открывается и часть жидкости переходит в широкий цилиндр.
Впервые гидравлические прессы стали применяться на практике в конце XVIII — начале XIX в. Современная техника уже немыслима без них. Они используются в металлообработке для ковки слитков, листовой штамповки, выдавливания труб и профилей, прессования порошковых материалов. С помощью гидравлических прессов получают фанеру, картон и искусственные алмазы.
1. Что такое гидравлический пресс? 2. Чем определяется выигрыш в силе, даваемый гидравлическим прессом (при отсутствии трения)? 3. Расскажите о применении гидравлического пресса. 4.
изображена схема автомобильного гидравлического тормоза (1 — тормозная педаль, 2 — цилиндр с поршнем, 3 — тормозной цилиндр, 4 — тормозные колодки, 5 — тормозные барабаны, 6 — пружина). Цилиндры и трубки заполнены специал
Источник
4.2. Элементы гидростатики
4.2.5. Сообщающиеся сосуды
Сообщающимися называются сосуды, соединенные между собой каналом, заполненным жидкостью.
Для сообщающихся сосудов справедлив закон сообщающихся сосудов: высоты взаимно уравновешенных столбов разнородных жидкостей обратно пропорциональны плотностям этих жидкостей:
h1h2=ρ2ρ1,
где h1 — высота столба жидкости плотностью ρ1; h2 — высота столба жидкости плотностью ρ2.
Указанный закон справедлив в отсутствие сил поверхностного натяжения.
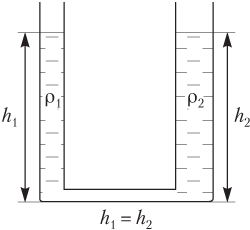
Если сообщающиеся сосуды заполнены однородной жидкостью
ρ1 = ρ2,
то свободные поверхности жидкости устанавливаются на одном уровне, независимо от формы сосудов (рис. 4.14):
h1 = h2,
где h1 — высота столба жидкости в левом колене; h2 — высота столба жидкости в правом колене сообщающихся сосудов.
Рис. 4.14
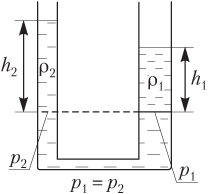
Если сообщающиеся сосуды заполнены разнородными жидкостями
ρ1 ≠ ρ2,
то свободные поверхности жидкостей, независимо от формы сосуда (рис. 4.15), устанавливаются так, что выполняется отношение
h1h2=ρ2ρ1,
где h1 — высота столба жидкости плотностью ρ1; h2 — высота столба жидкости плотностью ρ2.
Рис. 4.15
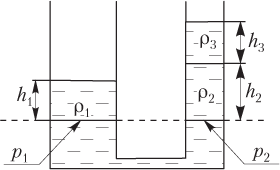
Если сообщающиеся сосуды заполнены несколькими жидкостями (например, как показано на рис. 4.16), то гидростатическое давление на одном уровне (отмеченном пунктиром) в левом колене определяется формулой
p1 = ρ1gh1,
в правом колене —
p2 = ρ2gh2 + ρ3gh3.
Рис. 4.16
Равенство давлений на указанном уровне
p1 = p2
позволяет записать тождество:
ρ1h1 = ρ2h2 + ρ3h3.
Пример 28. Два высоких сосуда, диаметр одного из которых в два раза больше диаметра второго, в нижней части соединены тонким шлангом. Площадь сечения узкого сосуда равна 10 см2. Система заполнена некоторым количеством жидкости плотностью 1,6 г/см3. Найти, на сколько миллиметров повысится уровень жидкости в каждом из сосудов, если в систему добавить 0,12 кг той же жидкости.
Решение. В сообщающихся сосудах однородная жидкость устанавливается на одном уровне.
Добавление в систему некоторого количества жидкости массой m приводит к ее распределению по двум сосудам в соответствии с площадью их поперечного сечения:
- в первом сосуде оказывается масса жидкости
m1 = ρV1 = ρ∆h1S1,
где ρ — плотность жидкости; V1 = S1∆h1 — объем жидкости в первом сосуде; S1 — площадь поперечного сечения первого сосуда; ∆h1 — повышение уровня жидкости в первом сосуде;
- во втором сосуде оказывается масса жидкости
m2 = ρV2 = ρ∆h2S2,
где V2 = S2∆h2 — объем жидкости во втором сосуде; S2 — площадь поперечного сечения второго сосуда; ∆h2 — повышение уровня жидкости во втором сосуде.
Повышение уровней жидкости в обоих сосудах одинаково:
∆h1 = ∆h2 = ∆h,
поэтому масса жидкости, добавленной в систему, определяется формулой
m = m1 + m2 = ρ∆h(S1 + S2).
Выразим отсюда искомое значение ∆h:
Δh=mρ(S1+S2).
Площади поперечного сечения сосудов связаны с их диаметрами формулой:
- для первого (широкого) сосуда
S1=πd124,
- для второго (узкого) сосуда
S2=πd224,
где d1 = 2d2 — диаметр первого (широкого) сосуда; d2 — диаметр второго (узкого) сосуда.
Отношение площадей
S1S2=πd1244πd22=d12d22=(d1d2)2=(2d2d2)2=4
позволяет найти площадь широкого сосуда:
S1 = 4S2.
Подставив S1 в формулу для ∆h
Δh=mρ(4S2+S2)=m5ρS2,
рассчитаем значение высоты, на которую повысится уровень жидкости в сосудах:
Δh=0,125⋅1,6⋅103⋅10⋅10−4=15⋅10−3 м=15 мм.
Пример 29. Два высоких сосуда, диаметр одного из которых в два раза больше диаметра другого, в нижней части соединены тонким шлангом. Площадь сечения широкого сосуда составляет 10 см2. Система заполнена жидкостью плотностью 6,0 г/см3. В узкий сосуд добавляют 0,12 кг жидкости плотностью 2,0 г/см3, а затем — 0,12 кг жидкости плотностью 4,0 г/см3. Найти разность уровней жидкостей в сосудах.
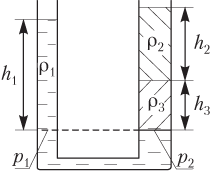
Решение. В сообщающихся сосудах неоднородная жидкость устанавливается на разных уровнях таким образом, что гидростатическое давление на выбранном уровне оказывается одинаковым:
p1 = p2,
где p1 — давление в широком сосуде; p2 — давление в узком сосуде.
На рисунке пунктирной линией обозначен уровень, на котором будем рассчитывать гидростатическое давление в широком и узком сосудах.
Гидростатическое давление на выбранном уровне:
- в широком сосуде
p1 = ρ1gh1,
где ρ1 — плотность жидкости, заполняющей систему изначально; g — модуль ускорения свободного падения; h1 — высота столба жидкости в широком сосуде;
- в узком сосуде
p2 = ρ2gh2 + ρ3gh3,
где ρ2 — плотность первой жидкости, добавленной в узкий сосуд; h2 — высота столба первой жидкости; ρ3 — плотность второй жидкости, добавленной в узкий сосуд; h3 — высота столба второй жидкости.
Равенство давлений на указанном уровне
ρ1gh1 = ρ2gh2 + ρ3gh3
позволяет определить высоту столба жидкости в широком сосуде:
h1=1ρ1(ρ2h2+ρ3h3),
где высоты жидкостей h2 и h3 определяются соответствующими массами и плотностями:
- для первой жидкости
h2=m2ρ2S2;
- для второй жидкости
h3=m3ρ3S2,
где S2 — площадь поперечного сечения узкого сосуда; m2 — масса первой жидкости, добавленной в узкий сосуд; m3 — масса второй жидкости, добавленной в узкий сосуд.
Подстановка h2 и h3 в формулу для h1 дает
h1=1ρ1(ρ2m2ρ2S2+ρ3m3ρ3S2)=m2+m3ρ1S2.
Площади поперечного сечения сосудов связаны с их диаметрами формулой:
- для широкого сосуда
S1=πd124,
- для узкого сосуда
S2=πd224,
где d1 = 2d2 — диаметр широкого сосуда; d2 — диаметр узкого сосуда.
Отношение площадей
S1S2=πd1244πd22=d12d22=(d1d2)2=(2d2d2)2=4
позволяет найти площадь узкого сосуда:
S2=S14.
Таким образом, высота столба жидкости в широком сосуде определяется выражением
h1=4(m2+m3)ρ1S1.
Высота столба жидкости над указанным уровнем в узком сосуде есть сумма:
h2+h3=m2ρ2S2+m3ρ3S2=4S1(m2ρ2+m3ρ3).
Искомая разность верхних уровней жидкостей в узком (h2 + h3) и широком h1 сосудах рассчитывается по формуле
Δh=(h2+h3)−h1=4S1(m2ρ2+m3ρ3)−4(m2+m3)ρ1S1=
=4S1(m2ρ2+m3ρ3−(m2+m3)ρ1).
Произведем вычисление:
Δh=410⋅10−4(0,122,0⋅103+0,124,0⋅103−0,12+0,126,0⋅103)=0,20 м=20 см.
Источник
Определение
Соединенные между собой сосуды называют сообщающимися.
В таких сосудах жидкость имеет возможность перетекать из одной емкости в другую (рис.1). Форма сообщающихся сосудов может быть самая разная.
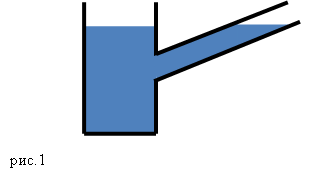
Допустим, что в сообщающиеся сосуды налита однородная жидкость, то в этих сосудах жидкость устанавливается на одном уровне, если давление над поверхностью жидкости одинаково, и не важно какую форму имеют сосуды. В неподвижной жидкости давление ($p$) на одном уровне в сообщающихся сосудах является равным, так как мы знаем, что:
[p=rho gh left(1right),]
где $rho $ – плотность жидкости; $g$ – ускорение свободного падения; $h$ – высота столба жидкости. Так как давление на одном уровне жидкости одинаково, то равными будут и высоты столбов жидкости.
Жидкости разной плотности в сообщающихся сосудах
Допустим, что в сообщающиеся сосуды налили жидкость разной плотности (рис.2(б)). В состоянии равновесия жидкостей, их уровни не будут находиться на одном уровне (высоты столбов жидкости равными не будут).
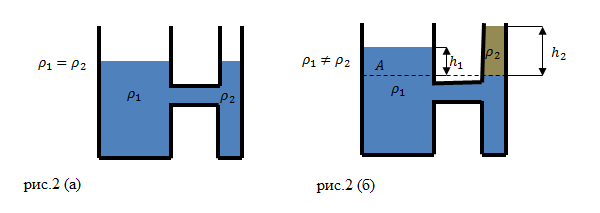
Жидкости в сосудах находятся в равновесии. Давления на уровне A (граница раздела разных жидкостей) (рис. 2 (б)) равны:
[{rho }_1gh_1={rho }_2gh_2left(2right),]
где ${rho }_1$ и ${rho }_2$ – плотности жидкостей. Найдем отношение высот столбов жидкостей в сосудах:
[frac{h_1}{h_2}=frac{{rho }_2}{{rho }_1}left(3right).]
Формула (3) говорит о том, что в сообщающихся сосудах высоты столбиков жидкости над уровнем их раздела обратно пропорциональны плотностям этих жидкостей. При одинаковом давлении над поверхностями жидкостей, высота столба жидкости с меньшей плотностью будет больше, чем высота столба более плотной жидкости.
Гидравлический пресс и другие примеры использования сообщающихся сосудов
В технике сообщающиеся сосуды используют часто. Например, существует такое устройство, как гидравлический пресс. Его изготавливают из двух цилиндров разного радиуса, в которых находятся поршни (рис.3). Сообщающиеся сосуды пресса обычно заполняют минеральным маслом.
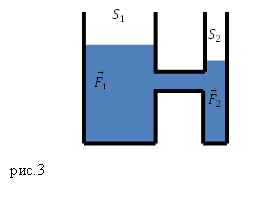
Пусть площадь первого поршня, к которому прикладывают силу ${overline{F}}_1,$ равна $S_1$, площадь второго $S_2$, к нему приложена сила ${overline{F}}_2$. Давление, которое создает первый поршень равно:
[p_1=frac{F_1}{S_1}left(4right).]
Второй поршень давит на жидкость:
[p_2=frac{F_2}{S_2}left(5right).]
Если система находится в состоянии равновесия, то по закону Паскаля давления $p_1$ и $p_2$ равны:
[frac{F_1}{S_1}=frac{F_2}{S_2}left(6right).]
Получим:
[F_1=F_2frac{S_1}{S_2}(7)]
величина первой силы больше модуля силы $F_2$ в $frac{S_1}{S_2}$ раз. Это означает, что при помощи гидравлического пресса, прикладывая небольшую силу к поршню малого сечения, можно получить большую по величине силу, которая будет действовать на большой поршень.
По принципу сообщающихся сосудов, в особенности раньше, действовал водопровод. Такой водопровод сейчас еще можно наблюдать на дачных участках. На относительно большой высоте устанавливается бак с водой, от бака идут водопроводные трубы, закрываемые кранами. Давление у кранов соответствует давлению столба воды, который равен разности высот уровень крана – уровень воды в баке.
Принципом сообщающихся сосудов пользовались, когда проектировали фонтаны, работающие без насосов, шлюзы на реках и каналах.
Примеры задач с решением
Пример 1
Задание. Имеются два цилиндрических сосуда. Высота столба жидкости в одном равна $h_1$, в другом $h_2$. Эти сосуды соединяют трубкой. Насколько изменится высота столба жидкости в левом сосуде, если площадь поперечного сечения его $S_1>S_2$ , $S_2$ – площадь сечения правого сосуда. Объемом трубки пренебречь.
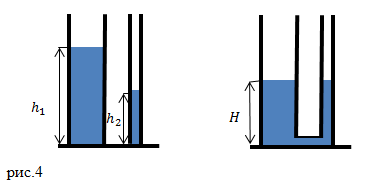
Решение. После того как сосуды соединили, они стали сообщающимися. Часть жидкости из левого сосуда перетечет в правый. Так как жидкость в правом и левом сосудах одна и та же, то уровни жидкости в обоих сосудах будут находиться на одном уровне, то есть высота столбиков жидкости станет равна $H$ в обоих коленах емкости. Определим, какой объем воды перетечет из левого колена в правое:
[Delta V_1=left(h_1-Hright)S_{1 }left(1.1right),]
где $S_{1 }$ – площадь поперечного сечения левого сосуда (сосуда из которого вытекает жидкость). В правом сосуде эта жидкость займет объем равный:
[Delta V_2=left(H-h_2right)S_{2 }left(1.2right),]
где $S_{2 }$ – площадь поперечного сечения правого сосуда. Так как мы считаем, что жидкость не сжимаема, то имеем:
[Delta V_1=Delta V_2left(1.3right).]
Приравниваем правые части выражений (1.2) и (1.1), выражаем высоту столбиков жидкости в правой и левой части сообщающихся сосудов:
[left(h_1-Hright)S_{1 }=left(H-h_2right)S_{2 }to H=frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }} left(1.4right).]
Используя выражение (1.4), изменение высоты жидкости в левом колене, получим равным:
[Delta h=h_1-H=h_1-frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }}=frac{h_1S_1+h_1S_2-h_1S_{1 }-S_{2 }h_2}{S_1+S_{2 }}=]
[=frac{h_1S_2-S_{2 }h_2}{S_1+S_{2 }}=frac{h_1-h_2}{S_1+S_{2 }}S_2.]
Ответ. $Delta h=frac{h_1-h_2}{S_1+S_{2 }}S_2$
Пример 2
Задание. Какой будет сила давления на большой поршень (площадью $S_1$) гидравлического пресса, если площадь его малого поршня равна $S_2$, при этом на него действует сила равная $F_2$?
Решение. В теоретическом разделе сказано, что гидравлический пресс представляет собой систему из сообщающихся сосудов (рис.3). Из закона Паскаля следует, что, прикладывая небольшую силу ($F_2$) к поршню малого сечения ($S_2$) пресса, можно получить большую по величине силу, которая будет действовать на большой поршень ($S_1$):
[F_1=F_2frac{S_1}{S_2}(2.1)]
Ответ. $F_1=F_2frac{S_1}{S_2}$
Читать дальше: условия плавания тел.
Источник