В сообщающиеся сосуды вставлены поршни

В эту статью намеренно сведены задачи про газы в сосудах, закрытых поршнями – легкими и тяжелыми. Под влиянием нагрева газы меняют свое состояние и сдвигают поршни в новое состояние равновесия. Как правило, нужно определить сдвиг поршня или отношение объемов.

Задача 1. В закрытом цилиндрическом сосуде находится газ при нормальных условиях. Сосуд расположен горизонтально и разделен подвижным поршнем в отношении . В каком отношении поршень будет делить сосуд, если его меньшую часть нагреть до , а большую охладить до ?

Понятно, что, раз поршень в равновесии, то давление одинаково с обеих сторон: .

К задаче 1

Состояние газа в левой части сосуда описывается уравнением:

Его количество пропорционально величине:

Количество газа в правой части сосуда пропорционально:

После изменения температур в левой части состояние газа таково:

А в правой:

Возьмем отношение двух последних равенств:

То есть, подставляя и , получим:

Ответ:

Задача 2. В закрытом цилиндрическом сосуде находится газ при температуре . Внутри сосуд перегорожен легким, не проводящим тепло поршнем радиуса см на две части объемами см и см. Поршень находится в равновесии. На какое расстояние переместится поршень, если большую часть газа нагреть на 30К? Температура в другой части не меняется.

Давление изначально одинаково с обеих сторон: .

К задаче 2

Состояние газа в левой части сосуда описывается уравнением:

А в правой части:

После того как газ нагрели, его давление и объем в обеих частях сосуда должны измениться, но по-прежнему давление слева и справа равны:

Возьмем отношение двух последних равенств:

Количество газа в меньшей части сосуда пропорционально величине:

Количество газа в правой части сосуда пропорционально:

Тогда:

Так как объем равен произведению , то

Тогда

Но , поэтому в левой части имеем:

И, так как , то

Наконец,

Но нам неизвестно, поэтому вместо этой величины используем отношение :

Ответ: поршень сдвинется на 0,67 см.

Задача 3. Сосуд с газом плотно закрыт пробкой, площадь сечения которой см. До какой температуры надо нагреть газ, чтобы пробка вылетела из сосуда, если сила трения, удерживающая пробку, Н? Начальное давление воздуха в сосуде Па, начальная температура .

Газ, находящийся в сосуде, изначально оказывает давление на пробку. Только его недостаточно для того, чтобы выдавить ее. Поэтому считаем, что избыточное давление, то есть изменение давления – как раз и выдавит пробку. Тогда

В свою очередь,

А так как процесс изохорный, то

Тогда

И

Тогда

Или

Откуда

Ответ: газ надо нагреть на , то есть до температуры .

Задача 4. В цилиндрическом сосуде с газом находится в равновесии тяжелый поршень. Масса газа и температура под поршнем и над ним одинаковы. Отношение объема над поршнем к объему под поршнем равно 3. Каким будет это отношение, если температуру в сосуде увеличить в 2 раза?

Рассмотрим состояние газа до нагрева. Температура обеих частей одинакова, массы равны, то есть

При этом понятно, что давления разные в обеих частях, так как объемы не одинаковы:

К задаче 4

Следовательно, так как , то

И

Аналогично и после нагрева: так как газ нагревают в обеих частях сосуда, и масса газа в обеих частях одинакова, то можно записать, что

Искомое отношение –

А

И

Подставим давление поршня:

Перейдем к объемам:

Подставим эти соотношения:

Запишем объем после нагрева через приращение объема:

Перейдем к полному объему сосуда:

Теперь мы имеем всего две неизвестных в одном уравнении, и можем разделить все уравнение, например, на :

Где – заметим, что корень должен быть меньше 1 по модулю и при этом положительный, иначе будет потерян физический смысл.

Выбираем в связи с вышеизложенными соображениями второй корень. Тогда .

Найдем оба объема частей сосуда после подогрева:

Наконец, отношение объемов (Алилуйя! Мы сделали это!):

Источник

Задача по физике – 5136

Цилиндр имеет радиус 1 см, площадь сечения 3,14 $см^{2}$ и длину 6,6 см. На половине длины цилиндра впаяли вертикальную тонкую трубку. Правая часть сосуда сообщается с атмосферой (см. рис.). К правой стенке цилиндра с помощью лёгкой пружины жёсткостью 6 Н/м прикрепили массивный тонкий поршень. Длина нерастянутой пружины равна 3 см. Систему установили на упор, находящийся по центру цилиндра. Затем в цилиндр, придерживая его рукой, начали наливать воду. В тот момент, когда масса воды стала равна массе поршня, система оказалась в равновесии. Поршень плотно, но без трения прилегает к стенкам цилиндра. На какой высоте находится вода в трубке?

Подробнее

Задача по физике – 5137

Имеется система сообщающихся сосудов. Левый сосуд плотно закрыт сверху лёгким поршнем, на поршне лежит груз массой 3 кг. В правом сосуде на воде лежит очень лёгкий куб. Длина стороны куба – 10 см. Площади сечений левого и правого сосудов равны соответственно $S_{1} = 0,03 м^{2}$ и $S_{2} = 0,05 м^{2}$. Поршень связан верёвкой с кубом через систему блоков под водой (см. рис.). Первоначально верёвка не провисает. Груз убирают с поршня. На сколько поднимется поршень?

Подробнее

Задача по физике – 5138

Имеется система сообщающихся сосудов (см. рис.). К левому поршню на кронштейне прикреплена пружина жёсткостью $k$, которая другим своим концом соединена с правым поршнем. Когда поршни находятся на одном уровне, пружина не растянута. На сколько растянется пружина, если на правый поршень поместить груз массой $m$? Площади поршней равны $S$ и $2S$. Плотность жидкости – $rho$, ускорение свободного падения $g$. Поршни, кронштейн и пружину считать невесомыми. Считать, что кронштейн может двигаться только вертикально.

Подробнее

Задача по физике – 5139

В водоёме на глубине $h = 10 м$ на краю плоского уступа лежит доска длиной $L = 2 м$, шириной $a = 10 см$ и толщиной $b = 1 см$. Масса доски – 4 кг. Половина доски плотно прижата к поверхности уступа, так что между доской и поверхностью отсутствует вода и воздух (см. рис.). Минимальная сила, которую нужно приложить к середине доски для того, чтобы приподнять прижатую часть, равна $F_{1}$. Если прикладывать силу к правому краю доски, то для того же потребуется сила $F_{2}$. Найти численное значение отношения $F_{1}/F_{2}$.

Подробнее

Задача по физике – 5140

На дно аквариума, заполненного водой, кладут камень (при этом вода через край аквариума не переливается). Как изменится потенциальная энергия воды в аквариуме?

Подробнее

Задача по физике – 5145

Левое плечо лёгкого рычага имеет длину $L_{1} = 8 см$, а правое – $L_{2} = 4 см$. К левому плечу подвешен алюминиевый куб, а к правому – гиря массой $M_{2} = 300 г$ (см. рис.). Когда куб погрузили в воду на 2/3 его объёма, оказалось, что рычаг уравновешен. Найдите объём куба. Плотности алюминия и воды, а также ускорение свободного падения известны.

Подробнее

Задача по физике – 5147

Невесомая жидкость находится между двумя поршнями, неподвижно скреплёнными друг с другом твёрдым стержнем (см. рис.). К малому поршню прикреплён динамометр, к которому приложили силу $F$. Найдите давление в жидкости. Площадь малого поршня – $S_{1}$, площадь большого поршня – $S_{2}$. Атмосферное давление не учитывать.

Подробнее

Задача по физике – 5148

Однородное цилиндрическое бревно радиуса $R$ плавает в воде, причём над поверхностью воды выступает 1/4 его объёма. Из 10 таких же брёвен связали плот (см. рис.). На какую высоту выступает над водой плавающий плот?

Подробнее

Задача по физике – 5149

Два кубика весом $P_{1}$ и $P_{2}$ и рёбрами и $b$ соответственно соединены невесомым тонким стержнем длиной $L$. Система погружена в жидкость плотности $rho$. Где надо поместить точку опоры, чтобы стержень был в равновесии?

Подробнее

Задача по физике – 5150

В прямоугольный сосуд с площадью внутреннего поперечного сечения $S_{0} = 100 см^{2}$ налит столб воды высотой $H = 50 см$ (см. рис.). На поверхности воды плавает невесомый поршень с прямоугольным отверстием, в которое плотно вставлена невесомая трубка прямоугольной формы. Поршень вплотную прилегает к стенкам сосуда. Высота трубки $h = 1 см$, площадь внутреннего поперечного сечения трубки $S = 10 см^{2}$. Поршень начинают опускать вниз с постоянной скоростью $V = 0,1 м/с$. 1) С какой скоростью относительно земли движется верхний уровень воды в трубке? 2) Через какой промежуток времени после приведения поршня в движение вода начнёт переливаться через верхний край трубки?

Подробнее

Задача по физике – 5154

На концы лёгкого стержня длиной 40 см нанизаны два шарика, первый сделан из чугуна, второй -из магния. Стержень погружают в воду и уравновешивают в горизонтальном положении. Точечная опора, на которой уравновешивается система, располагается при этом точно по середине стержня. На сколько нужно передвинуть вдоль стержня второй шарик, чтобы система сохраняла равновесие в воздухе? Плотности чугуна и магния известны.

Подробнее

Задача по физике – 5155

U-образный сосуд с одной стороны закрыт плотно прилегающим к его краям поршнем и заполнен водой, как показано на рис. В трубку B начинают медленно заливать воду. Как только высота уровня воды в нём достигает $h = 5 м$, поршень приподнимается. В этот момент воду заливать прекращают. На какой высоте $h^{ prime}$ установится вода в трубке B? Площади сечения трубки B и узкой части трубки A равны. Площади сечения широкой и узкой частей трубки A равны соответственно $S_{1} = 4 м^{2}$ и $S_{2} = 3 м^{2}$. Высота узкой части трубки A $x = 1 м$.

Подробнее

Задача по физике – 5164

В закрытом сосуде в воде, температура которой равна $0^{ circ} C$, плавает кусок льда массой $m = 0,1 кг$, в который вмёрзла свинцовая дробинка. Когда льдинке передали теплоту 32 кДж, льдинка начала тонуть. Какова была масса дробинки? Плотности льда, свинца, воды, а также удельная теплота плавления льда известны.

Подробнее

Задача по физике – 5184

Труба, сечение которой является квадратом со стороной $a = 20 см$, закрыта поршнем (см. рис.). К трубе присоединена трубка. Часть трубы, находящаяся справа от поршня, полностью заполнена водой, уровень воды в трубке равен $h = 15 см$. Силу какой величины и направления надо прикладывать к поршню, чтобы удерживать его в равновесии? Трение отсутствует.

Подробнее

Задача по физике – 5186

Какова минимальная площадь присоски, с помощью которой можно прикрепить пробковый брусок массы $m$ к горизонтальной поверхности на глубине $h$ под водой (рис.)? Плотность пробки $rho$, плотность воды $rho_{0}$, атмосферное давление $p_{a}$.

Подробнее

Источник

Определение

Соединенные между собой сосуды называют сообщающимися.

В таких сосудах жидкость имеет возможность перетекать из одной емкости в другую (рис.1). Форма сообщающихся сосудов может быть самая разная.

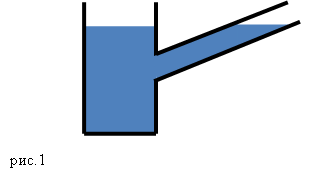
Допустим, что в сообщающиеся сосуды налита однородная жидкость, то в этих сосудах жидкость устанавливается на одном уровне, если давление над поверхностью жидкости одинаково, и не важно какую форму имеют сосуды. В неподвижной жидкости давление ($p$) на одном уровне в сообщающихся сосудах является равным, так как мы знаем, что:

[p=rho gh left(1right),]

где $rho $ – плотность жидкости; $g$ – ускорение свободного падения; $h$ – высота столба жидкости. Так как давление на одном уровне жидкости одинаково, то равными будут и высоты столбов жидкости.

Жидкости разной плотности в сообщающихся сосудах

Допустим, что в сообщающиеся сосуды налили жидкость разной плотности (рис.2(б)). В состоянии равновесия жидкостей, их уровни не будут находиться на одном уровне (высоты столбов жидкости равными не будут).

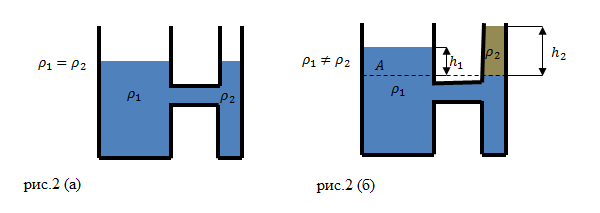
Жидкости в сосудах находятся в равновесии. Давления на уровне A (граница раздела разных жидкостей) (рис. 2 (б)) равны:

[{rho }_1gh_1={rho }_2gh_2left(2right),]

где ${rho }_1$ и ${rho }_2$ – плотности жидкостей. Найдем отношение высот столбов жидкостей в сосудах:

[frac{h_1}{h_2}=frac{{rho }_2}{{rho }_1}left(3right).]

Формула (3) говорит о том, что в сообщающихся сосудах высоты столбиков жидкости над уровнем их раздела обратно пропорциональны плотностям этих жидкостей. При одинаковом давлении над поверхностями жидкостей, высота столба жидкости с меньшей плотностью будет больше, чем высота столба более плотной жидкости.

Гидравлический пресс и другие примеры использования сообщающихся сосудов

В технике сообщающиеся сосуды используют часто. Например, существует такое устройство, как гидравлический пресс. Его изготавливают из двух цилиндров разного радиуса, в которых находятся поршни (рис.3). Сообщающиеся сосуды пресса обычно заполняют минеральным маслом.

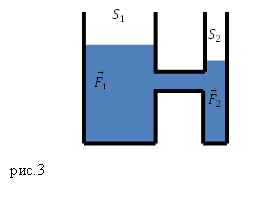
Пусть площадь первого поршня, к которому прикладывают силу ${overline{F}}_1,$ равна $S_1$, площадь второго $S_2$, к нему приложена сила ${overline{F}}_2$. Давление, которое создает первый поршень равно:

[p_1=frac{F_1}{S_1}left(4right).]

Второй поршень давит на жидкость:

[p_2=frac{F_2}{S_2}left(5right).]

Если система находится в состоянии равновесия, то по закону Паскаля давления $p_1$ и $p_2$ равны:

[frac{F_1}{S_1}=frac{F_2}{S_2}left(6right).]

Получим:

[F_1=F_2frac{S_1}{S_2}(7)]

величина первой силы больше модуля силы $F_2$ в $frac{S_1}{S_2}$ раз. Это означает, что при помощи гидравлического пресса, прикладывая небольшую силу к поршню малого сечения, можно получить большую по величине силу, которая будет действовать на большой поршень.

По принципу сообщающихся сосудов, в особенности раньше, действовал водопровод. Такой водопровод сейчас еще можно наблюдать на дачных участках. На относительно большой высоте устанавливается бак с водой, от бака идут водопроводные трубы, закрываемые кранами. Давление у кранов соответствует давлению столба воды, который равен разности высот уровень крана – уровень воды в баке.

Принципом сообщающихся сосудов пользовались, когда проектировали фонтаны, работающие без насосов, шлюзы на реках и каналах.

Примеры задач с решением

Пример 1

Задание. Имеются два цилиндрических сосуда. Высота столба жидкости в одном равна $h_1$, в другом $h_2$. Эти сосуды соединяют трубкой. Насколько изменится высота столба жидкости в левом сосуде, если площадь поперечного сечения его $S_1>S_2$ , $S_2$ – площадь сечения правого сосуда. Объемом трубки пренебречь.

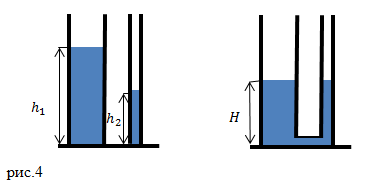
Решение. После того как сосуды соединили, они стали сообщающимися. Часть жидкости из левого сосуда перетечет в правый. Так как жидкость в правом и левом сосудах одна и та же, то уровни жидкости в обоих сосудах будут находиться на одном уровне, то есть высота столбиков жидкости станет равна $H$ в обоих коленах емкости. Определим, какой объем воды перетечет из левого колена в правое:

[Delta V_1=left(h_1-Hright)S_{1 }left(1.1right),]

где $S_{1 }$ – площадь поперечного сечения левого сосуда (сосуда из которого вытекает жидкость). В правом сосуде эта жидкость займет объем равный:

[Delta V_2=left(H-h_2right)S_{2 }left(1.2right),]

где $S_{2 }$ – площадь поперечного сечения правого сосуда. Так как мы считаем, что жидкость не сжимаема, то имеем:

[Delta V_1=Delta V_2left(1.3right).]

Приравниваем правые части выражений (1.2) и (1.1), выражаем высоту столбиков жидкости в правой и левой части сообщающихся сосудов:

[left(h_1-Hright)S_{1 }=left(H-h_2right)S_{2 }to H=frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }} left(1.4right).]

Используя выражение (1.4), изменение высоты жидкости в левом колене, получим равным:

[Delta h=h_1-H=h_1-frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }}=frac{h_1S_1+h_1S_2-h_1S_{1 }-S_{2 }h_2}{S_1+S_{2 }}=] [=frac{h_1S_2-S_{2 }h_2}{S_1+S_{2 }}=frac{h_1-h_2}{S_1+S_{2 }}S_2.]

Ответ. $Delta h=frac{h_1-h_2}{S_1+S_{2 }}S_2$

Пример 2

Задание. Какой будет сила давления на большой поршень (площадью $S_1$) гидравлического пресса, если площадь его малого поршня равна $S_2$, при этом на него действует сила равная $F_2$?

Решение. В теоретическом разделе сказано, что гидравлический пресс представляет собой систему из сообщающихся сосудов (рис.3). Из закона Паскаля следует, что, прикладывая небольшую силу ($F_2$) к поршню малого сечения ($S_2$) пресса, можно получить большую по величине силу, которая будет действовать на большой поршень ($S_1$):

[F_1=F_2frac{S_1}{S_2}(2.1)]

Ответ. $F_1=F_2frac{S_1}{S_2}$

Читать дальше: условия плавания тел.

Источник