В сообщающихся сосудах правое и левое колено состоят

Определение

Соединенные между собой сосуды называют сообщающимися.

В таких сосудах жидкость имеет возможность перетекать из одной емкости в другую (рис.1). Форма сообщающихся сосудов может быть самая разная.

Допустим, что в сообщающиеся сосуды налита однородная жидкость, то в этих сосудах жидкость устанавливается на одном уровне, если давление над поверхностью жидкости одинаково, и не важно какую форму имеют сосуды. В неподвижной жидкости давление ($p$) на одном уровне в сообщающихся сосудах является равным, так как мы знаем, что:

[p=rho gh left(1right),]

где $rho $ – плотность жидкости; $g$ – ускорение свободного падения; $h$ – высота столба жидкости. Так как давление на одном уровне жидкости одинаково, то равными будут и высоты столбов жидкости.

Жидкости разной плотности в сообщающихся сосудах

Допустим, что в сообщающиеся сосуды налили жидкость разной плотности (рис.2(б)). В состоянии равновесия жидкостей, их уровни не будут находиться на одном уровне (высоты столбов жидкости равными не будут).

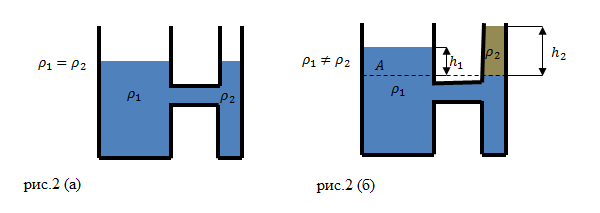
Жидкости в сосудах находятся в равновесии. Давления на уровне A (граница раздела разных жидкостей) (рис. 2 (б)) равны:

[{rho }_1gh_1={rho }_2gh_2left(2right),]

где ${rho }_1$ и ${rho }_2$ – плотности жидкостей. Найдем отношение высот столбов жидкостей в сосудах:

[frac{h_1}{h_2}=frac{{rho }_2}{{rho }_1}left(3right).]

Формула (3) говорит о том, что в сообщающихся сосудах высоты столбиков жидкости над уровнем их раздела обратно пропорциональны плотностям этих жидкостей. При одинаковом давлении над поверхностями жидкостей, высота столба жидкости с меньшей плотностью будет больше, чем высота столба более плотной жидкости.

Гидравлический пресс и другие примеры использования сообщающихся сосудов

В технике сообщающиеся сосуды используют часто. Например, существует такое устройство, как гидравлический пресс. Его изготавливают из двух цилиндров разного радиуса, в которых находятся поршни (рис.3). Сообщающиеся сосуды пресса обычно заполняют минеральным маслом.

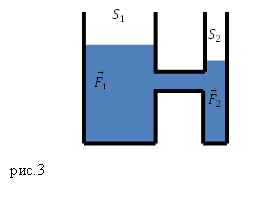
Пусть площадь первого поршня, к которому прикладывают силу ${overline{F}}_1,$ равна $S_1$, площадь второго $S_2$, к нему приложена сила ${overline{F}}_2$. Давление, которое создает первый поршень равно:

[p_1=frac{F_1}{S_1}left(4right).]

Второй поршень давит на жидкость:

[p_2=frac{F_2}{S_2}left(5right).]

Если система находится в состоянии равновесия, то по закону Паскаля давления $p_1$ и $p_2$ равны:

[frac{F_1}{S_1}=frac{F_2}{S_2}left(6right).]

Получим:

[F_1=F_2frac{S_1}{S_2}(7)]

величина первой силы больше модуля силы $F_2$ в $frac{S_1}{S_2}$ раз. Это означает, что при помощи гидравлического пресса, прикладывая небольшую силу к поршню малого сечения, можно получить большую по величине силу, которая будет действовать на большой поршень.

По принципу сообщающихся сосудов, в особенности раньше, действовал водопровод. Такой водопровод сейчас еще можно наблюдать на дачных участках. На относительно большой высоте устанавливается бак с водой, от бака идут водопроводные трубы, закрываемые кранами. Давление у кранов соответствует давлению столба воды, который равен разности высот уровень крана – уровень воды в баке.

Принципом сообщающихся сосудов пользовались, когда проектировали фонтаны, работающие без насосов, шлюзы на реках и каналах.

Примеры задач с решением

Пример 1

Задание. Имеются два цилиндрических сосуда. Высота столба жидкости в одном равна $h_1$, в другом $h_2$. Эти сосуды соединяют трубкой. Насколько изменится высота столба жидкости в левом сосуде, если площадь поперечного сечения его $S_1>S_2$ , $S_2$ – площадь сечения правого сосуда. Объемом трубки пренебречь.

Решение. После того как сосуды соединили, они стали сообщающимися. Часть жидкости из левого сосуда перетечет в правый. Так как жидкость в правом и левом сосудах одна и та же, то уровни жидкости в обоих сосудах будут находиться на одном уровне, то есть высота столбиков жидкости станет равна $H$ в обоих коленах емкости. Определим, какой объем воды перетечет из левого колена в правое:

[Delta V_1=left(h_1-Hright)S_{1 }left(1.1right),]

где $S_{1 }$ – площадь поперечного сечения левого сосуда (сосуда из которого вытекает жидкость). В правом сосуде эта жидкость займет объем равный:

[Delta V_2=left(H-h_2right)S_{2 }left(1.2right),]

где $S_{2 }$ – площадь поперечного сечения правого сосуда. Так как мы считаем, что жидкость не сжимаема, то имеем:

[Delta V_1=Delta V_2left(1.3right).]

Приравниваем правые части выражений (1.2) и (1.1), выражаем высоту столбиков жидкости в правой и левой части сообщающихся сосудов:

[left(h_1-Hright)S_{1 }=left(H-h_2right)S_{2 }to H=frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }} left(1.4right).]

Используя выражение (1.4), изменение высоты жидкости в левом колене, получим равным:

[Delta h=h_1-H=h_1-frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }}=frac{h_1S_1+h_1S_2-h_1S_{1 }-S_{2 }h_2}{S_1+S_{2 }}=] [=frac{h_1S_2-S_{2 }h_2}{S_1+S_{2 }}=frac{h_1-h_2}{S_1+S_{2 }}S_2.]

Ответ. $Delta h=frac{h_1-h_2}{S_1+S_{2 }}S_2$

Пример 2

Задание. Какой будет сила давления на большой поршень (площадью $S_1$) гидравлического пресса, если площадь его малого поршня равна $S_2$, при этом на него действует сила равная $F_2$?

Решение. В теоретическом разделе сказано, что гидравлический пресс представляет собой систему из сообщающихся сосудов (рис.3). Из закона Паскаля следует, что, прикладывая небольшую силу ($F_2$) к поршню малого сечения ($S_2$) пресса, можно получить большую по величине силу, которая будет действовать на большой поршень ($S_1$):

[F_1=F_2frac{S_1}{S_2}(2.1)]

Ответ. $F_1=F_2frac{S_1}{S_2}$

Читать дальше: условия плавания тел.

Источник

4.2. Элементы гидростатики

4.2.5. Сообщающиеся сосуды

Сообщающимися называются сосуды, соединенные между собой каналом, заполненным жидкостью.

Для сообщающихся сосудов справедлив закон сообщающихся сосудов: высоты взаимно уравновешенных столбов разнородных жидкостей обратно пропорциональны плотностям этих жидкостей:

h 1 h 2 = ρ 2 ρ 1 ,

где h1 – высота столба жидкости плотностью ρ1; h2 – высота столба жидкости плотностью ρ2.

Указанный закон справедлив в отсутствие сил поверхностного натяжения.

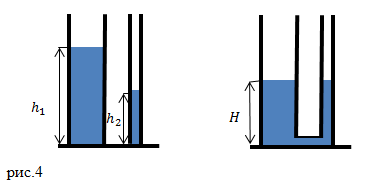
Если сообщающиеся сосуды заполнены однородной жидкостью

ρ1 = ρ2,

то свободные поверхности жидкости устанавливаются на одном уровне, независимо от формы сосудов (рис. 4.14):

h1 = h2,

где h1 – высота столба жидкости в левом колене; h2 – высота столба жидкости в правом колене сообщающихся сосудов.

Рис. 4.14

Если сообщающиеся сосуды заполнены разнородными жидкостями

ρ1 ≠ ρ2,

то свободные поверхности жидкостей, независимо от формы сосуда (рис. 4.15), устанавливаются так, что выполняется отношение

h 1 h 2 = ρ 2 ρ 1 ,

где h1 – высота столба жидкости плотностью ρ1; h2 – высота столба жидкости плотностью ρ2.

Рис. 4.15

Если сообщающиеся сосуды заполнены несколькими жидкостями (например, как показано на рис. 4.16), то гидростатическое давление на одном уровне (отмеченном пунктиром) в левом колене определяется формулой

p1 = ρ1gh1,

в правом колене –

p2 = ρ2gh2 + ρ3gh3.

Рис. 4.16

Равенство давлений на указанном уровне

p1 = p2

позволяет записать тождество:

ρ1h1 = ρ2h2 + ρ3h3.

Пример 28. Два высоких сосуда, диаметр одного из которых в два раза больше диаметра второго, в нижней части соединены тонким шлангом. Площадь сечения узкого сосуда равна 10 см2. Система заполнена некоторым количеством жидкости плотностью 1,6 г/см3. Найти, на сколько миллиметров повысится уровень жидкости в каждом из сосудов, если в систему добавить 0,12 кг той же жидкости.

Решение. В сообщающихся сосудах однородная жидкость устанавливается на одном уровне.

Добавление в систему некоторого количества жидкости массой m приводит к ее распределению по двум сосудам в соответствии с площадью их поперечного сечения:

• в первом сосуде оказывается масса жидкости

m1 = ρV1 = ρ∆h1S1,

где ρ – плотность жидкости; V1 = S1∆h1 – объем жидкости в первом сосуде; S1 – площадь поперечного сечения первого сосуда; ∆h1 – повышение уровня жидкости в первом сосуде;

• во втором сосуде оказывается масса жидкости

m2 = ρV2 = ρ∆h2S2,

где V2 = S2∆h2 – объем жидкости во втором сосуде; S2 – площадь поперечного сечения второго сосуда; ∆h2 – повышение уровня жидкости во втором сосуде.

Повышение уровней жидкости в обоих сосудах одинаково:

∆h1 = ∆h2 = ∆h,

поэтому масса жидкости, добавленной в систему, определяется формулой

m = m1 + m2 = ρ∆h(S1 + S2).

Выразим отсюда искомое значение ∆h:

Δ h = m ρ ( S 1 + S 2 ) .

Площади поперечного сечения сосудов связаны с их диаметрами формулой:

• для первого (широкого) сосуда

S 1 = π d 1 2 4 ,

• для второго (узкого) сосуда

S 2 = π d 2 2 4 ,

где d1 = 2d2 – диаметр первого (широкого) сосуда; d2 – диаметр второго (узкого) сосуда.

Отношение площадей

S 1 S 2 = π d 1 2 4 4 π d 2 2 = d 1 2 d 2 2 = ( d 1 d 2 ) 2 = ( 2 d 2 d 2 ) 2 = 4

позволяет найти площадь широкого сосуда:

S1 = 4S2.

Подставив S1 в формулу для ∆h

Δ h = m ρ ( 4 S 2 + S 2 ) = m 5 ρ S 2 ,

рассчитаем значение высоты, на которую повысится уровень жидкости в сосудах:

Δ h = 0,12 5 ⋅ 1,6 ⋅ 10 3 ⋅ 10 ⋅ 10 − 4 = 15 ⋅ 10 − 3 м = 15 мм.

Пример 29. Два высоких сосуда, диаметр одного из которых в два раза больше диаметра другого, в нижней части соединены тонким шлангом. Площадь сечения широкого сосуда составляет 10 см2. Система заполнена жидкостью плотностью 6,0 г/см3. В узкий сосуд добавляют 0,12 кг жидкости плотностью 2,0 г/см3, а затем – 0,12 кг жидкости плотностью 4,0 г/см3. Найти разность уровней жидкостей в сосудах.

Решение. В сообщающихся сосудах неоднородная жидкость устанавливается на разных уровнях таким образом, что гидростатическое давление на выбранном уровне оказывается одинаковым:

p1 = p2,

где p1 – давление в широком сосуде; p2 – давление в узком сосуде.

На рисунке пунктирной линией обозначен уровень, на котором будем рассчитывать гидростатическое давление в широком и узком сосудах.

Гидростатическое давление на выбранном уровне:

• в широком сосуде

p1 = ρ1gh1,

где ρ1 – плотность жидкости, заполняющей систему изначально; g – модуль ускорения свободного падения; h1 – высота столба жидкости в широком сосуде;

• в узком сосуде

p2 = ρ2gh2 + ρ3gh3,

где ρ2 – плотность первой жидкости, добавленной в узкий сосуд; h2 – высота столба первой жидкости; ρ3 – плотность второй жидкости, добавленной в узкий сосуд; h3 – высота столба второй жидкости.

Равенство давлений на указанном уровне

ρ1gh1 = ρ2gh2 + ρ3gh3

позволяет определить высоту столба жидкости в широком сосуде:

h 1 = 1 ρ 1 ( ρ 2 h 2 + ρ 3 h 3 ) ,

где высоты жидкостей h2 и h3 определяются соответствующими массами и плотностями:

• для первой жидкости

h 2 = m 2 ρ 2 S 2 ;

• для второй жидкости

h 3 = m 3 ρ 3 S 2 ,

где S2 – площадь поперечного сечения узкого сосуда; m2 – масса первой жидкости, добавленной в узкий сосуд; m3 – масса второй жидкости, добавленной в узкий сосуд.

Подстановка h2 и h3 в формулу для h1 дает

h 1 = 1 ρ 1 ( ρ 2 m 2 ρ 2 S 2 + ρ 3 m 3 ρ 3 S 2 ) = m 2 + m 3 ρ 1 S 2 .

Площади поперечного сечения сосудов связаны с их диаметрами формулой:

• для широкого сосуда

S 1 = π d 1 2 4 ,

• для узкого сосуда

S 2 = π d 2 2 4 ,

где d1 = 2d2 – диаметр широкого сосуда; d2 – диаметр узкого сосуда.

Отношение площадей

S 1 S 2 = π d 1 2 4 4 π d 2 2 = d 1 2 d 2 2 = ( d 1 d 2 ) 2 = ( 2 d 2 d 2 ) 2 = 4

позволяет найти площадь узкого сосуда:

S 2 = S 1 4 .

Таким образом, высота столба жидкости в широком сосуде определяется выражением

h 1 = 4 ( m 2 + m 3 ) ρ 1 S 1 .

Высота столба жидкости над указанным уровнем в узком сосуде есть сумма:

h 2 + h 3 = m 2 ρ 2 S 2 + m 3 ρ 3 S 2 = 4 S 1 ( m 2 ρ 2 + m 3 ρ 3 ) .

Искомая разность верхних уровней жидкостей в узком (h2 + h3) и широком h1 сосудах рассчитывается по формуле

Δ h = ( h 2 + h 3 ) − h 1 = 4 S 1 ( m 2 ρ 2 + m 3 ρ 3 ) − 4 ( m 2 + m 3 ) ρ 1 S 1 =

= 4 S 1 ( m 2 ρ 2 + m 3 ρ 3 − ( m 2 + m 3 ) ρ 1 ) .

Произведем вычисление:

Δ h = 4 10 ⋅ 10 − 4 ( 0,12 2,0 ⋅ 10 3 + 0,12 4,0 ⋅ 10 3 − 0,12 + 0,12 6,0 ⋅ 10 3 ) = 0,20 м = 20 см.

Источник

Определение

Сообщающиеся сосуды – сосуды, соединенные между собой или имеющие общее дно.

Уровень жидкости в сообщающихся сосудах одинаков и располагается горизонтально, если:

1. в сосуды налита однородная жидкость
2. поверхности жидкости открыты

3. ни один из сосудов не является капилляром (очень узкой трубкой)

4. в жидкости нет пузырьков с воздухом.

Разные по плотности не смешивающиеся жидкости в сообщающихся сосудах

Если в сообщающихся сосудах находятся неоднородные жидкости, то, согласно закону Паскаля, более плотная жидкость будет оказывать большее давление на дно сосуда и в стороны. Поэтому она будет вытеснять часть жидкости с меньшей плотностью. Равновесие наступит тогда, когда давление столба с более плотной жидкостью сравняется с давлением столба, образованного из двух жидкостей.

По закону Паскаля на любом горизонтальном уровне:

p1 = p2

ρ1gh1 = ρ2gh2

Следовательно:

h2h1=ρ1ρ2

Следовательно, высота столба менее плотной жидкости во столько раз выше высоты столба более плотной жидкости, во сколько более плотная жидкость плотнее менее плотной.

Пример №1. В широкую U-образную трубку с вертикальными прямыми коленами налиты керосин плотностью ρ1 = 800 кг/м3 и вода плотностью ρ2 = 1000 кг/м3 (см. рисунок). На рисунке b = 10 см, H = 30 см. Определите расстояние h.

10 см = 0,1 м

20 см = 0,3 м

Жидкость находится в равновесии. С учетом того, что в первом колене содержится сразу две жидкости:

ρ1g(H – b) + ρ2gb = ρ2gh

Или:

ρ1(H – b) + ρ2b = ρ2h

Отсюда:

h=ρ1(H−b)+ρ2bρ2=800(0,3−0,1)+1000·0,11000=0,26 (м)

Гидравлический пресс

Определение

Гидравлический пресс – простой механизм, дающий выигрыш в силе. Он представляет собой сообщающиеся сосуды разного сечения.

В основе действия гидравлического пресса лежит закон Паскаля. Так как высоты столбов равны, давления в колене малого и большого сечения тоже равны:

pм = pб

Следовательно:

FмSм=FбSб

Fм – сила, действующая на малый поршень (совершает полную работу), Fб – сила, действующая на большой поршень (совершает полезную работу), Sм – площадь малого поршня, Sб – площадь большого поршня.

Работа поршней (без потерь энергии):

Aм = Aб

Fмhм = Fбhб

hм – вертикальное перемещение малого поршня, hб – перемещение большого поршня.

Равенство объемов жидкостей при движении поршней:

Sмhм = Sбhб

КПД (есть потери энергии):

η=AбAм·100%=FбhбFмhм·100%=pбpм·100%

Пример №2. К малому поршню гидравлического пресса приложена сила 10 Н, под действием которой за один ход он опускается на 25 см, вследствие чего большой поршень поднимается на 5 мм. Какая сила давления передается при этом на большой поршень?

25 см = 0,25 м

5 мм = 0,005 м

Так как работа поршней одинакова:

Fмhм = Fбhб

Отсюда:

Fб=Fмhмhб=10·0,250,005=500 (Н).

Атмосферное давление

Атмосфера – воздушная оболочка Земли. Она существует благодаря земному притяжению и беспорядочному движению молекул в газообразном состоянии. В состав атмосферы входят азот, кислород и другие газы. Атмосфера не имеет четкой границы, а плотность воздуха уменьшается с высотой.

Определение

Атмосферное давление – давление «воздушного океана», которое также уменьшается с высотой.

Ртутный барометр

Определение

Ртутный барометр – прибор для определения атмосферного давления, созданный Торричелли. Состоит из стеклянной трубки, запаянной с одного конца, длиной 1 м, заполненной ртутью, а также из широкого сосуда, в который выливается ртуть после поворота трубки.

По свойству сообщающихся сосудов:

pатм = pртути (мм рт. ст.).

Формула для определения атмосферного давления (в паскалях):

pатм = pртgh

pатм – атмосферное давление, pрт – плотность ртути (13600 кг/м3), g – ускорение свободного падения (9,8 м/с2 или округленно – 10 м/с2), h – высота ртутного столба (м).

Дополнительные единицы измерения атмосферного давления:

1 мм рт. ст. = 133 Па

1 атм (атмосфера) = 105 Па

Нормальное атмосферное давление равно: p0 = 105 Па.

Пример №3. С какой силой давит воздух на поверхность письменного стола, длина которого 120 см, ширина – 60 см, если атмосферное давление равно 100 кПа?

Сила давления есть произведение давления на площадь. Поэтому:

F = pS = pab = 105∙1,2∙0,6 = 72 кН.

Задание EF18172 В широкую U-образную трубку, расположенную вертикально, налиты жидкости плотностью ρ1 и ρ2 (см. рисунок). Жидкости не смешиваются. На рисунке b = 15 см, h = 30 см, H = 35 см. Отношение плотности ρ1 к плотности ρ2 равно …

Ответ:

а) 0,67

б) 0,75

в) 0,86

г) 1,33

Алгоритм решения

1.Записать исходные данные.

2.Записать условие равновесия неоднородных жидкостей в сообщающихся сосудах.

3.Выполнить решение задачи в общем виде.

4.Вычислить искомую величину, подставив известные значения.

Решение

Запишем исходные данные:

• Уровень жидкости в левом колене: H = 35 см.

• Уровень жидкости в правом колене: h = 30 см.

• Высота столба более плотной жидкости в левом колене: b = 15 см.

Внимание! В данном случае переводить единицы в СИ необязательно, так как на величину отношения они никак не повлияют.

Запишем условие равновесия. Давление на уровне b в обоих коленах должно быть одинаковое. Поэтому:

ρ1g(H – b) = ρ2g(h – b)

Отсюда:

ρ1ρ2=g(h−b)g(H−b)=h−bH−b=30−1535−15=1520=0,75

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF22683 В комнате находится открытая сверху U-образная трубка, в которую налита ртуть (рис. а). Левое колено трубки плотно закрывают пробкой (рис. б), после чего температура в комнате увеличивается. Что произойдёт с уровнями ртути в коленах трубки? Атмосферное давление считать неизменным. Ответ поясните, указав, какие физические явления и закономерности Вы использовали для объяснения.

Алгоритм решения

1. Установить, что изменится после того, как одно колено сосуда будет закупорено.
2. Установить, что изменится после того, как температура воздуха увеличится.

Решение

Изначально давление, оказываемое атмосферой на поверхность ртути в обоих коленах, равно. Это следует из закона Паскаля и условия равновесия. Когда одно колено сообщающихся сосудов будет закупорено, сначала давление под пробкой будет равно атмосферному давлению. Но при изменении прочих условий уровень жидкостей в коленах не будет одинаков. Это связано с изменением давления, оказываемого на поверхности жидкостей в закупоренном и открытом коленах.

Если же увеличить температуру воздуха, то воздух под пробкой тоже нагреется. От этого его объем увеличится, что приведет к росту давления, которое окажется больше атмосферного на величину, равную ∆p = ρвg∆h. Суммарное давление, оказываемое со стороны закупоренного колена, будет равно сумме атмосферного давления и давления ∆p: pз = pатм + ρвg∆h. Со стороны открытого колена по-прежнему будет оказываться атмосферное давление: pо = pатм. Поэтому избыточное давление под пробкой начнет выталкивать часть ртути из левого колена в правое до тех пор, пока не наступит равновесие. При условии, что диаметр трубок одинаковый, это произойдет тогда, когда уровень ртути в открытой трубке увеличится на высоту ∆h – на ту высоту, на которую понизится уровень ртути в закупоренной трубке.

Ответ: уровень ртути в закрытом колене понизится, а в открытом – понизится.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | ???? Скачать PDF | Просмотров: 603 | Оценить:

Источник