В сообщающихся сосудах уровни однородной жидкости одинаковы

Сообщающиеся сосуды – это сосуды, соединенные между собой ниже уровня жидкости в каждом из сосудов. Таким образом жидкость может перемещаться из одного сосуда в другой.
Перед тем как понять принцип действия сообщающихся сосудов и варианты их использования необходимо определиться в понятиях, а точнее разобраться с основным уравнением гидростатики.
Итак, сообщающиеся сосуды имеют одно общее дно и закон о сообщающихся сосудах гласит:
Какую бы форму не имели такие сосуды, на поверхности однородных жидкостей в состоянии покоя на одном уровне действует одинаковое давление.
Для иллюстрации этого закона и возможностей его применения начнем с рассмотрения основного уравнения гидростатики.
Основное уравнение гидростатики
P = P1 + ρgh
где P1 – это среднее давление на верхний торец призмы,
P – давление на нижний торец,
g – ускорение свободного падения,
h – глубина погружения призмы под свободной поверхностью жидкости.
ρgh – сила тяжести (вес призмы).
Звучит уравнение так:
Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.
Из написанного выше уравнения следует, что если давление, например в верхней точке изменится на какую-то величину ΔР, то на такую же величину изменится давление в любой другой точке жидкости
Доказательство закона сообщающихся сосудов
Возвращаемся к разговору про сообщающиеся сосуды.
Предположим, что имеются два сообщающихся сосуда А и В, заполненные различными жидкостями с плотностями ρ1 и ρ2. Будем считать, что в общем случае сосуды закрыты и давления на свободных поверхностях жидкости в них соответственно равны P1 и P2.
Пусть поверхностью раздела жидкостей будет поверхность ab в сосуде А и слой жидкости в этом сосуде равен h1. Определим в заданных условиях уровень воды в сообщающихся сосудах – начнем с сосуда В.
Гидростатическое давление в плоскости ab, в соответствии с уравнение гидростатики
P = P1 + ρgh1
если определять его, исходя из известного давления P1 на поверхность жидкости в сосуде А.
Это давление можно определить следующим образом
P = P2 + ρgh2
где h2 – искомая глубина нагружения поверхности ab под уровнем жидкости в сосуде В. Отсюда выводим условие для определения величины h2
P1 + ρ1gh1 = P2 + ρ2gh2
В частном случае, когда сосуды открыты (двление на свободной поверхности равно атмосферному), а следовательно P1 = P2 = Pатм , имеем
ρ1h1 = ρ2h2
или
ρ1 / ρ2 = h2 / h1
т.е. закон сообщающихся сосудов состоит в следующем.
В сообщающихся сосудах при одинаковом давлении на свободных поверхностях высоты жидкостей, отсчитываемые от поверхности раздела, обратно пропорциональны плотностям жидкостей.
Свойства сообщающихся сосудов
Если уровень в сосудах одинаковый, то жидкость одинаково давит на стенки обоих сосудов. А можно ли изменить уровень жидкости в одном из сосудов.
Можно. С помощью перегородки. Перегородка, установленная между сосудами перекроет сообщение. Далее доливая жидкость в один из сосудов мы создаем так называемый подпор – давление столба жидкости.
Если затем убрать перегородку, то жидкость начнет перетекать в тот сосуд где её уровень ниже до тех пор пока высота жидкости в обоих сосудах не станет одинаковой.
В быту этот принцип используется например в водонапорной башне. Наполняя водой высокую башню в ней создают подпор. Затем открывают вентили, расположенные на нижнем этаже и вода устремляется по трубопроводам в каждый подключенный к водоснабжению дом.
Приборы основанные на законе сообщающихся сосудов
На принципе сообщающихся сосудов основано устройство очень простого прибора для определения плотности жидкости. Этот прибор представляет собой два сообщающихся сосуда – две вертикальные стеклянные трубки А и В, соединенные между собой изогнутым коленом С. Одна из вертикальных трубок заполняется исследуемой жидкостью, а другая жидкостью известной плотности ρ1 (например водой), причем в таких количествах, чтобы уровни жидкости в среднем колене находились на одной и той же отметке прибора 0.
Затем измеряют высоты стояния жидкостей в трубках над этой отметкой h1 и h2. И имея ввиду, что эти высоты обратно пропорциональны плотностям легко находят плотность исследуемой жидкости.
В случае, когда оба сосуде заполнены одной и той же жидкостью – высоты, на которые поднимется жидкость в сообщающихся сосудах, будут одинаковы. На этом принципе основано устройство так называемого водометного стекла А. Его применяют для определения уровня жидкости в закрытых сосудах, например резервуарах, паровых котлах и т.д.
Принцип сообщающихся сосудов заложен в основе ряда других приборов, предназначенных для измерения давления.
Применение сообщающихся сосудов
Простейшим прибором жидкостного типа является пьезометр, измеряющий давление в жидкости высотой столба той же жидкости.
Пьезометр представляет собой стеклянную трубку небольшого диаметра (обычно не более 5 мм), открытую с одного конца и вторым концом присоединяемую к сосуду, в котором измеряется давление.
Высота поднятия жидкости в пьезометрической трубке – так называемая пьезометрическая высота – характеризует избыточное давление в сосуде и может служить мерой для определения его величины.
Пьезометр – очень чувствительный и точный прибор, но он удобен только для измерения небольших давлений. При больших давлениях трубка пьезометра получается очень длинной, что усложняет измерения.
В этом случае используют жидкостные манометры, в которых давление уравновешивается не жидкостью, которой может быть вода в сообщающихся сосудах, а жидкостью большей плотности. Обычно такой жидкостью выступает ртуть.
Так как плотность ртути в 13,6 раз больше плотности воды и при измерении одних и тех же давлений трубка ртутного манометра оказывается значительно короче пьезометрической трубки и сам прибор получается компактнее.
В случае если необходимо измерить не давление в сосуде, а разность давлений в двух сосудах или, например, в двух точках жидкости в одном и том же сосуде применяют дифференциальные манометры.
Сообщающиеся сосуды находят применение в водяных и ртутных приборах жидкостного типа, но ограничиваются областью сравнительно небольших давлений – в основном они применяются в лабораториях, где ценятся благодаря своей простоте и высокой точности.
Когда необходимо измерить большое давление применяются приборы основанные на механических принципах. Наиболее распространенный из них – пружинный манометр. Под действием давления пружина манометра частично распрямляется и посредством зубчатого механизма приводит в движение стрелку, по отклонению которой на циферблате показана величина давления.
Видео по теме
Ещё одним устройством использующим принцип сообщающихся сосудов хорошо знакомым автолюбителем является гидравлический пресс(домкрат). Конструктивно он состоит из двух цилиндров: одного большого, другого маленького. При воздействии на поршень малого цилиндра на большой передается усилие во столько раз большего давления во сколько площадь большого поршня больше площади малого.
Вместе со статьей “Закон сообщающихся сосудов и его применение.” читают:
Источник
Всем известно, что нужно сделать с чайником, чтобы из его носика полилась вода, – просто наклонить. А вот вопрос, можно ли перевести корабль через гору в море или другой водоем, вызовет у нас сомнение. Чтобы ответить на него, сначала следует узнать, что из себя представляют сообщающиеся сосуды.

Закон сообщающихся сосудов
Сообщающиеся сосуды – это взаимодействующие друг с другом сосуды, которые имеют общее дно.
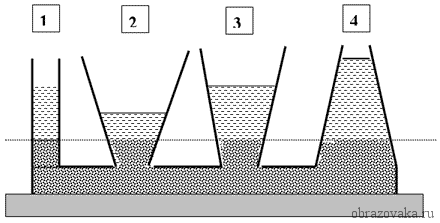
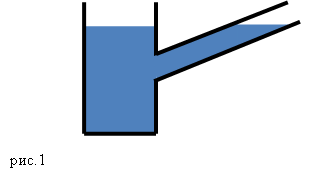
Рис. 1. Сообщающиеся сосуды
Закон сообщающихся сосудов гласит, что в таких сосудах, какую бы форму они не имели, поверхности однородных жидкостей в состоянии покоя находятся на одном уровне, то есть давление, оказываемое на стенки на любом горизонтальном уровне является одинаковым.
Если же в сосуде жидкости разные, то уровень выше в сосуде, в котором жидкость обладает меньшей плотностью. То есть, если в один сосуд налить жидкость, обладающую одной плотностью, а во второй – другой, то при равновесии их уровни не будут одинаковыми. Следовательно отсюда можно вывести формулу:
ρ1/ρ2=h2/h1
Где:
- ρ – плотность жидкости;
- h – высота столба.
Также для сообщающихся сосудов важной является формула:
p=gρh
Где:
- g – ускорение свободного падения;
- ρ – плотность жидкости (кг/куб.м);
- h – глубина (высота столба жидкости).
Этой формулой определяется давление жидкости на дно сосуда.
Древним римлянам было неизвестно определение сообщающихся сосудов, поэтому их акведуки – водопроводы занимали огромную протяженность над поверхностью земли и строились с равномерным уклоном вниз.
Свойства сообщающихся сосудов
В сообщающихся сосудах уровень жидкости одинаковый. Это происходит потому, что жидкость производит одинаковое давление на стенки сосуда. Достичь разного уровня однородной жидкости в сообщающихся сосудах можно с помощью перегородки между ними.
Перегородка перекроет сообщение между сосудами, и тогда можно в один из них долить жидкость, чтобы уровень изменился. В данной ситуации возникает напор – давление, производимое весом столба жидкости высотой, равной разности уровней. И если убрать перегородку, то именно это давление станет причиной тому, что жидкость будет перетекать в тот сосуд, где ее уровень ниже, до тех пор, пока уровни не станут одинаковыми.
В жизни очень часто можно встретить естественный напор. И таких примеров довольно много. Например, им обладает вода в горных реках, когда падает с высоты. Плотина также является примером естественного напора. Чем она выше, тем больше будет напор воды, поднятой плотиной.
Применение закона о сообщающихся сосудах
Принцип действия сообщающихся сосудов используется при сооружении фонтанов, водопроводов, шлюзов. Чайник и его носик тоже являются сообщающимися сосудами, так как вода, налитая в чайник, заполняет носик и всю остальную часть до одинаковой высоты. Применение свойств таких сосудов, могут даже помочь провести корабль через гору. И для этого как раз понадобиться шлюз. Шлюз – это лифт для судов. Если водное пространство перегорожено плотиной, то уровень воды в водохранилище выше, чем в реке ниже по течению. И чтобы добраться до этого уровня, судно должно зайти в шлюз, который отгорожен двумя водными непроницаемыми воротами. Когда шлюз полностью заполняется водой, судно выходит из шлюза и продолжает свой путь (уровень воды в шлюзе и водохранилище выравнивается по закону сообщающихся сосудов).

Рис. 2. Шлюз
Что мы узнали?
Из этой темы по физики за 7 класс можно ясно понять, какие сосуды называются сообщающимися. Ими могут называться лишь те сосуды, обладающие общим дном, где жидкость может свободно перетекать из одного сосуда в другой. Также сообщающиеся сосуды играют огромную роль в нашей повседневной жизни, облегчая ее и помогая выходить из трудных ситуаций. Принципы сообщающихся сосудов лежат в основе различных чайников, кофейников, водомерных стекол на паровых котлах.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
-
Полина Борисенко
9/10
Алика Квегмайр
10/10
Яна Василькова
10/10
Елена Куренкова
9/10
Мария Егорова
8/10
Тимофей Черный
10/10
Максим Скарнович
10/10
Люба Музыченко
10/10
Владимир Шитов
9/10
Константин Никитич
9/10
Оценка доклада
Средняя оценка: 4.2. Всего получено оценок: 850.
Источник
Определение
Соединенные между собой сосуды называют сообщающимися.
В таких сосудах жидкость имеет возможность перетекать из одной емкости в другую (рис.1). Форма сообщающихся сосудов может быть самая разная.
Допустим, что в сообщающиеся сосуды налита однородная жидкость, то в этих сосудах жидкость устанавливается на одном уровне, если давление над поверхностью жидкости одинаково, и не важно какую форму имеют сосуды. В неподвижной жидкости давление ($p$) на одном уровне в сообщающихся сосудах является равным, так как мы знаем, что:
[p=rho gh left(1right),]
где $rho $ – плотность жидкости; $g$ – ускорение свободного падения; $h$ – высота столба жидкости. Так как давление на одном уровне жидкости одинаково, то равными будут и высоты столбов жидкости.
Жидкости разной плотности в сообщающихся сосудах
Допустим, что в сообщающиеся сосуды налили жидкость разной плотности (рис.2(б)). В состоянии равновесия жидкостей, их уровни не будут находиться на одном уровне (высоты столбов жидкости равными не будут).
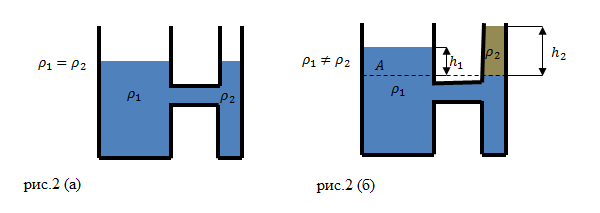
Жидкости в сосудах находятся в равновесии. Давления на уровне A (граница раздела разных жидкостей) (рис. 2 (б)) равны:
[{rho }_1gh_1={rho }_2gh_2left(2right),]
где ${rho }_1$ и ${rho }_2$ – плотности жидкостей. Найдем отношение высот столбов жидкостей в сосудах:
[frac{h_1}{h_2}=frac{{rho }_2}{{rho }_1}left(3right).]
Формула (3) говорит о том, что в сообщающихся сосудах высоты столбиков жидкости над уровнем их раздела обратно пропорциональны плотностям этих жидкостей. При одинаковом давлении над поверхностями жидкостей, высота столба жидкости с меньшей плотностью будет больше, чем высота столба более плотной жидкости.
Гидравлический пресс и другие примеры использования сообщающихся сосудов
В технике сообщающиеся сосуды используют часто. Например, существует такое устройство, как гидравлический пресс. Его изготавливают из двух цилиндров разного радиуса, в которых находятся поршни (рис.3). Сообщающиеся сосуды пресса обычно заполняют минеральным маслом.
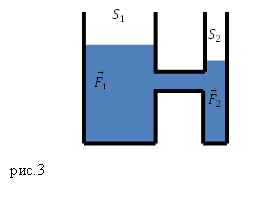
Пусть площадь первого поршня, к которому прикладывают силу ${overline{F}}_1,$ равна $S_1$, площадь второго $S_2$, к нему приложена сила ${overline{F}}_2$. Давление, которое создает первый поршень равно:
[p_1=frac{F_1}{S_1}left(4right).]
Второй поршень давит на жидкость:
[p_2=frac{F_2}{S_2}left(5right).]
Если система находится в состоянии равновесия, то по закону Паскаля давления $p_1$ и $p_2$ равны:
[frac{F_1}{S_1}=frac{F_2}{S_2}left(6right).]
Получим:
[F_1=F_2frac{S_1}{S_2}(7)]
величина первой силы больше модуля силы $F_2$ в $frac{S_1}{S_2}$ раз. Это означает, что при помощи гидравлического пресса, прикладывая небольшую силу к поршню малого сечения, можно получить большую по величине силу, которая будет действовать на большой поршень.
По принципу сообщающихся сосудов, в особенности раньше, действовал водопровод. Такой водопровод сейчас еще можно наблюдать на дачных участках. На относительно большой высоте устанавливается бак с водой, от бака идут водопроводные трубы, закрываемые кранами. Давление у кранов соответствует давлению столба воды, который равен разности высот уровень крана – уровень воды в баке.
Принципом сообщающихся сосудов пользовались, когда проектировали фонтаны, работающие без насосов, шлюзы на реках и каналах.
Примеры задач с решением
Пример 1
Задание. Имеются два цилиндрических сосуда. Высота столба жидкости в одном равна $h_1$, в другом $h_2$. Эти сосуды соединяют трубкой. Насколько изменится высота столба жидкости в левом сосуде, если площадь поперечного сечения его $S_1>S_2$ , $S_2$ – площадь сечения правого сосуда. Объемом трубки пренебречь.
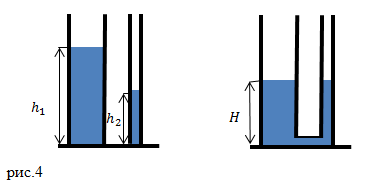
Решение. После того как сосуды соединили, они стали сообщающимися. Часть жидкости из левого сосуда перетечет в правый. Так как жидкость в правом и левом сосудах одна и та же, то уровни жидкости в обоих сосудах будут находиться на одном уровне, то есть высота столбиков жидкости станет равна $H$ в обоих коленах емкости. Определим, какой объем воды перетечет из левого колена в правое:
[Delta V_1=left(h_1-Hright)S_{1 }left(1.1right),]
где $S_{1 }$ – площадь поперечного сечения левого сосуда (сосуда из которого вытекает жидкость). В правом сосуде эта жидкость займет объем равный:
[Delta V_2=left(H-h_2right)S_{2 }left(1.2right),]
где $S_{2 }$ – площадь поперечного сечения правого сосуда. Так как мы считаем, что жидкость не сжимаема, то имеем:
[Delta V_1=Delta V_2left(1.3right).]
Приравниваем правые части выражений (1.2) и (1.1), выражаем высоту столбиков жидкости в правой и левой части сообщающихся сосудов:
[left(h_1-Hright)S_{1 }=left(H-h_2right)S_{2 }to H=frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }} left(1.4right).]
Используя выражение (1.4), изменение высоты жидкости в левом колене, получим равным:
[Delta h=h_1-H=h_1-frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }}=frac{h_1S_1+h_1S_2-h_1S_{1 }-S_{2 }h_2}{S_1+S_{2 }}=]
[=frac{h_1S_2-S_{2 }h_2}{S_1+S_{2 }}=frac{h_1-h_2}{S_1+S_{2 }}S_2.]
Ответ. $Delta h=frac{h_1-h_2}{S_1+S_{2 }}S_2$
Пример 2
Задание. Какой будет сила давления на большой поршень (площадью $S_1$) гидравлического пресса, если площадь его малого поршня равна $S_2$, при этом на него действует сила равная $F_2$?
Решение. В теоретическом разделе сказано, что гидравлический пресс представляет собой систему из сообщающихся сосудов (рис.3). Из закона Паскаля следует, что, прикладывая небольшую силу ($F_2$) к поршню малого сечения ($S_2$) пресса, можно получить большую по величине силу, которая будет действовать на большой поршень ($S_1$):
[F_1=F_2frac{S_1}{S_2}(2.1)]
Ответ. $F_1=F_2frac{S_1}{S_2}$
Читать дальше: условия плавания тел.
Источник
4.2. Элементы гидростатики
4.2.5. Сообщающиеся сосуды
Сообщающимися называются сосуды, соединенные между собой каналом, заполненным жидкостью.
Для сообщающихся сосудов справедлив закон сообщающихся сосудов: высоты взаимно уравновешенных столбов разнородных жидкостей обратно пропорциональны плотностям этих жидкостей:
h1h2=ρ2ρ1,
где h1 — высота столба жидкости плотностью ρ1; h2 — высота столба жидкости плотностью ρ2.
Указанный закон справедлив в отсутствие сил поверхностного натяжения.
Если сообщающиеся сосуды заполнены однородной жидкостью
ρ1 = ρ2,
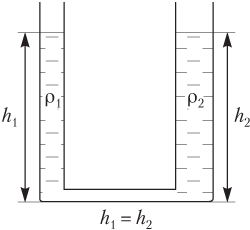
то свободные поверхности жидкости устанавливаются на одном уровне, независимо от формы сосудов (рис. 4.14):
h1 = h2,
где h1 — высота столба жидкости в левом колене; h2 — высота столба жидкости в правом колене сообщающихся сосудов.
Рис. 4.14
Если сообщающиеся сосуды заполнены разнородными жидкостями
ρ1 ≠ ρ2,
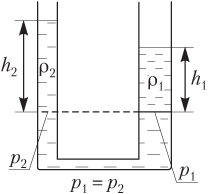
то свободные поверхности жидкостей, независимо от формы сосуда (рис. 4.15), устанавливаются так, что выполняется отношение
h1h2=ρ2ρ1,
где h1 — высота столба жидкости плотностью ρ1; h2 — высота столба жидкости плотностью ρ2.
Рис. 4.15
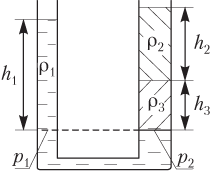
Если сообщающиеся сосуды заполнены несколькими жидкостями (например, как показано на рис. 4.16), то гидростатическое давление на одном уровне (отмеченном пунктиром) в левом колене определяется формулой
p1 = ρ1gh1,
в правом колене —
p2 = ρ2gh2 + ρ3gh3.
Рис. 4.16
Равенство давлений на указанном уровне
p1 = p2
позволяет записать тождество:
ρ1h1 = ρ2h2 + ρ3h3.
Пример 28. Два высоких сосуда, диаметр одного из которых в два раза больше диаметра второго, в нижней части соединены тонким шлангом. Площадь сечения узкого сосуда равна 10 см2. Система заполнена некоторым количеством жидкости плотностью 1,6 г/см3. Найти, на сколько миллиметров повысится уровень жидкости в каждом из сосудов, если в систему добавить 0,12 кг той же жидкости.
Решение. В сообщающихся сосудах однородная жидкость устанавливается на одном уровне.
Добавление в систему некоторого количества жидкости массой m приводит к ее распределению по двум сосудам в соответствии с площадью их поперечного сечения:
- в первом сосуде оказывается масса жидкости
m1 = ρV1 = ρ∆h1S1,
где ρ — плотность жидкости; V1 = S1∆h1 — объем жидкости в первом сосуде; S1 — площадь поперечного сечения первого сосуда; ∆h1 — повышение уровня жидкости в первом сосуде;
- во втором сосуде оказывается масса жидкости
m2 = ρV2 = ρ∆h2S2,
где V2 = S2∆h2 — объем жидкости во втором сосуде; S2 — площадь поперечного сечения второго сосуда; ∆h2 — повышение уровня жидкости во втором сосуде.
Повышение уровней жидкости в обоих сосудах одинаково:
∆h1 = ∆h2 = ∆h,
поэтому масса жидкости, добавленной в систему, определяется формулой
m = m1 + m2 = ρ∆h(S1 + S2).
Выразим отсюда искомое значение ∆h:
Δh=mρ(S1+S2).
Площади поперечного сечения сосудов связаны с их диаметрами формулой:
- для первого (широкого) сосуда
S1=πd124,
- для второго (узкого) сосуда
S2=πd224,
где d1 = 2d2 — диаметр первого (широкого) сосуда; d2 — диаметр второго (узкого) сосуда.
Отношение площадей
S1S2=πd1244πd22=d12d22=(d1d2)2=(2d2d2)2=4
позволяет найти площадь широкого сосуда:
S1 = 4S2.
Подставив S1 в формулу для ∆h
Δh=mρ(4S2+S2)=m5ρS2,
рассчитаем значение высоты, на которую повысится уровень жидкости в сосудах:
Δh=0,125⋅1,6⋅103⋅10⋅10−4=15⋅10−3 м=15 мм.
Пример 29. Два высоких сосуда, диаметр одного из которых в два раза больше диаметра другого, в нижней части соединены тонким шлангом. Площадь сечения широкого сосуда составляет 10 см2. Система заполнена жидкостью плотностью 6,0 г/см3. В узкий сосуд добавляют 0,12 кг жидкости плотностью 2,0 г/см3, а затем — 0,12 кг жидкости плотностью 4,0 г/см3. Найти разность уровней жидкостей в сосудах.
Решение. В сообщающихся сосудах неоднородная жидкость устанавливается на разных уровнях таким образом, что гидростатическое давление на выбранном уровне оказывается одинаковым:
p1 = p2,
где p1 — давление в широком сосуде; p2 — давление в узком сосуде.
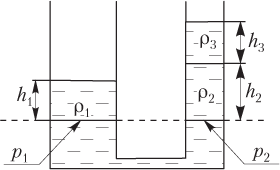
На рисунке пунктирной линией обозначен уровень, на котором будем рассчитывать гидростатическое давление в широком и узком сосудах.
Гидростатическое давление на выбранном уровне:
- в широком сосуде
p1 = ρ1gh1,
где ρ1 — плотность жидкости, заполняющей систему изначально; g — модуль ускорения свободного падения; h1 — высота столба жидкости в широком сосуде;
- в узком сосуде
p2 = ρ2gh2 + ρ3gh3,
где ρ2 — плотность первой жидкости, добавленной в узкий сосуд; h2 — высота столба первой жидкости; ρ3 — плотность второй жидкости, добавленной в узкий сосуд; h3 — высота столба второй жидкости.
Равенство давлений на указанном уровне
ρ1gh1 = ρ2gh2 + ρ3gh3
позволяет определить высоту столба жидкости в широком сосуде:
h1=1ρ1(ρ2h2+ρ3h3),
где высоты жидкостей h2 и h3 определяются соответствующими массами и плотностями:
- для первой жидкости
h2=m2ρ2S2;
- для второй жидкости
h3=m3ρ3S2,
где S2 — площадь поперечного сечения узкого сосуда; m2 — масса первой жидкости, добавленной в узкий сосуд; m3 — масса второй жидкости, добавленной в узкий сосуд.
Подстановка h2 и h3 в формулу для h1 дает
h1=1ρ1(ρ2m2ρ2S2+ρ3m3ρ3S2)=m2+m3ρ1S2.
Площади поперечного сечения сосудов связаны с их диаметрами формулой:
- для широкого сосуда
S1=πd124,
- для узкого сосуда
S2=πd224,
где d1 = 2d2 — диаметр широкого сосуда; d2 — диаметр узкого сосуда.
Отношение площадей
S1S2=πd1244πd22=d12d22=(d1d2)2=(2d2d2)2=4
позволяет найти площадь узкого сосуда:
S2=S14.
Таким образом, высота столба жидкости в широком сосуде определяется выражением
h1=4(m2+m3)ρ1S1.
Высота столба жидкости над указанным уровнем в узком сосуде есть сумма:
h2+h3=m2ρ2S2+m3ρ3S2=4S1(m2ρ2+m3ρ3).
Искомая разность верхних уровней жидкостей в узком (h2 + h3) и широком h1 сосудах рассчитывается по формуле
Δh=(h2+h3)−h1=4S1(m2ρ2+m3ρ3)−4(m2+m3)ρ1S1=
=4S1(m2ρ2+m3ρ3−(m2+m3)ρ1).
Произведем вычисление:
Δh=410⋅10−4(0,122,0⋅103+0,124,0⋅103−0,12+0,126,0⋅103)=0,20 м=20 см.
Источник