В сосуд с водой масса которой равна 600 а температура 10

1. На рисунке представлен график зависимости температуры t от времени τ для куска льда массой 480 г, помещённого при температуре −20 °С в калориметр. В тот же калориметр помещён нагреватель. Найдите, какую мощность развивал нагреватель при плавлении льда, считая эту мощность в течение всего процесса постоянной. Теплоёмкостью калориметра и нагревателя можно пренебречь. (Удельная теплота плавления льда — 330 кДж/кг.)
Решение.
Чтобы расплавить весь имеющийся лёд необходимо затратить энергию:
Здесь m — масса льда, λ — удельная теплота плавления льда.
Мощность нагревателя W — есть расход энергии в единицу времени. Время плавления определяем по графику:
Тогда, используя табличные данные и данные задачи, получаем:
Ответ: 330 Вт.
2. Сколько граммов воды можно нагреть на спиртовке на 30 °С, если сжечь в ней 21 грамм спирта? КПД спиртовки (с учётом потерь теплоты) равен 30 %. (Удельная теплота сгорания спирта 2,9·107Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг·°С)).
Решение.
При нагревании тела на температуру тело получает количество теплоты При сгорании тела выделяется энергия Учитывая, что КПД спиртовки равен 30 %, получаем:
Ответ: 1450 г.
3. Теплоизолированный сосуд содержит смесь льда и воды, находящуюся при температуре 0 °С. Масса льда 40 г, а масса воды 600 г. В сосуд впускают водяной пар при температуре +100 °С. Найдите массу впущенного пара, если известно, что окончательная температура, установившаяся в сосуде, равна +20 °С.
Решение.
Окончательная температура положительна, значит, весь лед расплавился, и вся получившаяся вода нагрелась.
При этом пар конденсировался и полученная вода остыла. С учетом этого запишем уравнение теплового баланса:
и выразим отсюда массу пара:
Здесь Qпол и Qотд — полученная и отданная теплота соответственно, m1, m2, m3 — массы льда, воды, пара соответственно, λ — удельная теплота плавления льда, c — удельная теплоемкость воды, τ — удельная теплота парообразования, t2 — конечная температура, t1 — исходная температура смеси лед-вода, t3 — температура пара.
Переведя граммы в килограммы и подставляя данные задачи и табличные данные, получаем:
Ответ: 25,4 г.
4. Литровую кастрюлю, полностью заполненную водой, из комнаты вынесли на мороз. Зависимость температуры воды от времени представлена на рисунке. Какое количество теплоты выделилось при кристаллизации и охлаждении льда?
Примечание.
Удельную теплоту плавления льда считать равной
Решение.
Поскольку объём воды равен одному литру, масса воды равна одному килограмму. Таким образом, кристаллизовался 1 кг льда, выделив при этом
Также тепло выделялось при охлаждении льда:
Следовательно, при кристаллизации и охлаждении льда выделилось 372 кДж энергии.
Ответ: 372 кДж.
5. Сколько граммов спирта нужно сжечь в спиртовке, чтобы нагреть на ней воду массой 580 г на 80 °С? КПД спиртовки (с учётом потерь теплоты) равен 20%. (Удельная теплота сгорания спирта 2,9·107Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг·°С)).
Решение.
При нагревании тела на температуру тело получает количество теплоты При сгорании тела выделяется энергия Учитывая, что КПД спиртовки равен 20%, получаем:
Ответ: 33,6 г.
6. Какое количество теплоты выделится при кристаллизации 2 кг расплавленного олова, взятого при температуре кристаллизации, и последующем его охлаждении до 32 °С? (Удельная теплоёмкость олова — 230 Дж/(кг · °С).)
7. Тонкостенный сосуд содержит смесь льда и воды, находящуюся при температуре 0 °С. Масса льда 350 г, а масса воды 550 г. Сосуд начинают нагревать на горелке мощностью 1,5 кВт. Сколько времени понадобится, чтобы довести содержимое сосуда до кипения? Потерями теплоты и удельной теплоёмкостью сосуда, а также испарением воды можно пренебречь.
Решение.
Чтобы довести содержимое сосуда до кипения за время τ, необходимо расплавить лёд, а затем нагреть всю получившуюся воду до температуры кипения, следовательно, затратить энергию, равную
Здесь m1, m2, — массы льда и воды соответственно, λ — удельная теплота плавления льда, c — удельная теплоёмкость воды, t2 — температура кипения воды, t1 — исходная температура смеси лед-вода.
Мощность горелки W есть расход энергии в единицу времени, откуда находим τ:
Подставляя табличные данные и данные задачи, находим:
Ответ: 5,5 мин.
8. На рисунке представлен график зависимости температуры от полученного количества теплоты для вещества массой 1 кг. Первоначально вещество находилось в твёрдом состоянии. Определите удельную теплоёмкость вещества в твёрдом состоянии.
Решение.
Удельная теплоёмкость — это количество теплоты, необходимое для того, чтобы нагреть вещество на 1 °C. Из графика видно, что для нагревания 1 кг вещества на 200 °C потребовалось 50 кДж. Таким образом, удельная теплоёмкость равна:
Ответ:
9. В тонкостенный сосуд налили воду, поставили его на электрическую плитку мощностью 800 Вт и начали нагревать. На рисунке представлен график зависимости температуры воды t от времени τ. Найдите массу налитой в сосуд воды. Потерями теплоты и теплоёмкостью сосуда пренебречь.
10. Какое количество теплоты потребуется, чтобы в алюминиевом чайнике массой 700 г вскипятить 2 кг воды? Первоначально чайник с водой имели температуру 20 °С.
Примечание.
Удельную теплоёмкость алюминия считать равной
Решение.
Для нагревания чайника необходимо
Для нагревания воды:
Всего потребуется
Ответ: 723,52 кДж.
11. Какое количество теплоты выделится при конденсации 2 кг пара, взятого при температуре кипения, и последующего охлаждения воды до 40 °С при нормальном атмосферном давлении?
Решение.
В данном случае тепло отдавали пар и получившаяся из него вода. Пар отдал:
вода отдала:
Таким образом:
Ответ: 5104 кДж.
12. Какое минимальное количество теплоты необходимо для превращения в воду 500 г льда, взятого при температуре −10 °С? Потерями энергии на нагревание окружающего воздуха пренебречь.
Решение.
Для нагревания льда до температуры плавления необходимо:
Для превращения льда в воду:
Таким образом:
Ответ: 175 500 Дж.
13. В сосуд с водой положили кусок льда. Каково отношение массы льда к массе воды, если весь лёд растаял и в сосуде установилась температура 0 °С? Теплообменом с окружающим воздухом пренебречь. Начальные температуры воды и льда определите из графика зависимости температуры t от времени τ для воды и льда в процессе теплообмена.
Решение.
Лёд растает за счёт того, что вода будет остывать и тем самым отдавать своё тепло. Запишем это в формульном виде: где — теплоёмкость воды, — удельная теплота плавления льда, — масса воды и льда соответственно.
Таким образом,
Ответ: 0,42.
14. Как изменится внутренняя энергия 500 г воды, взятой при 20°С, при её превращении в лёд при температуре 0 °С?
Решение.
При охлаждении воды до 0 °С выделится количество теплоты, равное:
Затем при кристаллизации воды выделится количество теплоты, равное:
Таким образом, всего вода отдаст теплоты.
Ответ: 207 кДж.
15. В стакан массой 100 г, долго стоявший на улице, налили 200 г воды из лужи при температуре +10 °С и опустили в неё кипятильник. Через 5 минут работы кипятильника вода в стакане закипела. Пренебрегая потерями теплоты в окружающую среду, найдите мощность кипятильника. Удельная теплоёмкость материала стакана равна 600 Дж/(кг · °С).
16. Два однородных кубика привели в тепловой контакт друг с другом (см. рисунок). Первый кубик изготовлен из цинка, длина его ребра 2 см, а начальная температура t1 = 1 °C. Второй кубик изготовлен из меди, длина его ребра 3 см, а начальная температура t2 = 74,2 °C. Пренебрегая теплообменом кубиков с окружающей средой, найдите температуру кубиков после установления теплового равновесия.
Примечание.
Плотности цинка и меди соответственно:
Удельные теплоёмкости цинка и меди соответственно:
Решение.
При нагревании(охлаждении) тела на температуру тело получает(отдаёт) количество теплоты Более горячее тело передаёт тепло более холодному, запишем уравнение теплового баланса: Заметим, что теплоёмкости цинка и меди равны, поэтому их можно сократить. Раскроем скобки:
Найдём массы кубиков:
Подставим эти значения в формулу для конечной температуры:
Ответ:
17. Сколько литров воды при 83 °С нужно добавить к 4 л воды при 20 °С, чтобы получить воду температурой 65 °С? Теплообменом с окружающей средой пренебречь.
Решение.
Плотность воды равна 1 кг/л, теплоемкость равна 4 200 Дж/кг. Таким образом, изначально мы имеем m0 = 4 кг воды при температуре t0 = 20 °C. Добавляется некоторое количество воды массой m1 при температуре t1 = 83 °C. Конечная температура смеси равна tкон, а её масса m0 + m1.
Составим уравнение теплового баланса для процесса:
— отданное в процессе тепло;
— полученное в процессе тепло;
.
Таким образом,
следовательно, необходимо 10 л воды.
Ответ: 10.
18. В тонкостенный сосуд налили воду массой 1 кг, поставили его на электрическую плитку и начали нагревать. На рисунке представлен график зависимости температуры воды t от времени τ. Найдите мощность плитки. Потерями теплоты и теплоёмкостью сосуда пренебречь.
Решение.
Мощность, это отношение теплоты ко времени, за которую эта теплота получена Теплота, полученная телом при нагревании на температуру рассчитывается по формуле Используя график, найдём мощность плитки:
Ответ: 700 Вт.
19. 3 л воды, взятой при температуре 20 °С, смешали с водой при температуре 100 °С. Температура смеси оказалась равной 40 °С. Чему равна масса горячей воды? Теплообменом с окружающей средой пренебречь.
Решение.
Более холодная вода нагрелась за счет остывания горячей воды: . Масса воды вычисляется по формуле:
Выражаем массу горячей воды:
Ответ: 1.
20. Килограммовый кусок льда внесли с мороза в тёплое помещение. Зависимость температуры льда от времени представлена на рисунке. Какое количество теплоты было получено в интервале времени от 50 мин до 60 мин?
Решение.
Исходя из графика, в интервале от 50 до 60 минут происходил нагрев воды от 0 °C до 20 °C. Вычислим количество теплоты:
Ответ: 84 кДж.
21. В стакан массой 100 г, долго стоявший на столе в комнате, налили 200 г воды при комнатной температуре +20 °С и опустили в неё кипятильник мощностью 300 Вт. Через 4 минуты работы кипятильника вода в стакане закипела. Пренебрегая потерями теплоты в окружающую среду, найдите удельную теплоёмкость материала стакана.
22. Два однородных кубика привели в тепловой контакт друг с другом. Первый кубик изготовлен из меди, длина его ребра 3 см, а начальная температура t1 = 2 °C. Второй кубик изготовлен из алюминия, длина его ребра 4 см, а начальная температура t2 = 74 °C. Пренебрегая теплообменом кубиков с окружающей средой, найдите температуру кубиков после установления теплового равновесия.
Примечание.
Плотности алюминия и меди соответственно:
Удельные теплоёмкости алюминия и меди соответственно:
Решение.
При нагревании(охлаждении) тела на температуру тело получает(отдаёт) количество теплоты Более горячее тело передаёт тепло более холодному, запишем уравнение теплового баланса: Раскроем скобки:
Найдём массы кубиков:
Подставим эти значения в формулу для конечной температуры:
Ответ:
23. Двигатель трактора совершил полезную работу 23 МДж, израсходовав при этом 2 кг бензина. Найдите КПД двигателя трактора.
Решение.
При сгорании 2 кг бензина выделяется теплоты, где — удельная теплота сгорания бензина. КПД рассчитывается по формуле:
Ответ: 25 %.
24. Автомобиль УАЗ израсходовал 30 кг бензина за 2 ч. езды. Чему равна мощность двигателя автомобиля, если его КПД составляет 30%? (Удельная теплота сгорания бензина 4,6·107Дж/кг).
Решение.
Энергия, полученная двигателем от 30 кг бензина КПД определяется как отношение полезной работы к энергии, потребляемой двигателем Мощность двигателя — это отношение полезной работы совершаемой двигателем ко времени:
Ответ: 57,5 кВт.
25. В сосуд с водой положили кусок льда. Каково отношение массы воды к массе льда, если весь лёд растаял и в сосуде установилась температура 0 °С? Теплообменом с окружающим воздухом пренебречь. Начальную температуру воды и льда определите из графика зависимости от времени для воды и льда в процессе теплообмена.
Решение.
Лед растает за счёт того, что вода будет остывать и тем самым отдавать своё тепло. Запишем это в формульном виде: где — удельная теплоёмкость воды, — удельная теплота плавления льда, — масса воды и льда соответственно.
Таким образом,
Ответ: 2,38.
Источник
Задачи на количество теплоты с решениями
Формулы, используемые на уроках «Задачи на количество теплоты,
удельную теплоемкость».
1 г = 0,001 кг; 1 т = 1000 кг; 1 кДж = 1000 Дж; 1 МДж = 1000000 Дж
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?
При решении задачи нужно учесть, что оба тела — и котёл, и вода — будут нагреваться вместе. Между ними происходит теплообмен. Их температуры можно считать одинаковыми, т. е. температура котла и воды изменяется на 100 °С — 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми. Ведь их массы и удельные теплоёмкости различны.

Задача № 2.
Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.

Задача № 3.
Стальная деталь массой 3 кг нагрелась от 25 до 45 °С. Какое количество теплоты было израсходовано?

Задача № 4.
В сосуде содержится 3 л воды при температуре 20 °С. Сколько воды при температуре 45 °С надо добавить в сосуд, чтобы в нём установилась температура 30 °С? Необходимый свободный объём в сосуде имеется. Теплообменом с окружающей средой пренебречь

Задача № 5.
На сколько градусов изменилась температура чугунной детали массой 12 кг, если при остывании она отдала 648000 Дж теплоты?

Задача № 6.
По графику определите удельную теплоёмкость образца, если его масса 50 г.
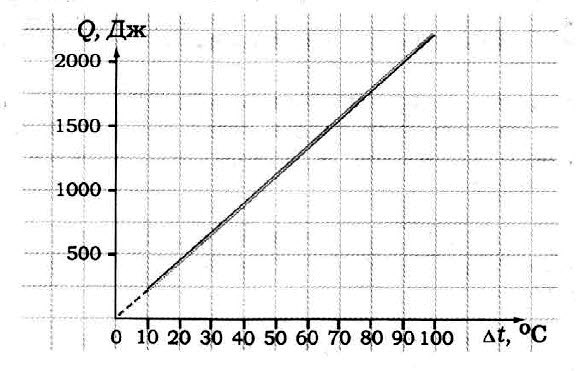

Задача № 7.
Для нагревания медного бруска массой 3 кг от 20 до 30 °С потребовалось 12000 Дж теплоты. Какова удельная теплоемкость меди?

Задача № 8.
Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей 2,1 кДж энергии. Чему равна удельная теплоемкость камня?
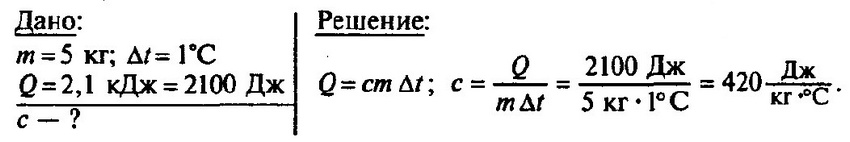
Задача № 9.
Какое количество теплоты потребуется для нагревания на 1 °С воды объемом 0,5 л; олова массой 500 г; серебра объемом 2 см3; стали объемом 0,5 м3; латуни массой 0,2 т?

Задача № 10.
Какое количество теплоты получили алюминиевая кастрюля массой 200 г и находящаяся в ней вода объемом 1,5 л при нагревании от 20 °С до кипения при температуре 100 °С?

Задача № 11.
а) Воздух, заполняющий объем 0,5 л в цилиндре с легким поршнем, нагрели от 0 до 30 °С при постоянном атмосферном давлении. Какое количество теплоты получил воздух?
б) В порожнем закрытом металлическом баке вместимостью 60 м3 под действием солнечного излучения воздух нагрелся от 0 до 20 °С. Как и на сколько изменилась внутренняя энергия воздуха в баке? (Удельная теплоемкость воздуха при постоянном объеме равна 720 Дж/кг-°С.)

Задача № 12.
ОГЭ
Металлический цилиндр массой m = 60 г нагрели в кипятке до температуры t = 100 °С и опустили в воду, масса которой mв = 300 г, а температура tв = 24 °С. Температура воды и цилиндра стала равной Θ = 27 °С. Найти удельную теплоёмкость металла, из которого изготовлен цилиндр. Удельная теплоёмкость воды св = 4200 Дж/(кг К).

Задача № 13.
В теплоизолированном сосуде сначала смешивают три порции воды 100 г, 200 г и 300 г с начальными температурами 20 °C, 70 °C и 50 °C соответственно. После установления теплового равновесия в сосуд добавляют новую порцию воды массой 400 г при температуре 20 °C. Определите конечную температуру в сосуде. Ответ дайте в °C, округлив до целого числа. Теплоёмкостью калориметра пренебрегите.
Решение.

Ответ: 39 °С.
Задача № 14. (повышенной сложности)
Стальной шарик радиусом 5 см, нагретый до температуры 500 ˚С, положили на лед, температура которого 0 ˚С. На какую глубину погрузится шарик в лед? (Считать, что шарик погрузился в лед полностью. Теплопроводностью шарика и нагреванием воды пренебречь.)
Дано: R = 0,05 м; t1 = 500 ˚С; t2 = 0 ˚С;
ρ1 (плотность стали) = 7800 кг/м3.;
ρ2 (плотность льда) = 900 кг/м3.
c (удельная теплоемкость стали) = 460 Дж/кг •˚С,
λ (удельная теплота плавления льда) = 3,3 • 105 Дж/кг,
Найти: h – ?

Краткая теория для решения Задачи на количество теплоты.

Конспект урока «Задачи на количество теплоты».
Посмотреть конспект урока по теме «Количество теплоты. Удельная теплоемкость»
Следующая тема: «ЗАДАЧИ на сгорание топлива с решениями».
Источник
Сохраните:
Задания и ответы для Московской олимпиады школьников (МОШ) по физике 7,8,9,10,11 класс первого тура отборочного этапа 2020-2021 ученый год, официальная дата проведения олимпиады: 16.10.2020-18.10.2020 (с 16 по 18 октября 2020 года).
Ссылка для скачивания заданий для 7 класса: скачать в PDF
Ссылка для скачивания заданий для 8 класса: скачать в PDF
Ссылка для скачивания заданий для 9 класса: скачать в PDF
Ссылка для скачивания заданий для 10 класса: скачать в PDF
Ссылка для скачивания заданий для 11 класса: скачать в PDF
P.S свои ответы предлагайте ниже в комментариях, помогите друг другу.
Московская олимпиада школьников по физике 7 класс первый тур отборочного этапа 2020-2021 задания и ответы:
1)Для определения скорости игрушечного поезда, который работает на батарейках, достаточно иметь… 1) Весы; 2) мензурку; 3) линейку; 4) часы; 5) микрометр; 6) ареометр.
2)Переведите в СИ: 150 000 мг (миллиграмм).
3)Цена деления мензурки, изображённой на рисунке, равна.
4)В мензурках находится вода. Какой объём воды будет в первой мензурке, если в неё перелить пятую часть воды из второй мензурки и половину воды из третьей мензурки?
5)Три шестёренки зацеплены зубьями между собой, как показано на рисунке, и могут вращаться вокруг закрепленных осей. Куда вращается нижняя («образование») шестеренка, если верхняя («успех») вращается по часовой стрелке?
Сколько оборотов в день делает нижняя шестерня («образование»), если известно, что верхняя («успех») делает 28 оборотов в неделю?
6)Из пункта А почтальон Печкин выехал на велосипеде в 12:00, направляясь в пункт Б. Одновременно с ним из пункта Б выехал на самокате дядя Фёдор, направляясь в пункт А. Впоследствии почтальон Печкин рассказывал, что в 12:30 встретил дядю Фёдора. Дядя Фёдор же вспоминал, что прибыл в пункт А в 13:15. Что показывали часы почтальона Печкина, когда он добрался до пункта Б? Считайте, что почтальон Печкин и дядя Фёдор двигались с постоянными скоростями. В качестве ответа запишите отдельно два числа – число часов (от 0 до 23) и целое число минут (от 0 до 59).
7)Дядя Вася хочет полностью наполнить две стоящие рядом бочки водой, не пролив её на землю. Он кладёт шланг в меньшую бочку, идёт к крану, открывает его и возвращается назад. После возвращения он ждёт 15 секунд, пока бочка заполнится, и перекладывает шланг в другую бочку. Подождав еще 2 минуты, дядя Вася возвращается к крану и закрывает его. Чему равно расстояние от бочек до крана, если дядя Вася ходит со скоростью 1 м/с, а вторая бочка по объёму вчетверо больше первой? Ответ выразите в м, округлите до целого числа.
8)Левая шкала измеряет объём жидкости в миллилитрах (ml), правая в – «чашках» (cup).
Чему равна цена деления левой шкалы? Ответ выразите в мл, округлите до целого числа.
Чему равна цена деления правой шкалы? Ответ выразите в «чашках», округлите до тысячных.
Найдите, чему равно расстояние между двумя ближайшими рисками на правой шкале, если на левой оно равно 1 см. Ответ выразите в мм, округлите до десятых.
Московская олимпиада школьников по физике 8 класс первый тур отборочного этапа 2020-2021 задания и ответы:
1)Переведите в СИ: 321 л, 1 день
2)Таракан ползёт по прямой. Первые 10 с его скорость постоянна и равна 20 см/с, следующие 20 с его скорость составляет 16 см/с, затем он 10 с стоит на месте. Остаток пути он ползёт с постоянной скоростью 13 см/с. Найти среднюю скорость таракана на всем пути.
3)В каком случае перевозить камень на тачке удобнее?
4)К пружине, жёсткость которой k=100 Н/м, прикрепили грузик. Пружина удлинилась на Δx1=5 см. Если грузик погрузить в жидкость, удлинение пружины станет равным Δx2=2 см. Какая сила Архимеда действует на грузик в жидкости?
5)Однородные шарики покоятся на рычажных весах, как показано на рисунке. Плотность какого из шаров наименьшая? V2>V1=V3.
6)Кеша и Тучка, находясь в своих домиках, получили одновременно СМС-ки от Лисички с информацией, что яблочный пирог уже готов, и тут же бросились бежать к дому Лисички. Кеша половину времени бежал со скоростью 5 м/с, а оставшуюся половину времени со скоростью 4 м/с (устал). Тучка первую половину пути пробежал со скоростью 4 м/с, а вторую половину пути со скоростью 5 м/с. В результате оба прибежали к Лисичке одновременно. Каково расстояние от дома Кеши до дома Лисички в шагах Цыпы, если расстояние от дома Тучки до дома Лисички равно 800 шагов Цыпы?
7)Атос и Портос начинают одновременно идти навстречу друг другу со скоростями v1=3 м/с и v2=1 м/c соответственно. Арамис сначала находится посередине между ними. Портос встретился с Арамисом через t1=250 с после начала своего движения, а с Атосом через t2=12 мин.
На каком расстоянии друг от друга первоначально находились Атос и Портос? Ответ выразите в м, округлите до целого числа.
Насколько позже стартовал Арамис, если скорость сближения Портоса с Арамисом в 2 раза больше скорости удаления Арамиса от Атоса? Ответ выразите в с, округлите до целого числа.
8)На тарелке лежит торт, состоящий из трёх слоёв. Эти слои имеют высоту h1=15 мм, h2=25 мм и h3=20 мм, а их плотности соответственно равны ρ1=600 кг/м3, ρ2=460 кг/м3 и ρ3=400 кг/м3. Чему равна средняя плотность всего торта? Ответ выразите в кг/м3, округлите до целого числа.
9)В двух сообщающихся сосудах, имеющих форму цилиндров c площадью дна S1=100 см2 и S2=200 см2, находится вода. Сосуды закрыты сверху массивными поршнями (см. рисунок).
К правому поршню прикреплена легкая вертикальная пружина жёсткостью k=4 Н/см , верхний конец которой неподвижен. Система находится в равновесии, причём пружина изначально сжата. На левый поршень положили груз массой m=1 кг. Плотность воды ρ=1000 кг/м3, ускорение свободного падения g=10 Н/кг. Начальная высота края правого сосуда над поверхностью воды h=10 см.
Найдите, на сколько после этого опустится левый поршень. Ответ выразите в см, округлите до целого числа.
Груз какой минимальной массы нужно добавить к грузу массой m (на левый поршень) для того, чтобы вода начала выливаться из правого сосуда? Ответ выразите в кг, округлите до целого числа.
10)Система состоит из невесомых блоков, трёх грузов массой m=1 кг каждый, двух грузов массой mx каждый и невесомых нитей. Ускорение свободного падения g=10 Н/кг.
Чему равна величина mx, если система находится в равновесии? Ответ выразите в кг, округлите до десятых.
C какой силой действует система на потолок? Ответ выразите в Н, округлите до целого числа.
Московская олимпиада школьников по физике 9 класс первый тур отборочного этапа 2020-2021 задания и ответы:
1)Улитка ползёт по прямой. Первый час её скорость постоянна и равна 1,2 см/с, еще два часа её скорость составляет 0,8 см/с, затем она ровно час отдыхала неподвижно. Остаток пути она ползла с постоянной скоростью 0,7 см/с. Найти среднюю скорость улитки на всем пути.
2)В сосуде с водой плавают два шара с радиусами 2R и R, как показано на рисунке. Чему равна плотность первого шара?
3)Система из двух блоков, двух грузов и обезьянки, находится в равновесии. Определите массу тела m1, если масса второго груза равна 2m, а масса обезьяны – m. Нити и блоки невесомые, трения нет.
4)В трёх кастрюлях находится вода. В первой кастрюле вода только закипела, во второй кипит 3 минуты, в третьей кипит 10 минут. В какой из кастрюль температура воды наибольшая?
5)Сто резисторов с сопротивлениями 1 Ом, 3 Ом, 5 Ом, … , 197 Ом, 199 Ом соединили параллельно. Эквивалентное сопротивление…
6)Рассмотрим объединение двух однополосных дорог A и B в однополосную дорогу C. В часы пик все три дороги заполнены автомобилями. Среднее расстояние между двумя соседними автомобилями можно считать одинаковым на всех трёх дорогах. Длина дороги A равна LA=1 км, дороги B: LB=3 км, а дороги C: LC=2 км. Средняя скорость автомобилей на дороге A составляет vA=3 км/ч, а среднее время, за которое машины проезжают дорогу B, равно tB=36 мин. За какое время в среднем автомобиль добирается от начала дороги A до конца дороги C? Ответ выразите в минутах, округлите до целого числа.
7)К невесомой системе, состоящей из нерастяжимых ниток, двух блоков и трёх пружин с коэффициентами жёсткости k и 2k, прикрепляют груз массой m=600 г, как показано на рисунке. k=50 Н/м, ускорение свободного падения равно 10 м/c2.
На какое расстояние опустится груз, когда система придёт в равновесие? Ответ выразите в см, округлите до десятых.
С какой силой система действует на потолок в положении равновесия? Ответ выразите в Н, округлите до целого числа.
8)Г-образный сосуд, наполненный ртутью и керосином, стоит на столе, как показано на рисунке. Силы давления жидкостей (без учета атмосферного давления) на горизонтальные стенки сосуда AB и CD, перпендикулярные плоскости рисунка, равны 40 Н и 8 Н соответственно. Известно, что при малейшем добавлении керосина в сосуд, он опрокидывается. Найдите отношение высоты столба ртути к высоте столба керосина. Ответ округлите до десятых. Плотность керосина 800 кг/м3, плотность ртути 13600 кг/м3.
9)Электрическая схема изменяет мощность W электрического нагревателя по линейному закону от времени t, прошедшего после включения нагревателя: W(t)=W0∙t/τ. W0=100 Вт, τ=10 секунд. Этот нагреватель помещён на дно банки с 1 литром воды в ней. Начальная температура воды 20°С. Пренебрегая теплоёмкостью банки и потерями теплоты в окружающую среду, найдите, какой стала температура воды в банке через 3 минуты после включения нагревателя? Удельная теплоёмкость воды 4,2 Дж/(г∙℃). Ответ выразите в градусах по шкале Цельсия, округлите до десятых.
10)Электрическая цепь состоит из идеальной батарейки с напряжением 3,2 В, резистора, идеального амперметра и двух вольтметров. Первый вольтметр показывает 1 В, а второй 2 В. Показание амперметра 1 мкА.
Чему равно сопротивление первого вольтметра? ?
