В сосуд с водой массой 250 г при температуре 18

Условие задачи:
В сосуд с водой объемом 0,25 л при 20 °C поместили 50 г расплавленного свинца с температурой 400 °C. Какая температура установится в результате теплообмена в сосуде? Удельные теплоёмкости расплава и твердого свинца считать одинаковыми.
Задача №5.2.30 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(V_1=0,25) л, (t_1=20^circ) C, (m_2=50) г, (t_2=400^circ) C, (t-?)
Решение задачи:
В этой задаче нужно обязательно произвести оценку. Давайте для начала определим количество теплоты (Q_1), которое необходимо для нагревания воды массой (m_1) от температуры (t_1) до температуры кипения (t_к) ((t_к=100^circ) C). Это можно сделать по следующей формуле:
[{Q_1} = {c_1}{m_1}left( {{t_к} – {t_1}} right)]
Удельная теплоёмкость воды (c_1) равна 4200 Дж/(кг·°C).
Массу (m_1) представим как произведение плотности воды (rho) (она равна 1000 кг/м3) на объем (V_1), тогда:
[{Q_1} = {c_1}rho {V_1}left( {{t_к} – {t_1}} right)]
Посчитаем численное значение (Q_1) (объем при расчете мы перевели в кубические метры):
[{Q_1} = 4200 cdot 1000 cdot 0,25 cdot {10^{ – 3}} cdot left( {100 – 20} right) = 84000;Дж]
Так как температура расплавленного свинца (t_2) больше температуры его плавления (t_п) ((t_п=327^circ) C), то определим количество теплоты (Q_2), выделяемое при охлаждении расплава свинца от температуры (t_2) до температуры (t_п).
[{Q_2} = {c_2}{m_2}left( {{t_2} – {t_п}} right)]
Удельная теплоёмкость расплава свинца (и твёрдого свинца) (c_2) равна 130 Дж/(кг·°C).
[{Q_2} = 130 cdot 0,05 cdot left( {400 – 327} right) = 474,5;Дж]
Количество теплоты (Q_3), выделяемое при кристаллизации свинца массой (m_2), определим по формуле:
[{Q_3} = lambda {m_2}]
Удельная теплота кристаллизации (плавления) свинца (lambda) равна 25 кДж/кг.
[{Q_3} = 25 cdot {10^3} cdot 0,05 = 1250;Дж]
Количество теплоты (Q_4), выделяемое при охлаждении свинца массой (m_2) от температуры (t_п) до температуры (t_к), равно:
[{Q_4} = {c_2}{m_2}left( {{t_п} – {t_к}} right)]
[{Q_4} = 130 cdot 0,05 cdot left( {327 – 100} right) = 1475,5;Дж]
Видно, что ({Q_1} > {Q_2} + {Q_3} + {Q_4}), значит температура теплового равновесия будет лежать в пределах от (t_1) до (t_к). Запишем уравнение теплового баланса:
[{Q_5} = {Q_2} + {Q_3} + {Q_6}]
Здесь (Q_5) – количество теплоты, необходимое для нагревания воды массой (m_1) от температуры (t_1) до температуры (t); (Q_6) – количество теплоты, выделяемое при охлаждении свинца массой (m_2) от температуры (t_п) до температуры (t). Тогда:
[{c_1}{m_1}left( {t – {t_1}} right) = {c_2}{m_2}left( {{t_2} – {t_п}} right) + lambda {m_2} + {c_2}{m_2}left( {{t_п} – t} right)]
[{c_1}{m_1}left( {t – {t_1}} right) = {c_2}{m_2}left( {{t_2} – t} right) + lambda {m_2}]
Раскроем скобки:
[{c_1}{m_1}t – {c_1}{m_1}{t_1} = {c_2}{m_2}{t_2} – {c_2}{m_2}t + lambda {m_2}]
Все члены с множителем (t) перенесем в левую сторону, вынесем его за скобки, остальные перенесем в правую.
[tleft( {{c_1}{m_1} + {c_2}{m_2}} right) = {c_1}{m_1}{t_1} + {c_2}{m_2}{t_2} + lambda {m_2}]
[t = frac{{{c_1}{m_1}{t_1} + {c_2}{m_2}{t_2} + lambda {m_2}}}{{{c_1}{m_1} + {c_2}{m_2}}}]
Массу (m_1) представим как произведение плотности воды (rho) на объем (V_1), как это уже было сделано выше:
[t = frac{{{c_1}rho {V_1}{t_1} + {c_2}{m_2}{t_2} + lambda {m_2}}}{{{c_1}rho {V_1} + {c_2}{m_2}}}]
Переведём некоторые величины в систему СИ:
[0,25;л = 0,25 cdot {10^{ – 3}};м^3]
[50;г = 0,05;кг]
Численно температура (t) равна:
[t = frac{{4200 cdot 1000 cdot 0,25 cdot {{10}^{ – 3}} cdot 20 + 130 cdot 0,05 cdot 400 + 25 cdot {{10}^3} cdot 0,05}}{{4200 cdot 1000 cdot 0,25 cdot {{10}^{ – 3}} + 130 cdot 0,05}} = 23,5^circ;C = 296,5;К]
Ответ: 296,5 К.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Источник

Решебник по физике
заполнены газом, причем в одной из них давление в n раз больше, чем в другой. Перегородки удерживают неподвижно. На какое расстояние h передвинется перегородка, если ее отпустить?
Ответ: h = H((n−1)) . 2 n+1
Задача 22. Сколько времени требуется, чтобы камеру автомобильной шины объемом V накачать до давления p, если при каждом качании насос захватывает из атмосферы цилиндрический столб воздуха высотой h и диаметром d, а время одного качания t1? Начальное давление в камере p1.
4Vt1 | p | |
Ответ: t = | −1 . | |
2 | ||
πd h p1 | ||
Задача23. На сколько градусов надо нагреть газ, чтобы он, изобарно расширившись, увеличил объем на 30 %, если до нагревания его температура была t1° = 27 °С?
Ответ: ∆T = 0,3Т1 = 87 K.
Задача 24. Температура воздуха в цилиндре t1°= 17 °С (рис. 88). После нагревания на ∆T = 30 K поршень переместился на ∆l = 5 см. Какой объем V2 займет воздух после нагревания? Площадь поршня S = = 10 см2. Процесс изобарный.
T | =5,5 10−4 | |||
Ответ: V = ∆lS | 1 | +1 | м3. | |
∆T | ||||
2 | ||||
Рис. 88
Задача25.На рис. 89 изображен некоторый замкнутый круговой процесс (цикл) в координатных осях V — T, происходящий с одной и той же массой идеального газа. Изобразите этот цикл в координатных осях p — V и p — T.
Задача26. Как изменяется давление данной массы идеального газа при переходе из состояния 1 в состояние 2 (рис. 90)?
260

2. Молекулярная физика и термодинамика | |
Рис. 89 | Рис. 90 |
Задача 27. В комнате объемом V = 50 м3 находится воздух с относительной влажностью ϕ= 60 % при температуре t° = 20 °С. Найти число молекул водяного пара в комнате. Плотность насыщенного водяного пара при 20 °С равна
17,3 г/м3.
Ответ: N = ϕpн=acVNA = 2 1025.
RT100%
Задача28.Какова внутренняя энергия идеального одноатомного газа U, занимающего объем V при температуре Т, если концентрация его молекул n?
Ответ: U = 32knTV .
Задача 29. Найти изменение внутренней энергии ∆U воды массой m = 1 кг, взятой при t1° = 0 °С, при превращении ее в пар с температурой t2°= 100 °С? Удельная теплоемкость воды с = 4,2 ∙ 103 Дж/(кг · К), удельная теплота парообразования воды r = 2,3 ∙ 106 Дж/кг.
Ответ: ∆U = m(c(t20 −t10 )+r) = 2,7 · 106 Дж.
Задача 30. Сосуд массой m = 2 кг изготовлен из стали. Сосуд содержит ν = 5 моль идеального одноатомного газа объемом V = 100 см3. Ему сообщают Q = 500 Дж теплоты,
261

Решебник по физике
не давая газу расширяться. Найти изменение давления газа ∆U. Удельная теплоемкость стали c = 460 Дж/(кг · К).
νRQ | 5 | |
Ответ: ∆p = | = 2 | 10 Па. |
V(1,5νR +cm) | ||
Задача31.Ввертикальномцилиндреподпоршнемнаходится газ объемом V1 = 200 см3 при температуре Т1 = 350 К. Массапоршняm=30кг,площадьегооснованияS=100см2. Газнагрелина∆T=100К,сообщивемуQ=50кДжтеплоты. Найти изменение внутренней энергии газа ∆U. Трением поршня о стенки сосуда пренебречь. Атмосферное давление нормальное.
mg | V | ∆T | = 43 Дж. |
Ответ: ∆U = Q − p + | T1 | ||
S | 1 |
Задача 32. ν = 2 моль идеального газа, взятого при температуре Т1 = 350 К, изобарно расширились, совершив при этом работу А = 10 кДж. Во сколько раз увеличился при
этот объем газа? | ||||
Ответ: | V2 | =1+ | A | = 2,7. |
V | νRT | |||
1 | 1 | |||
Задача 33. ν молей идеального газа нагреваются так, что его температура изменяется от Т1 до Т2 прямо пропорционально квадрату давления газа. Определить совершенную при этом работу А.
Ответ: A = 0,5νR(T2 −T1).
Задача 34. Некоторая масса газа, занимающего объем V1 = 0,01 м3, находится под давлением p1 = 0,1 МПа и при температуре Т1 = 300 К. Газ нагревается вначале при постоянном объеме до температуры Т2 = 320 К, а затем при постоянном давлении до температуры Т3 = 350 К. Найти работу, совершенную газом при переходе из состояния 1 в состояние 3.
Ответ: A = p1V1 T3 −T2 = 100 Дж.
T2
262

2m1R
2. Молекулярная физика и термодинамика
Задача 35. В горизонтально расположенном цилиндрическом сосуде находится идеальный газ массой m1, закрытый поршнем массой m2. Вследствие изобарного расширения газа при его нагревании поршень приобретает ско-
рость v, двигаясь из состояния покоя. Внутренняя энергия газа U прямо пропорциональна его абсолютной температуре Т: U = kТ, где k — коэффициент пропорциональности. Молярная масса газа M. Какое количество теплоты передано газу при этом? Теплоемкостями сосуда и поршня можно пренебречь.
Ответ: Q = m2υ2 (Mk+m1R) .
Задача 36. Какое количество теплоты получает идеальныйодноатомныйгаз,переходяизсостояния1всостояние3 (рис.91),есливсостоянии1егодавлениеp1 =0,2МПа,аобъ-
ем V1 = 20 л?
Ответ: Q = 11,5p1V1 = 4,6 ∙ 104 Дж.
Задача37.Если идеальный газ перевести из состояния 1 в состояние 3 сначала изобарно (участок 1—2, рис. 92), а затем изохорно (участок 2—3), то будет произведена некоторая работа, а если переход из состояния 1 в состояние 3 произвести непосредственно по прямой 1—3, то работа
263

Решебник по физике
увеличится в n раз. Найти давление газа p3 в состоянии 3, если в состоянии 1 p1 = 100 кПа, а n = 5.
Ответ: p3 = p1 (2n−1) = 900 кПа.
Задача 38. Температура нагревателя идеальной тепловой машины равна t1° = 117 °С, а холодильника t2° = 27 °С. Количество теплоты, получаемое машиной от нагревателя за t = 1 с, равно Q1 = 60 кДж. Найти количество теплоты Q2, отдаваемое холодильнику за это время, и мощность машины N.
= Q1 | T2 | 4 | Q −Q | 4 |
Ответ: Q2 | = 4,6 ∙ 10 Дж, N = | 1 2 | = 1,4 ∙ 10 Вт. | |
T1 | ||||
t | ||||
Задача 39. Паровая машина мощностью N = 14,7 кВт потребляет за t = 1 ч работы m = 8,1 кг угля с удельной теплотой сгорания (или теплотворной способностью, это одно и то же) q = 3,3 ∙ 107 Дж/кг. Температура котла t1° = = 200 °С, температура холодильника t2°= 58 °С. Найти фактический КПД ηф этой машины. Определить, во сколько раз КПД ηид идеальной тепловой машины, работающей по циклу Карно при тех же температурах нагревателя и холодильника, превосходит КПД этой паровой машины ηф.
Nt | ηид | T −T | ||
84 | = | 1 | 2 | |
Ответ: ηф = mq | 100% = 20 %, | 100%. = 1,5. | ||
ηф | T ηф | |||
D | 1 | D | ||
Задача40.Для ванны необходимо приготовить V = 320 л воды при температуре t = 40 °С. Из горячего крана смесителя идет вода при t1 = 70 °С, а из холодного — при 40 °С. Сколько горячей и холодной воды нужно влить, чтобы приготовить ванну?
Ответ: V1 = Vt(1t−−tt22 ) =145 л, V2 = V −V1 =175л.
Задача 41. В сосуд с водой массой m1 = 250 г при температуре t1° = 18 °С, опустили медную гирьку массой m1 = = 100 г, нагретую до t2° = 90 °С. После этого в сосуде установилась температура t° = 20 °С. Удельная теплоемкость
264

t−t1
2. Молекулярная физика и термодинамика
воды с1 = 4186 Дж/(кг ∙ К), удельная теплоемкость меди с2 = 380 Дж/(кг ∙ К). Определить теплоемкость сосуда С.
Ответ: C = c2m2 (t2 −t) −c1m1 (t−t1) = 284 Дж/К.
Задача 42. В сосуд, содержащий m1 = 8 кг воды при Т1 = = 280 К,положиликусокльдаприТ2=280 К,послечеготемператураобразовавшегосяльдасталаТ3=270 К.Какаямасса льдаm2 былаположенавводу?Теплоемкостьюсосудапренебречь. Удельная теплоемкость воды с1 = 4186 Дж/(кг ∙ К), удельнаятеплотаплавленияльдаλ= 2,1∙103 Дж/кг,удельная теплоемкость льда с2 = 2,1 ∙ 103 Дж/(кг ∙ К). Температура плавления льда и кристаллизации воды Т0 = 273 К.
Ответ: m2 = m1 c1 (T1 −T0 )(+λ−+c2)(T0 −T3 ) = 3,5 кг. c2 T3 T2
Задача 43. В сосуд с теплоемкостью C налита вода массой m1, в которой плавает лед массой m2. В сосуд впускают пар массой m3 при температуре t1° выше 100 °C. Какая температура t° установится в сосуде при тепловом равновесии, если известно, что весь лед растаял, а пар сконденсировался? Удельная теплоемкость воды с1, удельная теплоемкость пара с2, удельная теплота плавления льда λ, удельная теплота парообразования воды r.
t0 < t < t2,
где t0 = 0 °С и t2 = 27 °С t2 = 100 °С.
Ответ: t0 = m3 ((c2 (t1 −t(2 )+ L+c1t2 )−)m) 2λ. C” +c1 m1 +m2 +m3
Задача44.В стеклянной пробирке массой m1 находится лед массой m2, взятый при отрицательной температуре t1°. Поместив пробирку над горящей спиртовкой, этот лед переводят в стоградусный пар (t2° = 100 °С). Какую массу спирта m3 пришлось при этом сжечь? Удельная теплоемкость стекла с1, удельная теплоемкость льда с2, удельная
265

Решебник по физике
теплота плавления льда λ, удельная теплоемкость воды с3, удельная теплота парообразования воды r, температура таяния льда t0° = 0 °С. КПД спиртовки равен η. Удельная теплота сгорания спирта q
Ответ:
m3 = 100ηq%(c1m1 (t2 −t1)+m2 (c2 (t0 −t1)+λ+c3 (t2 −t0 )+r)).
Задача45.Алюминиевыйчайникмассойm1=1кгсодержит m2 = 2 кг воды при t1 = 20 °C. Чайник с водой ставят на примус, в котором сгорает m3 = 50 г керосина. Какая масса водыm4приэтомвыкипит,еслитепловыепотерисоставляют 60%?Удельнаятеплоемкостьалюминияс1 =880Дж/(кг∙К), удельная теплоемкость воды с2 = 4186 Дж/(кг ∙ К), удельная теплота сгорания керосина q = 4,6 ∙ 107 Дж/кг, удельная теплота парообразования воды r = 2,3 ∙ 106 Дж/кг, температура кипения воды t2 = 100 °С.
Ответ: m = | 1 | m3qη | −(t −t )(c m +c m ) | = 0,08 кг. | |
4 | r | 2 1 1 1 2 2 | |||
100% | |||||
Задача 46. Два свинцовых шарика одинаковой массы движутся горизонтально со скоростями v и 2v навстречу друг другу. Определить повышение температуры ∆Т этих шаров в результате их неупругого соударения.
Ответ: ∆T = 1,125v2 . c
Задача 47. С высоты Н свободно падает кусок металла с удельной теплоемкостью c. На сколько градусов поднялась его температура, если 10 % его первоначальной механической энергии при ударе о землю превратилось в теплоту?
Ответ: ∆T = c η100%gH .
Задача 48. Свинцовая пуля пробивает стену. Скорость пули до удара v0 = 350 м/с, после удара v = 200 м/с. Температура пули перед ударом t1 = 30 °С. Найти, какая часть
266

2. Молекулярная физика и термодинамика
пули расплавилась. Температура плавления свинца t2 = = 327 °С, удельная теплоемкость свинцас = 130 Дж/(кг∙ К), удельная теплота плавления свинца λ = 25 кДж/(кг ∙ К).
Ответ: | ∆m | = | v12 −v22 −2c(t2 | −t1) | = 0,1. |
m1 | 2λ −v22 | ||||
Задача 49. С какой скоростью v должны лететь навстречу друг другу две одинаковые льдинки, имеющие температуру t1 = –10 °С, чтобы при соударении они обратились в пар при t2 = 100 °С? Удельная теплоемкость льда c1 = 2,1 ∙ 103 Дж/(кг ∙ К), удельная теплота плавления льда λ = 3,3 ∙ 10 Дж/кг, удельная теплоемкость воды c2 = = 4,2 ∙ 103 Дж/(кг ∙ К), температура таяния льда t0° = 0 °С, удельная теплота парообразования воды r = 2,3 ∙ 106 Дж/кг.
Ответ: υ = 2(c1 (t0 −t1)+λ+c2 (t2 −t0 )+r) = 2,5 км/с
Задача 50. Какую массу m1 керосина потребовалось бы сжечь, чтобы вывести спутник массой m2 = 1 т на круговую орбиту вблизи поверхности Земли, если бы все количество теплоты, выделенной керосином, превратилось в механическую энергию спутника? Радиус Земли R = 6,4 ∙ 106 м, удельная теплота сгорания керосина q = 46 МДж/кг.
Ответ: m1 = m22gRq = 682 кг.
Задача51.Автомобиль массой m1 = 4,6 т трогается с места и на подъеме tg α = 0,025, двигаясь равноускоренно, заt=40спроходитS=200м.НайтиобъемVсгоревшегопри этом бензина, если коэффициент сопротивления движению μ=0,02иКПДподъемаη=20%.Удельнаятеплотасгорания бензина q = 46 МДж/кг, плотность бензина ρ = 800 кг/м3.
m S 2S | |||||
Ответ: V = | 1 | + g(tgα+μ) | 100% | = 8,6 ∙ 10–5 м3. | |
ρqη t2 | |||||
Задача52.Стальной осколок, падая с высоты h = 500 м, имел у поверхности земли скорость v = 50 м/с. Насколько
267

Ответ: ∆T =
Решебник по физике
повысилась температура осколка, если считать, что вся работа сопротивления воздуха пошла на его нагревание? Начальная скорость осколка равна нулю. Удельная теплоемкость стали c = 460 Дж/(кг ∙ К).
1 | v2 | ||
Ответ: ∆T = | gh− | = 8 К. | |
c | 2 | ||
Задача 53. Маленький шарик из вещества с удельной теплоемкостью c, подвешенный на нити длиной l, отклонили на угол α1 от положения равновесия и отпустили. После неупругого удара о вертикальную стенку он отклонился на меньший угол α2. Найти повышение температуры шарика ∆Т. Теплоемкостью стенки пренебречь.
Ответ: ∆T = glc (cosα2 −cosα1).
Задача 54. Тело соскальзывает без начальной скорости с наклонной плоскости длиной l , которая образует с горизонтом угол α. Скорость тела у основания наклонной плос-
кости v. Найти повышение температуры тела ∆Т вследствие трения о наклонную плоскость. Удельная теплоемкость его вещества c. На нагревание тела пошло четверть всей выделившейся при трении теплоты.
2glsinα −v2 .
8c
268
Раздел 3. Электромагнетизм
Краткая теория и советы к решению задач
Электромагнетизм включает электростатику, законы постоянного тока и магнетизм.
1)Электростатика
Взадачах электростатики рассматривают взаимодейс твие зарядов и действие электрических полей неподвиж ных зарядов на заряды, внесенные в эти поля.
Количественноймеройвзаимодействиязаряженныхтел является электрический заряд q. Заряд может быть поло жительным и отрицательным.
Наименьшим (элементарным) положительным зарядом обладает элементарная частица «протон», входящая в со став ядра атома. Наименьшим (элементарным) отрицатель ным зарядом обладает элементарная частица «электрон», входящая в состав атома.
Элементарный положительный заряд по модулю равен элементарному отрицательному заряду и отличается от него лишь знаком.
Заряд электрона е равен по модулю заряду протона.
е= 1,6 ∙ 10–19 Кл.
Заряды одного знака (одноименные заряды) отталкива ются друг от друга, а заряды противоположных знаков (разноименные заряды) притягиваются друг к другу.
Электрическиезарядырождаютсятолькопарами.Вкаж дой такой паре заряды равны по модулю и противополож ны по знаку. Если два равных по модулю и противополож ных по знаку заряда привести в соприкосновение, то они
269
Источник
Задачи на количество теплоты с решениями
Формулы, используемые на уроках «Задачи на количество теплоты,
удельную теплоемкость».
1 г = 0,001 кг; 1 т = 1000 кг; 1 кДж = 1000 Дж; 1 МДж = 1000000 Дж
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?
При решении задачи нужно учесть, что оба тела — и котёл, и вода — будут нагреваться вместе. Между ними происходит теплообмен. Их температуры можно считать одинаковыми, т. е. температура котла и воды изменяется на 100 °С — 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми. Ведь их массы и удельные теплоёмкости различны.

Задача № 2.
Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.

Задача № 3.
Стальная деталь массой 3 кг нагрелась от 25 до 45 °С. Какое количество теплоты было израсходовано?

Задача № 4.
В сосуде содержится 3 л воды при температуре 20 °С. Сколько воды при температуре 45 °С надо добавить в сосуд, чтобы в нём установилась температура 30 °С? Необходимый свободный объём в сосуде имеется. Теплообменом с окружающей средой пренебречь

Задача № 5.
На сколько градусов изменилась температура чугунной детали массой 12 кг, если при остывании она отдала 648000 Дж теплоты?

Задача № 6.
По графику определите удельную теплоёмкость образца, если его масса 50 г.
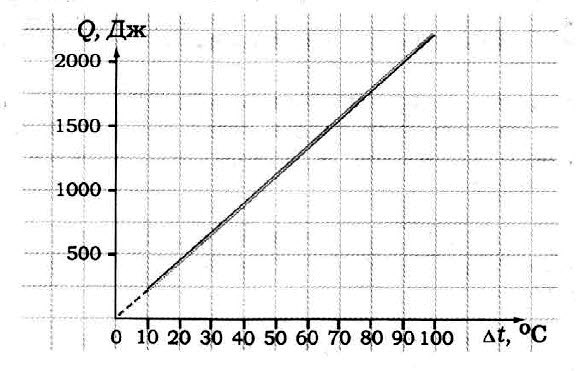

Задача № 7.
Для нагревания медного бруска массой 3 кг от 20 до 30 °С потребовалось 12000 Дж теплоты. Какова удельная теплоемкость меди?

Задача № 8.
Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей 2,1 кДж энергии. Чему равна удельная теплоемкость камня?
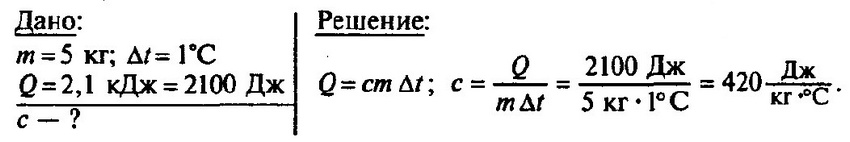
Задача № 9.
Какое количество теплоты потребуется для нагревания на 1 °С воды объемом 0,5 л; олова массой 500 г; серебра объемом 2 см3; стали объемом 0,5 м3; латуни массой 0,2 т?

Задача № 10.
Какое количество теплоты получили алюминиевая кастрюля массой 200 г и находящаяся в ней вода объемом 1,5 л при нагревании от 20 °С до кипения при температуре 100 °С?

Задача № 11.
а) Воздух, заполняющий объем 0,5 л в цилиндре с легким поршнем, нагрели от 0 до 30 °С при постоянном атмосферном давлении. Какое количество теплоты получил воздух?
б) В порожнем закрытом металлическом баке вместимостью 60 м3 под действием солнечного излучения воздух нагрелся от 0 до 20 °С. Как и на сколько изменилась внутренняя энергия воздуха в баке? (Удельная теплоемкость воздуха при постоянном объеме равна 720 Дж/кг-°С.)

Задача № 12.
ОГЭ
Металлический цилиндр массой m = 60 г нагрели в кипятке до температуры t = 100 °С и опустили в воду, масса которой mв = 300 г, а температура tв = 24 °С. Температура воды и цилиндра стала равной Θ = 27 °С. Найти удельную теплоёмкость металла, из которого изготовлен цилиндр. Удельная теплоёмкость воды св = 4200 Дж/(кг К).

Задача № 13.
В теплоизолированном сосуде сначала смешивают три порции воды 100 г, 200 г и 300 г с начальными температурами 20 °C, 70 °C и 50 °C соответственно. После установления теплового равновесия в сосуд добавляют новую порцию воды массой 400 г при температуре 20 °C. Определите конечную температуру в сосуде. Ответ дайте в °C, округлив до целого числа. Теплоёмкостью калориметра пренебрегите.
Решение.

Ответ: 39 °С.
Задача № 14. (повышенной сложности)
Стальной шарик радиусом 5 см, нагретый до температуры 500 ˚С, положили на лед, температура которого 0 ˚С. На какую глубину погрузится шарик в лед? (Считать, что шарик погрузился в лед полностью. Теплопроводностью шарика и нагреванием воды пренебречь.)
Дано: R = 0,05 м; t1 = 500 ˚С; t2 = 0 ˚С;
ρ1 (плотность стали) = 7800 кг/м3.;
ρ2 (плотность льда) = 900 кг/м3.
c (удельная теплоемкость стали) = 460 Дж/кг •˚С,
λ (удельная теплота плавления льда) = 3,3 • 105 Дж/кг,
Найти: h – ?

Краткая теория для решения Задачи на количество теплоты.

Конспект урока «Задачи на количество теплоты».
Посмотреть конспект урока по теме «Количество теплоты. Удельная теплоемкость»
Следующая тема: «ЗАДАЧИ на сгорание топлива с решениями».
Источник
