В сосуд с водой опустили стеклянную трубку нижний конец которой
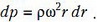
Можаев В. Задачи с жидкостями //Квант. — 2006. — № 1. — С. 40-43.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
В этой статье будут рассмотрены задачи, в которых жидкость, с одной стороны, является средой, где находятся твердые тела, а с другой стороны, она, как жидкий элемент, участвует в движении, подобно твердому телу. Наиболее сложными являются комбинированные задачи, в которых жидкость движется вместе с находящимся в ней твердым телом (например, разобранная ниже задача 6).
Перейдем к обсуждению конкретных задач.
Задача 1. В цилиндрический сосуд с водой опустили кусок льда, в который вморожен осколок стекла. При этом уровень воды в сосуде поднялся на h = 11 мм, а лед остался на плаву, целиком погрузившись в воду. На сколько опустится уровень воды в сосуде после того, как весь лед растает? Плотность воды ρв = 1 г/см3, плотность льда ρл = 0,9 г/см3, стекла ρст = 2,0 г/см3
Обозначим первоначальный объем льда через Vл, а объем стекла — через Vст. Когда кусок льда полностью погрузился в воду, он вытеснил объем воды, равный
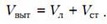
Очевидно, что этот же объем равен
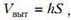
где S — площадь поперечного сечения сосуда.
Теперь запишем условие плавания куска льда с вмороженным осколком стекла — суммарная сила тяжести льда и стекла равна выталкивающей силе:
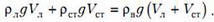
Из совместного решения полученных уравнений найдем объемы льда и стекла:
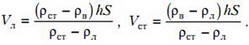
Из растаявшего льда образовалась вода объемом
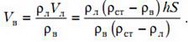
Поскольку кусок стекла остается в воде, понижение уровня воды в сосуде за время таяния льда будет равно
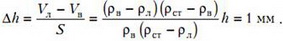
Задача 2. В вертикально расположенной трубке — с открытым верхним концом, с постоянным внутренним сечением и длиной 3L = 1080 мм — столбиком ртути длиной L заперт слой воздуха такой же длины. Какой длины столб ртути останется в трубке, если ее перевернуть открытым концом вниз? Внешнее давление p0 = 774 мм рт. ст.
Обозначим давление воздуха под ртутным столбиком в исходном положении трубки через p1. Тогда условие равновесия столбика ртути длиной L запишется в виде
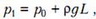
где ρ – плотность ртути. Предположим, что после переворота трубки и установления первоначальной температуры часть ртути выльется. Обозначим через h длину столбика оставшейся в трубке ртути. Новое условие равновесия будет иметь вид
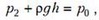
где p2 – новое давление воздуха над ртутным столбиком.
Условие сохранения количества изолированного воздуха позволяет записать
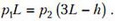
Подставляя сюда p1 из первого равенства, а p2 – из второго, получим уравнение относительно h:
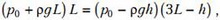
или, если записать атмосферное давление в виде , где H0 = 774 мм:
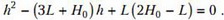
Для данных численных значений L и H0 (в мм) получается, что
h = 270 мм.
Задача 3. U–образная трубка расположена вертикально и заполнена жидкостью. Один конец трубки открыт в атмосферу, а другой конец соединен с сосудом объемом V0 = 0,1 л, заполненным гелием (рис. 1). Объем всей трубки равен объему этого сосуда. В некоторый момент гелий начинают медленно нагревать. Какое минимальное количество теплоты необходимо подвести к гелию, чтобы вся жидкость вылилась из трубки? Атмосферное давление p0 = 105 Па; длины трех колен трубки одинаковы; давление, создаваемое столбом жидкости в вертикальном колене, равно p0/8.
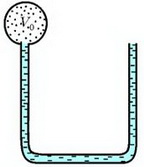
Рис. 1
Обозначим полную длину трубки через 3L, а площадь внутреннего поперечного сечения трубки – S. Поскольку объем трубки V0, то длина каждого колена
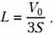
Весь процесс нагрева гелия можно разбить на три участка. Первый участок — это когда жидкость еще находится в левом вертикальном колене. Рассмотрим момент времени, когда уровень жидкости в левом колене переместился на величину z, . Из условия равновесия жидкости в трубке найдем давление гелия:
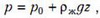
где ρж – плотность жидкости. На втором участке, для которого , давление гелия
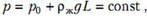
а на третьем участке, для
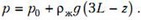
На рисунке 2 изображен график зависимости давления гелия от его объема V, который связан со смещением z простым соотношением:
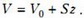
На первых двух участках тепло необходимо подводить к гелию — это однозначно: здесь газ, расширяясь, совершает работу и одновременно нагревается. А вот третий участок неоднозначен: здесь газ также совершает работу, но при этом он может и охлаждаться. Убедимся, что и на этом участке тепло тоже подводится.
Учитывая, что , запишем уравнение процесса для третьего участка в виде
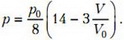
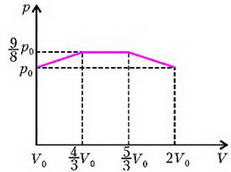
Рис. 2.
Рассмотрим малое изменение объема ΔV. Тогда работа, совершенная гелием, равна
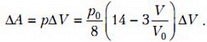
Запишем уравнение состояния гелия как идеального газа:
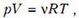
где ν – количество вещества, Т – температура газа. Подставим в это уравнение выражение для давления на третьем участке процесса и получим
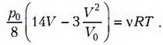
Продифференцируем обе части этого уравнения:
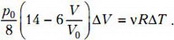
Теперь найдем изменение внутренней энергии гелия при изменении объема на ΔV:
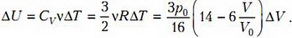
Согласно первому началу термодинамики, подведенное количество теплоты равно сумме изменения внутренней энергии газа и совершенной им работы:
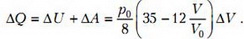
Легко убедиться, что при и
Итак, на всех участках тепло подводится, поэтому полное подведенное к гелию количество теплоты Q найдем как сумму полного изменения внутренней энергии и полной работы, которую совершил гелий:
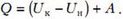
Поскольку начальная и конечная температуры равны, соответственно,
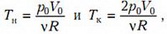
то изменение внутренней энергии равно
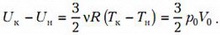
Полную работу найдем как площадь под кривой на рисунке 2:
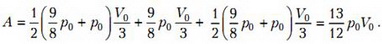
Тогда окончательно
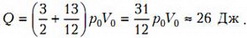
Задача 4. «Тройник» с двумя открытыми в атмосферу вертикальными трубками и одной закрытой (горизонтальная трубка) полностью заполнен водой (рис. 3). После того, как тройник начали двигать по горизонтали в плоскости рисунка влево с некоторым постоянным ускорением, из него вылилась 1/16 массы всей воды. Чему при этом стало равно давление в жидкости у закрытого конца – в точке А? Трубки имеют одинаковые внутренние сечения. Длину L считать заданной. Диаметр трубок мал по сравнению с длиной L.
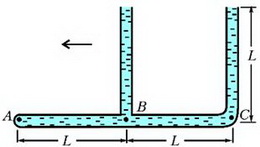
Рис. 3.
При движении тройника влево с ускорением а гидростатические давления в точках А, В и С (см. рис. 3) связаны между собой уравнением движения воды в горизонтальной трубке:
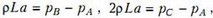
где ρ – плотность воды. Давление в точке С больше давления в точке В, поэтому вода будет выливаться из правой вертикальной трубки. Из условия неразрывности струи жидкость при этом будет отсасываться из левой вертикальной трубки. В установившемся режиме правая трубка будет полностью заполнена водой, а левая – частично. Поскольку вылилась 1/16 массы всей воды, что соответствует массе воды в части трубки длиной L/4, то в левой трубке останется столбик воды высотой 3/4L. Поэтому давления в точках В и С будут равны
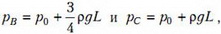
где p0 – атмосферное давление.
Исключая из всех уравнений рB и рС, получим систему двух уравнений относительно рА и а:
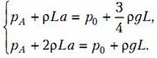
Решая эту систему относительно рА, найдем
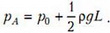
Задача 5. Тонкая, запаянная с одного конца и изогнутая под прямым углом трубка заполнена ртутью и закреплена на горизонтальной платформе, которая вращается с угловой скоростью ω вокруг вертикальной оси (рис. 4). При вращении платформы ртуть не выливается и полностью заполняет горизонтальное колено. Открытое колено трубки вертикально. Геометрические размеры установки указаны на рисунке; атмосферное давление р0; плотность ртути ρ. Найдите давление ртути у запаянного конца трубки.
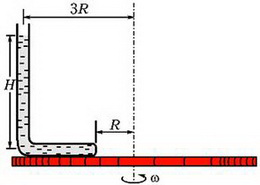
Рис. 4.
Выделим в горизонтальной части трубки небольшой элемент ртути длиной dr, расположенный на произвольном расстоянии r от оси вращения (рис. 5).
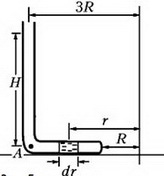
Рис. 5.
Этот элемент вращается в горизонтальной плоскости с угловой скоростью ω. Запишем уравнение движения выделенного элемента:
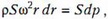
где S – площадь поперечного сечения трубки, dp – разность давлений между левым концом элемента ртути и правым. После сокращения на S получим связь между малыми приращениями dp и dr:
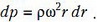
Проинтегрируем обе части этого уравнения и получим
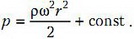
Константу определим из условия, что при r = 3R (точка А) давление равно
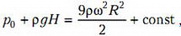
и получим зависимость p(r)
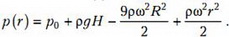
Отсюда найдем давление ртути у запаянного конца трубки (r = R):
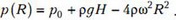
Задача 6. Стеклянный шар объемом V и плотностью ρ находится в сосуде с водой (рис. 6). Угол между стенкой сосуда и горизонтальным дном α, внутренняя поверхность сосуда гладкая, плотность воды ρ0. Найдите силу давления шара на дно сосуда в двух случаях: 1) сосуд неподвижен; 2) сосуд движется с постоянным горизонтальным ускорением а.
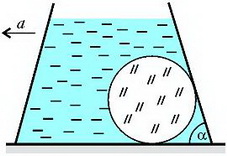
Рис. 6.
Сначала рассмотрим движущийся по горизонтали с постоянным ускорением а сосуд с водой. Введем систему координат XY, связанную с сосудом, как это изображено на рисунке 7.
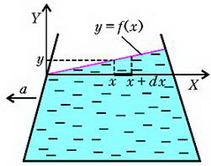
Рис. 7.
Наша задача – найти уравнение свободной поверхности жидкости в сосуде, который движется с горизонтальным ускорением а. Для этого выделим маленький элемент жидкости на оси Х, длина которого dx, а площадь поперечного сечения равна единице. С левого торца этого элемента давление равно
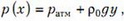
а с правого торца оно равно
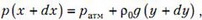
где у – высота столба жидкости в точке х, а – аналогичная высота в точке . Так как наш элемент жидкости движется с ускорением а, его уравнение движения имеет вид
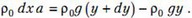
Отсюда получаем
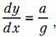
или в интегральном виде —
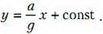
Поскольку при х = 0 у = 0, константа тоже равна нулю, а уравнение свободной поверхности жидкости выглядит так:
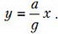
Линии, параллельные свободной поверхности, внутри жидкости являются линиями постоянного давления. Таким образом, жидкость, движущаяся с горизонтальным ускорением а, эквивалентна неподвижной жидкости, находящейся в новом поле тяжести с эффективным «ускорением свободного падения», равным и направленным под углом к вертикали (рис. 8). Вертикальная составляющая этого эффективного ускорения равна обычному ускорению свободного падения g, а горизонтальная составляющая численно равна ускорению сосуда и направлена в противоположную сторону.
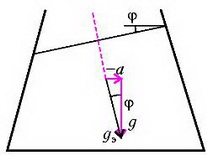
Рис. 8.
В том случае, когда сосуд неподвижен (а = 0), эффективное ускорение равно g и направлено по вертикали. Силы, действующие на стеклянный шар в этом случае, показаны на рисунке 9.
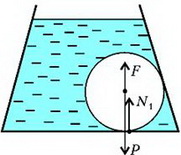
Рис. 9.
Здесь – вес (точнее – сила тяжести) шара, – выталкивающая сила, а N1 – сила реакции дна сосуда на шар. Из условия равновесия шара найдем, что
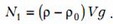
Очевидно, что сила давления шара на дно численно равна силе реакции дна и направлена в противоположную сторону.
В случае движущейся с горизонтальным ускорением a жидкости или неподвижной жидкости, но находящейся в поле с новым «ускорением свободного падения» gЭ, на шар будут действовать следующие силы (рис.10): вертикальная составляющая нового веса шара , горизонтальная составляющая этого веса , вертикальная составляющая выталкивающей силы , ее горизонтальная составляющая , реакция опоры Т со стороны боковой стенки и, наконец, сила N2 – сила реакции на шар со стороны дна сосуда. Запишем условие равновесия шара, т.е. равенство нулю всех сил, действующих на шар по вертикали:
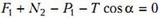
и по горизонтали:
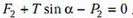
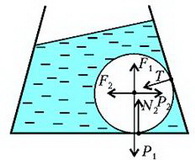
Рис. 10.
Исключая из этих уравнений Т, найдем искомую силу N2:
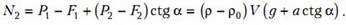
Разумеется, и в этом случае сила давления шара на дно сосуда численно равна силе реакции дна, но направлена в противоположную сторону.
Упражнения.
1. В цилиндрическом сосуде с водой плавает деревянная дощечка. Если на нее сверху положить стеклянную пластинку, то дощечка с пластинкой останутся на плаву, а уровень воды в сосуде повысится на Δh1. На сколько изменится уровень воды в сосуде с плавающей дощечкой, если ту же стеклянную пластинку бросить на дно сосуда? Плотность стекла ρст, плотность воды ρв.
2. U–образная трубка состоит из трех одинаковых колен, расположена вертикально и заполнена жидкостью (см. рис. 1). Один конец трубки соединен с баллоном, заполненным водородом, другой конец открыт в атмосферу. Водород в баллоне медленно нагревают, и он постепенно вытесняет жидкость из трубки. К моменту, когда из трубки вылилось 2/3 всей массы жидкости, водород получил количество теплоты Q = 30 Дж. Найдите объем баллона. Известно, что объем всей трубки равен объему баллона; атмосферное давление p0 = 105 Па; давление, создаваемое столбом жидкости в вертикальном колене трубки, равно p0/9.
3. «Тройник» из трех вертикальных открытых в атмосферу трубок полностью заполнен водой (рис. 11). После того, как тройник начали двигать в горизонтальном направлении в плоскости рисунка с некоторым ускорением, из него вылилось 9/32 всей массы воды. Чему равно ускорение тройника? Внутренние сечения трубок одинаковы, длина каждой трубки L.
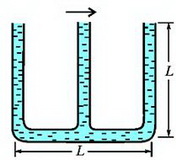
Рис. 11
4. Тонкая, запаянная с одного конца и изогнутая под прямым углом трубка заполнена жидкостью и закреплена на горизонтальной платформе, вращающейся с угловой скоростью ω вокруг вертикальной оси (рис. 12). Открытое колено трубки вертикально. Геометрические размеры установки указаны на рисунке; атмосферное давление p0; плотность жидкости ρ. Найдите давление жидкости у запаянного конца трубки.
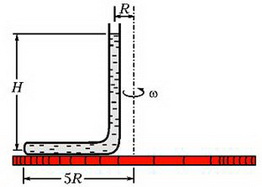
Рис. 12
Ответы.
1.
2.
3. .
4.
Источник
В.Ф.ШИЛОВ,
ИСМО РАО, г. Москва
Далеко не очевидный факт для учащихся
– воздух имеет вес – когда-то доказывался
опытным путём, а именно взвешиванием стеклянного
шара ёмкостью 1 л. Такие шары уже не выпускают,
но можно воспользоваться колбой ёмкостью 1 л.
Колбу закрывают каучуковой пробкой с плотно
посаженной по центру стеклянной трубкой, которая
снабжена притёртым краном. С такой колбой можно
поставить и ещё ряд опытов.
1. Необходимость среды для
распространения звука. Звук хорошо
распространяется в твёрдой, жидкой и
газообразной средах, но не распространяется в
вакууме. Для доказательства этого утверждения в
колбу помещают малогабаритный, например, от
плеера, телефонный наушник. Для этого в пробке
шилом протыкают два отверстия и через них
пассатижами проталкивают медную проволоку
диаметром до 1 мм. К нижним концам проводников
присоединяют телефон (наушник), а к верхним –
провода от выходных зажимов звукового
генератора.
Стеклянную трубку соединяют с
разрежающим тубусом насоса. Открывают кран и
наблюдают, как по мере откачивания воздуха из
колбы звучание телефона становится всё слабее и
слабее. Полностью звучание не прекращается из-за
неполного откачивания воздуха и
звукопроводности проводов.
2. Демонстрация устойчивого
равновесия. В колбу насыпают песок на треть,
наливают немного воды для смачивания песка и
закрепляют колбу вертикально в штативе. Когда
вода отстоится, её излишки сливают, чтобы
закрепить песок в нижней части колбы.
Затем колбу ставят на поверхность
стола. При отклонении горла колбы в сторону, она
возвращается в первоначальное положение, т.е.
ведёт себя как «ванька-встанька», демонстрируя
устойчивое равновесие.
3. Конвекционные потоки в жидкости.
В колбу наливают воду примерно до половины и
закрепляют в штативе. В воду опускают стеклянную
трубочку так, чтобы она одним концом касалась
дна, и через неё насыпают кристаллики
марганцовки. Закрыв пальцем верхний конец
трубочки, вынимают её. Под колбу помещают слабо
горящую спиртовку и наблюдают, как бор-довые
струйки поднимаются в середине колбы и опадают
вдоль стенок, – это конвекционные потоки,
благодаря которым вода постепенно окрашивается
однородно в бордовый цвет.
4. Объёмное расширения воздуха и
воды. Коэффициент объёмного расширения
определяют с помощью экспериментальной
установки, изображённой на рисунке. В колбу
наливают воду (лучше подкрашенную) и
рассчитывают коэффициент по формуле , где ![]() V (приращение объёма) определяют по
V (приращение объёма) определяют по
показаниям шприца, ![]() t
t
(изменение температуры) – по термометру
мультиметра, V0 (начальный объём колбы)
определяют по показаниям измерительного
цилиндра, выливая в него воду.
5. Изменение плотности воды при
замерзании. Колбу заполняют водой (лучше её
подкрасить) и закрывают пробкой, через которую
пропущены провода термопары, подсоединённые к
термометру мультиметра, и стеклянная трубочка.
Колбу закрепляют в штативе и опускают в сосуд из
прозрачной пластиковой бутылки. Сосуд заполняют
охлаждающей смесью изо льда и соли. Через равные
промежутки времени записывают температуру и
уровень воды в трубочке. Смесь в сосуде
периодически встряхивают.
По мере охлаждения колбы объём воды в
трубочке уменьшается до тех пор, пока
температура не станет равной 4 °С, после чего
объём воды начинает увеличиваться, хотя
температура всё понижается до 0 °С. Это говорит
о том, что вода имеет минимальный объём и
наибольшую плотность при 4 °С.
6. Кристаллизация гипосульфита.
Заполнив колбу гипосульфитом, расплавляют его на
слабом огне. Затем гипосульфит охлаждают до
комнатной температуры, но он остаётся жидким,
хотя температура отвердевания его выше
комнатной. Через трубочку опускают несколько
мелких кристалликов твёрдого гипосульфита,
которые, попадая в жидкую фазу, моментально
вызывают кристаллизацию вещества по всему
объёму. Коснувшись колбы спаем термопары,
фиксируют повышение температуры. Это
свидетельствует о том, что внутренняя энергия
вещества в жидкой фазе больше внутренней энергии
этого же вещества в твёрдом состоянии.
7. Модель пульверизатора. С
помощью груши воздух продувают через
горизонтальную стеклянную трубочку. При этом над
отверстием вертикальной трубочки, опущенной в
колбу с водой, согласно закону Бернулли,
возникает разрежение, и атмосферное давление
гонит воду вверх по трубочке. Вода
подхватывается струёй воздуха и распыляется.
Чтобы атмосферное давление «работало», в пробке
должно быть сквозное отверстие.
8. Необходимость атмосферного
давления для работы насоса. Если колбу
полностью наполнить водой и в отверстие в пробке
вставить хвостовик шприца так, чтобы в месте
соединения пробки и шприца не было воздуха, то
поднять поршень шприца не удастся, потому что на
воду не будет действовать атмосферное давление.
9. Получение направленной струи
воды. Собирают установку по рисунку,
закрывают зажим. Нагнетают воздух в колбу и
закрывают кран – вода в колбе будет находиться
под давлением больше атмосферного. Если зажим
открыть, вода начнёт бить узкой струёй, которую
можно направить на водяное колесо или водяную
турбину.
С помощью этой струи можно также
демонстрировать траекторию движения тела,
брошенного горизонтально или под углом к
горизонту.
Для надёжности пробку следует
закрепить на колбе изоляционной лентой или
скотчем, а лучше – проволокой, как это делают с
бутылкой шампанского.
10. Нагревание проводов линии
электропередачи. В колбу помещают несколько
метров тонкого двухжильного провода, а
стеклянную трубку, ведущую в колбу, соединяют с
жидкостным манометром. Вначале подсоединяют
провод к источнику низкого напряжения (4 В).
Увеличивая ток с помощью реостата, который
является в данном случае потребителем, наблюдают
увеличение показаний манометра в результате
расширения воздуха в колбе при нагревании
проводов. Затем подсоединяют провода к источнику
более высокого напряжения (36 В), и убеждаются в
том, что при передаче той же мощности провода
практически не греются.
11. Моделирование хода лучей
света в глазу. Колба с водой – это
сферическая линза и может служить моделью глаза.
Колбу наполняют мыльной водой, чтобы был виден
ход лучей света. От осветителя на неё направляют
пучок параллельных лучей через собирающую линзу
так, чтобы лучи фокусировались на задней стенке
колбы. Линза моделирует хрусталик глаза, задняя
стенка колбы – сетчатку. Для нормального глаза
изображение получается на сетчатке.
Статья подготовлена при поддержке компании «Техпроммаркет». Надежное оборудование-это залог долговечной работы изделий и приборов. Для того чтобы приобрести качественное оборудование требуется затратить малое усилие: зайти на сайт www.TehpromMarket.Ru. На сайте вы сможете приобрести стальной фланцевый кран, клапаны, электроприводы и вентили. В компании «Техпроммаркет» клиент – это не просто покупатель, а прежде всего человек.
Заменяют «нормальную» линзу на линзу с
более коротким фокусным расстоянием и получают
изображение перед сетчаткой – модель
близорукого глаза. Для коррекции «зрения»
впереди ставят рассеивающую линзу и получают
изображение на сетчатке.
Источник
