В сосуд с жидкостью погружают маленький датчик манометра
5. Механика (объяснение явлений)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
На рисунке представлены графики зависимости давления (p) от глубины погружения (h) для двух покоящихся жидкостей: воды и тяжёлой жидкости дийодметана, при постоянной температуре.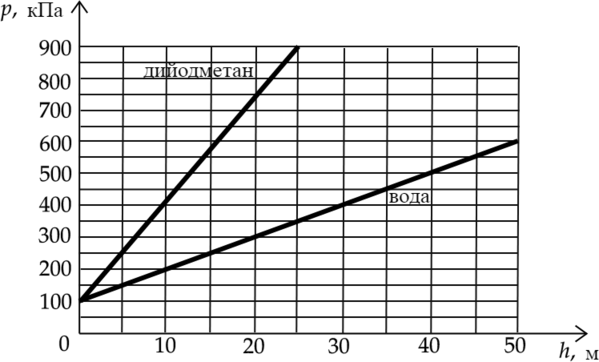 
Выберите два верных утверждения, согласующихся с приведёнными графиками.
1) Если внутри пустотелого шарика давление равно атмосферному, то в воде на глубине 10 м давления на его поверхность извне и изнутри будут равны друг другу.
2) Плотность керосина 0,82 г/см(^3), аналогичный график зависимости давления от глубины для керосина окажется между графиками для воды и дийодметана.
3) В воде на глубине 25 м давление p в 2,5 раза больше атмосферного.
4) С ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде.
5) Плотность оливкового масла 0,92 г/см(^3), аналогичный график зависимости давления от глубины для масла окажется между графиком для воды и осью абсцисс (горизонтальной осью).
Полное давление (p) складывается из атмосферного давления (p_a) и гидростатического давления столба жидкости: [p=rho gh+p_a] 1) Как видно из графика, давление воды на глубине 10 м принимает значение 200 кПа, что в два раза больше атмосферного давления (Атмосферное давление 100 кПа).
Утверждение 1 – (color{red}{small text{Неверно}})
2) Так как плотность керосина меньше чем плотность воды, то его аналогичный график окажется между графиком для воды и осью абсцисс.
Утверждение 2 – (color{red}{small text{Неверно}})
3) Давление в воде на глубине 25 м равно 350 кПа, что в 3,5 раза больше атмосферного.
Утверждение 3 – (color{red}{small text{Неверно}})
4) Так как прямая давления в дийодметане лежит выше прямой давления в воде, то это означает, что давление в дийодметане возрастает быстрее, чем в воде.
Утверждение 4 – (color{green}{small text{Верно}})
5) Так как плотность оливкого масла меньше чем плотность воды, то его аналогичный график окажется между графиком для воды и осью абсцисс.
Утверждение 5 – (color{green}{small text{Верно}})
Ответ: 45
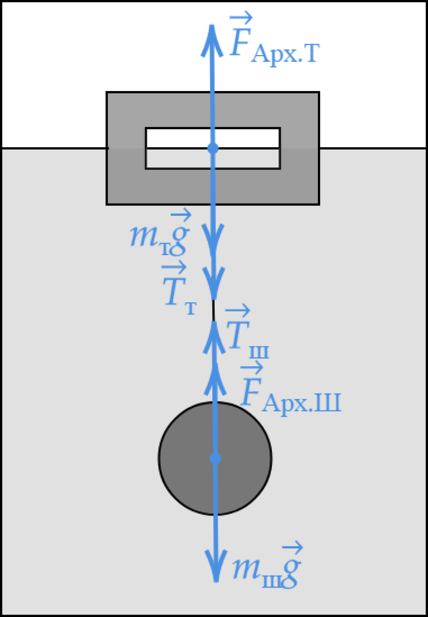
К телу, имеющему внутреннюю герметичную полость, на невесомой нерастяжимой нити привязан сплошной шарик. Система «тело + шарик» плавает в сосуде с жидкостью, не касаясь стенок и дна сосуда. Плотность материала тела и шарика 1,6 г/см(^3), плотность жидкости 800 кг/м(^3), объём полости составляет 3/4 объёма тела, объём шарика равен 1/4 объёма тела. Исходя из условия задачи, выберите два верных утверждения.
1) Модуль силы Архимеда, действующей на тело, меньше модуля силы Архимеда, действующей на шарик.
2) Модуль силы натяжения нити равен модулю силы тяжести, действующей на шарик.
3) Модуль силы натяжения нити меньше модуля силы Архимеда, действующей на тело.
4) Модуль силы тяжести, действующей на шарик, равен модулю силы тяжести, действующей на тело.
5) Объём погружённой части тела равен четверти объёма этого тела.
Запишем первый закон Ньютона для тела и шарика: [F_{text{Арх Т}}-m_{text{Т}}g-T=0] [F_{text{Арх Ш}}-m_{text{Ш}}g+T=0]
Сложим два уравнения: [F_{text{Арх Т}}-m_{text{Т}}g+F_{text{Арх Ш}}-m_{text{Ш}}g=0]
Обозначим плотность жидкости (rho_1), плотность материала (rho_2=2rho_1) [rho_1gV_1-rho_2cdot frac{1}{4}V_{T} g+rho_1 g cdot frac{1}{4} V_{T}-rho_2cdot frac{1}{4} V_{T} g=0] [rho_1V_1-2rho_1cdot frac{1}{4}V_{T} +rho_1 cdot frac{1}{4} V_{T}-2rho_1cdot frac{1}{4} V_{T} =0] [V_1-2cdot frac{1}{4}V_{T} + frac{1}{4} V_{T}-2cdot frac{1}{4} V_{T} =0] [V_1=frac{3}{4}V_T]
Тело плавает, погруженное на 3/4 своего объёма.
1) Сила Архимеда, действующая на тело, равна (displaystyle F_{text{Арх Т}}=rho_1gfrac{3}{4}V_T), а сила Архимеда, действующая на шар (displaystyle F_{text{Арх Т}}=rho_1gfrac{1}{4}V_T).
Утверждение 1 – (color{red}{small text{Неверно}})
2) [T=m_{text{Ш}}g-F_{text{Арх Ш}}]
Утверждение 2 – (color{red}{small text{Неверно}})
3) [T=F_{text{Арх Т}}-m_{text{Т}}g]
Утверждение 3 – (color{green}{small text{Верно}})
4) Модуль силы тяжести тела:[m_{text{Т}}g=rho_2cdot frac{1}{4}V_{T}g] Модуль силы тяжести шарика: [m_{text{Ш}}g=rho_2cdot frac{1}{4}V_{T}g]
Утверждение 4 – (color{green}{small text{Верно}})
5) Объём погружённой части тела равен (dfrac{3}{4}) объёма этого тела.
Утверждение 5 – (color{red}{small text{Неверно}})
Ответ: 34
Ученик помещал цилиндр, не удерживая его, в различные жидкости, плотности которых представлены в таблице, и измерял объем погруженной в жидкость части цилиндра (V_text{ погр}). По результатам измерений он получил зависимость, представленную на графике объема погруженной части цилиндра (V_text{погр}) от плотности жидкости (rho). Объем цилиндра постоянен и равен (V=10) см(^3)
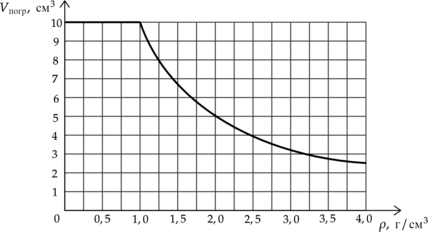[begin{array}{|c|c|c|c|c|c|c|c|}
hline
text{Жидкость}&text{Бензин}&text{Спирт}&text{Вода}&text{Глицирин}&text{Хлороформ}&text{Бромоформ}&text{Дийодметан}\
hline
text{Плотность $rho$ г/см$^3$}&0,71&0,79&1,0&1,26&1,49&2,89&3,25\
hline
end{array}]
На основании анализа приведённого графика выберите два верных утверждения и укажите в ответе их номера.
1) В бензине и воде сила Архимеда, действующая на цилиндр, одинакова.
2) Цилиндр не тонет в глицерине.
3) На цилиндр, погруженный в бромоформ, действует сила Архимеда 200мН.
4) Цилиндр плавает во всех жидкостях, указанных в таблице.
5) При плавании цилиндра в глицирине и бромоформе сила Архимеда, действующая на него, одинакова.
1) В бензине и в спирте цилиндр погружен на одинаковый объем. В таком случае сила Архимеда равна [F_A=rho gV_text{погр},] где (rho) – плотность жидкости, в которую погружено тело.
Но плотность спирта больше плотности бензина, а значит и сила Архимеда, действущая на цилиндр в спирте, больше силы Архимеда, действующей на цилиндр в бензине.
Утверждение 1 – (color{red}{small text{Неверно}})
2) Цилиндр тонет при плотности меньше, чем 1 г/см(^3), у глицирина плотность 1,26 г/см(^3), значит, цилиндр плавает.
Утверждение 2 – (color{green}{small text{Верно}})
3) У бромоформа плотность больше 1 г/см(^3), а значит сила Архимеда уравновешивает силу тяжести.
По графику видим, что цилиндр начинает плавать при плотности жидкости 1г/см(^3), а значит именно такова плотность материала, из которого он сделан. Откуда сила Архимеда, действующая на цилиндр [F_A=mg=1text{ г/см$^3$}cdot 10text{ см$^3$}cdot 10text{ Н/кг}=100text{ мН}] Утверждение 3 – (color{red}{small text{Неверно}})
4) Нет, при плотности меньше 1 г/см3 цилиндр не плавает.
Утверждение 4 – (color{red}{small text{Неверно}})
5) У глицирина и бромоформа плотность больше 1 г/см(^3), а значит сила Архимеда уравновешивает силу тяжести и силы Архимеда одинаковы.
Утверждение 5 – (color{green}{small text{Верно}})
Ответ: 25
На полу лифта расположены два одинаковых металлических бака, в которых доверху налита вода (см. рисунок).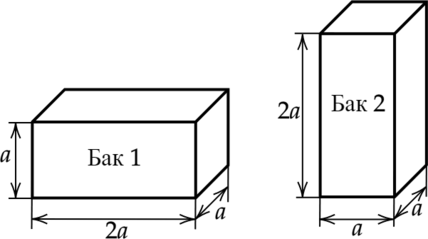 
Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
1) Давление воды на дно первого бака в 4 раза меньше, чем на дно второго.
2) Первый бак давит на пол лифта с силой, в 2 раза меньшей, чем второй.
3) Сила давления воды на дно первого бака в 2 раза меньше, чем на дно второго.
4) Первый бак оказывает на пол лифта в 2 раза меньшее давление, чем второй.
5) Если лифт начнёт движение вниз с ускорением 2 м/с(^2), давление воды на дно баков уменьшится на 20 %.
1) Давление воды на дно первого бака равно [displaystyle p_1=frac{mg}{2a^2}] где (m) — масса воды. Давление на дно второго бака [displaystyle p_2=frac{mg}{a^2}] Видно, что давление (p_2=2p_1), следовательно, давление воды на дно первого бака в 2 раза меньше, чем на дно второго бака.
Утверждение 1 – (color{red}{small text{Неверно}})
2) Сила давления равна силе тяжести воды. Так как объем одинаковый, значит масса воды в сосудах одинаковая.
Утверждение 2 – (color{red}{small text{Неверно}})
3) Утверждение 3 – (color{red}{small text{Неверно}})
4) Утверждение 4 – (color{green}{small text{Верно}})
5) При движении лифта вниз с ускорением 2 м/с(^2), оно будет компенсировать ускорение свободного падения (g), то есть вода будет иметь ускорение свободного падения 10-2=8 м/с(^2). В результате сила давления на дно баков будет равна (F=8m).
Утверждение 5 – (color{green}{small text{Верно}})
Ответ: 45
В сосуд с жидкостью погружают маленький датчик манометра, который регистрирует давление, создаваемое только столбом жидкости (без учёта атмосферного давления). На рисунке представлен график зависимости показаний (p) этого датчика давления от времени (t). Известно, что датчик может либо двигаться строго по вертикали вниз со скоростью 1 мм/с, либо покоиться. 
На основании анализа приведённого графика выберите два верных утверждения и укажите в ответе их номера.
1) Максимальная глубина погружения датчика давления равна 20 см.
2) В промежутке времени от 50 с до 150 с датчик давления находился на одной и той же глубине.
3) Плотность жидкости, в которую опустили датчик давления, равна 650 кг/м(^3).
4) Максимальная глубина погружения датчика давления равна 15 см.
5) Плотность жидкости, в которую опустили датчик давления, равна 1300 кг/м(^3).
1) Датчик двигался на промежутках от 0 с до 50 с и от 150 с до 200 с, т. е. глубина погружения (h=1 cdot (50 + 50 ) = 100) мм(= 10) см.
Утверждение 1 – (color{red}{small text{Неверно}})
2) Из графика видно, что давление не изменяется в промежутке времени от 50 с до 150 с, это означает что датчик находился на одной и той же глубине, т. е. покоился.
Утверждение 2 – (color{green}{small text{Верно}})
3) Давление столба жидкости: [p=rho gh] Плотность жидкости: [rho=frac{p}{gh}=frac{p}{gupsilon t}=frac{650}{10cdot0,001cdot50}=1300 text{ кг/м$^3$}]
Утверждение 3 – (color{red}{small text{Неверно}})
4) Глубина погружения 10 см
Утверждение 4 – (color{red}{small text{Неверно}})
5) Плотность жидкости (rho=1300) кг/м(^3)
Утверждение 5 – (color{green}{small text{Верно}})
Ответ: 25
Источник
Основы гидродинамики
Для успешного решения задания № 5 требуется знание основ гидродинамики. К ним относится понимание процессов, происходящих с жидкостями и телами, контактирующими с жидкостями, сущности физ.величин плотности и давления, а также формул, связывающих их с другими физ.величинами. Необходимая для решения задач такого плана информация имеется в разделе теории.
Теория к заданию №5 ОГЭ по физике
Плотность вещества
Плотностью называют массу вещества, которая приходится на единицу объема. Следовательно, плотностью можно считать удельную массу вещества. Количественно плотность определяют по формуле:
где m – массе вещества, V – его объем.
По этой же формуле вычисляется и средняя плотность. Для расчета при этом берется масса всего вещества и его общий объем.
Давление
Давлением называется: 1) сила, которая воздействует на поверхность твердого тела; 2) степень (сила) упругости жидкости либо газа. По сути, давление – это мера механического напряжения. Эта физ.величина является скалярной.
Давление в физике традиционно обозначается лат.буквой р. Единица измерения давления – паскаль (Па).
Атмосферное давление – это сила воздействия атмосф.столба на все физ.объекты (тела), находящиеся в атмосфере Земли, а также на земную поверхность. Если атмосфера является стационарной и покоящейся, то атмосф.давление на материальный объект соответствует весу столба воздуха над этим объектом, приходящегося на единицу площади. Атмосф.давление измеряется в мм ртутного столба (мм рт.ст.). Нормальным принято давление в 760 мм рт. ст. при t=0ºC. В пересчете на единицы СИ это давление соответствует 101325Па.
Сила Архимеда
На помещенное в жидкость физ.тело воздействует выталкивающая сила, равная по величине силе тяжести, испытываемая этим телом. Причина возникновения архимедовой силы – неодинаковость гидростатического давления в жидкости на различных глубинах. Точка ее приложения называется центром давления, который является центром масс тела (или его части) погруженного в жидкость
Формула для вычисления силы Архимеда:
где ρж – плотность жидкости; V – объем части физ.тела, помещенной в жидкость, или всего тела, если оно погружено в жидкость полностью.
Сообщающиеся сосуды
Сообщающимися считаются сосуды, которые объединены ниже поверхности жидкости в единую систему, причем так, что жидкость может перетекать из одного в другой.
Закон сообщающихся сосудов:
что означает обратную пропорциональную зависимость высоты столбов жидкостей и их плотностей.
Если в сообщающихся сосудах находится жидкость однородная, то высота столбов свободной поверхности жидкости в них совпадает.
Разбор типовых вариантов заданий №5 ОГЭ по физике
Демонстрационный вариант 2018
Цилиндр 1 поочередно взвешивают с цилиндром 2 такого же объема, а затем с цилиндром 3, имеющим меньший объем (см. рисунок).
Максимальную среднюю плотность имеет цилиндр
- 1
- 2
- 3
- 1 и 3
Алгоритм решения:
- Анализируем условие и рисунок слева (цилиндры 1 и 2). Определяем соотношение плотностей цилиндров.
- Анализируем условие и рисунок справа (цилиндры 3 и 1). Делаем вывод относительно соотношения плотностей.
- Определяем цилиндр с максимальной плотностью.
Решение:
- Согласно условию: . Поскольку на весах слева цилиндр 1 перевешивает 2, то это значит, что . Тогда из уравнения следует, что .
- По условию . Поскольку весы справа уравновешены, то это значит, что массы цилиндров равны, и из уравнения для плотности следует: .
- Объединив неравенства (1) и (2), получим: . Отсюда: максимальная плотность у 3-го цилиндра.
Ответ: 3
Первый вариант (Камзеева, № 7)
Одно из колен U-образного манометра соединили с сосудом, наполненным газом (см. рис.). Атмосферное давление равно 760 мм рт.ст. Чему равно давление газа в сосуде? В качестве жидкости в манометре используется ртуть.
- 1160 мм рт.ст
- 500 мм рт.ст.
- 360 мм рт.ст.
- 100 рт.ст.
Алгоритм решения:
- Анализируем условие и рисунок. Делаем вывод о соотношении атмосф.давления и давления в сообщающихся сосудах.
- Определяем искомую величину давления газа.
- Фиксируем ответ.
Решение:
- На схеме показано, что уровень ртути в 1-м (левом) колене меньше, чем в среднем. Это означает, что атмосф.давление выше давления газа. На шкале на рисунке видно, что разница давлений составляет 40 см. рт. ст., то есть 400 мм. рт. ст.
- Имеющаяся разница давлений означает, что давление газа меньше на эту разницу по сравнению с атмосферным давлением, т.е.: p = 760 — 400 = 360 (мм. рт. ст.).
Ответ: 3
Второй вариант (Камзеева, № 10)
Имеются три сплошных шара одинаковой массы, но изготовленные из разных веществ – из алюминия, стали или свинца. Шары полностью погружают в воду. Выталкивающая сила со стороны воду имеет
- наибольшее значение для алюминиевого шара
- наибольшее значение для стального шара
- наибольшее значение для свинцового шара
- одинаковое значение для всех шаров
Алгоритм решения:
- Записываем табличные значения для плотности материалов шаров.
- Записываем уравнение з-на Архимеда.
- Анализируем уравнение и определяем соотношение для выталкивающей силы для шаров.
- Записываем ответ.
Решение:
- Плотности материалов шаров: ; ; .
- Согласно з-ну Архимеда, выталкивающая сила равна: . Поскольку по условию шары погружены в жидкость целиком, то V – полный объем шара.
- Т.к. во всех 3 случаях жидкость одна и та же (вода), то в уравнении совпадает для всех шаров. Соответственно, максимальная архимедова сила у того из них, который имеет наибольший объем. Объем выразим из формулы для плотности вещества: . Учитывая оговорку в условии о том, что у шаров одинаковая масса, делаем вывод: чем меньше плотность вещества шара, тем больше выталкивающая сила. Поскольку наименьшую плотность имеет алюминий, то именно на алюминиевый шар действует максимальная выталкивающая сила.
Ответ: 1
Третий вариант (Камзеева, № 12)
Сосуд частично заполнили водой и уравновесили на рычажных весах (см. рис.).
В первом случае в сосуд опустили пробковый шарик, во втором случае – стальной шарик. Нарушится ли равновесие весов?
- равновесие нарушится только в первом случае
- равновесие нарушится только во втором случае
- равновесие нарушится в обоих случаях
- в обоих случаях равновесие не нарушится
Алгоритм решения:
- Анализируем 1-й случай. Делаем вывод о положении весов.
- Анализируем 2-й случай. Делаем вывод о положении весов.
- Находим верный вариант ответа. Записываем его.
Решение:
- В 1-м случае – с пробковым шариком – шарик будет плавать на поверхности воды (т.к. пробковый материал легче воды). При этом, поскольку сосуд заполнен водой целиком, при опускании в нее шарика она по з-ну Архимеда частично выплеснется. Сила тяжести, действующая на шарик, равна весу выплеснувшейся воды, так что вес шарика компенсирует ее. Поэтому равновесие весов сохранится.
- Масса стального шарика больше, чем масса воды, которую он выплеснет из сосуда, погрузившись в нее. Это означает, сила тяжести больше веса выплеснувшейся воды, и под действием результирующей этих сил равновесие будет нарушено.
- Ситуация, при которой в 1-м случае равновесие не нарушается, а во 2-м нарушается, соответствует варианту ответа 2
Ответ: 2
Даниил Романович | ???? Скачать PDF |
Источник