В сосудах разной формы жидкости одинаковой плотности
- Главная
- Вопросы & Ответы
- Вопрос 4337692
Таня Масян
более месяца назад
Просмотров : 86
Ответов : 1
Лучший ответ:
Главный Попко
Давление на дно одинаково, а сила давления зависит отплощади дна, где больше площадь, там больше сила давления
более месяца назад
Ваш ответ:
Комментарий должен быть минимум 20 символов
Чтобы получить баллы за ответ войди на сайт
Лучшее из галереи за : неделю месяц все время
Другие вопросы:
Суррикат Мими
Помогите решить уравнение. Оно вроде простое, но что-то не получается.. Уравнение: – 169=0 Заранее спасибо!
более месяца назад
Смотреть ответ
Просмотров : 14
Ответов : 1
Онтонио Веселко
Состав и направление грузопотоков байкало амурской магистрали
более месяца назад
Смотреть ответ
Просмотров : 18
Ответов : 1
Главный Попко
Ь знак в слове вьюга показатель мягкости или разделительный ?
более месяца назад
Смотреть ответ
Просмотров : 15
Ответов : 1
Энджелл
Составить шесть предложений с обособленными приложениями распространёнными и нераспространенными
более месяца назад
Смотреть ответ
Просмотров : 7
Ответов : 1
Зачетный Опарыш
2^x=-1 х= ? 2^х=-8 х= ?
более месяца назад
Смотреть ответ
Просмотров : 5
Ответов : 1
Источник
Часть А содержит 30 заданий (А1 – А30). К каждому заданию дается 4 варианта ответа, из которых правильный только один.
Внимательно прочитайте каждое задание и предлагаемые варианты ответа. Отвечайте только после того, как вы поняли вопрос и проанализировали все варианты ответа.
Выбрав нужный вариант ответа под номером выполняемого вами задания (А 1–А 30), кликните мышкой в кружочке, соответствующем выбранному вами ответу.
Выполняйте задания в том порядке, в котором они даны. Если какое-то задание вызывает у вас затруднение, пропустите его. К пропущенным заданиям можно будет вернуться, если у вас останется время.
За выполнение каждого задания дается один балл. Баллы, полученные вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Желаем успеха!
Здесь приведены справочные данные, которые могут понадобиться вам при выполнении работы.
Полный перечень вопросов, которые могут контролироваться на едином государственном экзамене 2010 года, приведен в кодификаторе, помещённом на сайтах www.ege.edu.ru и www.fipi.ru.
A1. Действие гидравлического пресса основано на
законе Архимеда
законе Паскаля
законе сохранения импульса
законе Кулона
A2. С помощью гидравлического пресса можно получить выигрыш
в силе
в работе
в скорости
в давлении
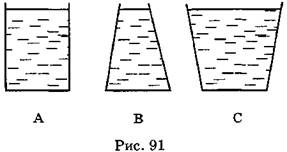A3. На рис. 91 изображены три сосуда разной формы с одинаковой площадью основания, в которые налита одинаковая жидкость. Верхний уровень жидкости в сосудах тоже одинаков. Сила давления на дно больше веса жидкости в сосуде
A
B
C
одинаковы во всех сосудах
A4. Единица давления в СИ может быть выражена через основные единицы СИ следующим образом:
кг•м•с-2
кг•м-1•с2
кг•м-1•с-2
кг•м2•с-2
A5. Верным является утверждение, что давление
векторная величина, равная произведению силы давления на ее плечо
скалярная величина, равная отношению силы давления к массе тела
векторная величина, равная произведению массы и скорости тела
скалярная величина, равная отношению силы давления к площади опоры
A6. В сообщающиеся сосуды налиты две разнородные жидкости (рис. 92). Плотность жидкости в левом колене равна 600 кг/м3. Плотность жидкости в правом колене равна
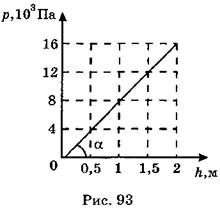
A7. На рис. 93 изображен график зависимости давления жидкости p от ее глубины h. Плотность этой жидкости равна
600 кг/м3
800 кг/м3
1000 кг/м3
1200 кг/м3
A8. Куб с длиной ребра 20 см плавает в воде, наполовину погруженным в нее. Плотность воды 1000 кг/м3. На куб действует выталкивающая сила, равная
40 Н
160 Н
80 Н
100 Н
A9. Труба имеет переменное сечение. Радиус ее широкой части 10 см, скорость воды в ней 4 м/с. Чему равна скорость воды в узкой части трубы радиусом 4 см?
25 м/с
40 м/с
20 м/с
16 м/с
A10. Вес тела в воздухе 400 Н, а в воде 320 Н. Плотность воды 1000 кг/м3. Объем тела равен
400 см3
4000 см3
8000 см3
7200 см3
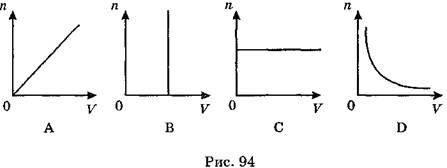
A11. Какой из графиков (рис. 94) правильно показывает зависимость концентрации молекул от объема газа при неизменном общем числе молекул?
A
B
C
D
A12. По мере сжатия газа
увеличиваются силы отталкивания между молекулами, а силы их взаимного притяжения уменьшаются
увеличиваются и силы отталкивания, и силы притяжения молекул друг к другу
увеличиваются силы притяжения молекул друг к другу, а силы их взаимного отталкивания уменьшаются
уменьшаются силы взаимного притяжения молекул, а силы их взаимного отталкивания остаются неизменными
A13. В баллон емкостью 10 л впустили 5 л кислорода, 4 л азота и 8 л водорода. Объем смеси этих газов стал равен
12 л
10 л
17 л
8 л
A14. Близким к идеальному является газ, находящийся
под высоким давлением и при низкой температуре
под низким давлением и при низкой температуре
под низким давлением и при высокой температуре
под высоким давлением и при высокой температуре
A15. На рис. 95 изохорному процессу соответствует график
A16. Под поршнем массой 2 кг с площадью основания 5 см2 находится газ. Поршень находится в состоянии равновесия. Атмосферное давление нормальное (105 Па). Чему равно давление газа под поршнем?
2•105 Па
0,8•105 Па
1•105 Па
1,4•105 Па
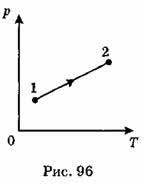A17. На рис. 96 показана зависимость давления данной массы идеального газа от его температуры. В этом процессе объем газа
увеличивался
уменьшался
не изменялся
нет однозначного ответа
А18. Температура газа 27 °С. Постоянная Больцмана 1,38•10-23Дж/К. Средняя кинетическая энергия молекул газа примерно равна
6,2•10-21Дж
3,7•10-22Дж
5,6•10-22Дж
2,6•10-23Дж
A19. В закрытом сосуде находится газ под давлением 200 кПа. Каким станет давление газа, если температуру повысить на 30% ?
170 кПа
260 кПа
320 кПа
400 кПа
A20. Относительная влажность воздуха 60%, давление насыщенного пара в нем при некоторой температуре равно 2,2 кПа. Чему равно парциальное давление пара при этой же температуре?
0,9 кПа
0,7 кПа
1,8 кПа
1,3 кПа
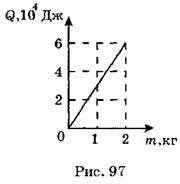A21. На рис. 97 показан график зависимости количества теплоты, необходимого для нагревания на 10 °С некоторого вещества, от его массы. Удельная теплоемкость этого вещества равна
600 Дж/(кг•К)
1200 Дж/(кг•К)
3000 Дж/(кг•К)
4200 Дж/(кг•К)
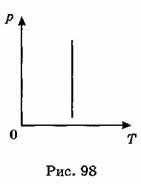
A22. На рис. 98 изображен график зависимости давления газа от его температуры. Газ получает от нагревателя количество теплоты 300 Дж. При этом
изменение его внутренней энергии равно нулю, а совершенная газом работа равна 300 Дж
изменение его внутренней энергии равно 300 Дж, а работы газ не совершает
внутренняя энергия газа уменьшается на 300 Дж, и газ совершает работу 300 Дж
внутренняя энергия газа увеличивается на 150 Дж, и газ совершает работу 150 Дж
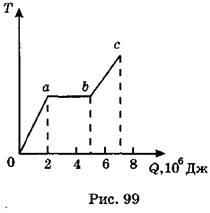
A23. На рис. 99 изображен график изменения температуры жидкости массой 1 кг в зависимости от переданного ей количества теплоты. Удельная теплота парообразования этой жидкости равна
5•106Дж/кг
7•106 Дж/кг
2•106 Дж/кг
3•106 Дж/кг
A24. Газ сжали, совершив 300 Дж работы, и он выделил во внешнюю среду 500 Дж теплоты. При этом его внутренняя энергия
увеличилась на 800 Дж
уменьшалась на 200 Дж
уменьшилась на 100 Дж
увеличилась на 400 Дж
A25. Под давлением 100 кПа данная масса газа изобарно расширилась, увеличив объем с 3 л до 9 л. При этом внутренняя энергия газа
увеличилась на 1800 Дж
увеличилась на 900 Дж
уменьшилась на 600 Дж
уменьшилась на 300 Дж
A26. Тело массой 5 кг упало с высоты 4 м. При этом 40% его механической энергии пошла на нагревание. Количество теплоты, полученное телом при нагревании равно
200 Дж
100 Дж
60 Дж
80 Дж
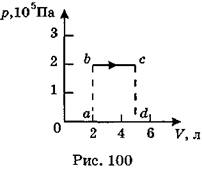A27. На рис. 100 изображен график изобарного расширения газа в координатах р – V, вследствие передачи ему извне 900 Дж теплоты. При этом внутренняя энергия газа
увеличилась на 300 Дж
увеличилась на 500 Дж
уменьшилась на 400 Дж
уменьшилась на 100 Дж
A28. При изотермическом сжатии идеального газа его внутренняя энергия
увеличивается
не изменяется
уменьшается
может увеличиваться или уменьшаться в зависимости от скорости сжатия
A29. Двигатель внутреннего сгорания автомобиля имеет наибольший КПД
летом
осенью
зимой
весной
A30. КПД идеального теплового двигателя 60 % , температура внешней среды 27 °С. Температура его нагревателя равна
350 К
750 К
1050 К
3000 К
Источник
Определение
Соединенные между собой сосуды называют сообщающимися.
В таких сосудах жидкость имеет возможность перетекать из одной емкости в другую (рис.1). Форма сообщающихся сосудов может быть самая разная.
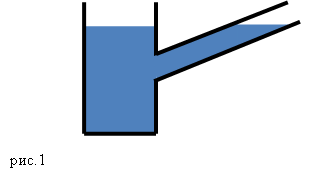
Допустим, что в сообщающиеся сосуды налита однородная жидкость, то в этих сосудах жидкость устанавливается на одном уровне, если давление над поверхностью жидкости одинаково, и не важно какую форму имеют сосуды. В неподвижной жидкости давление ($p$) на одном уровне в сообщающихся сосудах является равным, так как мы знаем, что:
[p=rho gh left(1right),]
где $rho $ – плотность жидкости; $g$ – ускорение свободного падения; $h$ – высота столба жидкости. Так как давление на одном уровне жидкости одинаково, то равными будут и высоты столбов жидкости.
Жидкости разной плотности в сообщающихся сосудах
Допустим, что в сообщающиеся сосуды налили жидкость разной плотности (рис.2(б)). В состоянии равновесия жидкостей, их уровни не будут находиться на одном уровне (высоты столбов жидкости равными не будут).
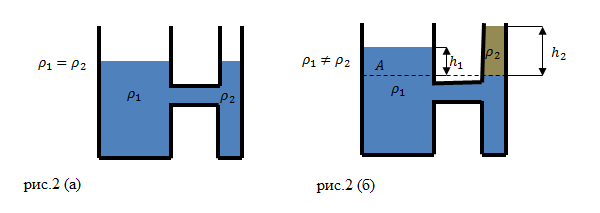
Жидкости в сосудах находятся в равновесии. Давления на уровне A (граница раздела разных жидкостей) (рис. 2 (б)) равны:
[{rho }_1gh_1={rho }_2gh_2left(2right),]
где ${rho }_1$ и ${rho }_2$ – плотности жидкостей. Найдем отношение высот столбов жидкостей в сосудах:
[frac{h_1}{h_2}=frac{{rho }_2}{{rho }_1}left(3right).]
Формула (3) говорит о том, что в сообщающихся сосудах высоты столбиков жидкости над уровнем их раздела обратно пропорциональны плотностям этих жидкостей. При одинаковом давлении над поверхностями жидкостей, высота столба жидкости с меньшей плотностью будет больше, чем высота столба более плотной жидкости.
Гидравлический пресс и другие примеры использования сообщающихся сосудов
В технике сообщающиеся сосуды используют часто. Например, существует такое устройство, как гидравлический пресс. Его изготавливают из двух цилиндров разного радиуса, в которых находятся поршни (рис.3). Сообщающиеся сосуды пресса обычно заполняют минеральным маслом.
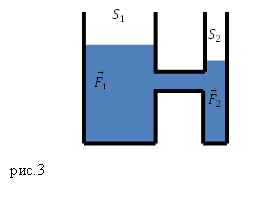
Пусть площадь первого поршня, к которому прикладывают силу ${overline{F}}_1,$ равна $S_1$, площадь второго $S_2$, к нему приложена сила ${overline{F}}_2$. Давление, которое создает первый поршень равно:
[p_1=frac{F_1}{S_1}left(4right).]
Второй поршень давит на жидкость:
[p_2=frac{F_2}{S_2}left(5right).]
Если система находится в состоянии равновесия, то по закону Паскаля давления $p_1$ и $p_2$ равны:
[frac{F_1}{S_1}=frac{F_2}{S_2}left(6right).]
Получим:
[F_1=F_2frac{S_1}{S_2}(7)]
величина первой силы больше модуля силы $F_2$ в $frac{S_1}{S_2}$ раз. Это означает, что при помощи гидравлического пресса, прикладывая небольшую силу к поршню малого сечения, можно получить большую по величине силу, которая будет действовать на большой поршень.
По принципу сообщающихся сосудов, в особенности раньше, действовал водопровод. Такой водопровод сейчас еще можно наблюдать на дачных участках. На относительно большой высоте устанавливается бак с водой, от бака идут водопроводные трубы, закрываемые кранами. Давление у кранов соответствует давлению столба воды, который равен разности высот уровень крана – уровень воды в баке.
Принципом сообщающихся сосудов пользовались, когда проектировали фонтаны, работающие без насосов, шлюзы на реках и каналах.
Примеры задач с решением
Пример 1
Задание. Имеются два цилиндрических сосуда. Высота столба жидкости в одном равна $h_1$, в другом $h_2$. Эти сосуды соединяют трубкой. Насколько изменится высота столба жидкости в левом сосуде, если площадь поперечного сечения его $S_1>S_2$ , $S_2$ – площадь сечения правого сосуда. Объемом трубки пренебречь.
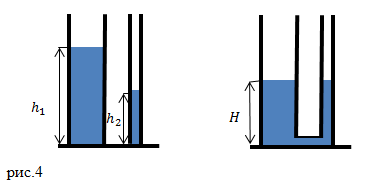
Решение. После того как сосуды соединили, они стали сообщающимися. Часть жидкости из левого сосуда перетечет в правый. Так как жидкость в правом и левом сосудах одна и та же, то уровни жидкости в обоих сосудах будут находиться на одном уровне, то есть высота столбиков жидкости станет равна $H$ в обоих коленах емкости. Определим, какой объем воды перетечет из левого колена в правое:
[Delta V_1=left(h_1-Hright)S_{1 }left(1.1right),]
где $S_{1 }$ – площадь поперечного сечения левого сосуда (сосуда из которого вытекает жидкость). В правом сосуде эта жидкость займет объем равный:
[Delta V_2=left(H-h_2right)S_{2 }left(1.2right),]
где $S_{2 }$ – площадь поперечного сечения правого сосуда. Так как мы считаем, что жидкость не сжимаема, то имеем:
[Delta V_1=Delta V_2left(1.3right).]
Приравниваем правые части выражений (1.2) и (1.1), выражаем высоту столбиков жидкости в правой и левой части сообщающихся сосудов:
[left(h_1-Hright)S_{1 }=left(H-h_2right)S_{2 }to H=frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }} left(1.4right).]
Используя выражение (1.4), изменение высоты жидкости в левом колене, получим равным:
[Delta h=h_1-H=h_1-frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }}=frac{h_1S_1+h_1S_2-h_1S_{1 }-S_{2 }h_2}{S_1+S_{2 }}=]
[=frac{h_1S_2-S_{2 }h_2}{S_1+S_{2 }}=frac{h_1-h_2}{S_1+S_{2 }}S_2.]
Ответ. $Delta h=frac{h_1-h_2}{S_1+S_{2 }}S_2$
Пример 2
Задание. Какой будет сила давления на большой поршень (площадью $S_1$) гидравлического пресса, если площадь его малого поршня равна $S_2$, при этом на него действует сила равная $F_2$?
Решение. В теоретическом разделе сказано, что гидравлический пресс представляет собой систему из сообщающихся сосудов (рис.3). Из закона Паскаля следует, что, прикладывая небольшую силу ($F_2$) к поршню малого сечения ($S_2$) пресса, можно получить большую по величине силу, которая будет действовать на большой поршень ($S_1$):
[F_1=F_2frac{S_1}{S_2}(2.1)]
Ответ. $F_1=F_2frac{S_1}{S_2}$
Читать дальше: условия плавания тел.
Источник