В сосуде 11 шаров
Из
60 вопросов, входящих в экзаменационные
билеты, студент подготовил 50. Какова
вероятность того, что вытянутый студентом
билет, содержащий два вопроса, будет
состоять из подготовленных им вопросов?
Задание
2
В
сосуде находится 11 шаров, из которых 4
цветных и 7 белых. Найти вероятность
двукратного извлечения из сосуда
цветного шара:
а)
если вынутый шар возвращается обратно
в сосуд;
б)
если вынутый шар в сосуд не возвращается.
Задание
3
Трое
рабочих обрабатывают однотипные детали.
Первый обработал за смену 20 деталей,
второй – 25, третий – 15. Вероятность
брака для первого рабочего равна 0,03,
для второго – 0,02, для третьего – 0,04. Из
общей выработки за смену наудачу взята
и проверена одна деталь, которая оказалась
бракованной. Найти вероятность того,
что она обработана вторым рабочим.
Задание
4
Вероятность
того, что деталь окажется бракованной,
равна p =
0,3. Составить ряд распределения для
случайной величины X,
представляющей собой число бракованных
деталей в выборке объема n =
4. Определить вероятность того, что в
выборке будет:
а)
ровно k =
2 бракованных деталей;
б)
не более k =
2 бракованных деталей;
в)
ни одна деталь не бракованная.
Найти
функцию распределения F(x),
математическое ожидание M(x),
дисперсию D(x).
Задание
5
Случайная
величина X задана
функцией распределения F(x):
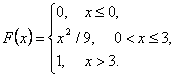Найти:
1)
плотность распределения вероятностей f(x);
2)
математическое ожидание;
3)
построить графики функций f(x), F(x).
Задание
6
Требуется
найти вероятность попадания в заданный
интервал (4, 8) нормально распределенной
случайно величины, если известны ее
математическое ожидание m =
5 и среднее квадратическое отклонение =
3.
Задание
7
Известны x1, x2,
…, xn –
результаты независимых наблюдений над
случайной величиной X.
50 | 52 | 140 | 138 | 165 | 165 | 210 | 165 | 170 | 142 | 150 | 168 |
103 | 63 | 68 | 88 | 85 | 105 | 110 | 112 | 131 | 125 | 126 | 135 |
148 | 92 | 99 | 102 | 110 | 115 | 118 | 125 | 121 | 118 | 130 | 133 |
141 | 182 | 199 | 205 | 127 | 132 | 135 | 98 | 105 | 119 | 115 | 125 |
124 |
1)
Сгруппировать эти данные в интервальную
таблицу, подобрав длину интервала или
воспользовавшись заданной длиной
интервала.
2)
Построить гистограмму и эмпирическую
функцию распределения.
3)
Найти несмещенные оценки для математического
ожидания и дисперсии случайной величины X.
4)
По критерию Пирсона проверить гипотезу
о том, что случайная величина Xимеет
нормальный закон распределения.
5)Найти
интервальные оценки математического
ожидания и среднего квадратического
отклонения случайной величины X с
уровнем доверия 0,99
Вариант №5
Задание
1
Среди
17 студентов группы, из которых 8 девушек,
разыгрывается 7 билетов. Какова вероятность
того, что среди обладателей билетов
окажутся 4 девушки?
Задание
2
От
группы студентов, состоящей из 14 юношей
и 11 девушек, на профсоюзную конференцию
выбирается два человека. Какова
вероятность того, что среди выбранных
будет хотя бы одна девушка?
Задание
3
Радиолампа
может принадлежать к одной из трех
партий с вероятностью P1,P2, P3,
где P1 = P2 =
0,25, P3 =
0,5. Вероятность того, что радиолампа
проработает заданное число часов, равна
соответственно 0,1; 0,2; 0,4. Определить
вероятность того, что радиолампа
проработает заданное число часов.
Задание
4
Вероятность
того, что деталь окажется бракованной,
равна p =
0,3. Составить ряд распределения для
случайной величины X,
представляющей собой число бракованных
деталей в выборке объема n =
5. Определить вероятность того, что в
выборке будет:
а)
ровно k =
4 бракованных деталей;
б)
не более k =
4 бракованных деталей;
в)
ни одна деталь не бракованная.
Найти
функцию распределения F(x),
математическое ожидание M(x),
дисперсию D(x).
Задание
5
Случайная
величина X задана
функцией распределения F(x):
Найти:
1)
плотность распределения вероятностей f(x);
2)
математическое ожидание;
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
При работе со своими учениками, у меня накапливается много задач. Поэтому я публикую разборы задач в свободный доступ, стараюсь делать это максимально подробно и понятно, чтобы начинающие могли прочитать и разобраться в нужной для них теме. Ну а за подробными индивидуальными консультациями и репетиторством вы можете написать в мою группу в вк или в личные сообщения. Также большое количество разборов задач вы сможете найти в моей группе Репетитор IT mentor
Задача 1. На тело массой 100 кг, лежащее на наклонной плоскости, которая образует с горизонтом угол 40°, действует горизонтальная сила 1500 Н. Определить:
1) силу, прижимающую тело к плоскости;
2) силу трения тела о плоскость;
3) ускорение, с которым поднимается тело. Коэффициент трения k = 0.10; g = 10м/с².
Задача 2. Тело движется по горизонтальной плоскости под действием силы F, направленной под углом α к горизонту. Найти ускорение тела, если на него действует сила тяжести P, а коэффициент трения между телом и плоскостью равен k . При какой величине силы F движение будет равномерным.
Задача 3. Два шара массами m1 = 2.5 кг и m2 = 1.5 кг движутся навстречу друг другу со скоростями v1 = 6 м/c и v2 = 2 м/c . Определить: 1) скорости шаров после удара; 2) кинетические энергии шаров до и после удара; 3)энергию, затраченную на деформацию шаров при ударе. Удар считать прямым, неупругим.
Прикрепляю очередной разбор задачи по физике по теме закона сохранения импульса. Неупругие шары после удара не восстанавливают свою первоначальную форму. Таким образом, сил, которые отталкивали бы шары друг от друга, не возникает. Это значит, что после удара шары будут двигаться вместе (слипшись) с одной и той же скоростью . Эту скорость определим по закону сохранения импульса. Так как шары двигаются по одной прямой, то можно записать импульс системы до удара и после удара. Считаем, что в задаче не действует диссипативных сил (сил трения, сопротивления воздуха и т.д.), поэтому импульс вдоль оси Ox сохраняется, тогда (смотри решение на картинке). Расписал довольно подробно, но если что-то не будет понятно, то задавайте вопросы в комментариях.
Задача 4. Диск массой m, радиус которого R , вращается с угловой скоростью ω0 вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. После прекращения действия на него силы диск останавливается в течение времени t. Определить угловое ускорение диска и тормозящий момент, действующий на него.
Задача 5. Два тела массами m1 и m2 связаны нитью, перекинутой через блок массой M . Найти ускорение тел, считая блок сплошным диском.
Задача 6. Шар катится по горизонтальной поверхности со скоростью v . На какую высоту h относительно своего первоначального положения поднимется шар, если он начнет вкатываться на наклонную плоскость без проскальзывания?
Задача 7. На краю вращающейся с угловой скоростью ω0 платформе стоит человек массой m. После того, как человек перешёл в другую точку платформы, угловая скорость её вращения стала равной ω. Найти расстояние от оси вращения до человека, считая платформу диском массой M и радиусом R.
Задача 8. Тело массой m брошено со скоростью v0 под углом α к горизонту. Найти кинетическую и потенциальную энергию тела в высшей точке траектории.
Задача 9. На горизонтальной поверхности находятся два тела массами m1 = 10 кг и m2 =15 кг, связанные нитью. К телу массой m2 прикладывают силу F = 100 Н, направленную под углом α = 60° к горизонту. Определить ускорение грузов и силу натяжения нити, соединяющей грузы. Трением пренебречь. (обязательно указать все силы на чертеже!)
Задача 10. На поверхности стола лежит груз массой m2 = 2 кг. На нити, прикрепленной к грузу m2 и перекинутой через невесомый блок, подвешен груз m1 = 1 кг. Коэффициент трения груза о поверхность стола 0,2. Найти ускорение грузов и силу натяжения нити.
Задача 11. Лодка массой 200 кг и длиной 3 м стоит неподвижно в стоячей воде. Мальчик массой 40 кг в лодке переходит с носа на корму. Определите, на какое расстояние при этом сдвинется лодка.
Считаем, что в нашей задаче не действует внешних сил, поэтому по теореме о центре массы системы грузов, можно считать, что координаты центра масс сохраняются в проекциях на ось OX (по оси OY движения не происходит). Проведем ось Y(ноль оси X) через центр лодки, тогда можно записать координаты человека и лодки до перехода человека с носа на корму.
Задача 12. Шарик массой 5 кг подвешен на нити. Нить может выдержать максимальное натяжение 100 Н. На какой минимальный угол от положения равновесия нужно отклонить нить с шариком, чтобы он оборвал нить, проходя через положение равновесия? (обязательно сделать рисунок, указать действующие силы!)
Задача 13. Два неупругих шара массами m1=2 кг и m2=3 кг движутся со скоростями соответственно v1=8 м/c и v2=4м/с. Определить количество теплоты, выделившееся при их столкновении. Рассмотреть 2 случая: 1) шары движутся навстречу друг другу; 2) меньший шар догоняет больший.
Задача 14. Тело совершает гармонические колебания по закону x(t) = 50⋅sin(π/3⋅t) (см). Определить полную энергию тела, если его масса 0,2 кг. Какая сила действует на тело в момент времени t = 0,5 с?
Задача 15. Два математических маятника, длины которых отличаются на Δℓ =16 см, совершают за одно и то же время: один − 10 колебаний, другой − 6 колебаний. Определить длины маятников.
Задача 16. Определить, сколько молей и молекул водорода содержится в объёме V = 5 м³ под давлением Р = 767 мм.рт.ст. при температуре t = 18 ° С. Какова плотность газа?
Задача 17. Сколько кислорода выпустили из баллона ёмкостью 1 дм3, если давление его изменилось от 14 атм до 7 атм, а температура от 27°С до 7 °С ?
Задача 18. В сосуде объёмом V = 2 м³ находится смесь m1 = 4 кг гелия и m2 = 2 кг водорода при температуре 27°С. Определить давление и молярную массу смеси газов.
Задача 19. В сосуде содержится смесь газов: гелия массой 12 г и водорода массой 2 г, температура в сосуде 77°С, давление 20 кПа. Определить молярную массу и плотность смеси газов.
Задача 20. Гелий массой 20 г нагрели от 100°С до 400°С, причем газу была передана теплота 30 кДж. Найти изменение внутренней энергии гелия и совершенную им работу.
Задача 21. При изотермическом расширении от 0,1 м3 трех молей газа его давление меняется от 4,48 атм до 1 атм. Найти совершаемую при этом работу и температуру, при которой протекает процесс.
Задача 22. Моль идеального газа, имевший первоначально температуру 300ºК, расширяется изобарически до тех пор, пока его объем не возрастет в 3 раза. Затем газ охлаждается изохорически до первоначальной температуры. Определить суммарное получаемое газом количество теплоты. Обязательно нарисовать графики процессов.
Задача 23. Азот массой m = 1 кг занимает при температуре Т1 = 300 К объём V = 0,5 м³. В результате адиабатного сжатия давление газа увеличилось в 3 раза. Определить конечный объём газа и конечную температуру.
Задача 24. Газ расширяется адиабатически, причём объём его увеличивается вдвое, а термодинамическая температура падает в 1,32 раза. Какое число степеней свободы i имеют молекулы этого газа?
Задача 25. Баллон ёмкостью V = 20 л с кислородом при давлении Р = 107 Па и температуре t1 = 70 ºС нагревается до температуры t2 = 270 ºС. Какое количество теплоты при этом поглощает газ?
Задача 26. Азот, занимающий при давлении, равном Р1 = 10⁵ Па объём V1 = 10 л, расширяется вдвое. Найти конечное давление и работу, совершённую газом в процессах: а) изобарном; б) изотермическом; в) адиабатном.
Задача 27. Кислород, масса которого 200 г, нагревают от температуры Т1 =300 К до Т2 = 400 К. Найти изменение энтропии, если известно, что начальное и конечное давление газа одинаковы и близки к атмосферному.
Задача 28. Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 1,5∙10⁵ Дж. Температура нагревателя Т1 = 400 К, температура холодильника Т2 = 260 К. Найти КПД машины, количество теплоты Q1, получаемое машиной за один цикл от нагревателя, и количество теплоты Q2, отдаваемое за один цикл холодильнику.
Задача 29. Найти суммарную кинетическую энергию Е поступательного движения всех молекул, содержащихся в объёме V = 1 дм³ газа при атмосферном давлении.
Задача 30. Чему равны средние кинетические энергии поступательного и вращательного движения молекул, содержащихся в 100 г водорода при температуре 400 К ? Чему равна полная внутренняя энергия газа?
Спасибо, что дочитали до конца, дорогие подписчики 🙂 Если вам интересен подобный контент и разборы задач, то оставляйте обратную связь в виде лайков и комментариев.
Еще много полезного и интересного вы сможете найти на ресурсах:
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Репетитор IT mentor в Telegram
Physics.Math.Code в контакте (VK)
Physics.Math.Code в telegram
Physics.Math.Code в YouTube
Источник
Следствием теорем сложения и умножения является формула полной вероятности.
Допустим, что предполагается провести опыт, об условиях которого можно сделать n исключающих друг друга предположений (гипотез) ,, причем .
Вероятность некоторого события A, которое может появиться только вместе с одной из гипотез, вычисляется по формуле
.
Эта формула носит название формулы полной вероятности..
Получить решение
Если же событие A совершилось и необходимо найти вероятность того, что оно произошло совместно с некоторой гипотезой , то необходимо воспользоваться формулой Бейеса
.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПРИМЕР 13.2.30. Имеются три одинаковые на вид урны; в первой 2 белых и 3 черных шара, во второй – 4 белых и 1 черный шар, в третьей – 3 белых шара. Наугад выбирается одна из урн и из нее вынимается один шар. Найти вероятность того, что этот шар будет белым.
Решение. Опыт предполагает 3 гипотезы:
выбор первой урны; ;
выбор второй урны; ;
выбор третьей урны; .
Рассмотрим интересующее нас событие.
A — вынутый шар белый. Данное событие может произойти только с одной из гипотез .
Тогда .
ПРИМЕР 13.2.31. Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60% деталей отличного качества, а второй – 84%. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь произведена первым автоматом.
Решение. Можно сделать два предположения (гипотезы):
деталь произведена первым автоматом, причем (поскольку первый автомат производит вдвое больше деталей, чем второй) ;
деталь произведена вторым автоматом, причем .
Условная вероятность того, что деталь будет отличного качества, если она произведена первым автоматом , если произведена вторым автоматом .
Вероятность того, что наудачу взятая деталь окажется отличного качества, по формуле полной вероятности равна
.
Искомая вероятность того, что взятая отличная деталь произведена первым автоматом, по формуле Бейеса равна
.
ПРИМЕР 13.2.32. Два стрелка независимо друг от друга стреляют по одной и той же мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,8, для второго – 0,4. После стрельбы в мишени обнаружена одна пробоина. Найти вероятность того, что эта пробоина принадлежит первому стрелку (исход «обе пробоины совпали» отбрасываем, как ничтожно маловероятный).
Решение. До опыта возможны следующие гипотезы:
ни первый, ни второй стрелки не попадут;
оба стрелка попадут;
первый стрелок попадет, а второй – нет;
первый стрелок не попадет, а второй попадает.
Доопытные (априорные) вероятности гипотез:
,
,
,
.
Условные вероятности осуществленного события A — в мишени одна пробоина, при этих гипотезах равны:
.
После опыта гипотезы и становятся невозможными, а послеопытные (апостериорные) вероятности гипотез и по формуле Бейеса будут
; .
Примеры и задачи для самостоятельного решения
Решить задачи, используя формулу полной вероятности и формулу Бейеса
13.2.5.1. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника – 0,9, для велосипедиста – 0,8 и для бегуна – 0,75. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит норму.
Отв.:0,86
13.2.5.2. Из урны, содержащей 5 белых и 3 черных шара, извлекается наудачу один шар и перекладывается в другую урну, которая до этого содержала 2 белых и 7 черных шаров. Цвет перекладываемого шара не фиксируется. Из второй урны наудачу извлекается один шар. Какова вероятность, что этот шар окажется белым?
Отв.:21/80
13.2.5.3. В урну, содержащую шаров, опущен белый шар, после чего наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров (по цвету).
Отв.:(n+2)/(2(n+1))
13.2.5.4. В условиях предыдущей задачи из урны был извлечен белый шар. Найти вероятность того, что в урне было белых шаров.
Отв.:2(m+1)/((n+1)(n+2))
13.2.5.5. В пирамиде 5 винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом равна 0,95; для винтовки с обычным прицелом эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки.
Отв.:0,85
13.2.5.6. В условиях предыдущей задачи стрелок попал в мишень. Определить вероятность того, что он стрелял а) из винтовки с оптическим прицелом; б) из винтовки с обычным прицелом.
Отв.:а)57/85; б)28/85
13.2.5.7. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы курса 4, из второй – 6, из третьей группы – 5 студентов. Вероятности того, что студент первой, второй и третьей группы попадает в сборную института, соответственно равны 0,9; 0,7 и 0,8. Наудачу выбранный студент в итоге соревнования попал в сборную. К какой из групп вероятнее всего принадлежал этот студент?
Отв.:18/59;21/59;20/59
13.2.5.8. Из полного набора 28 костей домино наудачу извлечена кость. Найти вероятность того, что вторую извлеченную наудачу кость можно приставить к первой.
Отв.:7/18
13.2.5.9. В первой урне содержится 10 шаров, из них 8 белых; во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух шаров наудачу взят один шар. Найти вероятность того, что взят белый шар.
Отв.:0,5
13.2.5.10. Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин, проезжающих по тому же шоссе как 3:2. Вероятность того, что будет заправляться грузовая машина равна 0,1; для легковой машины эта вероятность равна 0,2. Найти вероятность того, что наудачу выбранная машина потребует заправки.
Отв.:
13.2.5.11. В условиях предыдущей задачи к бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.
Отв.:3/7
13.2.5.12. В группе из 10 студентов, пришедших на экзамен, 3 подготовлены на отлично, 4 – хорошо, 2 – посредственно, 1 – плохо. В экзаменационных билетах имеется 20 вопросов. Отлично подготовленный студент знает все 20 вопросов, хорошо подготовленный – 16 вопросов, посредственно подготовленный – 10 вопросов и двоечник – 5 вопросов. Вызванный наугад студент ответил на три произвольно заданных вопроса. Найти вероятность того, что этот студент подготовлен а) отлично; б) плохо.
Отв.:а)114/197; б)1/591
13.2.5.13. При отклонении от нормального режима работы автомата срабатывает сигнализатор С-1 с вероятностью 0,8, а сигнализатор С-11 срабатывает с вероятностью 1. Вероятности того, что автомат снабжен сигнализатором С-1 или С-11 соответственно равны 0,6 и 0,4. Получен сигнал о разделке автомата. Что вероятнее: автомат снабжен сигнализатором С-1 или С-11?
Отв.:P(С-1)= 6/11, Р(С-11)= 5/11
13.2.5.14. В каждой из трех урн содержится 6 черных и 4 белых шара. Из первой урны наудачу извлечен один шар и переложен во вторую урну, после чего из второй урны наудачу извлечен один шар и переложен в третью урну. Найти вероятность того, что шар, наудачу извлеченный из третьей урны, окажется белым.
Отв.:0,4
13.2.5.15. Имеется урн, в каждой из которых белых и черных шаров. Из первой урны во вторую перекладывается наудачу один шар, затем из второй в третью и так далее. Затем из последней урны извлекается один шар. Найти вероятность того, что он белый.
Отв.:a/(a+b)
13.2.5.16. По объекту производится три одиночных независимых выстрела. Вероятность попадания при первом выстреле равна 0,4; при втором – 0,5; при третьем – 0,7. Для вывода объекта из строя заведомо достаточно трех попаданий, при двух попаданиях он выходит из строя с вероятностью 0,6; при одном – с вероятностью 0,2. Найти вероятность того, что в результате трех выстрелов объект будет выведен из строя.
Отв.:0,458
13.2.5.17. Имеются три партии деталей по 20 деталей в каждой. Число стандартных деталей в первой, второй и третьей партиях соответственно равно 20, 15, 10. Из наудачу выбранной партии наудачу извлечена деталь, оказавшаяся стандартной. Деталь возвращают в партию и вторично из той же партии наудачу извлекают деталь, которая также оказывается стандартной. Найти вероятность того, что детали были извлечены из третьей партии.
Отв.:4/29
13.2.5.18. Три стрелка произвели залп, причем две пули поразили мишень. Найти вероятность того, что третий стрелок поразил мишень, если вероятности попадания в мишень первым, вторым и третьим стрелками соответственно равны 0,6; 0,5 и 0,4.
Отв.:10/19
13.2.5.19. Ребенок, не умеющий читать, рассыпал разрезанное на буквы слово “каракатица”. Какова вероятность того, что, потеряв одну из гласных букв, неизвестно какую именно, и взяв затем, друг за другом 5 букв он составит слово “карат”?
Отв.:1/1050
13.2.5.20. В урне 3 белых и 2 черных шара. Два игрока поочередно вынимают из урны по шару, не вкладывая их обратно. Выигрывает тот, кто раньше получит белый шар. Найти вероятность того, что выиграет первый игрок.
Отв.:0,7
13.2.5.21. Для передачи сообщения путем подачи сигналов ”точка” и ”тире” используется телеграфная система. Статистические свойства помех таковы, что искажается в среднем 2/5 сообщений ”точка” и 1/5 сообщений ”тире”. Известно, что среди передаваемых сигналов ”точка” и ”тире” встречаются в отношении 5:3. Определить вероятности того, что при приеме сигналов ”точка” и ”тире” в действительности были переданы эти сигналы.
Отв.:5/6;6/11
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
Источник