В сосуде будет состояние вакуума если
Pages: | | 2 | 3 | 4 | 5 | — [ 1 ] — 1. , , : , . ( . vacuum ) . , . . . , . , , , : . , , , . . . , [1] . . , ( ) . , . , . , ( , ) . , , . . , , . , , , ( 1 , 1=133.3223684 =0,001315789474 =1 ..) . , , . , . d, d , , , (10-5 ). 10-9 . , , 10 . , . , , . . , , . . , ( ). , , , . : ; , ; ; , 4,2 .. , : -, . : ; ; ; ; . (. .1): ; ; -. .1. – 2 3. 1*10-1 1*10-2 …, 2 ; 3, . , . ; , . ( ), 3 1. (.2). , , . . (.3) (, ) 1, 3 . . 2. 1*10-2-1*10-1 … ( ) . .2* (.2*). (1) (2). , . . (3) – . : (I) (II). , (4). , , . . , , 106 3 , , – . . , 0,1% . 1892 . . , . . .4 (.301. ) , , . , , . ( ) . .4. : 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 – ; 9 ; 10 . , . ; , , (. . 2.11). ( ). , – . , . . , . : 1) . – , . 2) – , , . 10%. , 106 3 116,6 3. . , . , , . , , . , , , . , : Q=Q+Q, Q ; Q – ( ). Q : Q=5,7((T1/100)4-(T2/100)4)E F2, , (*) T1 T2 () () , ; F2 , 2; E , ( , , , E=1); , =1/(1/e2+F2(1/e1-1)/F1). , , . 1 , 2 , (- , , , ) 1.11. (.187 ) 300 78 4, 0,03 – – 0,03 0,019 0, 0,03 0,018 0, . 0,10 0.06 0,6 – 0,94 – 1) F1 F2. : , .. 2) , , , , . 3) , , . . . ( ..), , . F1 =F2 e1= e2= Ne=Ee/(N+1), N , Ee Ee=/(2-e). .., 2 , .. . (, ), (*). ( : =(14-24), 1 , 2 ) , , , , (.5., . 227, .118). 1, . 3 . , , . . ( , ). (*), , (14-He4)/ (N2 4-He4)=(3004-4,24)/(784-4,24)220 1% . 2-4 . – . , . – 25 (.6., .227 119 ). 2 3. , 4; . . 2,8% . , , – , -. , 340 3 10,7 ( . ). , ( ) 750 , 0,13% . . 5. , . 6. : – 1- 2 ; 2- N2; , 3- ; : 4-; 5 1 ; 2-; 3-; 4- ; 5-; 6- ; 7- : -Bio ” “, 10 . . . () . , . . ( .) , . . , . 2- ( , ). . : ( ), , . ( , ). , , , 10001200 . 11 . . , . , , , . , . , 50 , . . , . 80 , , 110 C (160 ). . 720 . , , ( ), 3000 C. . , , , , . – , , , , , . . , . . ( . %) : 78,08%, 20,95%, 0,93%, ( ) 0,034%, 5105 %; , ( , ) : 1,8103 %, 5,24104 %, 1104 % 8106 %. ; . , , , . , . , % , % , 3/ N2 780 870 78,087 75, O2 209 500 20,95 23, Ar 9 300 0,93 1, 300 0,03 0, CO 18*10-4 12,5*10- Ne 5,24*10-4 0,72*10- He 5, 2,03*10-4 1,28*10- 2, 1,5*10-4 0,8*10- CH4 1, 1,14*10-4 3,3*10- Kr 1, 0,5*10-4 0,035*10- H2 0, 0,5*10-4 0,8*10- N2O 0, 0,08*10-4 0,36*10- Xe 0, 0,01*10-4 0,015*10- O3 0, 6*10-14 6*10-18 7*10- Rn 999 999 99,9999 99, , , , . . , , . , , () , – . 1883 . .. . -, , , , , , -, . , , , . – , . . . (, , ) . – , . . . . . – , . . , () . , . , . . , (). . . , , . . , , . , . , , , . ( ) . , , , . . , , , ( ), ( ). , ( ) . , . , .. , . , , , , , . , , , , . . , . , . . . , , . , ( ). . . . – . : , . , , ( ) . . . 20 , 105 14 . . . . . D2O, . – : 1/6400, . . . ( ), . 3 , . : ( ) , . , , . .., , , , , , . 1.6 ( , , *) 2, N2 . , . , , – . . . – ( ). . : , , , , , . , , , , . . – . . , . . , . , , . , ( . , ), , , . , (). (), , , , , ., . . . N2 , – = SiO2/Al2O3 2, . (, , , , , .; . . : , , , , , , , , ; . . ). – . , , 20-30 0,1-0,6 , – 20-30 . -, 2 (30-95%). , , . , 80% 2, , . 0,3-0,8; 0,2 1,0 */3 . 2 (., , ). 2 , 2 (2,8-10-10 ). N2 . , N2 2 2%, 2 – 40%; 5 -. 4 77%. , , , 0,1-0,6 , 0,5 3,0% 2. , . , 50-60% 2, – 90-95%. 30 3/ 1 . Ne – . , 50% , N2 – 190 200 , . , Ne . , He-Ne , , Ne, 0,1-0,2% . Ne 0,6-0,8. Kr-, , 0,1-0,2% – . , (., 123) 650-750 . 2, r- 500 1000 . , – . Kr- (. ). . . . , , . ; , , . . . – . , , , – ; – , . : () () . , , , – . 2 , () . 2 ; , N2, . 2 N , . , . , , 2: , . , (. . . . ), , . 90-97%- N2 , , , , . , , . : 1) , , , 2) () 3) ( 150) . . () ; . , ., : L =, – , – . , , ( ), . . , 1 99,5%- 2 0,38-0,42 *, LMH = 0,067 *. (, , .), 2 . . . , , , . . , , , . – , , . , , . ( ). ( ) ( ). . , , , . , , . , . . , . , , 100 . 0,6 . , . . , , , 40 (230 ) . , , , . , , , ( ). , , , . , . , , ( ). . (-). , , , , . , , , . , . . , , , , , . . , . , , , . . , , , . 80 (190 C); . 79% 21% , 65% 35% , 87% 13% . , . , . , , . , , ; , , , . , , , , . , . – . , , , . , , . . (, , ) , – . , . . , , . . 17 . 12 ; . 2, , , , , , – , . P, 105 , P, 10 , 647 218 ( 2) 132 38, 405 112,3 126 33, 304 72,7 33 13, 154 49,7 5 2, , . , . . . (), . . , , , , .. 20 (293 ), 0 (-273 ) . , 120 (-153 ), , , , . ( 13- 1971 , 120 ). . – . – , , . , , , , , , , . , , , . . , – , , ( ). , , , , () . – , , (182,97 , 90,19 ). (3 K), . . , , . . , NH4NO3 , 257 . 1759 . .. .. ( 210 ) ( ). ( 200 ) , ( ) . , 196 , , 196 . ., 36 2, ( ), , . -790 , , -1000 . : , , ( ) . , , , () . . , . . . () (). , . , ( ) (. 1.1). () 1792 ( . ). 1823 (. ), 1877 ( . . . ), 1883 (. . . ), 1898 (. ), 1908 (. -). .1. , . . ., . . : 77 63 , 27 24 , 20 14 , 4,2 1 . . . , , . , , , . ( ) . . . . , , , ( , , ), . 1. . . ( ), () ( ), () 182,97 (90,19) 218,75 (54,41) 195,81 (77,35) 210,05 (63,11) 246,09 (27,07) 248,58 (24,58) 252,78 (20,38) 259,19 (13,97) -4 268,93 (4,23) -3 269,93 (3,23) -189,36 (83.8) . ( . .72 ). 1823 .. , , , , ( 110 ). , , , , , , . 1877 . () . () , . , , , . , . 1887 . . . , , , , . 1894 .- () . , . , -, . 1895 . () . () , . . . , . 1898 . , . , 19 . , , . 4 (-4) – 1908 , . , . , 1930 ., , 1934 .. (). 1946 . (). 3, , 1948 – (). , 0,25 . .2. 2. 1780 ., . 1787 .- 1788 . 1823 , , . , 1834 . 1845 , . , , , , , 1845 , . , , , , , . 1861 .. 1862 . 1869 – ., . 1877 : ., . ., . 1883 : 1885 1895 1897 . 1897 . 1895 . 1884 1898 . 1898 . 1902 . 1908 .- . , . , X, s=f(T,X). (1.1) , (1.1), . (1.1) , . . X p, X H, E. , (1.1) . s=const. (1.1) s T (.3.1). , X1. X X1 X4 ( -) s s. , p1 p4, . Q=T*(s-s). (2.1) , ( ), X X1 ( -). s=s, : , X, c , T. , . .. (. Detendre- ) p4 p1. , , X. .3. S-T / , (). , , S T, T S. 2 2 S=S2-S1= dQ / T = dU / T + pdV / T = ..p=const,V=TR/p,dV=(R/p)dT= 1 1 T2 cv dT/T+p ( R / pT )dT =cvln(T2/T1)+Rln(T2/T1)=(cv+R)ln(T2/T1)=cpln(T2/T1). T1 T S2S, T2T. S= S1 + ( dU + pdV ) / T = cpln(T/T1)+ S1. T T=T1e(S-S1)/cp. , S1 , .. , . , . s=f(T,X): X, . , X T, . , , . , 1906 . : , .. T00 s0. . : =00 s0=0. , , . : , . , , , , , . . , T00 . , 0. , , , . T00 T X, . .4.1 – , =0. . .4. . : ( ); (, ) ( ); ( -) ( ); , . , , . – , . : PV= const, P , V , , cp cv, . (r, Ne .) =1,67, (H2, O2, N2 .) =1,4. PV = RT, TV-1= const. 1, , , . , , . , – . , , , , . , . . , . , , . . , ( ). . 1. ( ). . , – PV=RT (1.2) ( , .. ) P1V1 k= P2V2 k= PVk=const (2.2), k , k= Cp/Cv. (1.2) P=RT/V (2.2): T1V1 k-1=T2V2 k-1, .. T2/T1 =(V1/ V2)k- , V=RT/P, : T2/T1 =(P2/ P1) (k-1)/k (3.2) .. k. =Cp/Cv =Cp /(Cp-R), Cp-R=Cv, (k-1)/k=R/ Cp Cp P T, Cp 1,3-1,7 T2/T1 =(P2/ P1)R/Cp (4.2) , Cp-R=Cv, .. Cp =Cv +R, .. . , R. T Q. C=Q/T. , , U . Q=U+ (V=0) 0, Q=U. C=Cv=U/T. =PV, Q=U+=U+ PV, T ( ) Q/T= U/T+ PV /T, C=Cp= Cv+ PV /T (*). , Cp Cv , 10. , Cp Cv , PV=RT, PV RT (*), Cp =Cv +R : T2 =T1(P2/ P1)R/Cp, (5.2) 1 T2 T1. , , . , . , 80 200 1 , k=1,4 84 . , , (. Detendre- ) , . . , .. , ( ..). , , . , . ( ) … , i-i=h h, i i- . i=U+pv. …=h/ h (6.2) 2. (, ) ( ) , , . , , . , . , . , , , . L=vv dv= (v-v). (7.2) (Q=0), , : U-U= (v-v). i=U+pv, i= i-i= v(1-/)- . (8.2) v=RT i=cpT, : T=T-T= T*((k-1)/k))*(1- /). (9.2) T . – ., 36 2, ( ), , . -790 , , -1000 . ( 1. s200.pdf) 3. . , . ( ). ( . drosseln , ) : , . – , , . , . (. 5) , , ( ). 1 2 . . 5. – , V1, V2 . (Q=0), , : = 1V1- 2V2 (10.2) : U = U2 U1 = 1V1- 2V2 (11.2) U1 + 1V1 = U2 + 2V2 (12.2) 1 = 2 (13.2) = U + V . , – . , – PV=RT (14.2), : dU=McvdT (15.2) dH=McpdT (16.2) . , – , . , — : (p + a/V2)(V b)=RT (17.2) , – , . 1. , (b0), (=0). : p(V b)=RT (18.2) pV =RT + p b (19.2) : U = 1V1- 2V2 = R(T1 2) + b(1 2) (20.2) , : U b(1 2) (21.2) 1 2 (21.2) , . , , , – (0 ) 2. (0), (b=0). : (p + a/V2)V=RT (22.2) pV =RT – /V (23.2) : U = 1V1- 2V2 = R(T1 2) + (1/V2 – 1/V1) (24.2) , , : U (1/V2 – 1/V1) (25.2) V2 V1- (25.2) , , . , , , – (0 ). , , – , 1 (2/Rb). – (0) 12/Rb. 12/Rb, (0). ()max =2/Rb (26.2) () ( ). : He 40 K 2 202 Ne 231 K N2 621 K O2 764 K 2 1900 , 2, O2 N2 . He, 2 Ne . , 2.2. 6. . Pages: | | 2 | 3 | 4 | 5 | |
Источник
Молекулы газа, находясь в состоянии хаотического движения, непрерывно сталкиваются друг с другом. Между двумя последовательными столкновениями молекулы проходят некоторый путь l, который называетсядлиной свободного пробега. В общем случае длина пути между последовательными столкновениями различна, но так какмы имеемдело с огромным числом молекул и они находятся в беспорядочном движении, то можно говорить осредней длине свободного пробега молекул <l>.
Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называетсяэффективным диаметром молекулы d (рис. 68). Он зависит от скорости сталкивающихся молекул, т. е. от температуры газа (несколько уменьшается с ростом температуры).
Так как за 1 с молекула проходит в среднем путь, равный средней арифметической скорости <v>, и если <z> – среднее число столкновений, испытываемых одной молекулой газа за 1 с, то средняя длина свободного пробега
Для определения <z> представим себе молекулу в виде шарика диаметром d, которая движется среди других «застывших» молекул. Эта молекула столкнется только с теми молекулами, центры которых находятся на расстояниях, равных или меньших d, т. е. лежат внутри «ломаного» цилиндра радиусом d (рис. 69).
Среднее число столкновений за 1 с равно числу молекул в объеме «ломаного» цилиндра:
где п – концентрация молекул, V = pd2 <v> <v> – средняя скорость молекулы или путь, пройденным ею за 1 с). Таким образом,среднее число столкновений
Расчеты показывают, что при учете движения других молекул
Тогда средняя длина свободного пробега
т. е. <l> обратно пропорциональна концентрации n молекул. С другой стороны, из (42.6) следует, что при постоянной температуре n пропорциональна давлению р. Следовательно,
===================================================
Если из сосуда откачивать газ, то по мере понижения давления число столкновений молекул друг с другом уменьшается, что приводит к увеличению их длины свободного пробега. При достаточно большом разрежении столкновения между молекулами относительно редки, поэтому основную роль играют столкновения молекул со стенками сосуда.Вакуумом называется состояние газа, при котором средняя длина свободного пробега <l> сравнима или больше характерного линейного размера d сосуда, в котором газ находится. В зависимости от соотношения <l> и d различаютнизкий (<l> << d), средний (<l> £ d),высокий (<l> > d) исверхвысокий (<l> >> d) вакуум. Газ в состоянии высокого вакуума называетсяультраразреженным.
Вопросы создания вакуума имеют большое значение в технике, так как, например, во многих современных электронных приборах используются электронные пучки, формирование которых возможно лишь в условиях вакуума. Для получения различных степеней разрежения применяютсявакуумные насосы.В настоящее время применяются вакуумные насосы, позволяющие получить предварительное разрежение (форвакуум) до »0,13 Па, а также вакуумные насосы и лабораторные приспособления, позволяющие получить давление до 13,3 мкПа – 1,33 пПа (10-7 -10-14 мм рт. ст.).
Принцип работы форвакуумного насоса представлен на рис. 72. Внутри цилиндрической полости корпуса вращается эксцентрично насаженный цилиндр. Две лопасти 1 и 1′, вставленные в разрез цилиндра и раздвигаемые пружиной 2, разделяют пространство между цилиндром и стенкой полости на две части. Газ из откачиваемого сосуда поступает в область 3, по мере поворачивания цилиндра лопасть 1 отходит, пространство 3 увеличивается и газ засасывается через трубку 4. При дальнейшем вращении лопасть 1′ отключает пространство 3 от трубки 4 и начинает вытеснять газ через клапан 5 наружу. Весь процесс непрерывно повторяется.
Для получения высокого вакуума применяютсядиффузионные насосы (рабочее вещество – ртуть или масло), которые не способны откачивать газ из сосудов начиная с атмосферного давления, но способны создавать добавочную разность давлений, поэтому их употребляют вместе с форвакуумными насосами. Рассмотрим схему действия диффузионного насоса (рис. 73). В колбе ртуть нагревается, пары ртути, поднимаясь по трубке 1, вырываются из сопла 2 с большой скоростью, увлекая за собой молекулы газа из откачиваемого сосуда (в нем создан предварительный вакуум). Эти пары, попадая затем в «водяную рубашку», конденсируются и стекают обратно в резервуар, а захваченный газ выходит в пространство (через трубку 3), в котором уже создан форвакуум. Если применять многоступенчатые насосы (несколько сопл расположены последовательно), то реально при хороших уплотнениях можно с помощью них получить разрежение до 10-7 мм рт. ст.
Для дальнейшего понижения давления применяются так называемые «ловушки». Между диффузионным насосом и откачиваемым объектом располагают специально изогнутое колено (1 или 2) соединительной трубки (ловушку), которую охлаждают жидким азотом (рис. 74). При такой температуре пары ртути (масла) вымораживаются и давление в откачиваемом сосуде понижается приблизительно на 1-2 порядка. Описанные ловушки называют охлаждаемыми; можно применять также неохлаждаемые ловушки. Специальное рабочее вещество (например, алюмогель) помещают в один из отростков соединительной трубка вблизи откачиваемого объекта, которое поддерживается при температуре 300°С. При достижении высокого вакуума алюмогель охлаждается до комнатной температуры, при которой он начинает поглощать имеющиеся в системе пары. Преимущество этих ловушек состоит в том, что с их помощью в откачиваемых объектах можно поддерживать высокий вакуум уже после непосредственной откачки в течение даже нескольких суток.
Остановимся на некоторых свойствах ультраразреженных газов. Так как в состоянии ультраразрежения молекулы практически друг с другом не сталкиваются, то газ в этом состоянии не обладает внутренним трением. Отсутствие соударений между молекулами разреженного газа отражается также на механизме теплопроводности. Если при обычных давлениях перенос энергии молекулами производится «эстафетой», то при ультраразрежении каждая молекула сама должна перенести энергию от одной стенки сосуда к другой. Явление уменьшения теплопроводности вакуума при понижении давления используется на практике для создания тепловой изоляции. Например, для уменьшения теплообмена между телом и окружающей средой тело помещают в сосуд Дьюара*, имеющий двойные стенки, между которыми находится разреженный воздух, теплопроводность которого очень мала.
* Д. Дьюар (1842-1923) – английскийхимик и физик.
Рассмотрим два сосуда 1 и 2, поддерживаемых соответственно при температурах T1 и Т2 (рис. 75) и соединенных между собой трубкой. Если длина свободного пробега молекул гораздо меньше диаметра соединительной трубки (<l> << d), то стационарное состояние газа характеризуется равенством давлений в обоих сосудах (p1 = р2). Стационарное же состояние ультраразреженного газа (<l> >> d), находящегося в двух сосудах, соединенных трубкой, возможно лишь в том случае, когда встречные потоки частиц, перемещающихся из одного сосуда в другой, одинаковы, т. е.
где п1и п2 – концентрации молекул в обоих сосудах, <v1> и <v2> – средние скорости молекул. Учитывая, что n = p/(kT) и из условия (49.1) получаем
(49.2)
т. е. в условиях высокого вакуума выравнивания давлении не происходит. Если в откачанный стеклянный баллон (рве. 76) на пружину 1 насадить слюдяной листочек 2, одна сторона которого зачернена, и освещать его, то возникнет разность температур между светлой и зачерненной поверхностями листочка. Из выражения (49.2) следует, что в данном случае разным будет и давление, т. е. молекулы от зачерненной поверхности будут отталкиваться с большей силой, чем от светлой, в результате чего листочек отклонится. Это явление называется радиометрическим эффектом. На радиометрическом эффекте основано действие радиометрического манометра.
Источник
ВАКУУМ
Акуум, который удавалось получить при помощи поршневого воздушного насоса, был невысок. Современная техника позволяет получить во много раз большие разрежения.
Как же будут изменяться свойства газов с увеличением разрежения? Начнем постепенно откачивать газ из какого – либо сосуда. Число молекул газа в нем будет постепенно уменьшаться. А раз уменьшится число ударов молекул о стенки, давление газа понизится. Будет уменьшаться и число столкновений молекул между собой, увеличится длина их свободного пробега. Все это будет отражаться на многих свойствах газа.
Величину вакуума обычно характеризуют давлением газа, оставшегося в откачиваемом объеме. Это давление выражают в миллиметрах ртутного столба. В настоящее время вакуумная техника позволяет достигнуть весьма высокой степени разрежения; теперь остаточное давление газа измеряется тысячными и миллионными долями миллиметра ртутного столба. Обозначая величину вакуума, для удобства десятичные дроби заменяют множителем 10 в отрицательной степени, который показывает число знаков после запятой; например 0,001 или 1/1000 обозначается 1 • 10~3; 0,000001-1 • 10~6 и т. д. При уменьшении давления в сотни и тысячи раз по сравнению с обычным давлением воздуха свойства газов не изменяются. Но когда давление газа уменьшается до сотых и тысячных долей миллиметра ртутного столба, в свойствах газов, находящихся в обычных лабораторных приборах или производственных аппаратах, происходят качественные изменения.
Обычное давление от высокого вакуума различают по длине свободного пробега молекул газа. При обычном дав
Лении длина свободного пробега молекул весьма невелика, например для воздуха она составляет около шести сотых микрона. Когда же вакуум достигает 0,01-0,001 (1 • 10 “2- 1 • 10 -3) мм ртутного столба, длина свободного пробега молекул увеличивается и может стать больше размеров сосуда, в котором создается разрежение. При вакууме свыше 1 • 10 ~^мм ртутного столба длина свободного пробега молекул достигает нескольких метров.
При наиболее высоком достигнутом ныне вакууме
1 – 10 “11 мм ртутного столба длина свободного пробега молекул для воздуха (азота и кислорода) приближается к 5000 км. Состояние газа, когда длина свободного пробега молекул превышает размеры сосуда, в котором заключен газ, называется высоким вакуумом. Для обычной аппаратуры и приборов такое состояние достигается при давлении газа ниже 1 • 10 мм ртутного столба, когда длина свободного пробега молекул различных газов измеряется десятками сантиметров. Для наглядности представления о насыщении объема молекулами при различном вакууме приведем следующее сравнение. Увеличим размер одной молекулы до размера песчинки. Тогда одна песчинка при обычном состоянии газа будет приходиться на 40 кубических сантиметров пространства; это значит, что в объеме одного стакана будет находиться всего лишь 5 песчинок. А в высоком вакууме (при остаточном давлении 10~8 мм ртутного столба) одна песчинка будет приходиться в том же масштабе уже на три миллиона кубических метров пространства. В первом случае свободный пробег молекулы будет равен 60 см, а во втором 200 км.
Понятно, что свойства пространства, заполненного молекулами с такой различной плотностью, резко различаются.
Газ, находящийся в состоянии высокого вакуума, обладает необычными свойствами. Его физические свойства зависят от размеров сосуда, в котором он находится.
В состоянии высокого вакуума изменяется прежде всего характер передачи тепла и электричества в газе.
В чем же особенности этого удивительного состояния газа? При высоком вакууме в сообщающихся сосудах, имеющих разную температуру, давление будет не одинаковое. Чтобы доказать это, возьмем два сосуда с воздухом и соединим их трубкой. При обычных условиях давление в них будет одинаковым. Нагреем один из них; движение молекул в нем усилится и давление повысится; через некоторое время
то же произойдет и во втором сосуде. В результате давление в обоих сосудах снова будет одинаковым. А вот в таких же сосудах, где создан «высокий вакуум, при различной температуре давление будет разное. Это объясняется тем, что свойства газа в состоянии высокого вакуума в большой степени определяются состоянием стенок сосуда, в котором газ находится. Молекулы газа, ударяясь о стенки более горячего сосуда, приобретают большую энергию, чем в холодном, и, следовательно, их удары о стенки будут более сильными
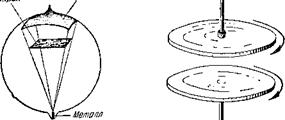
Рис. 9. В высоком вакууме молекулы движутся прямолинейно. |
Рис. 10. Вращение нижнего диска передается верхнему. |

И давление большим. Это давление не будет передаваться в соседний более холодный сосуд, так как число столкновений между молекулами мало и увеличение энергии молекул в другом сосуде будет незначительно.
Если в высоком вакууме между двумя стенками, имеющими различную температуру, поместить пластинку, то пластинка будет испытывать избыточное давление со стороны более нагретой стенки. Молекулы газа, ударившись о поверхность с более высокой температурой, приобретают большую скорость и с большей силой ударяют в пластинку. На этом принципе может быть основано измерение величины вакуума.
Прямолинейность движения молекул в высоком вакууме может быть показана на следующем опыте (рис. 9). Укрепим в стеклянном сосуде металлическую или слюдяную пластинку (экран). В углублении нижней части сосуда поместим небольшое количество легкоплавкого металла, например висмута. Откачаем воздух и запаяем сосуд. После этого нагреем металл. Молекулы металла, испаряясь, летят пря
молинейно и покрывают стенки сосуда тонким слоем. Лишь за пластинкой (экраном) остается «тень», то есть поверхность, не покрытая металлом.
При обычном давлении газы обладают определенной вязкостью, то есть если придать молекулам газа в какой-то части сосуда движение, то оно будет передаваться другим молекулам. Это видно на простом опыте. На рис. 10 показано два диска, способных свободно вращаться вокруг своей оси. Если привести во вращение нижний диск, то его движение передастся прилегающему к диску слою молекул газа и дальше распространится по объему газа и приведет во вращение верхний диск. Происходит это в результате взаимодействия движущихся молекул. В высоком вакууме вращение диска передаваться не будет, так как молекулы движутся, не «задевая» одна другую.
При высоком вакууме изменяется и прохождение электрического тока в газах. Подробнее об электрических явлениях в вакууме мы расскажем ниже.
М Ы познакомились с многочисленными свойствами «пустого» пространства и убедились, что оно далеко не пустое. Однако свойства многих веществ, направление ряда важных технических процессов в большой степени изменяются в разреженном …
И Спользование вакуума в повседневной жизни распространено так широко, что мы этого подчас и не замечаем. Зайдем на колхозную молочную ферму – идет доение коров. К вымени каждой из них …
В Елико давление воздуха на все, находящееся на дне воздушного океана. На каждый квадратный сантиметр поверхности любого тела давит сила, равная примерно 1 кг. С тех пор как была определена …
Источник
