В сосуде находится 1 моль идеального одноатомного газа 100

9081. Цилиндрический сосуд разделен неподвижной теплоизолирующей перегородкой. В одной части сосуда находится кислород, в другой – азот. И концентрация, и давление кислорода в 2 раза больше концентрации и давления азота. Чему равно отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул азота?
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 9081.
9113. Точка (B ) находится в середине отрезка (AC ). Неподвижные точечные заряды (-q ) и (-2q ) ((q ) = 1 нКл) расположены в точках (A ) и (C ) соответственно (см. рисунок). Какой положительный заряд надо поместить в точку (C ) взамен заряда (-2q ), чтобы модуль напряженности электрического поля в точке (B ) увеличился в 2 раза?
Ответ: ________________ нКл.
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 9113.
9145. Точка (B ) находится в середине отрезка (AC ). Неподвижные точечные заряды -(q ) и -(2q ) ((q ) = 2 нКл) расположены в точках (A ) и (C ) соответственно (см. рисунок). Какой положительный заряд надо поместить в точку C вместо заряда -(2q ), чтобы модуль напряженности электрического поля в точке (B ) увеличился в 4 раза?
Ответ: ________________ нКл.
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 9145.
9177. В сосуде находится 1 моль идеального одноатомного газа. В состоянии 1 температура газа равна 100 К. Определите внутреннюю энергию газа в состоянии 2 (см. рисунок).

Ответ: ________________ Дж.
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 9177.
9209. В сосуде находится 1 моль одноатомного идеального газа. В состоянии 2 температура газа равна 600 К. Определите внутреннюю энергию газа в состоянии 1 (см. рисунок).

Ответ: ________________ Дж.
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 9209.
9241. Для охлаждения лимонада массой 200 г в него бросают кубики льда при 0 °С. Масса каждого кубика 8 г. Первоначальная температура лимонада 30 °С. Сколько целых кубиков надо бросить в лимонад, чтобы установилась температура 15 °С? Тепловыми потерями пренебречь. Удельная теплоемкость лимонада такая же, как у воды.
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 9241.
9273. В теплоизолированный сосуд с большим количеством льда при температуре ({t_1}) = 0 °С заливают (m ) = 1 кг воды с температурой ({t_2}) = 44 °С. Какая масса льда ( Delta m ) расплавится при установлении теплового равновесия в сосуде?
Ответ: ________________ кг.
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 9273.
9305. Идеальный газ изобарно нагревают так, что его температура изменяется на ( Delta T ) = 240 К, а объем увеличивается в 1,8 раза. Масса газа постоянна. Найдите конечную температуру газа по шкале Кельвина.
Ответ: ________________ К.
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 9305.
9337. Идеальный газ изохорно нагревают так, что его температура изменяется на ( Delta T ) = 240 К, а давление увеличивается в 1,8 раза. Масса газа постоянна. Найдите начальную температуру газа по шкале Кельвина.
Ответ: ________________ К.
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 9337.
9369. В цепи, изображенной на рисунке, идеальный амперметр показывает 1 А. Найдите напряжение на резисторе ({R_3}).

Ответ: ________________ В.
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 9369.
Для вас приятно генерировать тесты, создавайте их почаще
Источник
Задача по физике – 3104
Теплоизолированный сосуд разделен на две части не проводящим тепло поршнем, который может перемещаться в сосуде без трения. В левой части сосуда находится 1 моль идеального одноатомного газа, в правой – вакуум. Поршень соединен с правой стенкой сосуда пружинкой, длина которой в свободном состоянии равна длине сосуда. Определить теплоемкость системы. Теплоемкостью сосуда, поршня и пружины можно пренебречь.

Подробнее
Задача по физике – 3105
В длинной гладкой теплоизолированной трубе между двумя поршнями с одинаковой массой $m$ находится 1 моль одноатомного газа при температуре $T_{0}$. В начальный момент скорости поршней направлены в одну сторону и равны $5v$ и $v$. До какой максимальной температуры нагреется газ? Поршни тепло не проводят. Массой газа по сравнению с массой поршней можно пренебречь.

Подробнее
Задача по физике – 3106
В калориметре плавает в воде кусок льда. В калориметр опускают нагреватель постоянной мощности $P = 50 Вт$ и начинают ежеминутно измерять температуру воды. В течение первой и второй минут температура воды не изменяется, к концу третьей минуты – увеличивается на $Delta t_{1} = 2^{ circ} С$, а к концу четвертой еще на $Delta t_{2} = 5^{ circ} С$. Сколько граммов воды и льда было изначально в калориметре? Удельная теплота плавления льда $lambda = 33О Дж/г$, удельная теплоемкость воды $c = 4,2 Дж/(град cdot г)$.
Подробнее
Задача по физике – 3107
В герметически закрытом сосуде в воде плавает кусок льда массой $M = О,1 кг$, в который вмерзла свинцовая дробинка массой $m = 5 г$. Какое количество тепла нужно затратить, чтобы дробинка начала тонуть? Теплота плавления льда $lambda = 3,3 cdot 10^{5} Дж/кг$. Температура воды в сосуде – $0^{ circ} С$; плотность $rho_{л} = 0,9 cdot 10^{3} кг/м^{3}$, плотность свинца $rho_{св} = 11,3 cdot 10^{3} кг/м^{3}$, плотность воды $rho_{в} = 10^{3} кг/м^{3}$.
Подробнее
Задача по физике – 3108
В латунном калориметре массой $m_{1} = 0,1 кг$ находится $m_{2} = 5 г$ льда при температуре $t = – 10^{ circ} С$. В калориметр вливают $m_{3} = 30 г$ расплавленного свинца при температуре плавления. Какая температура $theta$ установится в калориметре? Удельная теплоемкость латуни и льда равны соответственно $c_{1} = 0,38 cdot 10^{3} Дж/кг cdot К$; $c_{2} = 2,1 cdot 10^{3} Дж/кг cdot К$. Удельная теплота плавления льда и свинца равны $lambda_{2} = 3,30 cdot 10^{5} Дж/кг; lambda_{св} = 0,25 cdot 10^{5} Дж/кг$. Температура плавления свинца $T_{пл} = 600 К$. Удельная теплоемкость свинца $c_{св} = 0,13 cdot 10^{3} Дж/кг cdot К$.
Подробнее
Задача по физике – 3109
В комнате объемом $V = 50 м^{3}$ воздух имеет температуру $t = 27^{ circ} С$ и относительную влажность $phi_{1} = 30%$. Сколько времени должен работать увлажнитель воздуха, распыляющий воду с производительностью $alpha = 2 кг/ч$, чтобы относительная влажность в комнате повысилась до $phi_{2} =70%$? Давление насыщенных паров при $t = 27^{ circ} p_{н} = 3565 Па$, молярная масса воды $mu = 18 cdot 10^{-3} кг/моль$.
Подробнее
Задача по физике – 3110
В цилиндре под поршнем находится $m = 10 г$ водяного пара при температуре $t = 100^{ circ} C$ и давлении $p = 4 cdot 10^{4} Па$. Какая масса пара сконденсируется, если объем пара изотермически уменьшить в 5 раз?
Подробнее
Задача по физике – 3111
Чему равен коэффициент поверхностного натяжения воды, если с помощью пипетки, имеющей кончик диаметром $d = 0,4 мм$, можно дозировать воду с точностью до $m = 0,01 г$?
Подробнее
Задача по физике – 3112
Верхний конец вертикально расположенного капилляра длиной $l$ закрыт пробкой. Если нижний конец капилляра привести в соприкосновение с поверхностью воды, то вода поднимется в капилляре на высоту $h$. На какую высоту поднимется вода в капилляре, если открыть пробку? Атмосферное давление равно $p_{0}$, плотность воды – $rho$, ее коэффициент поверхностного натяжения – $delta$.
Подробнее
Задача по физике – 3113
Четыре положительных заряда $q,Q,q,Q$ связаны четырьмя нитями, как показано на рис. Определить углы между нитями.

Подробнее
Задача по физике – 3114
Два одинаковых заряженных шарика, подвешенных на нитях одинаковой длины, опускаются в керосин Какова должна быть плотность шариков, чтобы угол расхождения нитей в воздухе и керосине был одинаков? Диэлектрическая проницаемость керосина $epsilon = 2$, плотность керосина $rho = 800 кг/м^{3}$.
Подробнее
Задача по физике – 3115
Тонкое проволочное кольцо радиусом $R$ несет электрический заряд $q$. В центре кольца расположен одноименный с $q$ заряд $Q$, причем $Q gg q$. Определить силу, растягивающую кольцо.
Подробнее
Задача по физике – 3116
Вокруг неподвижного точечного заряда $q_{0} = + 10^{9} Кл$ равномерно вращается под действием кулоновской силы маленький шарик, заряженный отрицательно. Чему равно отношение его заряда к массе (удельный заряд), если радиус орбиты $R = 2 см$, а угловая скорость вращения $omega = 3 с^{-1}$?
Подробнее
Задача по физике – 3117
На вертикальной пластине больших размеров равномерно распределен электрический заряд с поверхностной плотностью $sigma = 3 cdot 10^{-6} Кл/м^{2}$. На прикрепленной к пластине нити подвешен маленький шарик массой $m = 2 г$, несущий заряд того же знака, что и пластина. Найти его заряд, если нить образует с вертикалью угол $alpha = 45^{ circ}$

Подробнее
Задача по физике – 3118
По кольцу радиусом $R$ равномерно распределен заряд $Q$. Определить напряженность и потенциал в центре кольца, а также в точке, отстоящей на расстоянии $h$ от центра кольца по перпендикуляру к его плоскости.
Подробнее
Источник
30. Молекулярная физика (расчетная задача)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
В вертикальном цилиндре, закрытом лёгким поршнем, находится бензол ((C_6H_6)) при температуре кипения (t =80^circ C). При сообщении бензолу некоторого количества теплоты часть его превращается в пар, который при изобарном расширении совершает работу, поднимая поршень. Удельная теплота парообразования бензола ( L = 396cdot 10^3 )Дж/кг, а его молярная масса (M =78cdot 10^{-3}) – кг/моль. Какая часть подводимого к бензолу количества теплоты идёт на увеличение внутренней энергии системы? Объёмом жидкого бензола и трением между поршнем и цилиндром пренебречь. “Досрочная волна 2020 вариант 1”
По первому закону термодинамики [Q=Delta U+A,quad (1)] (Q) – количество теплоты, полученное системой, (Delta U) – изменение внутренней энергии, (A) – работа газа.
А количество теплоты, полученное системой равно [Q=Lm,quad (2)] где (m) – масса образовавшегося пара.
Так как процесс испарения прошел не до конца, то данный процесс изотермический, а значит работа газа будет совершаться за счет изменения массы пара [A=dfrac{m}{M}RT,quad (3)] где (T) – температура газа в Кельвинах.
Объединим (1), (2) и (3) и найдем отношение (dfrac{Delta U}{Q}) [dfrac{Delta U}{Q}=dfrac{Q-A}{Q}=1-dfrac{dfrac{m}{M}RT}{Lm}=dfrac{RT}{LM}=dfrac{8,31 text{ Дж/(К$cdot$моль)}cdot (273+80)text{ К}}{396cdot 10^3text{ Дж/кг}cdot 78cdot 10^{-3}text{ кг/моль}}approx 90,5 %]
Ответ: 90,5
Цикл тепловой машины, рабочим веществом которой является (nu) молей идеального одноатомного газа, состоит из изотермического расширения, изохорного охлаждения и адиабатического сжатия. Работа, совершённая газом в изотермическом процессе, равна (A), а КПД тепловой машины равен (eta). Максимальная температура в этом цикле равна (T_o). Определите минимальную температуру (T) в этом циклическом процессе.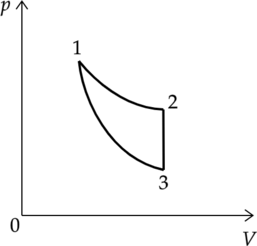
Процессы:
1-2 — изотермический
2-3 — изохорный
3-1 — адиабатический
КПД тепловой машины равен: [; ; ; ; eta = dfrac{A_text{ц}}{Q_text{н}} ; ; ; ; (1)] где (A_text{ц}) — работа, совершенная газом за цикл, (Q_text{н}) — количество теплоты, полученное газом от нагревателя.
Работа газа за цикл есть сумма работ газа в каждом процессе: [A_text{ц} = A_{1-2} + A_{2-3} + A_{3-1}] Так как в процессе 2-3 объем газа постоянен, то его работа равна нулю.
Тогда работа газа за цикл равна: [; ; ; ; A_text{ц} = A_{1-2} + A_{3-1} ; ; ; ; (2)] Далее необходимо найти количество теплоты (Q_text{н}), полученное газом от нагревателя.
Для этого запишем первое начало термодинамики для каждого процесса.
Процесс 1-2: [Q_{1-2} = A_{1-2} + Delta U_{1-2}] Так как процесс 1-2 изотермический, то изменение внутренней энергии газа (Delta U_{1-2}) равно нулю.
Объем газа увеличивается, следовательно, газ совершает положительную работу.
Отсюда получаем, что: [Q_{1-2} = A_{1-2} > 0 ; ; ; Rightarrow ; ; ; ; Q_{1-2} > 0] Процесс 2-3: [Q_{2-3} = A_{2-3} + Delta U_{2-3}] Так как процесс 2-3 изохорный, то работа газа (A_{2-3}) равна нулю.
Давление газа уменьшается, следовательно, его температура также уменьшается (для изохорного процесса (p sim T)).
Следовательно, изменение внутренней энергии газа отрицательно.
Отсюда получаем, что: [Q_{2-3} = Delta U_{2-3} < 0 ; ; ; Rightarrow ; ; ; ; Q_{2-3} < 0] Процесс 3-1:
Так как процесс 3-1 адиабатный, то (Q_{3-1} = 0): [; ; ; ; Q_{3-1} = A_{3-1} + Delta U_{3-1} ; ; ; Rightarrow ; ; ; ; A_{3-1} = – Delta U_{3-1} ; ; ; ; (3)] Таким образом, количество теплоты, полученное газом от нагревателя равно: [Q_text{н} = Q_{1-2}] [; ; ; ; Q_text{н} = A_{1-2} ; ; ; ; (4)] Подставим (2), (4) в (1): [eta = dfrac{A_{1-2} + A_{3-1}}{A_{1-2}}] [; ; ; ; eta = 1 + dfrac{A_{3-1}}{A_{1-2}} ; ; ; ; (5)] Подставим (3) в (5): [; ; ; ; eta = 1 – dfrac{Delta U_{3-1}}{A_{1-2}} ; ; ; ; (6)] Изменение внутренней энергии газа в процессе 3-1 равно: [; ; ; ; Delta U_{2-3} = dfrac{3}{2}nu R(T_1 – T_3) ; ; ; ; (7)] где (R) — универсальная газовая постоянная.
Подставим (7) в (6) и выразим искомую температуру: [eta = 1 – dfrac{dfrac{3}{2}nu R(T_1 – T_3)}{A_{1-2}}] [T_3 = T_1 – dfrac{2}{3nu R} (1 – eta)A_{1-2}] Температура (T_1) является максимальной в этом цикле, так как точка 1 на графике принадлежит изотерме 1-2, которая лежит выше, чем изотерма, проведенная через точку 3: (T_1 = T_o).
Следовательно, температура (T_3) является минимальной: (T_3 = T).
Работа (A_{1-2}) совершена газом в изотермическом процессе: (A_{1-2} = A).
Таким образом, искомая температура равна: [T = T_o – dfrac{2}{3nu R} (1 – eta)A]
Ответ: $T=T_o-dfrac{2}{3nu R}(1-eta)A$
В гладком вертикальном цилиндре под подвижным поршнем массой (M) и площадью (S) находится идеальный одноатомный газ. Поршень в равновесии располагается на высоте (h) над дном цилиндра. После сообщения газу количества теплоты (Q) поршень приподнялся, а газ нагрелся. Найдите, на какой высоте (H) над дном цилиндра находится поршень. Давление в окружающей цилиндр среде равно (p_o).
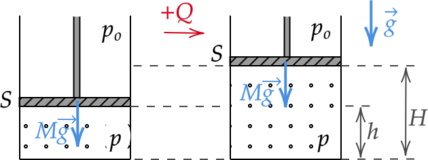
Рассматриваемый процесс — изобарный (так как поршень подвижный и количество вещества газа не изменяется).
Запишем первое начало термодинамики для изобарного процесса: [; ; ; ; Q = A+Delta U ; ; ; ; (1)] где (A) — работа газа, (Delta U) — изменение внутренней энергии газа.
Работа газа и изменение его внутренней энергии равны: [; ; ; ; A = pDelta V ; ; ; ; (2) ; ; ; ; ; ; ; ; ; ; ; Delta U = dfrac{i}{2}nu RDelta T ; ; ; ; (3)] где (p) — давление газа под поршнем, (Delta V) — изменение объема газа, (i) — число степеней свободы (для одноатомного газа (i = 3)), (nu) — количество вещества газа, (R) — универсальная газовая постоянная, (Delta T) — изменение температуры газа.
Подставим (2), (3) в (1): [Q = pDelta V + dfrac{3}{2}nu RDelta T] Для изобарного процесса справедливо равенство: (pDelta V = nu RDelta T).
Тогда уравнение (4) примет вид: [; ; ; ; Q = pDelta V + dfrac{3}{2}pDelta V = dfrac{5}{2}pDelta V ; ; ; ; (5)] Давление внутри сосуда складывается из атмосферного давления и давления, оказываемого поршнем (так как у него есть масса): [; ; ; ; p = p_o + dfrac{Mg}{S} ; ; ; ; (6)] где (g) — ускорение свободного падения.
Изменение объема, занимаемого газом, после сообщения теплоты равно: [; ; ; ; Delta V = (H-h)S ; ; ; ; (7)] Подставим (6), (7) в (5) и выразим высоту, на которой будет находиться поршень над дном цилиндра: [Q = dfrac{5}{2}left( p_o + dfrac{Mg}{S} right) (H-h)S] [H=h+dfrac{2Q}{5(p_oS+Mg)}]
Ответ: $H=h+dfrac{2Q}{5(p_oS+Mg)}$
Два одинаковых теплоизолированных сосуда соединены короткой трубкой с краном. В первом сосуде находится (nu_1) =3 моль гелия при температуре (T_1 = 350) К, во втором (nu_2) = 2 моль аргона при температуре (T_2 = 400) К. Кран открывают. В установившемся равновесном состоянии давление в сосудах становится (p = 6 ) кПа. Определите объём (V ) одного сосуда. Объёмом трубки пренебречь. Ответ дайте в м(^3) и округлите до тысячных.
Так как сосуды теплоизолированные, а газ не совершает работы, то изменение внутренней энергии равно 0, то есть [U_1+U_2=U] где (U_1) – внутренняя энергия первого сосуда, (U_2) – внутренняя энергия второго сосуда, (U) – внутренняя энергия сосудов после открытия краника.
Или [dfrac{3}{2}nu_1R T_1+dfrac{3}{2}nu_2RT_2=dfrac{3}{2}left(nu_1+nu_2right)RT] Отсюда установившаяся температура [T=dfrac{nu_1T_1+nu_2T_2}{nu_1+nu_2}] По закону Клапейрона – Менделеева [p2V=left(nu_1+nu_2right)RT] Отсюда объем одного сосуда [V=dfrac{left( nu_1T_1+nu_2T_2right)R}{2p}=dfrac{left( 3text{ моль} cdot 350text{ К}+2text{ моль} cdot 400text{ К}right)cdot 8,31 text{ Дж/(моль$cdot$ К)}}{2cdot 6cdot 10^3 text{ Па}}approx 1,28text{ м$^3$ }]
Ответ: 1,28
1 моль идеального одноатомного газа сначала изотермически расширили. Затем изохорно нагрели, при этом его давление возросло в 3 раза (см. рисунок). Какое количество теплоты получил газ на участке 2–3, если (T_1=100) К? Ответ дайте в Дж.
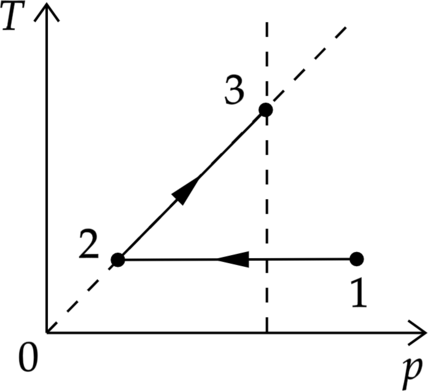
1. Воспользуемся первым законом термодинамики [Q=Delta U+A,] где (Q) – количество теплоты, полученное системой, (Delta U) – изменение внутренней энергии системы, (A) – работа газа.
Так как процесс изохорный, то работа газа равна 0. Распишем изменение внутренней энергии и получим [Q=dfrac{3}{2}nu R Delta T=dfrac{3}{2}nu R left(T_3-T_2right)] 2. Воспользуемся законом Шарля [dfrac{p_2}{T_2}=dfrac{p_3}{T_3} Rightarrow T_3=dfrac{p_3 T_2}{p_2}=3T_2] 3. По условию процесс 1–2 изотермический, значит [T_1=T_2] Следовательно, первый закон термодинамики выглядит [Q=dfrac{3}{2}nu R left(3T_1-T_1right)=3nu R T_1= 3cdot 1 text{ моль} cdot 8,31 text{ Дж/(моль $cdot$ К)}cdot 100text{ К}=2493text{ Дж}]
Ответ: 2493
Один моль одноатомного идеального газа совершает процесс 1–2–3, график которого показан на рисунке в координатах T–V, Известно, что в процессе 1–2 газ совершил работу 3 кДж, а в процессе 2–3 объём газа V увеличился в 2 раза. Какое количество теплоты было сообщено газу в процессе 1–2–3, если его температура Т в состоянии 3 равна 600 К? Ответ дайте в Дж.
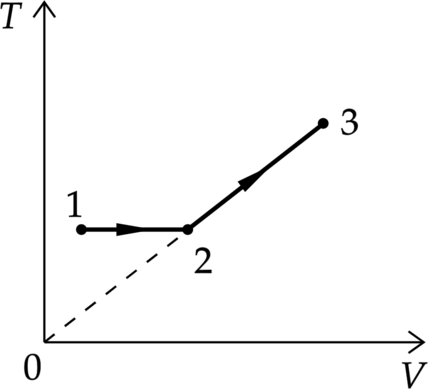
1.Проанализируем процессы
1–2 Процесс изотермический, по закон Бойля-Мариотта [p_1 V_1=p_2V_2] Значит возрастает объем и давление.
2–3 Температура увеличивается линейно объему, следовательно, процесс изобарный.
2. Количество теплоты, полученное в процессе 1–2–3, равно сумме количеств теплоты, полученных в процессах 1–2 и 2–3. [Q_{123}=Q_{12}+Q_{23}] 3. По первому закону термодинамики [Q=Delta U +A,] где (Q) – количество теплоты, полученное системой, (Delta U) – изменение внутренней энергии системы, (A) – работа газа.
Значит в процессе 1–2 изменение внутренней энергии равно 0, а количество теплоты [Q_{12}=A_{12}=3 text{ кДж}] В процессе 2–3 по условию объем возрос в 2 раза, значит по закону Гей-Люссака [dfrac{V_2}{T_2}=dfrac{V_3}{T_3}Rightarrow T_2=dfrac{V_2 T_3}{V_3}= dfrac{600text{ К}}{2}=300text{ К}] По закону Клапейрона–Менделеева [pV=nu R T] Значит количество теплоты, полученное в процессе 2–3 равно [Q_{23}=dfrac{3}{2}nu R left(T_3-T_2right)+pleft( V_3-V_2right)=dfrac{3}{2}nu R left(T_3-T_2right)+nu R left(T_3-T_2right)=dfrac{5}{2}nu R left(T_3-T_2right)] [Q_{23}=dfrac{5}{2}cdot 1 text{ моль} cdot 8,31 text{ Дж/(моль $cdot$ К)}left( 600 text{ К}- 300text{ К}right)= 6232,5 text{ Дж}] А общее количество теплоты [Q=Q_{12}+Q_{23}=6232,5 text{ Дж}+ 3000text{ Дж}=9232,5 text{ Дж}]
Ответ: 9232,5
На рисунке показан циклический процесс постоянное количество одноатомного газа. Работу, которую совершают внешние силы при переходе газа из состояния 2 в состояние 3, равна 5 кДж. Какое количество теплоты газ отдаёт за цикл холодильнику? Ответ дайте в кДж 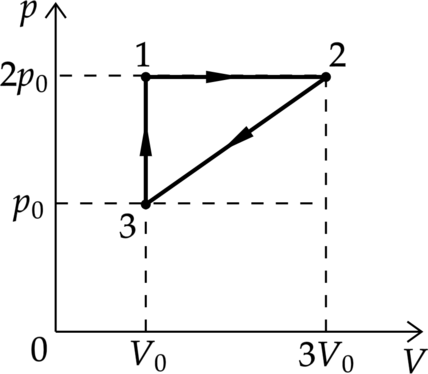
Работа внешних сил в процессе 2–3 равна площади под графиком. [A_{23}=dfrac{p_0+2p_0}{2}left(3V_0-V_0right)=3p_0V_0] (p) – давление, (V) – объем газа, (nu) – количество вещества, (T) – температура газа в Кельвинах.
Воспользуемся первым законом термодинамики [|Q_{text{ хол}}|=|Q_{23}|=Delta U_{23}+A_{32}=dfrac{3}{2}left( nu R T_2 -nu R T_3right)+ 3p_0V_0quad (1)] Также по уравнению Клапейрона – Менделеева [p_2V_2=nu R T_2= 2p_0 cdot 3V_0 =6p_0V_0 quad (2)] [p_2V_2=nu R T_3=p_0V_0 quad (3)] Подставим в (1) формулы (2) и (3) [|Q_{text{ хол}}|=dfrac{3}{2}left(6p_0V_0-p_0V_0right)+3p_0V_0= dfrac{21}{2}p_0V_0=dfrac{7}{2}A_{23}=3,5 cdot 5text{ кДж} =17,5text{ кДж}]
Ответ: 17,5
Источник
