В сосуде находится 11 шаров из которых 4 цветных и 7 белых шаров
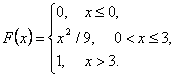
Следствием теорем сложения и умножения является формула полной вероятности.
Допустим, что предполагается провести опыт, об условиях которого можно сделать n исключающих друг друга предположений (гипотез) ,, причем .
Вероятность некоторого события A, которое может появиться только вместе с одной из гипотез, вычисляется по формуле
.
Эта формула носит название формулы полной вероятности..
Получить решение
Если же событие A совершилось и необходимо найти вероятность того, что оно произошло совместно с некоторой гипотезой , то необходимо воспользоваться формулой Бейеса
.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПРИМЕР 13.2.30. Имеются три одинаковые на вид урны; в первой 2 белых и 3 черных шара, во второй – 4 белых и 1 черный шар, в третьей – 3 белых шара. Наугад выбирается одна из урн и из нее вынимается один шар. Найти вероятность того, что этот шар будет белым.
Решение. Опыт предполагает 3 гипотезы:
выбор первой урны; ;
выбор второй урны; ;
выбор третьей урны; .
Рассмотрим интересующее нас событие.
A — вынутый шар белый. Данное событие может произойти только с одной из гипотез .
Тогда .
ПРИМЕР 13.2.31. Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60% деталей отличного качества, а второй – 84%. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь произведена первым автоматом.
Решение. Можно сделать два предположения (гипотезы):
деталь произведена первым автоматом, причем (поскольку первый автомат производит вдвое больше деталей, чем второй) ;
деталь произведена вторым автоматом, причем .
Условная вероятность того, что деталь будет отличного качества, если она произведена первым автоматом , если произведена вторым автоматом .
Вероятность того, что наудачу взятая деталь окажется отличного качества, по формуле полной вероятности равна
.
Искомая вероятность того, что взятая отличная деталь произведена первым автоматом, по формуле Бейеса равна
.
ПРИМЕР 13.2.32. Два стрелка независимо друг от друга стреляют по одной и той же мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,8, для второго – 0,4. После стрельбы в мишени обнаружена одна пробоина. Найти вероятность того, что эта пробоина принадлежит первому стрелку (исход «обе пробоины совпали» отбрасываем, как ничтожно маловероятный).
Решение. До опыта возможны следующие гипотезы:
ни первый, ни второй стрелки не попадут;
оба стрелка попадут;
первый стрелок попадет, а второй – нет;
первый стрелок не попадет, а второй попадает.
Доопытные (априорные) вероятности гипотез:
,
,
,
.
Условные вероятности осуществленного события A — в мишени одна пробоина, при этих гипотезах равны:
.
После опыта гипотезы и становятся невозможными, а послеопытные (апостериорные) вероятности гипотез и по формуле Бейеса будут
; .
Примеры и задачи для самостоятельного решения
Решить задачи, используя формулу полной вероятности и формулу Бейеса
13.2.5.1. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника – 0,9, для велосипедиста – 0,8 и для бегуна – 0,75. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит норму.
Отв.:0,86
13.2.5.2. Из урны, содержащей 5 белых и 3 черных шара, извлекается наудачу один шар и перекладывается в другую урну, которая до этого содержала 2 белых и 7 черных шаров. Цвет перекладываемого шара не фиксируется. Из второй урны наудачу извлекается один шар. Какова вероятность, что этот шар окажется белым?
Отв.:21/80
13.2.5.3. В урну, содержащую шаров, опущен белый шар, после чего наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров (по цвету).
Отв.:(n+2)/(2(n+1))
13.2.5.4. В условиях предыдущей задачи из урны был извлечен белый шар. Найти вероятность того, что в урне было белых шаров.
Отв.:2(m+1)/((n+1)(n+2))
13.2.5.5. В пирамиде 5 винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом равна 0,95; для винтовки с обычным прицелом эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки.
Отв.:0,85
13.2.5.6. В условиях предыдущей задачи стрелок попал в мишень. Определить вероятность того, что он стрелял а) из винтовки с оптическим прицелом; б) из винтовки с обычным прицелом.
Отв.:а)57/85; б)28/85
13.2.5.7. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы курса 4, из второй – 6, из третьей группы – 5 студентов. Вероятности того, что студент первой, второй и третьей группы попадает в сборную института, соответственно равны 0,9; 0,7 и 0,8. Наудачу выбранный студент в итоге соревнования попал в сборную. К какой из групп вероятнее всего принадлежал этот студент?
Отв.:18/59;21/59;20/59
13.2.5.8. Из полного набора 28 костей домино наудачу извлечена кость. Найти вероятность того, что вторую извлеченную наудачу кость можно приставить к первой.
Отв.:7/18
13.2.5.9. В первой урне содержится 10 шаров, из них 8 белых; во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух шаров наудачу взят один шар. Найти вероятность того, что взят белый шар.
Отв.:0,5
13.2.5.10. Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин, проезжающих по тому же шоссе как 3:2. Вероятность того, что будет заправляться грузовая машина равна 0,1; для легковой машины эта вероятность равна 0,2. Найти вероятность того, что наудачу выбранная машина потребует заправки.
Отв.:
13.2.5.11. В условиях предыдущей задачи к бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.
Отв.:3/7
13.2.5.12. В группе из 10 студентов, пришедших на экзамен, 3 подготовлены на отлично, 4 – хорошо, 2 – посредственно, 1 – плохо. В экзаменационных билетах имеется 20 вопросов. Отлично подготовленный студент знает все 20 вопросов, хорошо подготовленный – 16 вопросов, посредственно подготовленный – 10 вопросов и двоечник – 5 вопросов. Вызванный наугад студент ответил на три произвольно заданных вопроса. Найти вероятность того, что этот студент подготовлен а) отлично; б) плохо.
Отв.:а)114/197; б)1/591
13.2.5.13. При отклонении от нормального режима работы автомата срабатывает сигнализатор С-1 с вероятностью 0,8, а сигнализатор С-11 срабатывает с вероятностью 1. Вероятности того, что автомат снабжен сигнализатором С-1 или С-11 соответственно равны 0,6 и 0,4. Получен сигнал о разделке автомата. Что вероятнее: автомат снабжен сигнализатором С-1 или С-11?
Отв.:P(С-1)= 6/11, Р(С-11)= 5/11
13.2.5.14. В каждой из трех урн содержится 6 черных и 4 белых шара. Из первой урны наудачу извлечен один шар и переложен во вторую урну, после чего из второй урны наудачу извлечен один шар и переложен в третью урну. Найти вероятность того, что шар, наудачу извлеченный из третьей урны, окажется белым.
Отв.:0,4
13.2.5.15. Имеется урн, в каждой из которых белых и черных шаров. Из первой урны во вторую перекладывается наудачу один шар, затем из второй в третью и так далее. Затем из последней урны извлекается один шар. Найти вероятность того, что он белый.
Отв.:a/(a+b)
13.2.5.16. По объекту производится три одиночных независимых выстрела. Вероятность попадания при первом выстреле равна 0,4; при втором – 0,5; при третьем – 0,7. Для вывода объекта из строя заведомо достаточно трех попаданий, при двух попаданиях он выходит из строя с вероятностью 0,6; при одном – с вероятностью 0,2. Найти вероятность того, что в результате трех выстрелов объект будет выведен из строя.
Отв.:0,458
13.2.5.17. Имеются три партии деталей по 20 деталей в каждой. Число стандартных деталей в первой, второй и третьей партиях соответственно равно 20, 15, 10. Из наудачу выбранной партии наудачу извлечена деталь, оказавшаяся стандартной. Деталь возвращают в партию и вторично из той же партии наудачу извлекают деталь, которая также оказывается стандартной. Найти вероятность того, что детали были извлечены из третьей партии.
Отв.:4/29
13.2.5.18. Три стрелка произвели залп, причем две пули поразили мишень. Найти вероятность того, что третий стрелок поразил мишень, если вероятности попадания в мишень первым, вторым и третьим стрелками соответственно равны 0,6; 0,5 и 0,4.
Отв.:10/19
13.2.5.19. Ребенок, не умеющий читать, рассыпал разрезанное на буквы слово “каракатица”. Какова вероятность того, что, потеряв одну из гласных букв, неизвестно какую именно, и взяв затем, друг за другом 5 букв он составит слово “карат”?
Отв.:1/1050
13.2.5.20. В урне 3 белых и 2 черных шара. Два игрока поочередно вынимают из урны по шару, не вкладывая их обратно. Выигрывает тот, кто раньше получит белый шар. Найти вероятность того, что выиграет первый игрок.
Отв.:0,7
13.2.5.21. Для передачи сообщения путем подачи сигналов ”точка” и ”тире” используется телеграфная система. Статистические свойства помех таковы, что искажается в среднем 2/5 сообщений ”точка” и 1/5 сообщений ”тире”. Известно, что среди передаваемых сигналов ”точка” и ”тире” встречаются в отношении 5:3. Определить вероятности того, что при приеме сигналов ”точка” и ”тире” в действительности были переданы эти сигналы.
Отв.:5/6;6/11
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
Источник
Из
60 вопросов, входящих в экзаменационные
билеты, студент подготовил 50. Какова
вероятность того, что вытянутый студентом
билет, содержащий два вопроса, будет
состоять из подготовленных им вопросов?
Задание
2
В
сосуде находится 11 шаров, из которых 4
цветных и 7 белых. Найти вероятность
двукратного извлечения из сосуда
цветного шара:
а)
если вынутый шар возвращается обратно
в сосуд;
б)
если вынутый шар в сосуд не возвращается.
Задание
3
Трое
рабочих обрабатывают однотипные детали.
Первый обработал за смену 20 деталей,
второй – 25, третий – 15. Вероятность
брака для первого рабочего равна 0,03,
для второго – 0,02, для третьего – 0,04. Из
общей выработки за смену наудачу взята
и проверена одна деталь, которая оказалась
бракованной. Найти вероятность того,
что она обработана вторым рабочим.
Задание
4
Вероятность
того, что деталь окажется бракованной,
равна p =
0,3. Составить ряд распределения для
случайной величины X,
представляющей собой число бракованных
деталей в выборке объема n =
4. Определить вероятность того, что в
выборке будет:
а)
ровно k =
2 бракованных деталей;
б)
не более k =
2 бракованных деталей;
в)
ни одна деталь не бракованная.
Найти
функцию распределения F(x),
математическое ожидание M(x),
дисперсию D(x).
Задание
5
Случайная
величина X задана
функцией распределения F(x):
Найти:
1)
плотность распределения вероятностей f(x);
2)
математическое ожидание;
3)
построить графики функций f(x), F(x).
Задание
6
Требуется
найти вероятность попадания в заданный
интервал (4, 8) нормально распределенной
случайно величины, если известны ее
математическое ожидание m =
5 и среднее квадратическое отклонение =
3.
Задание
7
Известны x1, x2,
…, xn –
результаты независимых наблюдений над
случайной величиной X.
50 | 52 | 140 | 138 | 165 | 165 | 210 | 165 | 170 | 142 | 150 | 168 |
103 | 63 | 68 | 88 | 85 | 105 | 110 | 112 | 131 | 125 | 126 | 135 |
148 | 92 | 99 | 102 | 110 | 115 | 118 | 125 | 121 | 118 | 130 | 133 |
141 | 182 | 199 | 205 | 127 | 132 | 135 | 98 | 105 | 119 | 115 | 125 |
124 |
1)
Сгруппировать эти данные в интервальную
таблицу, подобрав длину интервала или
воспользовавшись заданной длиной
интервала.
2)
Построить гистограмму и эмпирическую
функцию распределения.
3)
Найти несмещенные оценки для математического
ожидания и дисперсии случайной величины X.
4)
По критерию Пирсона проверить гипотезу
о том, что случайная величина Xимеет
нормальный закон распределения.
5)Найти
интервальные оценки математического
ожидания и среднего квадратического
отклонения случайной величины X с
уровнем доверия 0,99
Вариант №5
Задание
1
Среди
17 студентов группы, из которых 8 девушек,
разыгрывается 7 билетов. Какова вероятность
того, что среди обладателей билетов
окажутся 4 девушки?
Задание
2
От
группы студентов, состоящей из 14 юношей
и 11 девушек, на профсоюзную конференцию
выбирается два человека. Какова
вероятность того, что среди выбранных
будет хотя бы одна девушка?
Задание
3
Радиолампа
может принадлежать к одной из трех
партий с вероятностью P1,P2, P3,
где P1 = P2 =
0,25, P3 =
0,5. Вероятность того, что радиолампа
проработает заданное число часов, равна
соответственно 0,1; 0,2; 0,4. Определить
вероятность того, что радиолампа
проработает заданное число часов.
Задание
4
Вероятность
того, что деталь окажется бракованной,
равна p =
0,3. Составить ряд распределения для
случайной величины X,
представляющей собой число бракованных
деталей в выборке объема n =
5. Определить вероятность того, что в
выборке будет:
а)
ровно k =
4 бракованных деталей;
б)
не более k =
4 бракованных деталей;
в)
ни одна деталь не бракованная.
Найти
функцию распределения F(x),
математическое ожидание M(x),
дисперсию D(x).
Задание
5
Случайная
величина X задана
функцией распределения F(x):
Найти:
1)
плотность распределения вероятностей f(x);
2)
математическое ожидание;
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Вероятностью события А называют отношение m на n и определяется по формуле:
m — числа всех благоприятных комбинаций этому событию исходов эксперимента;
n — общее число всех возможных исходов эксперимента.
Вероятность события А обозначается Р(А).
Основные понятия классической теории вероятности и свойство вероятности рассмотрено здесь.
Рассмотрим примеры, основанные на классическом определение вероятностей.
Пример 1
В урне 10 красных и 8 синих шаров. Наугад вынимают один. Какова вероятность того, что вынут шар красного цвета?
Решение
$p = frac{{10}}{{18}} = frac{5}{9}$
Пример 2
В урне 2 белых и 5 черных шаров. Из урны вынимают один шар и откладывают в сторону. Этот шар оказался белым. После этого из урны берут еще один шар. Найти вероятность того, что этот шар тоже будет белым.
Решение
$p = frac{{2 — 1}}{{2 + 5 — 1}} = frac{1}{6}$
Пример 3
Игральная кость бросается один раз. Найти вероятность следующих событий:
А1 — появление нечетного числа очков;
A2 — появление не менее 3 очков;
A3 — появление не более 5 очков.
Решение
- Возможные варианты выпадения очков при одном бросании кости: 1, 2, 3, 4, 5, 6. Нечётные — 1, 3, 5. Тогда вероятность равна:
$p({A_1}) = frac{m}{n} = frac{3}{6} = frac{1}{2}$
2. Появление не менее 3 очков — это очки: 3, 4, 5, 6, следовательно
$p({A_2}) = frac{m}{n} = frac{4}{6} = frac{2}{3}$
3. Появление не более 5 очков — это очки: 1, 2, 3, 4, 5, тогда имеем
$p({A_3}) = frac{m}{n} = frac{5}{6} $
Пример 4
Монета брошена два раза. Найти вероятность того, что хотя бы один раз появился «герб».
Решение
Найдем все комбинации n подбрасывания монеты два раза, имеем:
«решка» — «герб»
«герб» — «решка»
«решка» — «решка»
«герб» — «герб»
Составим все комбинации события m А — «при бросании монеты два раза хотя бы один раз появился герб»
«решка» — «герб»
«герб» — «решка»
«герб» — «герб»
Тогда
$p({A}) = frac{m}{n} = frac{3}{4} $
Пример 5
Бросаются одновременно две игральные кости. Найти вероятности следующих событий:
- А1 — сумма выпавших очков равна 9;
2. A2 — произведение выпавших очков равно 6;
3. A3 — сумма выпавших очков больше 4.
Решение
Составим всевозможные комбинаций, при которых сумма очков двух игральных костей равна 9
| Первая кость | Вторая кость |
| Три | Шесть |
| Шесть | Три |
| Пять | Четыре |
| Четыре | Пять |
Итак, m=4
Общее количество комбинаций равно
n=6·6=36
$p({A_1}) = frac{m}{n} = frac{4}{36} = frac{1}{9}$
2. Составим таблицу, при котором произведение выпавших очков равно 6;
| Первая кость | Вторая кость |
| Три | Два |
| Два | Три |
| Шесть | Один |
| Один | Шесть |
m=4, n=6·6=36
$p({A_2}) = frac{m}{n} = frac{4}{36} = frac{1}{9}$
3. Чтобы найти сумму выпавших очков больше 4, сначала найдём сумму очков, которая меньше 4, для этого составим таблицу
| Первая кость | Вторая кость |
| Один | Два |
| Два | Один |
| Один | Один |
| Два | Два |
| Один | Три |
| Три | Один |
m=36-6=30, n=6·6=36
Найдем событие A3 — сумма выпавших очков больше 4
$p({A_3}) = frac{m}{n} = frac{30}{36} = frac{15}{18} $
Пример 6
В коробке 6 одинаковых, занумерованных кубиков. Наудачу по одному извлекают все кубики. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке.
Решение
Событие «номера извлеченных кубиков появятся в возрастающем порядке» может произойти в одном случае, то есть m=1.
По формуле комбинаторики перестановка без повторений найдем число комбинаций извлечения шести кубиков
$n = {P_6} = 6! = 1cdot2cdot3cdot4cdot5cdot6 = 720$
Вероятность извлеченных кубиков в возрастающем порядке равна:
$Pleft( A right) = frac{1}{{720}}$
Пример 7
Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры
Решение
А — «абонент набрал нужные три цифры»
m — число благоприятных комбинаций событию А — одно;
n — число комбинаций, которыми можно набрать три цифры и вычисляется по формуле размещение без повторения, тогда
Пример 8
В пачке 20 перфокарт, помеченных номерами 101, 102, … , 120 и произвольно расположенных. Перфораторщица наудачу извлекает две карты. Найти вероятность того, что извлечены перфокарты с номерами 101 и 120.
Решение
Событие А — «перфораторщица наудачу извлекает две карты с номерами 101 и 120».
Общее число комбинаций выбора 2-ух карт из 20 равно:
$C_{20}^2 = frac{{20!}}{{2!cdot18!}} = frac{{19cdot20}}{{1cdot2}} = 190$
Количество благоприятных комбинаций событию А — одно, получаем
$Pleft( A right) = frac{1}{{C_{20}^2}} = frac{1}{{190}}$
Пример 9
В ящике 10 деталей, из которых четыре окрашены. Сборщик наудачу взял три детали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена.
Решение
А — «хотя бы одна из взятых деталей окрашена»
Событие A может произойти в трёх случаях:
«одна деталь окрашена», «две детали окрашены», «три детали окрашены»
Противоположное событие $overline A $ событию A, это «все три детали не окрашены», получаем вероятность
А противоположное событие исходя из условия задачи находится по формуле
Общее число исходов извлечённых из ящика четыре окрашенных деталей из десяти равно
$m = $C_{6}^4$
Число извлечённых из ящика трех деталей из десяти
$m = $C_{10}^4$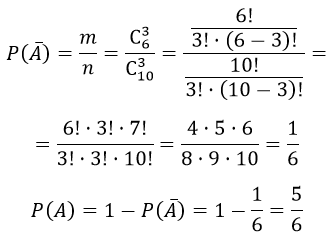
Пример 10
В урне 3 белых и 7 черных. Из урны вынимают сразу два шара. Найти вероятность того, что оба шара будут белыми.
Решение
Пусть событие A — вероятность того, что оба шара будут белыми.
Найдем общее число случаев по формуле сочетание без повторений
Количество благоприятных случаев выбора двух белых шаров из трёх равно
Получаем решение, воспользовавшись общей формулой теории вероятностей
Пример 11
В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.
Решение
А — «три извлеченные детали сборщиком окажутся окрашенными».
Здесь,
m— количество комбинаций извлечения трех окрашенных деталей из десяти;
n— общее число извлечения трех деталей из пятнадцати.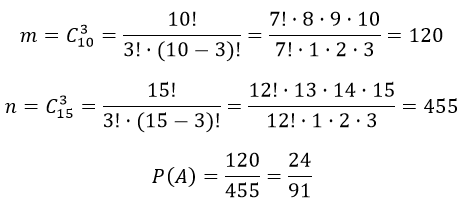
Пример 12
Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором три вопроса.
Решение
А — «студент знает предложенные ему экзаменатором три вопроса»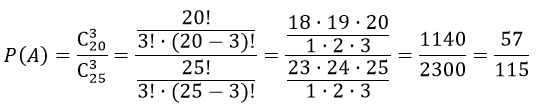
Пример 13
В коробке 5 белых и 7 красных шара. Из нее одновременно наугад вынимают два шара. Найти вероятность того, что они разного цвета.
Решение
$n = C_{7 + 5}^2$
$m = C_5^1 cdot C_7^1$
Через формулу комбинаторики сочетание без повторений, найдём вероятность вынуть шары разных цветов (один красный и один белый шар), равна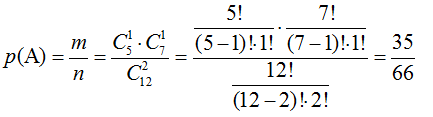
Пример 14
На складе имеется 15 кинескопов, причем 10 из них изготовлены Львовским заводом. Найти вероятность того, что среди пяти взятых наудачу кинескопов окажутся три кинескопа Львовского завода
Решение
А — «из пяти взятых наудачу кинескопов окажутся три кинескопа Львовского завода».
Число способов выбрать три кинескопа Львовского завода из десяти кинескопов Львовского завода равно $C_{10}^3$
Число способов выбрать два кинескопа, которые не изготовлены Львовским заводом из пяти равно $C_{5}^2$
Таким образом
$m = C_{10}^3 cdot C_5^2$
Число комбинаций, которыми можно выбрать пять кинескопов из пятнадцати
$n=C_{15}^5$
Следовательно,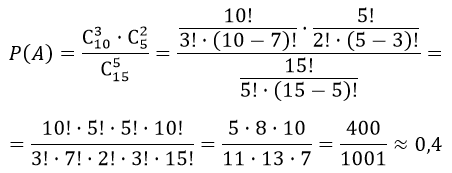
Пример 15
Устройство состоит из пяти элементов, два из которых изношены. При включении устройства включаются случайным образом два элемента. Найти вероятность того, что включенными окажутся неизношенные элементы.
Решение
$Pleft( A right) = frac{{C_3^2}}{{C_5^2}} = frac{3}{{10}} = 0,3$
Пример 16
В коробке пять одинаковых изделий, причем три из них окрашены. Наудачу извлечены два изделия. Найти вероятность того, что среди двух извлеченных изделий окажутся:
1) одно окрашенное изделие;
2) два окрашенных изделия;
3) хотя бы одно окрашенное изделие.
Решение
1) А — «среди двух извлеченных изделий окажется одно окрашенное изделие»
Число способов выбрать одно изделие из трех окрашенных изделий $C_{3}^1$
Неокрашенное изделие можно выбрать $C_{2}^1$
тогда m равно
$m = $C_{3}^1 cdot C_{2}^1$
Общее число способов, которыми можно выбрать два изделия из пяти равно
$n=C_{5}^2$
Имеем,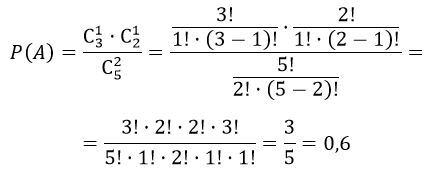
2) В — «два извлеченных изделия окрашены»
Число комбинаций извлечения двух окрашенных изделий $m = $C_{3}^2$
Общее число комбинаций извлечения два изделия из пяти $n=C_{5}^2$
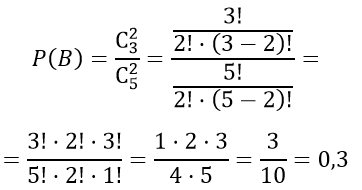
3) С — «извлечено хотя бы одно окрашенное изделие»
Число благоприятных способов извлечения двух изделий нет двух неокрашенных соответствует единице. Тогда: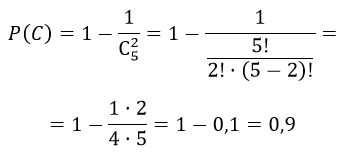
Источник
