В сосуде находится некоторое количество идеального газа 600
8.7. Уравнение Клайперона-Менделеева
8.7.1. Если при сжатии объем идеального газа уменьшился в 2 раза, а давление газа увеличилось в 2 раза, то при этом абсолютная температура газа…
8.7.2. При уменьшении объема идеального газа в 2 раза и увеличении его абсолютной температуры в 4 раза давление газа…
8.7.3. При температуре и давлении один моль идеального газа
занимает объем . Каков объем двух молей газа при том же давлении и температуре ?
8.7.4. Идеальный газ в цилиндре переводится из состояния А в стоянии В так, что его масса при этом не изменяется. Параметры, определяющие состояния газа, приведены в таблице:
|
|
| |
состояние A | 1,0 | 4 | — |
состояние B | 1,5 | 8 | 900 |
Определите число, которое следует ввести в свободную клетку таблицы.
8.7. 5. В сосуде находится некоторое количество идеального газа. Как изменится температура газа, если он перейдет из состояния 1 в состояние 2 (см. рисунок)?
8.7. 6. На рисунке приведены графики двух изотермических процессов, проводимых с одной и той же массой одинакового газа.
Судя по графикам,
1) оба процесса идут при одной и той же температуре
2) в процессе 1 газ начал расширяться позже, чем в процессе 2
3) процесс 1 идет при более высокой температуре
4) процесс 2 идет при более высокой температуре
8.7. 7. В сосуде находится некоторое количество идеального газа. При переходе газа из состояния 1 в состояние 2 (см. рисунок) конечная температура газа
8.7. 8. В сосуде находится некоторое количество идеального газа. При переходе газа из состояния 1 в состояние 2 (см. рисунок) конечная температура газа
8.7. 9. В сосуде находится некоторое количество идеального газа. При переходе газа из состояния 1 в состояние 2 (см. рисунок) конечная температура газа
8.7. 10. В сосуде находится некоторое количество идеального газа. При переходе газа из состояния 1 в состояние 2 (см. рисунок) конечная температура газа
8.7. 11. В сосуде находится некоторое количество идеального газа. При переходе газа из состояния 1 в состояние 2 (см.рисунок) конечная температура газа
8.7. 12. Объем 3 моль водорода в сосуде при температуре 300 К и давлении равен . Чему равен объем 3 моль кислорода при той же температуре и том же давлении?
8.7. 13. В сосуде, закрытом поршнем, находится идеальный газ. На рисунке показан график зависимости объема газа от температуры. В каком состоянии давление газа наибольшее?
8.7. 14. В резервуаре находится 20 кг азота при температуре 300 К и давлении Па. Чему равен объем резервуара? Ответ выразите в кубических метрах и округлите с точностью до десятых.
8.7. 15. В сосуде, закрытом поршнем, находится идеальный газ. Процесс изменения состояния газа показан на диаграмме (см. рисунок). Как менялся объем газа при его переходе из состояния А в состояние В?
8.7. 16. В сосуде находится некоторое количество идеального газа. При переходе газа из состояния 1 в состояние 2 (см.рисунок) конечная температура газа
8.7. 17. В сосуде находится некоторое количество идеального газа. При переходе газа из состояния 1 в состояние 2 (см.рисунок) конечная температура газа
8.7. 18. В сосуде находится некоторое количество идеального газа. При переходе газа из состояния 1 в состояние 2 (см. рисунок) конечная температура газа
8.7. 19. В сосуде находится некоторое количество идеального газа. При переходе газа из состояния 1 в состояние 2 (см.рисунок) конечная температура газа
8.7.20. В баллоне объёмом находится 2 кг молекулярного кислорода при давлении Па. Какова температура кислорода? Ответ выразите в градусах Кельвина и округлите до целых.
8.7.21. Какая масса воздуха выйдет из комнаты, если температура воздуха возросла с до ? Объем комнаты , давление нормальное. Ответ выразите в килограммах и округлите с точностью до десятых.
8.7. 22. В процессе, проводимом с неизменным количеством идеального газа, давление газа изменяется прямо пропорционально квадратному корню из объема газа: . При возрастании давления газа в 2 раза его абсолютная температура .
8.7.23. Идеальный газ расширяется при постоянной температуре. Зависимость объема этого газа от времени показана на рисунке. Какой из приведенных ниже графиков соответствует зависимости давления этого газа от времени?
8.7. 24. Два идеальных газа одинаковой массы занимают одинаковые объёмы при одинаковой температуре. Давление первого газа больше, чем второго. У какого газа меньше масса молекулы?
8.7. 25. На диаграмме зависимости давления р идеального газа неизменной массы от его температуры Т изображены четыре состояния этого газа. Максимальный объём газ занимает в состоянии
8.7. 26. Зависимость объёма идеального газа от температуры показана на VT–диаграмме. В какой из точек давление газа максимально? Масса газа постоянна.
8.7. 27. На рТ–диаграмме изображена зависимость рдавления идеального газа от температуры. Какому состоянию газа из четырёх (А, В, С, D) соответствует наименьший объём? Массу газа считать неизменной.
8.7.28. Зависимость давления идеального газа от температуры представлена на диаграмме р–Т (см. рисунок). В какой из точек объём газа максимален? Масса газа в данном процессе постоянна.
8.7. 29. В сосуде находится идеальный газ. Процесс изобарного изменения состояния газа показан на диаграмме (см. рисунок). Масса газа в процессе изменялась. В какой из точек диаграммы масса газа имеет наибольшее значение?
8.7. 30. На VT–диаграмме изображена зависимость V, объёма идеального газа от температуры (см. рисунок). Какому состоянию газа из четырёх (А, В, С, D) соответствует наименьшее давление? Массу газа считать неизменной.
8.7. 31. В сосуде находится идеальный газ. Процесс изобарного изменения состояния газа показан на диаграмме (см. рисунок). Масса газа в процессе изменялась. В какой из точек диаграммы масса газа имеет наименьшее значение?
8.7. 32. Плотность ≈ 1,2 кг/м3 при нормальном атмосферном давлении и температуре 0 °С имеет…
Источник
За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 72.5%
Ответом к заданию 8 по физике может быть целое число или конечная десятичная дробь.
Задачи для практики
Задача 1
Сосуд вместимостью 12 л, содержащий газ при давлении 0,4 МПа, соединяют с другим сосудом, из которого откачан воздух. Найдите конечное значение давления. Процесс изотермический. Вместимость второго сосуда равна 3,0 л. Ответ выразите в (МПа).
Решение
Дано:
$V_1=12·10^{-3}м^3$
$V_2=3·10^{-3}м^3$
$p_1=0.4·10^6$Па
$T_1=T_2=T=const$
$p_2-?$
Решение:
Из уравнения Менделеева-Клайперона имеем: ${p_1V_1}/{T_1}={p_2(V_2+V_1)}/{T_2}$(1), т.к. $T_1=T_2=T=const$, можно записать: $p_1V_1=p_2(V-2+V_1)$(2), откуда $p_2={p_1V_1}/{(V_2+V_1)}={0.4·10^6·12·10^{-3}}/{15·10^{-3}}=0.32$МПа.
Ответ: 0.32
Показать решение
Полный курс
Задача 2
Газ, занимающий объём 12,32 л, охладили при постоянном давлении на 45 К, после чего его объём стал равен 10,52 л. Какова была первоначальная температура газа? Ответ выразите в (К).
Решение
Дано:
$∆T=45K$
$V_1=12.32·10^{-3}м^3$
$V_2=10.52·10^{-3}м^3$
$p_1=p_2=p=const$
$T_1-?$
Решение:
Из уравнения Менделеева-Клайперона имеем: ${p_1V_1}/{T_1}={p_2V_2}/{T_2}$(1), учитывая, что $p=const$, имеем: ${pV_1}/{T_1}={pV_2}/{T_2}$ или $V_1T_2=V_2T_1$(2). Так как газ охладили, то $T_2=T_1-∆T$(3). Подставим (3) в (2): $V_1T_1-V_1∆T=V_2T_1⇒T_1={V_1∆T}/{(V_1-V_2)}={12.32·10^{-3}·45}/{1.8·10^{-3}}=308K$.
Ответ: 308
Показать решение
Полный курс
Задача 3
В закрытом сосуде находится 120 г газа при комнатной температуре. Какая масса газа вытечет из сосуда, если после открытия крана давление в сосуде понизится в 4 раза? Ответ выразите в (кг).
Решение
Дано:
$T=20+273=293К$
$P_2={P_1}/{4}$
$m_1=0.12$кг
$∆m-?$
$T=const$
$V=const$
Решение:
Зная уравнение Менделеева-Клайперона составим систему 1 и 2.
${tableP_1V={m}/{M}·RT_1; P_2V={m}/{M}·RT_2;$, то $4={m_1}/{m_2}; m_2=0.03$.
$∆m=m_1-m_2=0.12-0.03=0.09$кг.
Ответ: 0.09
Показать решение
Полный курс
Задача 4
В сосуде содержится неон при температуре −3◦С. Во сколько раз увеличится средняя кинетическая энергия теплового движения молекул неона, если его нагреть до 132◦С? В ответе запишите в(во) сколько раз(а).
Решение
Дано:
$t_1=-3+273=270К$
$T_2=132+273=405K$
${E_{к_2}}/{E_{к_1}}$
Решение:
$E_к={3}/{2}KT$.
${E_{к_2}}/{E_{к_1}}={T_2}/{T_1}={405}/{270}=1.5$
Ответ: 1.5
Показать решение
Полный курс
Задача 5
В сосуде содержится аргон при температуре 327◦С. Какая абсолютная температура установится, если концентрацию аргона увеличить в 2 раза, а давление уменьшить в 3 раза? Ответ выразить в (K).
Решение
Дано:
$T^1_{Ар}=327+273=600K$
$n_2=2·n_1$
$P_2={P_1}/{3}$
$T_2$
Решение:
Запишем уравнение состояния газа дважды:
${tableP_1=n_1·K·T_1; P_2=n_2·K·T_2;$ $⇒T_2={T_1}/{2}={600}/{6}=100K$.
Ответ: 100
Показать решение
Полный курс
Задача 6
В сосуде содержится водород, манометр показывает 0,5 атмосферы. Какое установится давление, если концентрацию водорода увеличить в 6 раз, а среднюю кинетическую энергию теплового движения его молекул уменьшить в 4 раза? Ответ выразите в (кПа).
Решение
Дано:
$P_1=0.5·P_{атм}$
$n_2=6·n_1$
$E_{к_2}={E_{к_1}}/{4}$
$P_{атм}=10^5$
Решение:
${tableP_1={2}/{3}·n_1·E_{к_1}; P_2={2}/{3}·n_2·E_{к_2};$ $⇒{0.5·10^5}/{P_2}={1}/{6}:{1}/{4}$.
Для 1 и 2 случая $P_2=75·10^3$Па.
Ответ: 75
Показать решение
Полный курс
Задача 7

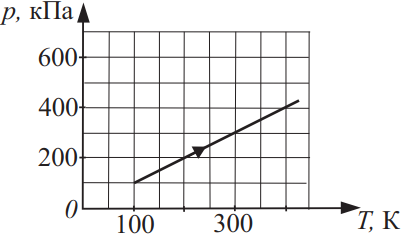
На рисунке показан график изменения давления 10 моль газа при изохорном нагревании. Найдите объём этого газа. Ответ округлите до целого, выразив в (дм3).
Решение
Дано:
$V-?$
$V=const$
$υ=10$моль
Решение:
Из уравнения Менделеева-Клайперона $pV=υRT⇒V={υRT}/{p}={10·8.31·100}/{100·10^3}=83.1дм^3$
Ответ: 83
Показать решение
Полный курс
Задача 8
1 моль идеального газа изохорно охлаждают на 200 К, при этом его давление уменьшается в 3 раза. Найдите первоначальную температуру газа. Ответ выразите в (К).
Решение
Дано:
$υ=1$моль
$υ=const$
$∆T=200K$
${P_1}/{3}=P_2$
$T_0-?$
Решение:
${P_1}/{T_1} > {P_2}/{T_2}$ – изохорный.
$T_0={P_1}/{P_2}·T_2=3(1-200)$
$2T_0=600$
$T_0=300K$
Ответ: 300
Показать решение
Полный курс
Задача 9
Определите плотность азота при температуре 27◦С и давлении 150 кПа. Ответ округлите до десятых. Ответ выразите в (кг/м3).
Решение
Дано:
$T=27°C=300K$
$P=150$кПа
$v=2(Т_2)$
$ρ-?$
Решение:
$PV={m}/{M}·RT$
$ρ·R·T=P·M$
$ρ={P·M}/{R·T}={150·10^3·0.028}/{8.31·300}=1.7{кг}/м^3$.
Ответ: 1.7
Показать решение
Полный курс
Задача 10
Определите температуру азота, имеющего массу 4 г, занимающего объём 831 см3 при давлении 0,2 МПа. Ответ выразите в (К).
Решение
Дано:
$N_2T-?$
$m=4·10^{-3}кг$
$V=831см^3$
$P=0.2·10^6$
$T_?$
Решение:
По закону Менделеева-Клайперона $pV={m}/{M}R·T; T={pv·M}/{m·R}$
$T={0.2·10^6·8.31·0.028}/{4·10^{-3}·8.31}=140K$
Ответ: 140
Показать решение
Полный курс
Задача 11
При повышении температуры идеального газа на 100 К среднеквадратичная скорость движения молекул выросла с 200 м/с до 600 м/с. Насколько надо понизить температуру газа, чтобы среднеквадратичная скорость уменьшилась с 600 м/с до 400 м/с? В ответе запишите на сколько (K).
Решение
Дано:
$∆T=100K↑$
$υ_{cр_1}=200$м/с
$υ_{cр_2}=600$м/с
$∆T-?↓$
$υ_{cр_2}=600$м/с
$υ_{cр_3}=400$м/с
Решение:
В первом процессе $T_1={υ_1^2μ}/{3R}$
$T_2={υ_2^2μ}/{3R}$
$∆T_1=T_2-T_1={μ}/{3R}·(υ_2^2·r_1^2)$
${μ}/{3R}={∆T}/{υ_2^2-r_1^2}={1}/{3200}$
Тогда $∆T_2={μ}/{3R}(υ_2^2-υ_3^2)={1}/{3200}(400^2-600^2)=62.5K$
Ответ: 62.5
Показать решение
Полный курс
Задача 12
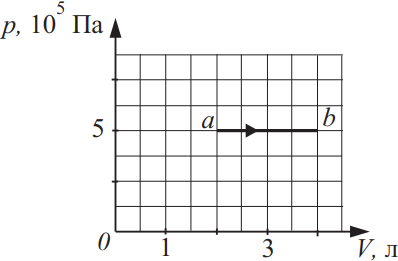
Идеальный газ в количестве 1,5 моль совершает процесс, изображённый на рисунке. Какова температура газа в состоянии b? Ответ выразите в (K), округлив до сотых.
Решение
Дано:
$v=1.5$моль
$T_в-?$
$P=const=10^5$Па
$V_a=2л$
$V_в=4л$
Решение:
По закону Менделеева-Клайперона для точки а и в составим систему: ${tableP·V_a=vRT_a(1); P·V_в=vRT_в(2);$. Из (2) найдем: $T_в={5·10^5·4·10^{-3}}/{1.5·8.31}=160.45K$
Ответ: 160.45
Показать решение
Полный курс
Задача 13
Концентрация молекул идеального одноатомного газа равна 2 · 1024 м−3. Какое давление оказывает газ на стенки сосуда, если при этом средняя кинетическая энергия молекулы равна 1,5 · 10−20 Дж? Ответ выразите в (кПа).
Решение
Дано:
$n=2·10^{24}м^{-3}$
$E_к=1.5·10^{-20}$
$P-?$
Решение:
${tableE_к={3}/{2}KT={3}/{2}K{P}/{nK}; P=nKT;$
Выразим и получим формулу из основ МКТ: $p={E_к·2n}/{3}={1.5·10^{-20}·2·2·10^{24}}/{3}=20$кПа.
Ответ: 20
Показать решение
Полный курс
Задача 14
Температура идеального газа понизилась от 700◦С до 350◦С. Во сколько раз при этом изменилась средняя кинетическая энергия движения молекул газа? Ответ округлить до сотых
Решение
Дано:
$T_1=700°C+273=973K$
$T_2=350°C+273=623K$
${E_1}/{E_2}-?$
Решение:
Из основ молекулярно-кинетической теории известно, что ${E_1}/{E_2}={T_1}/{T_2}$
${E_1}/{E_2}={973}/{623}=1.56$
Ответ: 1.56
Показать решение
Полный курс
Задача 15
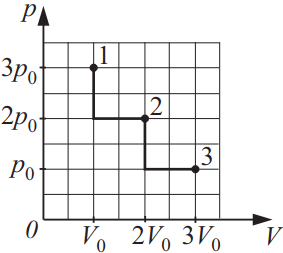
На диаграмме pV изображены процессы перевода некоторой неизменной массы идеального газа из состояния 1 в состояние 3. Начальная (T1) и конечная (T3) температуры связаны между собой соотношением T3/T1…
Решение
Дано:
$Т_1-$начальная
$Т_2$конечная
${T_3}/{T_1}-?$
Решение:
Запишем уравнение Менделеева-Клайперона для начальной и конечной точки состояния: ${table.{p_1·V_1}/{T_1}=υR; .{p_3·V_3}/{T_3}=υR;$.
$⇒{p_1·V_1}/{T_1}={p_3·V_3}/{T_3}⇒{T_3}/{T_1}={p_3·V_3}/{p_1·V_1}⇒{T_3}/{T_1}={p_0·3V_0}/{3p_0·V_0}=1$.
Ответ: 1
Показать решение
Полный курс
Задача 16
При какой температуре молекулы гелия имеют такую же среднюю квадратичную скорость, как молекулы водорода при 27◦С? Ответ выразите в (◦ С).
Решение
Дано:
$t_{H_2}=27°C$
$_{He}=_{H_2}$
$t_{He}-?$
Решение:
Средняя квадратичная скорость молекул гелия и водорода ($He$ и $H_2$) равны соответственно: $_{He}=√{{3RT_{He}}/{μ_{He}}}$, где $T_{He}=t_{He}+273°C$
$_{H_2}=√{{3RT_{H_2}}/{μ_{H_2}}}$, где $T_{H_2}=t_{H_2}-273°C$
Молярные массы гелия $He$ и водорода $H_2$ равны соответственно: $μ_{He}=4·10^{-3}кг/моль; μ_{H_2}=2·10^{-3}кг/моль; T_{H_2}=27°C+273°C=300K$
$√{{3RT_{He}}/{μ_{He}}}=√{{3RT_{H_2}}/{μ_{H_2}}}⇒{3RT_{He}}/{μ_{He}}={3RT_{H_2}}/{μ_{H_2}}⇒T_{He}={T_{H_2}·μ_{He}}/{μ_{H_2}}={300·4·10^{-3}}/{2·10^{-3}}=600K$, тогда $t_{He}=T_{He}-273°C=600°C-273°C=327°C$
Ответ: 327
Показать решение
Полный курс
Задача 17
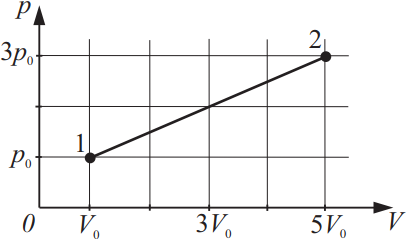
На рисунке изображено изменение состояния идеального газа. Во сколько раз температура в состоянии 2 больше, чем температура в состоянии 1?
Решение
Дано:
$p_1=p_0$
$V_1=V_0$
$p_2=3p_0$
$V_2=5V_0$
${T_2}/{T_1}-?$
Решение:
Из уравнения Менделеева-Клайперона: $pV={m}/{μ}RT$(1), следует равенство ${p_1V_1}/{T_1}={p_2V_2}/{T_2}⇒{p_0V_0}/{T_1}={3p_0·5V_0}/{T_2}$(2).
Из (2) имеем: $p_0V_0T_2=3p_0V_0·5T_1$
$T_2=3·5T_1⇒T_2=15T_1$ или ${T_2}/{T_1}=15$
Ответ: 15
Показать решение
Полный курс
Источник
Тепловое равновесие. Уравнение состояния.
В задании №8 ЕГЭ по физике необходимо решить задачу по теме тепловое равновесие. Кроме этого могут встретиться задания на уравнение состояния идеального газа. Ниже мы приведем краткую теорию, необходимую для решения данных заданий.
Теория к заданию №8 ЕГЭ по физике
Тепловое движение
Формула для средней энергии движения молекул идеального газа справедлива и для реального, который приближен максимально к идеальному: он одноатомный и сильно разреженный. В таком газе молекула может преодолеть расстояние между стенками внутри сосуда, не соударяясь с иными молекулами.
Кинетическая энергия теплового движения молекул газа определяется формулой: где k – постоянная Больцмана, Т — абсолютная температура (т.е. температура в кельвинах) Уравнение Менделеева-Клапейрона имеет вид: pV=vRT. Здесь : p – давление газа,V- его объем. v – скорость его молекул, R – универсальная газовая постоянная, T- температура газа.
Закон Шарля (изохорный процесс)
Изохорным процессом называют изменение состояния газа (динамика его давления и температуры), при постоянном объеме. З-н Шарля.Для неизменной массы газа при постоянном объеме отношение давления газа к его температуре есть величина постоянная: P/T=const. Для двух разных состояний одного и того же газа при постоянном объеме этот закон запишется так: P1 /T1= P2 /T2 Этот закон также можно получить из уравнения Менделеева – Клапейрона: : P/T=vR/V
Разбор задания №8 ЕГЭ по физике
Демонстрационный вариант 2018
При увеличении абсолютной температуры средняя кинетическая энергия хаотического теплового движения молекул разреженного одноатомного газа увеличилась в 2 раза. Начальная температура газа 250 К. Какова конечная температура газа?
Алгоритм решения:
- Записываем формулу, связывающую энергию движения молекул газа с температурой.
- Рассматриваем характер зависимости тепловой энергии от температуры, и как изменения температуры при изменении энергии. Вычисляем искомую температуру.
- Записываем ответ.
Решение:
1. Формула для расчета кинетической энергии теплового движения: Отсюда выражаем температуру Т от энергии: T=2E/(3k) 2. По условию энергия Е возросла в два раза. Поскольку в формуле постоянная Больцмана есть величина постоянная, то температура прямо пропорциональна энергии. Значит, Т возрастет во столько же раз, во сколько увеличится энергия, т.е. в 2 раза. Таким образом, Т = 250 х 2 = 500 К. Ответ: 500
Первый вариант задания (Демидова, №1)
Средняя кинетическая энергия хаотического теплового движения молекул гелия уменьшилась в 4 раза. Определите конечную температуру газа, если его начальная температура равна 900 К.
Алгоритм решения:
- Выписываем формулу, которая связывает кинетическую энергию с температурой.
- Рассматриваем характер зависимости тепловой энергии от температуры и как изменится температура при изменении энергии.
- Записываем ответ.
Решение:
Кинетическая энергия молекул газа определяется формулой: Пусть начальная энергия молекул газа была Е1,а конечная Е2. Начальную температуру этого газа обозначим Т1, а конечную Т2. Используя формулу для кинетической энергии, запишем отношение Е2/Е1, сократив на 3, на 2 и на k: . Получим: Поскольку по условию Е1=4Е2, то . Ответ: 225
Второй вариант задание (Демидова, №22)
Объём 1 моль водорода в сосуде при температуре Т и давлении р равен V1. Объём 2 моль водорода при том же давлении и температуре 3T равен V2. Чему равно отношение V2/V1. (Водород считать идеальным газом.)
Алгоритм решения:
- Анализируем условие задачи и определяем какой закон необходимо использовать в данном случае.
- Записываем уравнение Менделеева-Клапейрона.
- Находим отношение объемов.
- Записываем ответ.
Решение:
1.Уравнение Менделеева-Клапейрона для 1-го объема: pV1=v1 RT1, для второго : pV2=v2 RT2, Где ν1=1, υ2 =2 – объем газа в сосуде для 1-го и 2-го случаев соответственно. По условию Т2=3Т1. 2. Отношение объемов равно: Ответ: 6
Третий вариант задания (Демидова, №28)
На рисунке изображено изменение состояния постоянной массы разреженного аргона. Температура газа в состоянии 2 равна 627 °С. Какая температура соответствует состоянию 1?
Алгоритм решения:
- Анализируем процесс, изображенный на графике. Выражаем из него искомую величину.
- Переводим температуру из градусов Цельсия в градусы Кельвина, определяем значения величин, необходимых для расчета. Вычисляем искомую величину.
- Записываем ответ.
Решение:
Изображенный на графике процесс, происходит при V= const. Следовательно, имеет место изохорный процесс и выполняется закон Шарля , где р1 и Т1 соответствуют состоянию 1, р2 и Т2 – состоянию 2. Отсюда:. Температуре t1=627°С соответствует Т1=627+273=900 К. Из графика видно, что р1=104 Па, р2=3·104 Па. Получаем: Ответ: 300
Даниил Романович | ???? Скачать PDF |
Источник
