В сосуде находиться расплавленный свинец
3 Силы давления жидкости на плоские стенки
3.51 Определить усилие Т, которое нужно приложить к вертикальному тросу для открытия щита, перекрывающего канал прямоугольного сечения. Щит расположен под углом α=60º к горизонту и закреплен шарнирно в точке О (рис. 2.43). Ширина щита в плоскости, перпендикулярной плоскости чертежа, равна В. Глубина воды перед щитом Н1, за щитом Н2. Уровень воды над шарниром h. Принять массу щита M.
Таблица 1 – Исходные данные
| Вариант | Н1, м | Н2, м | h, м | В, м | М, кг |
| а | 2,0 | 0,7 | 0,5 | 3,0 | 400 |
Ответ: Т=77 кН.
3.52 Определить силу давления на затвор, находящийся на глубине Н, м. Указать центр давления.
Таблица 8 – Данные к задаче 5.7
| Номер варианта | Н, м | Ширина затвора, м | Высота затвора, м |
| 5 | 6 | 4 | 1 |
Ответ: Р=254601 Н, hd=6,513 м.
3.53 В воде плавает герметично закрытая бочка (рис. 3.35). Определить результирующую силу давления на дно бочки, если давление в ней рОи=0,1·105 Па, плотность бензина ρб=750 кг/м³, Н=1,2 м, h=0,8 м, D=0,4 м.
Ответ: Р=9260 Н.
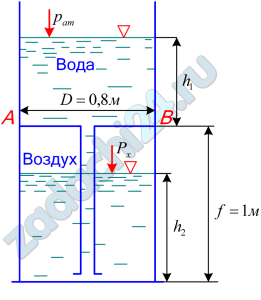
3.54 Вычислить силу суммарного гидростатического давления воды на днище АВ. Предварительно определить толщину h2 слоя воды, которая стечет в нижнюю часть резервуара, учитывая при этом, что сумма глубин наполнения водой, залитой в резервуар, его верхней и нижней частей h1+h2=f.
Процесс сжатия воздуха под днищем AB при стекании воды считать изотермическим.
Ответ: F=4234 H.
3.55 В боковой вертикальной стенке резервуара имеется отверстие, которое перекрывается щитом в форме эллипса размерами а=1,5 м, b=2,5 м (рис. 3.43). Определить силу гидростатического давления воды на щит и положение центра давления, если Н=0,3 м, вакуумметрическое давление в резервуаре р0в=20 кПа.
Ответ: Рх=28,6 кН, hD=1,384 м.
3.56 Прямоугольное отверстие высотой h=0,4 м и шириной b=1,0 м в вертикальной стенке закрытого резервуара с водой закрыто шитом (рис. 3.39). Определить силу и центр давления воды на шит, если Н=0,5 м, избыточное давление в резервуаре р0и=12 кПа.
Ответ: Рх=5977 Н, hD=1,532 м.
3.57 В сосуде находится расплавленный свинец (ρсв=11000 кг/м³). Определить силу давления, действующую на дно сосуда (рис. 3.34), если высота уровня свинца h=500 мм, диаметр сосуда D=400 мм, показание вакуумметра рв=30 кПа.
Ответ: Р=3009 Н.
3.58 Определить точку приложения и силу давления жидкости на плоскую крышку люка в форме полукруга, если относительная плотность жидкости δ=1,25, H=R=1,2 м (рис. 3.33).
Ответ: Р=18,4 кН, hD=1,733 м.
3.59 Затвор квадратного сечения со стороной а может вращаться вокруг горизонтальной оси О, проходящей через центр затвора. Определить силу F, которую нужно приложить к нижней кромке затвора, чтобы его закрыть, если глубина воды перед затвором h. В штольне справа воздух. Трением пренебречь, ρв=1000 кг/м³.
Таблица 3 – Исходные данные
| Вариант | h, м | а, м |
| 12 | 4 | 2,2 |
Ответ: F=13797 Н.
3.60 Поворотный клапан АО закрывает выход из бензохранилища в трубу квадратного сечения со стороной h, м. Прямоугольная пластина клапана опирается на срез трубы, сделанный под углом α=45º. В трубе жидкость отсутствует.
Определить (без учета трения в опоре «О» клапана и в ролике «В») силу Т натяжения троса, необходимую для открытия клапана, если уровень бензина Н, м (см. по варианту), а давление над ним по манометру рм, кг/см². Удельный вес бензина 750 кг/м³.
Источник
Задачи по гидравлике с готовыми решениями
РМ.МАДИ.10
Задачи можно купить или заказать новые обратившись по (skype)
Определить разность уровней пьезометров h.
Система находится в равновесии.
Соотношение площадей поршней равно 3. H = 0,9 м.
Определить разность уровней h в пьезометрах при равновесии поршней мультипликатора, если D/d = 5, H = 3,3 м. Построить график h = f(D/d), если D/d = 1,5 ÷ 5.
Тонкостенный сосуд, состоящий из двух цилиндров диаметрами d = 100 мм и D = 500 мм, нижним открытым концом опущен под уровень воды в резервуаре А и покоится на опорах С, расположенных на высоте b = 0,5 м над этим уровнем.
Определить величину силы, воспринимаемой опорами, если в сосуде создан вакуум, обусловивший поднятия воды в нем на высоту a + b = 0,7 м. Собственная вес сосуда G = 300 Н. Как влияет на результат изменение диаметра d?
Определить абсолютное давление воздуха в сосуде, если показание ртутного прибора h = 368 мм, высота H = 1 м. Плотность ртути ρрт = 13600 кг/м 3 . Атмосферное давление pатм = 736 мм рт. ст.
Определить давление над поршнем p01, если известны: усилия на поршни P1 = 210 Н, P2 = 50 Н; показание прибора p02 = 245,25 кПа; диаметры поршней d1 = 100 мм, d2 = 50 мм и разность высот h = 0,3 м. ρрт/ρ = 13,6.
Определить давление p в гидросистеме и вес груза G, лежащего на поршне 2, если для его подъема к поршню 1 приложена сила F = 1 кН. Диаметры поршней: D = 300 мм, d = 80 мм, h = 1 м, ρ = 810 кг/м 3 . Построить график p = f(D), если D изменяется от 300 до 100 мм.
Определить максимальную высоту Нmax, на которую можно подсасывать бензин поршневым насосом, если давление его насыщенных паров составляет hн.п. = 200 мм рт. ст., а атмосферное давление hа = 700 мм рт. ст. Чему равна при этом сила вдоль штока, если Н = 1 м, ρб = 700 кг/м 3 ; D = 50 мм?
Построить график F = ƒ(D) при изменении D от 50 мм до 150 мм.
Определить диаметр D1 гидравлического цилиндра, необходимый для подъема задвижки при избыточном давлении жидкости p = 1 МПа, если диаметр трубопровода D2 = 1 м и масса подвижных частей устройства m = 204 кг. При расчете коэффициент трения задвижки в направляющих поверхностях принять f = 0,3, силу трения в цилиндре считать равной 5% от веса подвижных частей. Давление за задвижкой равно атмосферному, влиянием площади штока пренебречь.
Построить график зависимости D1 = f(p), если p изменяется в пределах от 0,8 до 5 МПа.
При зарядке гидравлического аккумулятора насос подает воду в цилиндр A, поднимая плунжер B вместе с грузом вверх. При разрядке аккумулятора плунжер, скользя вниз, выдавливает под действием силы тяжести воду из цилиндра в гидравлические прессы.
1. Определить давление воды при зарядке pз (развиваемое насосом) и разрядке pр (получаемое прессами) аккумулятора, если масса плунжера вместе с грузом m = 104 т и диаметр плунжера D = 400 мм.
Плунжер уплотнен манжетой, высота которой b = 40 мм и коэффициент трения о плунжер f = 0,1.
Построить график pз = f(D) и pр = f(D), если D изменяется в пределах от 400 до 100 мм, массу плунжера с грузом считать неизменной.
В герметическом сосуде-питателе А находится расплавленный баббит (ρ = 8000 кг/м 3 ). При показании вакуумметра pвак = 0,07 МПа заполнение разливочного ковша Б прекратилось. При этом H = 750 мм. Определить высоту уровня баббита h в сосуде-питателе А.
Определить силу F, необходимую для удержания поршня на высоте h2 = 2 м над поверхностью воды в колодце. Над поршнем поднимается столб воды высотой h1 = 3 м. Диаметры: поршня D = 100 мм, штока d = 30 мм. Вес поршня и штока не учитывать.
В сосуде находится расплавленный свинец (ρ = 11 г/см 3 ). Определить силу давления, действующую на дно сосуда, если высота уровня свинца h = 500 мм, диаметр сосуда D = 400 мм, показание мановакуумметра pвак = 30 кПа.
Построить график зависимости силы давления от диаметра сосуда, если D изменяется от 400 до 1000 мм
Определить давление p1 жидкости, которую необходимо подвести к гидроцилиндру, чтобы преодолеть усилие, направленное вдоль штока F = 1 кН. Диаметры: цилиндра D = 50 мм, штока d = 25 мм. Давление в бачке p = 50 кПа, высота H = 5 м. Силу трения не учитывать. Плотность жидкости ρ = 10 3 кг/м 3 .
Система в равновесии. D = 100 мм; d = 40 мм; h = 0,5 м.
Какое усилие надо приложить на поршни А и В, если на поршень С действует сила P1 = 0,5 кН? Трением пренебречь. Построить график зависимости P2 от диаметра d, который изменяется от 40 до 90 мм.
Определить силу F на штоке золотника, если показание вакуумметра pвак = 60 кПа, избыточное давление p1 = 1 МПа, высота H = 3 м, диаметры поршней D = 20 мм и d = 15 мм, ρ = 1000 кг/м 3 .
Построить график F = f(D), если D изменяется от 20 до 160 мм.
Задача 1.32
Система из двух поршней, соединенных штоком, находится в равновесии. Определить силу F, сжимающую пружину. Жидкость, находящаяся между поршнями и в бачке, – масло с плотностью ρ = 870 кг/м 3 . Диаметры: D = 80 мм; d = 30 мм; высота Н = 1000 мм; избыточное давление р = 10 кПа.
Задача 1.35
Определить нагрузку P на болты крышек A и Б гидравлического цилиндра диаметром D = 160 мм, если к плунжеру диаметром d = 120 мм приложена сила F = 20 кН.
Построить график зависимости P = f(d), если d изменяется от 120 до 50 мм.
На рисунке представлена конструктивная схема гидрозамка, проходное сечение которого открывается при подаче в полость А управляющего потока жидкости с давлением py. Определить, при каком минимальном значении py толкатель поршня 1 сможет открыть шариковый клапан, если известно: предварительное усилие пружины 2 F= 50 H; D = 25 мм, d = 15 мм, p1 = 0,5 МПа, p2 = 0,2 МПа. Силами трения пренебречь.
Определить манометрическое давление pм, если усилие на поршень P = 100 кгс; h1 = 30 см; h2 = 60 см; диаметры поршней d1 = 100 мм; d2 = 400 мм; d3 = 200 мм; ρм/ρв = 0,9. Определить pм.
Определить минимальное значение силы F, приложенной к штоку, под действием которой начнется движение поршня диаметром D = 80 мм, если сила пружины, прижимающая клапан к седлу, равна F = 100 H, а давление жидкости p2 = 0,2 МПа. Диаметр входного отверстия клапана (седла) d1 = 10 мм. Диаметр штока d2 = 40 мм, давление жидкости в штоковой полости гидроцилиндра p1 = 1,0 МПа.
Определить величину предварительного поджатия пружины дифференциального предохранительного клапана (мм), обеспечивающую начало открытия клапана при pн = 0,8 МПа. Диаметры клапана: D = 24 мм, d = 18 мм; жесткость пружины с = 6 Н/мм. Давление справа от большего и слева от малого поршней – атмосферное.
В гидродомкрате с ручным приводом (рис. 27) на конце рычага 2 приложено усилие N = 150 Н. Диаметры напорного 1 и подъемного 4 плунжеров соответственно равны: d = 10 мм и D = 110 мм. Малое плечо рычага с = 25 мм.
С учетом общего к. п. д. гидродомкрата η = 0,82 определить длину l рычага 2, достаточную для подъема груза 3 весом 225 кН.
Построить график зависимости l = f(d), если d изменяется от 10 до 50 мм.
Задача 1.45
Определить высоту h столба воды в пьезометрической трубке. Столб воды уравновешивает полный поршень с D = 0,6 м и d = 0,2 м, имеющий высоту H = 0,2 м. Собственным весом поршня и трением в уплотнении пренебречь.
Построить график h = f(D), если диаметр D изменяется от 0,6 до 1 м.
Задача 1.51
Определить диаметр поршня D, если нагрузка на поршень P = 80,0 кг; глубины воды в цилиндрах H = 20 см, h = 10 см.
Построить зависимость P = f(D), если P = (20…80) кг.
Определить показание двухжидкостного манометра h2, если давление на свободной поверхности в баке p абс = 147,15 кПа, глубина воды в баке H = 1,5 м, расстояние до ртути h1 = 0,5 м, ρрт/ρв = 13,6.
Воздух засасывается двигателем из атмосферы, проходит через воздухоочиститель и затем по трубе диаметром d1 = 50 мм подается к карбюратору. Плотность воздуха ρ = 1,28 кг/м 3 . Определить разрежение в горловине диффузора диаметром d2 = 25 мм (сечение 2-2) при расходе воздуха Q = 0,05 м 3 /с. Принять следующие коэффициенты сопротивления: воздухоочистителя ζ1 = 5; колена ζ2 = 1; воздушной заслонки ζ3 = 0,5 (отнесены к скорости в трубе); сопла ζ4 = 0,05 (отнесен к скорости в горловине диффузора).
Для взвешивания тяжелых грузов 3 массой от 20 до 60 т применяют гидродинамометр (рис. 7). Поршень 1 диаметром D = 300 мм, шток 2 диаметром d = 50 мм.
Пренебрегая весом поршня и штока, построить график показаний давления р манометром 4 в зависимости от массы m груза 3.
На рис. 12 показана схема гидроклапана с золотником диаметром d = 20 мм.
Пренебрегая трением в гидроклапане и весом золотника 1, определить минимальное усилие, которое должна развивать сжатая пружина 2 для уравновешивания в нижней полости А давления масла р = 10 МПа.
Построить график зависимости усилия пружины от диаметра d, если d изменяется в пределах от 20 до 40 мм.
На рис. 14 показана схема гидрораспределителя с плоским клапаном 2 диаметром d = 20 мм. В напорной полости В гидрораспределителя действует давление масла p = 5 МПа.
Пренебрегая противодавлением в полости А гидрораспределителя и усилием слабой пружины 3, определить длину l плеча рычага 1, достаточную, чтобы открыть плоский клапан 2 приложенный к концу рычага силой F = 50 Н, если длина малого плеча a = 20 мм.
Построить график зависимости F = f(l).
На рис. 10 показана схема плунжерного реле давления, в котором при перемещении плунжера 3 влево поднимается штырь 2, переключающий электрические контакты 4. Коэффициент жесткости пружины 1 С = 50,26 кН/м. Реле давления срабатывает, т.е. переключает электрические контакты 4 при осевом прогибе пружины 1, равном 10 мм.
Пренебрегая трением в реле давления, определить диаметр d плунжера, если реле давления должно срабатывать при давлении масла в полости А (при выходе) р = 10 МПа.
Гидравлический мультипликатор (устройство для повышения давления) получает от насоса воду под избыточным давлением p1 = 0,5 МПа. При этом заполненный водой подвижный цилиндр А с внешним диаметром D = 200 мм скользит по неподвижной скалке С, имеющей диаметр d = 50 мм, создавая на выходе из мультипликатор давление p2.
Определить давление p2, принимая силу трения в сальниках равной 10% от силы, развиваемой на цилиндре давлением p1, и пренебрегая давлением в линии обратного хода.
Масса подвижных частей мультипликатора m = 204 кг.
Построить график зависимости p2 = f(D), если D изменяется в пределах от 200 до 500 мм, m, d, p1 считать постоянными.
Задачи можно купить или заказать новые обратившись по (skype)
Источник
Источник
Условие задачи:
В сосуд с водой объемом 0,25 л при 20 °C поместили 50 г расплавленного свинца с температурой 350 °C. Какая температура установится в результате теплообмена в сосуде? Удельные теплоёмкости расплава и твёрдого свинца считать одинаковыми.
Задача №5.2.38 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(V_1=0,25) л, (t_1=20^circ) C, (m_2=50) г, (t_2=350^circ) C, (t-?)
Решение задачи:
Полностью аналогичная задача уже была представлена на сайте, правда в ней расплавленный свинец имел температуру 400 °C. Можете прорешать её после этой, дабы закрепить свои навыки.
В этой задаче нужно обязательно произвести оценку. Давайте для начала определим количество теплоты (Q_1), которое необходимо для нагревания воды массой (m_1) от температуры (t_1) до температуры кипения (t_к) ((t_к=100^circ) C). Это можно сделать по следующей формуле:
[{Q_1} = {c_1}{m_1}left( {{t_к} – {t_1}} right)]
Удельная теплоёмкость воды (c_1) равна 4200 Дж/(кг·°C).
Массу (m_1) представим как произведение плотности воды (rho) (она равна 1000 кг/м3) на объем (V_1), тогда:
[{Q_1} = {c_1}rho {V_1}left( {{t_к} – {t_1}} right)]
Посчитаем численное значение (Q_1) (объем при расчете мы перевели в кубические метры):
[{Q_1} = 4200 cdot 1000 cdot 0,25 cdot {10^{ – 3}} cdot left( {100 – 20} right) = 84000;Дж]
Так как температура расплавленного свинца (t_2) больше температуры его плавления (t_п) ((t_п=327^circ) C), то определим количество теплоты (Q_2), выделяемое при охлаждении расплава свинца от температуры (t_2) до температуры (t_п).
[{Q_2} = {c_2}{m_2}left( {{t_2} – {t_п}} right)]
Удельная теплоёмкость расплава свинца (и твёрдого свинца) (c_2) равна 130 Дж/(кг·°C).
[{Q_2} = 130 cdot 0,05 cdot left( {350 – 327} right) = 149,5;Дж]
Количество теплоты (Q_3), выделяемое при кристаллизации свинца массой (m_2), определим по формуле:
[{Q_3} = lambda {m_2}]
Удельная теплота кристаллизации (плавления) свинца (lambda) равна 25 кДж/кг.
[{Q_3} = 25 cdot {10^3} cdot 0,05 = 1250;Дж]
Количество теплоты (Q_4), выделяемое при охлаждении свинца массой (m_2) от температуры (t_п) до температуры (t_к), равно:
[{Q_4} = {c_2}{m_2}left( {{t_п} – {t_к}} right)]
[{Q_4} = 130 cdot 0,05 cdot left( {327 – 100} right) = 1475,5;Дж]
Видно, что ({Q_1} > {Q_2} + {Q_3} + {Q_4}), значит температура теплового равновесия будет лежать в пределах от (t_1) до (t_к). Запишем уравнение теплового баланса:
[{Q_5} = {Q_2} + {Q_3} + {Q_6}]
Здесь (Q_5) – количество теплоты, необходимое для нагревания воды массой (m_1) от температуры (t_1) до температуры (t); (Q_6) – количество теплоты, выделяемое при охлаждении свинца массой (m_2) от температуры (t_п) до температуры (t). Тогда:
[{c_1}{m_1}left( {t – {t_1}} right) = {c_2}{m_2}left( {{t_2} – {t_п}} right) + lambda {m_2} + {c_2}{m_2}left( {{t_п} – t} right)]
[{c_1}{m_1}left( {t – {t_1}} right) = {c_2}{m_2}left( {{t_2} – t} right) + lambda {m_2}]
Раскроем скобки:
[{c_1}{m_1}t – {c_1}{m_1}{t_1} = {c_2}{m_2}{t_2} – {c_2}{m_2}t + lambda {m_2}]
Все члены с множителем (t) перенесем в левую сторону, вынесем его за скобки, остальные перенесем в правую.
[tleft( {{c_1}{m_1} + {c_2}{m_2}} right) = {c_1}{m_1}{t_1} + {c_2}{m_2}{t_2} + lambda {m_2}]
[t = frac{{{c_1}{m_1}{t_1} + {c_2}{m_2}{t_2} + lambda {m_2}}}{{{c_1}{m_1} + {c_2}{m_2}}}]
Массу (m_1) представим как произведение плотности воды (rho) на объем (V_1), как это уже было сделано выше:
[t = frac{{{c_1}rho {V_1}{t_1} + {c_2}{m_2}{t_2} + lambda {m_2}}}{{{c_1}rho {V_1} + {c_2}{m_2}}}]
Переведём некоторые величины в систему СИ:
[0,25;л = 0,25 cdot {10^{ – 3}};м^3]
[50;г = 0,05;кг]
Численно температура (t) равна:
[t = frac{{4200 cdot 1000 cdot 0,25 cdot {{10}^{ – 3}} cdot 20 + 130 cdot 0,05 cdot 350 + 25 cdot {{10}^3} cdot 0,05}}{{4200 cdot 1000 cdot 0,25 cdot {{10}^{ – 3}} + 130 cdot 0,05}} = 23,2^circ;C = 296,7;К]
Ответ: 296,7 К.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Источник
3.51 Определить усилие Т, которое нужно приложить к вертикальному тросу для открытия щита, перекрывающего канал прямоугольного сечения. Щит расположен под углом α=60º к горизонту и закреплен шарнирно в точке О (рис. 2.43). Ширина щита в плоскости, перпендикулярной плоскости чертежа, равна В. Глубина воды перед щитом Н1, за щитом Н2. Уровень воды над шарниром h. Принять массу щита M.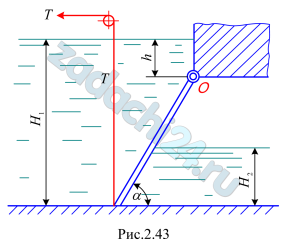
Таблица 1 – Исходные данные
| Вариант | Н1, м | Н2, м | h, м | В, м | М, кг |
| а | 2,0 | 0,7 | 0,5 | 3,0 | 400 |
Ответ: Т=77 кН.
Учебник: Часс С. И. Гидравлика. Гидромеханика. Сборник задач и контрольных заданий. УГГУ Екатеринбург 2009
3.52 Определить силу давления на затвор, находящийся на глубине Н, м. Указать центр давления.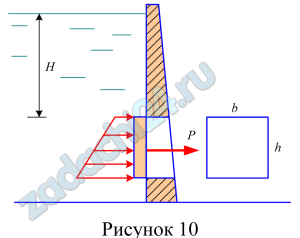
Таблица 8 – Данные к задаче 5.7
| Номер варианта | Н, м | Ширина затвора, м | Высота затвора, м |
| 5 | 6 | 4 | 1 |
Ответ: Р=254601 Н, hd=6,513 м.
3.53 В воде плавает герметично закрытая бочка (рис. 3.35). Определить результирующую силу давления на дно бочки, если давление в ней рОи=0,1·105 Па, плотность бензина ρб=750 кг/м³, Н=1,2 м, h=0,8 м, D=0,4 м.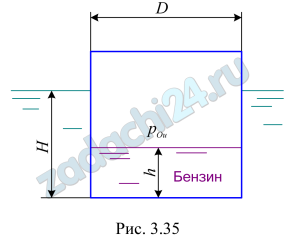
Ответ: Р=9260 Н.
Суров Г.Я Гидравлика в примерах и задачах 2010
3.54 Вычислить силу суммарного гидростатического давления воды на днище АВ. Предварительно определить толщину h2 слоя воды, которая стечет в нижнюю часть резервуара, учитывая при этом, что сумма глубин наполнения водой, залитой в резервуар, его верхней и нижней частей h1+h2=f.
Процесс сжатия воздуха под днищем AB при стекании воды считать изотермическим.
Ответ: F=4234 H.
3.55 В боковой вертикальной стенке резервуара имеется отверстие, которое перекрывается щитом в форме эллипса размерами а=1,5 м, b=2,5 м (рис. 3.43). Определить силу гидростатического давления воды на щит и положение центра давления, если Н=0,3 м, вакуумметрическое давление в резервуаре р0в=20 кПа.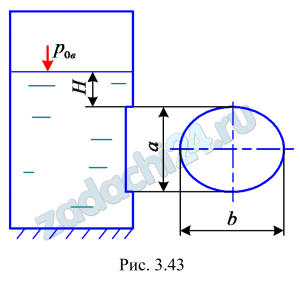
Ответ: Рх=28,6 кН, hD=1,384 м.
Суров Г.Я Гидравлика в примерах и задачах 2010
3.56 Прямоугольное отверстие высотой h=0,4 м и шириной b=1,0 м в вертикальной стенке закрытого резервуара с водой закрыто шитом (рис. 3.39). Определить силу и центр давления воды на шит, если Н=0,5 м, избыточное давление в резервуаре р0и=12 кПа.
Ответ: Рх=5977 Н, hD=1,532 м.
Суров Г.Я Гидравлика в примерах и задачах 2010
3.57 В сосуде находится расплавленный свинец (ρсв=11000 кг/м³). Определить силу давления, действующую на дно сосуда (рис. 3.34), если высота уровня свинца h=500 мм, диаметр сосуда D=400 мм, показание вакуумметра рв=30 кПа.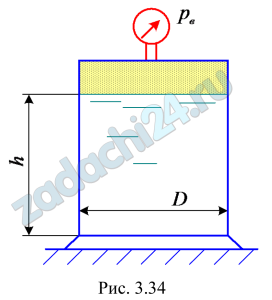
Ответ: Р=3009 Н.
Суров Г.Я Гидравлика в примерах и задачах 2010
3.58 Определить точку приложения и силу давления жидкости на плоскую крышку люка в форме полукруга, если относительная плотность жидкости δ=1,25, H=R=1,2 м (рис. 3.33).
Ответ: Р=18,4 кН, hD=1,733 м.
Суров Г.Я Гидравлика в примерах и задачах 2010
3.59 Затвор квадратного сечения со стороной а может вращаться вокруг горизонтальной оси О, проходящей через центр затвора. Определить силу F, которую нужно приложить к нижней кромке затвора, чтобы его закрыть, если глубина воды перед затвором h. В штольне справа воздух. Трением пренебречь, ρв=1000 кг/м³.
Таблица 3 – Исходные данные
Ответ: F=13797 Н.
3.60 Поворотный клапан АО закрывает выход из бензохранилища в трубу квадратного сечения со стороной h, м. Прямоугольная пластина клапана опирается на срез трубы, сделанный под углом α=45º. В трубе жидкость отсутствует.
Определить (без учета трения в опоре «О» клапана и в ролике «В») силу Т натяжения троса, необходимую для открытия клапана, если уровень бензина Н, м (см. по варианту), а давление над ним по манометру рм, кг/см². Удельный вес бензина 750 кг/м³.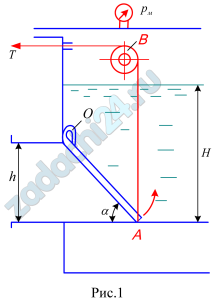
Таблица 1 – Исходные данные
| Вариант | h, м | Н, м | рм, кг/см2 |
| 14 | 0,64 | 2,0 | 0,15 |
Ответ: Т=13,6 кН.
Варианты задачи: 8.
Источник
