В сосуде объемом находится азот при давлении

26.10.2020
0
Главная › Сосуды › В сосуде объемом находится азот при давлении
В сосуде объемом находится азот при давлении thumbnail

Страница 5 из 12

5.81. В сосуде объемом V = 0,1 МПа находится азот при давлении p = 0,1 МПа. Какое количество теплоты Q надо сообщить азоту, чтобы: а) при p = const объем увеличился вдвое; б) при V = const давление увеличилось вдвое?

5.82. В закрытом сосуде находится масса m = 14г азота при давлении pх = 0,1 МПа и температуре t = 27° С. После нагревания давление в сосуде повысилось в 5 раз. До какой температуры t2 был нагрет газ? Найти объем V сосуда и количество теплоты Q, сообщенное газу.

5.83. Какое количество теплоты Qнадо сообщить массе

m = 12г кислорода, чтобы нагреть его на dt= 50° С при p = const ?

5.84. На нагревание массы m = 40 г кислорода от температуры t1 = 16° С до t2 = 40° С затрачено количество теплоты Q = 628Дж. При каких условиях нагревался газ (при постоянном объеме или при постоянном давлении)?

5.85. В закрытом сосуде объемом V = 10 л находится воздух при давлении p = 0,1 МПа. Какое количество теплоты Qнадо сообщить воздуху, чтобы повысить давление в сосуде в 5 раз?

5.86. Какую массу m углекислого газа можно нагреть при p = const от температуры t1 =20° С до t2=100° С количеством теплоты Q = 222Дж? На сколько при этом изменится кинетическая энергия одной молекулы?

5.87. В закрытом сосуде объем V = 2 л находится азот, плотность которого р = 1,4 кг/м3 Какое количество теплоты Q надо сообщить азоту, чтобы нагреть его на dT = 100 К?

5.88. Азот находится в закрытом сосуде объемом V = 3 л при температуре t1=27° С и давлении p1 = 0,ЗМПа. После нагревания давление в сосуде повысилось до p2=2,5МПа. Найти температуру t2азота после нагревания и количество теплоты Q, сообщенное азоту.

5.89. Для нагревания некоторой массы газа на dt1 =50° С при p = const необходимо затратить количество теплоты Q{= 670 Дж.

Если эту же массу газа охладить на dt2 = 100° С при V = const, то выделяется количество теплоты Q2=1005Дж. Какое число степеней свободы i имеют молекулы этого газа?

5.90. Масса m = 10 г азота находится в закрытом сосуде при температуре t1 = 7° С. Какое количество теплоты Qнадо сообщить азоту, чтобы увеличить среднюю квадратичную скорость его молекул вдвое? Во сколько раз при этом изменится температура газа? Во сколько раз при этом изменится давление газа на стенки сосуда?

5.91. Гелий находится в закрытом сосуде объемом V = 2 л при температуре t1 = 20° С и давлении p1= 100 кПа. Какое количество теплоты Q надо сообщить гелию, чтобы повысить его температуру на dt = 100° С? Каковы будут при новой температуре средняя квадратичная скорость его молекул, давление p2, плотность p2гелия и энергия теплового движения W его молекул?

5.92. В закрытом сосуде объемом V = 2 л находится масса m азота и масса m аргона при нормальных условиях. Какое количество теплоты Q надо сообщить, чтобы нагреть газовую смесь на dt = 100°С?

5.93. Найти среднюю арифметическую v, среднюю квадратичную sqr(v2)и наиболее вероятную vв скорости молекул газа, который при давлении p = 40 кПа имеет плотность p = 0,3 кг/м.

5.94. При какой температуре Т средняя квадратичная скорость молекул азота больше их наиболее вероятной скорости на dv = 50 м/с?

5.95. Какая часть молекул кислорода при t = 0° С обладает скоростями v от 100 до 110 м/с?

5.96. Какая часть молекул азота при t = 150° С обладает скоростями v от 300 до 325 м/с?

5.97. Какая часть молекул водорода при t = 0° С обладает скоростями v от 2000 до 2100 м/с?

5.98. Во сколько раз число молекул dN1, скорости которых лежат в интервале от vB до vB + dv , больше числа молекул dN2,

скорости которых лежат в интервале от sqr(v2)до sqr(v2) + dv ?

5.99. Какая часть молекул азота при температуре Т имеет скорости, лежащие в интервале от vB до vB + dv , где dv = 20 м/с.

если: а) Т = 400 К; б) Т = 900 К?

5.100. Какая часть молекул азота при температуре t = 150° С имеет скорости, лежащие в интервале от v1=300m/c до

v2 = 800 м/с?

Источник

Страница 5 из 12

5.81. В сосуде объемом V = 0,1 МПа находится азот при давлении p = 0,1 МПа. Какое количество теплоты Q надо сообщить азоту, чтобы: а) при p = const объем увеличился вдвое; б) при V = const давление увеличилось вдвое?

5.82. В закрытом сосуде находится масса m = 14г азота при давлении pх = 0,1 МПа и температуре t = 27° С. После нагревания давление в сосуде повысилось в 5 раз. До какой температуры t2 был нагрет газ? Найти объем V сосуда и количество теплоты Q, сообщенное газу.

5.83. Какое количество теплоты Qнадо сообщить массе

m = 12г кислорода, чтобы нагреть его на dt= 50° С при p = const ?

5.84. На нагревание массы m = 40 г кислорода от температуры t1 = 16° С до t2 = 40° С затрачено количество теплоты Q = 628Дж. При каких условиях нагревался газ (при постоянном объеме или при постоянном давлении)?

Читайте также:  Характеристика кровеносных сосудов человека

5.85. В закрытом сосуде объемом V = 10 л находится воздух при давлении p = 0,1 МПа. Какое количество теплоты Qнадо сообщить воздуху, чтобы повысить давление в сосуде в 5 раз?

5.86. Какую массу m углекислого газа можно нагреть при p = const от температуры t1 =20° С до t2=100° С количеством теплоты Q = 222Дж? На сколько при этом изменится кинетическая энергия одной молекулы?

5.87. В закрытом сосуде объем V = 2 л находится азот, плотность которого р = 1,4 кг/м3 Какое количество теплоты Q надо сообщить азоту, чтобы нагреть его на dT = 100 К?

5.88. Азот находится в закрытом сосуде объемом V = 3 л при температуре t1=27° С и давлении p1 = 0,ЗМПа. После нагревания давление в сосуде повысилось до p2=2,5МПа. Найти температуру t2азота после нагревания и количество теплоты Q, сообщенное азоту.

5.89. Для нагревания некоторой массы газа на dt1 =50° С при p = const необходимо затратить количество теплоты Q{= 670 Дж.

Если эту же массу газа охладить на dt2 = 100° С при V = const, то выделяется количество теплоты Q2=1005Дж. Какое число степеней свободы i имеют молекулы этого газа?

5.90. Масса m = 10 г азота находится в закрытом сосуде при температуре t1 = 7° С. Какое количество теплоты Qнадо сообщить азоту, чтобы увеличить среднюю квадратичную скорость его молекул вдвое? Во сколько раз при этом изменится температура газа? Во сколько раз при этом изменится давление газа на стенки сосуда?

5.91. Гелий находится в закрытом сосуде объемом V = 2 л при температуре t1 = 20° С и давлении p1= 100 кПа. Какое количество теплоты Q надо сообщить гелию, чтобы повысить его температуру на dt = 100° С? Каковы будут при новой температуре средняя квадратичная скорость его молекул, давление p2, плотность p2гелия и энергия теплового движения W его молекул?

5.92. В закрытом сосуде объемом V = 2 л находится масса m азота и масса m аргона при нормальных условиях. Какое количество теплоты Q надо сообщить, чтобы нагреть газовую смесь на dt = 100°С?

5.93. Найти среднюю арифметическую v, среднюю квадратичную sqr(v2)и наиболее вероятную vв скорости молекул газа, который при давлении p = 40 кПа имеет плотность p = 0,3 кг/м.

5.94. При какой температуре Т средняя квадратичная скорость молекул азота больше их наиболее вероятной скорости на dv = 50 м/с?

5.95. Какая часть молекул кислорода при t = 0° С обладает скоростями v от 100 до 110 м/с?

5.96. Какая часть молекул азота при t = 150° С обладает скоростями v от 300 до 325 м/с?

5.97. Какая часть молекул водорода при t = 0° С обладает скоростями v от 2000 до 2100 м/с?

5.98. Во сколько раз число молекул dN1, скорости которых лежат в интервале от vB до vB + dv , больше числа молекул dN2,

скорости которых лежат в интервале от sqr(v2)до sqr(v2) + dv ?

5.99. Какая часть молекул азота при температуре Т имеет скорости, лежащие в интервале от vB до vB + dv , где dv = 20 м/с.

если: а) Т = 400 К; б) Т = 900 К?

5.100. Какая часть молекул азота при температуре t = 150° С имеет скорости, лежащие в интервале от v1=300m/c до

v2 = 800 м/с?

Источник

Äàëåå: 1.2. 
Çàäà÷è äëÿ ñàìîñòîÿòåëüíîãî
Ââåðõ: 1. 
Ìîëåêóëÿðíàÿ ôèçèêà è
Íàçàä: 1. 
Ìîëåêóëÿðíàÿ ôèçèêà è

1.1.  Ïðèìåðû ðåøåíèÿ
çàäà÷

Ïðèìåð 1.1.  Ñæèæåííûå ãàçû õðàíÿò â ñîñóäàõ,
ñîîáùàþùèõñÿ ñ àòìîñôåðîé. Ìîæíî ëè
äîïóñòèòü èñïàðåíèå æèäêîãî àçîòà îáúåìîì $0,5,{ë}$ è
ïëîòíîñòüþ
$0,81,{ã/ñì}^3$â
çàêðûòîì ñîñóäå îáúåìîì $10,{ë}$ ïðè íàãðåâàíèè
åãî äî òåìïåðàòóðû $20^circ C$, åñëè ñòåíêè ñîñóäà
âûäåðæèâàþò äàâëåíèå
$20,{àòì}$?

hbox to 0.4hsizeÐåøåíèå.
Ïðè ïîâûøåíèè òåìïåðàòóðû æèäêèé àçîò ïåðåéäåò â ãàçîîáðàçíîå
ñîñòîÿíèå.
Ïðèìåì åãî ïðè òåìïåðàòóðå $20^circ C$ çà èäåàëüíûé ãàç è
ïðèìåíèì äëÿ ðåøåíèÿ
óðàâíåíèå Êëàïåéðîíà – Ìåíäåëååâà:

begin{displaymath} PV = {movermu}RT,, end{displaymath}(1)


ãäå $P$, $V$ è $T$ – äàâëåíèå, îáúåì è
òåìïåðàòóðà ãàçà; $m$ – åãî ìàññà, $mu$ – ìàññà
ìîëÿ àçîòà, ðàâíàÿ $28cdot 10^{-3},{êã/ìîëü}$; $R$ – óíèâåðñàëüíàÿ
ãàçîâàÿ ïîñòîÿííàÿ.

Äëÿ îòâåòà íà âîïðîñ çàäà÷è íóæíî îïðåäåëèòü äàâëåíèå ãàçîîáðàçíîãî
àçîòà è ñðàâíèòü åãî ñ
ìàêñèìàëüíî äîïóñòèìûì.

Âûðàçèì èñêîìîå äàâëåíèå èç óðàâíåíèÿ 1:

begin{displaymath} P_x = {mRTovermu V},, end{displaymath}(2)


çäåñü íåèçâåñòíà ìàññà ãàçà, åå ìîæíî îïðåäåëèòü ÷åðåç îáúåì è
ïëîòíîñòü æèäêîãî àçîòà:
$m= rho_1V_1$. Âûðàæåíèå äëÿ èñêîìîãî äàâëåíèÿ â îáùåì âèäå:

begin{displaymath} P_x = {rho_1V_1RTovermu V},. end{displaymath}(3)


Ïðîâåðêà íàèìåíîâàíèÿ åäèíèöû èñêîìîé âåëè÷èíû:

begin{displaymath}[P_x]={{êã}cdot{ì}^3cdot{Äæ}cdot{Ê}cdot{ìîëü}over {ì}^3 ... ...{{Äæ}over{ì}^3}= {{Í}cdot{ì}over{ì}^3}={{Í}over{ì}^2}={Ïà.}end{displaymath}

Ýòî åäèíèöà äàâëåíèÿ â ÑÈ, ñëåäîâàòåëüíî, âûðàæåíèå â îáùåì âèäå
ïîëó÷åíî ïðàâèëüíî.

Âû÷èñëåíèÿ: ïîäñòàâèì ÷èñëà (âñå îíè äîëæíû áûòü âûðàæåíû â
ÑÈ):

begin{displaymath}P_x={8,1cdot 10^2cdot 5cdot 10^{-4}cdot 8,3 cdot 293over 28cdot 10^{-3}cdot 10^{-2}},{Ïà},.end{displaymath}

Ïðåæäå ÷åì âû÷èñëÿòü, ïðîâåäåì äåéñòâèÿ ñî ñòåïåíÿìè:

begin{displaymath}P_x={8,1cdot 5cdot 8,3 cdot 293over 28}cdot 10^{3},{Ïà}=3,52cdot 10^{6},{Ïà},.end{displaymath}

Èñêîìîå äàâëåíèå ðàâíî $3,52cdot 10^6,{Ïà}$ èëè $35,2 {àòì}$ è ïðåâûøàåò
äîïóñòèìîå.

Îòâåò: èñïàðåíèå æèäêîãî àçîòà äàííîé ìàññû â çàêðûòîì ñîñóäå
óêàçàííîãî îáúåìà íåëüçÿ
äîïóñòèòü, òàê êàê ïðè $20^circ C$ äàâëåíèå ïðåâûñèò
äîïóñòèìîå. Ïîýòîìó ñæèæåííûå ãàçû õðàíÿò
â îòêðûòûõ ñîñóäàõ.

Читайте также:  Какое растение чистит кровеносные сосуды

Ïðèìåð 1.2. Öèëèíäðè÷åñêàÿ òðóáêà äëèíîé $ell$ íàïîëîâèíó ïîãðóæåíà â ðòóòü. Çàêðûâ åå ñâåðõó,
òðóáêó âûíèìàþò, ïðè ýòîì ÷àñòü ðòóòè âûëèâàåòñÿ. Êàêîé äëèíû ñòîëáèê
ðòóòè îñòàíåòñÿ â òðóáêå,
åñëè àòìîñôåðíîå äàâëåíèå ðàâíî $H$ ìì ðò. ñò.?

hbox to 0.4hsizeÐåøåíèå.
Ïðèìåì âîçäóõ, íàõîäÿùèéñÿ â òðóáêå íàä ðòóòüþ, çà èäåàëüíûé ãàç.
Ïîñêîëüêó â óñëîâèè çàäà÷è
èçìåíåíèå òåìïåðàòóðû íå îãîâîðåíî, ê ñòîëáèêó âîçäóõà ìîæíî ïðèìåíèòü
çàêîí Áîéëÿ – Ìàðèîòòà:

begin{displaymath} P_1V_1 = P_2V_2,, end{displaymath}(4)


ãäå $P_1$ è $V_1$ — äàâëåíèå è îáúåì
âîçäóõà â ïåðâîì ñîñòîÿíèè; $P_2$ è $V_2$ — òî æå âî
âòîðîì ñîñòîÿíèè.

begin{center}vbox{defbasepath{D:/html/work/link1/metod} defmetdir{met8} getpic{M21}}end{center}

Äëÿ îòâåòà íà âîïðîñ çàäà÷è íóæíî âûðàçèòü ïàðàìåòðû ãàçà ÷åðåç
èçâåñòíûå â îáùåì âèäå
âåëè÷èíû – $H$ è $ell$. Îáîçíà÷èì èñêîìóþ
äëèíó ñòîëáèêà ðòóòè ÷åðåç $X$.  ïåðâîì
ñîñòîÿíèè ñòîëáèê âîçäóõà äëèíîé $ell/2$, òî åñòü îáúåìîì
$V_1={Sellover 2}$ ($S$ – ïëîùàäü
ñå÷åíèÿ òðóáêè), íàõîäèëñÿ ïîä àòìîñôåðíûì äàâëåíèåì, òàê êàê òðóáêà
áûëà îòêðûòà ñâåðõó.
Âûðàçèì àòìîñôåðíîå äàâëåíèå: $P_1 = rho gH$,
ãäå $rho$ – ïëîòíîñòü ðòóòè. Òàêèì îáðàçîì,

begin{displaymath} P_1V_1 = rho gH{Sellover 2},. end{displaymath}(5)


Âî âòîðîì ñîñòîÿíèè äëèíà ñòîëáèêà âîçäóõà ñòàëà ðàâíîé $(ell-X)$, à åãî îáúåì $V_2=S(ell-X)$.
Äàâëåíèå âîçäóõà â ñóììå ñ äàâëåíèåì îñòàâøåãîñÿ ñòîëáèêà ðòóòè âûñîòîé
$X$ óðàâíîâåøèâàåòñÿ
àòìîñôåðíûì äàâëåíèåì, äåéñòâóþùèì ñîãëàñíî çàêîíó Ïàñêàëÿ íà íèæíèé
îòêðûòûé êîíåö òðóáêè:
$P_2+rho gX=rho gH$, îòêóäà äàâëåíèå

begin{displaymath}P_2=rho g(H-X) {è}end{displaymath}

begin{displaymath} P_2V_2 = rho g(H-X)S(ell-X),. end{displaymath}(6)


Ïîäñòàâèâ âûðàæåíèÿ (5 è 6)
â èñõîäíîå óðàâíåíèå (4) è
ñîêðàòèâ íà $g, S, rho$, ïîëó÷èì êâàäðàòíîå óðàâíåíèå
îòíîñèòåëüíî $X$:

begin{displaymath} X^2 - (H+ell)X+{ell Hover 2}=0,. end{displaymath}(7)


Äâà êîðíÿ ýòîãî óðàâíåíèÿ:

begin{displaymath}X_{1,2} = {(H+ell)pm sqrt{(H+ell)^2-2ell H}over 2}={(H+ell)pm sqrt{H^2+ell^2}over 2},.end{displaymath}

Ìàòåìàòè÷åñêàÿ ÷àñòü çàäà÷è âûïîëíåíà: íàéäåíû êîðíè êâàäðàòíîãî
óðàâíåíèÿ. Îäíàêî
óñëîâèþ ôèçè÷åñêîé çàäà÷è êîðåíü óðàâíåíèÿ ñî çíàêîì “+” íå
óäîâëåòâîðÿåò, òàê êàê äëèíà
ñòîëáèêà ðòóòè â ýòîì ñëó÷àå ïðåâûøàåò äëèíó òðóáêè $ell$. Ïîýòîìó

$X={(H+ell)-sqrt{H^2+ell^2}over 2}$. Âèäíî, ÷òî $X$ ïîëó÷èòñÿ â åäèíèöàõ äëèíû.
 ÷èñëîâîì âàðèàíòå ðåøåíèÿ ïîäîáíîé çàäà÷è $H$ è $ell$ íóæíî ïîäñòàâëÿòü â îäèíàêîâûõ
åäèíèöàõ äëèíû, íàïðèìåð, â ì.

Îòâåò: èñêîìàÿ äëèíà ñòîëáèêà âûðàæàåòñÿ òàê:

begin{displaymath}X={(H+ell)-sqrt{H^2+ell^2}over 2},.end{displaymath}


Ïðèìåð 1.3. Â ñòåêëÿííîì ñôåðè÷åñêîì ñîñóäå ñ
âíóòðåííèì äèàìåòðîì $3,{ñì}$ íàõîäèòñÿ àçîò,
äàâëåíèå êîòîðîãî ïðè òåìïåðàòóðå $-190^circ C$
ðàâíî 1,33 Ïà. Íà ñòåíêàõ âíóòðè ñîñóäà èìååòñÿ
ìîíîìîëåêóëÿðíûé (òîëùèíîé â îäíó ìîëåêóëó) ñëîé àäñîðáèðîâàííîãî, òî
åñòü ïîãëîùåííîãî
ïîâåðõíîñòíûì ñëîåì, àçîòà. Îäíà ìîëåêóëà çàíèìàåò ïëîùàäü
$10^{-15},{ñì}^2$. Íàéòè
äàâëåíèå àçîòà â ñîñóäå ïðè òåìïåðàòóðå $427^circ C$,
ïðè êîòîðîé îí ïîëíîñòüþ äåñîðáèðóåòñÿ
ñî ñòåíîê.

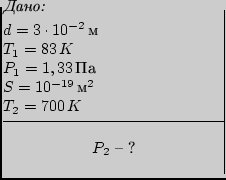hbox to 0.4hsizeÐåøåíèå.
Àçîò ïðè òàêîì íèçêîì äàâëåíèè ìîæíî ðàññìàòðèâàòü êàê èäåàëüíûé ãàç è
ïðèìåíèòü ñîîòâåòñòâóþùóþ òåîðèþ.
Èñêîìîå äàâëåíèå $P_2$ áóäåò ñêëàäûâàòüñÿ èç äàâëåíèÿ
ãàçà, ïåðâîíà÷àëüíî íàõîäèâøåãîñÿ
â ñîñóäå $P_2'$, è äàâëåíèÿ $P_2''$, êîòîðîå ñîçäàäóò
ìîëåêóëû, ïåðåøåäøèå ñî ñòåíîê
â cocóä ïðè òåìïåðàòóðå $T_2$:

begin{displaymath} P_2 = P_2'+P_2'',. end{displaymath}(8)


Âûðàçèì äàâëåíèå $P_2'$, ó÷èòûâàÿ, ÷òî ïîâûøåíèå
òåìïåðàòóðû ïðîèñõîäèò ïðè ïîñòîÿííîì
îáúåìå. Ñîãëàñíî çàêîíó Øàðëÿ:

begin{displaymath}{P_1over T_1}={P_2'over T_2},,end{displaymath}


begin{displaymath} {îòêóäàquadquad} P_2' = P_1{T_2over T_1},. end{displaymath}(9)


Âèäíî, ÷òî åäèíèöà èçìåðåíèÿ $P_2'$ ïîëó÷àåòñÿ òàêàÿ æå,
êàê $P_1$ – Ïà.

Äàâëåíèå $P_2''$ âûðàçèì èç îñíîâíîãî óðàâíåíèÿ
êèíåòè÷åñêîé òåîðèè èäåàëüíîãî ãàçà:

begin{displaymath} P_2'' = nkT_2={Nover V}kT_2,, end{displaymath}(10)


ãäå $N$ – îáùåå ÷èñëî äåñîðáèðîâàííûõ ìîëåêóë, $n$ – èõ êîíöåíòðàöèÿ,
$k$ – ïîñòîÿííàÿ Áîëüöìàíà, $V$ – îáúåì ñîñóäà:
$V={pi d^3over 6}$.
Îáùåå ÷èñëî ìîëåêóë, ïåðåøåäøèõ ñî ñòåíîê â ñîñóä, ìîæíî âûðàçèòü êàê
îòíîøåíèå
ïëîùàäè âíóòðåííåé ïîâåðõíîñòè ñôåðè÷åñêîãî ñîñóäà $pi d^2$
ê ïëîùàäè îäíîé ìîëåêóëû: $N={pi d^2over S}$. Îêîí÷àòåëüíî äëÿ äàâëåíèÿ $P_2''$ ïîëó÷èì:

begin{displaymath} P_2'' = {pi d^2cdot 6cdot kT_2over Spi d^3}={6kT_2over Sd},. end{displaymath}(11)


Ïðîâåðêà åäèíèö èçìåðåíèÿ èñêîìîé âåëè÷èíû:

begin{displaymath}[P_2'']={{Äæ}cdot{Ê}over{Ê}cdot{ì}^2cdot{ì}}= {{Í}cdot{ì}over{ì}^3}={{Í}over{ì}^2}={Ïà},.end{displaymath}

Ïîëó÷åíà åäèíèöà äàâëåíèÿ, òî åñòü âûðàæåíèå â îáùåì âèäå ïðàâèëüíî.

Òàêèì îáðàçîì,

begin{displaymath} P_2 = P_1 {T_2over T_1}+{6kT_2over Sd},. end{displaymath}(12)


Âû÷èñëåíèÿ:

begin{displaymath}P_2=left ({1,3cdot 7cdot 10^2over 83}+{6cdot 1,38cdot 1... ...7cdot 10^{2}over 10^{-19}cdot 3cdot 10^{-2}}right ),{Ïà}=end{displaymath}

begin{displaymath}=left ( 11,22+{6cdot 1,38 cdot 7over 3}right),{Ïà}=(11,22+19,32),{Ïà}=30,54,{Ïà},.end{displaymath}

Âèäíî, ÷òî ïî ïîðÿäêó âåëè÷èíû äåéñòâèå îáîèõ ôàêòîðîâ: ðîñòà äàâëåíèÿ
ñ ïîâûøåíèåì
òåìïåðàòóðû è óâåëè÷åíèÿ êîíöåíòðàöèè ìîëåêóë â ñîñóäå — ñîãëàñóåòñÿ
ïî ïîðÿäêó âåëè÷èí.
Âòîðîé ôàêòîð â äàííîì ñëó÷àå îêàçûâàåò áîëüøåå äåéñòâèå.

Îòâåò: äàâëåíèå àçîòà â ñîñóäå ñòàíåò ðàâíûì 30,54 Ïà.

Ïðèìåð 1.4. Íàéòè ñðåäíåå ÷èñëî âñåõ ïàðíûõ
ñòîëêíîâåíèé â ñåêóíäó ìîëåêóë êèñëîðîäà,
íàõîäÿùèõñÿ â îáúåìå $1,{ñì}^3$ ïðè òåìïåðàòóðå $17^circ C$ è äàâëåíèè 666,5
Ïà.

hbox to 0.4hsizeÐåøåíèå.
Ñîãëàñíî ÌÊÒ èäåàëüíîãî ãàçà ñðåäíåå ÷èñëî ñòîëêíîâåíèé â ñåêóíäó

îäíîé
ìîëåêóëû

ðàâíî:

begin{displaymath} overline{Z} = sqrt{2}pi d^2noverline{v},, end{displaymath}(13)


ãäå $d$ – ýôôåêòèâíûé äèàìåòð ìîëåêóëû, $n$ – êîíöåíòðàöèÿ ãàçà, $overline{v}$
–
ñðåäíÿÿ àðèôìåòè÷åñêàÿ ñêîðîñòü ìîëåêóë.

Åñëè ó÷èòûâàòü òîëüêî ïàðíûå

ñòîëêíîâåíèÿ, ÷èñëî âñåõ ñòîëêíîâåíèé â
ñåêóíäó áóäåò áîëüøå â ${Nover 2}={nVover 2}$ ðàç, ãäå $N$ – îáùåå
÷èñëî ìîëåêóë.

Òîãäà èñêîìîå ÷èñëî ñòîëêíîâåíèé âûðàçèòñÿ òàê:

begin{displaymath} overline{Z}={sqrt{2}pi d^2overline{v}n^2Vover 2},. end{displaymath}(14)


Äàëåå ñëåäóåò âûðàçèòü êîíöåíòðàöèþ ãàçà èç îñíîâíîãî óðàâíåíèÿ
êèíåòè÷åñêîé òåîðèè
èäåàëüíîãî ãàçà: $p=nkT$, à ñðåäíþþ àðèôìåòè÷åñêóþ ñêîðîñòü
— ÷åðåç ïàðàìåòðû ãàçà:
$overline{v}=sqrt{8RToverpimu}$, ãäå $R$ — óíèâåðñàëüíàÿ (ìîëÿðíàÿ) ãàçîâàÿ ïîñòîÿííàÿ.
Ïîñëå ïîäñòàíîâêè äëÿ èñêîìîé âåëè÷èíû ïîëó÷àåòñÿ:

begin{displaymath} overline{Z}=2left({dPover kT}right)^2Vsqrt{pi RTovermu},. end{displaymath}(15)


 ýòîì âûðàæåíèè âñå, êðîìå äèàìåòðà ìîëåêóëû, èçâåñòíî. Ýòî ÷èñëî
âçÿòî èç òàáëèöû.

Ïðîâåðêà åäèíèöû èçìåðåíèÿ èñêîìîé âåëè÷èíû:

begin{displaymath}[overline{Z}]={{ì}^2cdot{Í}^2cdot{Ê}^2cdot{ì}^3cdot{Äæ}^... ... 2}over{ñ}cdot{ì}^{3over 2}cdot{êã}^{1over 2}}={ñ}^{-1},.end{displaymath}

Íàèìåíîâàíèå $c^{-1}$ ñîîòâåòñòâóåò ÷èñëó ñòîëêíîâåíèé â
ñåêóíäó.

Âû÷èñëåíèÿ:

begin{displaymath}overline{Z}={2cdot 12,25cdot 10^{-20}cdot (666,5)^2cdot ... ...over327cdot 10^{-3}},{ñ}^{-1} =3,3cdot 10^{24},{ñ}^{-1},.end{displaymath}

Îòâåò: ïðè óêàçàííûõ óñëîâèÿõ ïðîèñõîäèò
$3,3cdot 10^{24}$ ïàðíûõ ñòîëêíîâåíèé ìîëåêóë
â ñåêóíäó. Ýòî ÷èñëî çàâèñèò îò ïàðàìåòðîâ ñîñòîÿíèÿ ($P, T$), îáúåìà ãàçà è åãî
èíäèâèäóàëüíûõ õàðàêòåðèñòèê: äèàìåòðà ìîëåêóëû è ìîëÿðíîé ìàññû.

Ïðèìåð 1.5. Ðàññòîÿíèå ìåæäó ñòåíêàìè ñîñóäà ðàâíî $8,{ìì}$. Ïðè êàêîì äàâëåíèè âÿçêîñòü
ãàçà, íàõîäÿùåãîñÿ ìåæäó íèìè, íà÷íåò óìåíüøàòüñÿ ïðè îòêà÷êå?
Òåìïåðàòóðà ãàçà ðàâíà
$17^circ C$. Äèàìåòð ìîëåêóëû ñîñòàâëÿåò
$3cdot 10^{-10},{ì}$.

Читайте также:  Законы пирогова о сосудах

hbox to 0.4hsizeÐåøåíèå.
Òåîðåòè÷åñêè âÿçêîñòü ãàçà ïðè íå ñëèøêîì íèçêèõ äàâëåíèÿõ 
íå çàâèñèò îò íåãî:

begin{displaymath} eta = {1over 3}overline{v}overline{lambda}rho,, end{displaymath}(16)


òàê êàê $overline{lambda}$ – ñðåäíÿÿ äëèíà ñâîáîäíîãî ïðîáåãà ìîëåêóë îáðàòíî
ïðîïîðöèîíàëüíà äàâëåíèþ ïðè ïîñòîÿííîé òåìïåðàòóðå:

begin{displaymath} overline{lambda} = {1over sqrt{2}pi d^2n}={kTover sqrt{2}pi d^2P},, end{displaymath}(17)


à ïëîòíîñòü ãàçà $rho$ ïðÿìî ïðîïîðöèîíàëüíà äàâëåíèþ.
Âûðàæåíèå äëÿ ïëîòíîñòè èäåàëüíîãî ãàçà
ìîæíî ïîëó÷èòü èç óðàâíåíèÿ Êëàïåéðîíà – Ìåíäåëååâà:
$PV = {movermu}RT$, ó÷èòûâàÿ,
÷òî ïëîòíîñòü — ýòî ìàññà åäèíèöû îáúåìà:
$rho = {mover V}$. Ïîëó÷àåòñÿ, ÷òî
$rho = {mu Pover RT}$.

Ïðè íèçêîì äàâëåíèè ñðåäíÿÿ äëèíà ñâîáîäíîãî ïðîáåãà
ïåðåñòàåò
çàâèñåòü îò äàâëåíèÿ è îïðåäåëÿåòñÿ ðàçìåðàìè ñîñóäà:

begin{displaymath} overline{lambda} = ell,. end{displaymath}(18)


Ìîëåêóëû äâèæóòñÿ îò ñòåíêè ê ñòåíêå, íå ñòàëêèâàÿñü ìåæäó ñîáîé.
Âÿçêîñòü ãàçà íà÷íåò
óìåíüøàòüñÿ ïðè äàëüíåéøåé îòêà÷êå ñîñóäà çà ñ÷åò óìåíüøåíèÿ
êîíöåíòðàöèè ìîëåêóë
(ïëîòíîñòè ãàçà).

Äëÿ ðåøåíèÿ çàäà÷è íóæíî ïðèðàâíÿòü âûðàæåíèå äëÿ ñðåäíåé äëèíû
ñâîáîäíîãî
ïðîáeãa ìîëåêóë $overline{lambda}$ ðàññòîÿíèþ ìåæäó ñòåíêàìè ñîñóäà:

begin{displaymath}ell = {kTover sqrt{2}pi d^2P},end{displaymath}



è âûðàçèòü äàâëåíèå. Ïîëó÷àåì:

begin{displaymath} P = {kTover sqrt{2}pi d^2ell},. end{displaymath}(19)


 ýòîì âûðàæåíèè äëÿ äàâëåíèÿ âñå èçâåñòíî.

Ïðîâåðêà íàèìåíîâàíèÿ åäèíèöû èçìåðåíèÿ:

begin{displaymath}[P]={{Äæ}cdot{Ê}over{Ê}cdot{ì}^2cdot{ì}}={{Äæ}over {ì}^3}={{Í}cdot{ì}over{ì}^3}={{Í}over{ì}^2}={Ïà},.end{displaymath}

Âûðàæåíèå äëÿ äàâëåíèÿ â îáùåì âèäå ïîëó÷åíî ïðàâèëüíî.

Âû÷èñëåíèÿ:

begin{displaymath}P={1,38cdot 10^{-23}cdot 290over sqrt{2}cdot 3,14cdot 9... ...290over sqrt{2}cdot 3,14cdot 9cdot 8},{Ïà}=1,26, {Ïà},.end{displaymath}

Ïîëó÷åííîå ÷èñëî çíà÷èòåëüíî ìåíüøå âåëè÷èíû àòìîñôåðíîãî äàâëåíèÿ. Äëÿ
äàííîãî ãàçà ïðè íåèçìåííîé
òåìïåðàòóðå îíî îïðåäåëÿåòñÿ òîëüêî ðàçìåðàìè ñîñóäà $ell$.

Îòâåò: ïðè äàâëåíèè 1,26 Ïà âÿçêîñòü ãàçà íà÷íåò óìåíüøàòüñÿ
ïðè îòêà÷êå.
Óêàçàíèå: ïîäîáíûì îáðàçîì ðåøàþòñÿ çàäà÷è, ñâÿçàííûå ñ
êîýôôèöèåíòîì òåïëîïðîâîäíîñòè
èäåàëüíîãî ãàçà:

begin{displaymath}chi = {1over 3}overline{v}overline{lambda}rho c_v,,end{displaymath}



ãäå $c_v$ – óäåëüíàÿ òåïëîåìêîñòü
ïðè ïîñòîÿííîì îáúåìå:

begin{displaymath}c_v={iover 2}{Rovermu} (i{ -- ÷èñëî ñòåïåíåé ñâîáîäû ìîëåêóëû}).end{displaymath}


Ïðèìåð 1.6. 10 ë àçîòà, íàõîäÿùåãîñÿ ïîä äàâëåíèåì $10^5,{Ïà}$, ðàñøèðÿþòñÿ âäâîå.
Íàéòè êîíå÷íîå äàâëåíèå è ñîâåðøåííóþ ãàçîì ðàáîòó â ñëó÷àÿõ
èçîáàðè÷åñêîãî,
èçîòåðìè÷åñêîãî è àäèàáàòè÷åñêîãî ïðîöåññîâ. Ìîëåêóëû àçîòà èìåþò ïÿòü
ñòåïåíåé ñâîáîäû.

hbox to 0.4hsizeÐåøåíèå.
Ïðèìåì àçîò â äàííûõ óñëîâèÿõ çà èäåàëüíûé ãàç.
1. Ïðè èçîáàðè÷åñêîì ïðîöåññå äàâëåíèå ãàçà íå ìåíÿåòñÿ, ïîýòîìó $P_2=P_1$.
Ýëåìåíòàðíàÿ ðàáîòà ðàñøèðåíèÿ ðàâíà â îáùåì ñëó÷àå $PdV$, ãäå $P$ – äàâëåíèå,
$dV$ – áåñêîíå÷íî ìàëûé îáúåì. Ïîëíàÿ ðàáîòà íàõîäèòñÿ ïóòåì
èíòåãðèðîâàíèÿ, è âåëè÷èíà
eå çàâèñèò îò âèäà ïðîöåññà.

Ïðè èçîáàðè÷åñêîì ïðîöåññå

begin{displaymath} A_1=intlimits_{V_1}^{V_2}{PdV}=P(V_2-V_1),. end{displaymath}(20)


Ïðîâåðèì åäèíèöó èçìåðåíèÿ ðàáîòû:

begin{displaymath}[A]= {{Í}cdot {ì}^3over {ì}^2}={Í}cdot{ì}={Äæ},.end{displaymath}

2.  èçîòåðìè÷åñêîì ïðîöåññå òåìïåðàòóðà îñòàåòñÿ ïîñòîÿííîé, à
äàâëåíèÿ è îáúåìû â äâóõ
ñîñòîÿíèÿõ èäåàëüíîãî ãàçà ñâÿçàíû çàêîíîì Áîéëÿ – Ìàðèîòòà: $P_1V_1=P_2V_2$, îòêóäà
$P_2'={P_1V_1over V_2}$. Âèäíî, ÷òî çäåñü äëÿ åäèíèöû íåèçâåñòíîãî äàâëåíèÿ
ïîëó÷àåòñÿ
Ïà (ïàñêàëü).

Ðàáîòà èçîòåðìè÷åñêîãî ðàñøèðåíèÿ ðàññ÷èòûâàåòñÿ òàê:

begin{displaymath}A_2=int{PdV}=intlimits_{V_1}^{V_2}{{m over mu}RT{dVover V}}={movermu}RTln{V_2 over V_1},.end{displaymath}



Çäåñü äàâëåíèå âûðàæåíî èç óðàâíåíèÿ Êëàïåéðîíà – Ìåíäåëååâà.
Òåìïåðàòóðà
íåèçâåñòíà, ïîýòîìó, ïðèìåíèâ åùå ðàç óðàâíåíèå Êëàïåéðîíà –
Ìåíäåëååâà, ïîëó÷èì âûðàæåíèå
äëÿ èñêîìîé ðàáîòû ÷åðåç èçâåñòíûå â óñëîâèè âåëè÷èíû:

begin{displaymath} A_2 = P_1V_1ln{V_2over V_1},. end{displaymath}(21)


Ðåçóëüòàò íå èçìåíèòñÿ, åñëè ïîäñòàâèòü êîíå÷íûå äàâëåíèå è îáúåì $P_2$ è
$V_2$ èëè âìåñòî îòíîøåíèÿ ${V_2over V_1}$ âçÿòü ${P_1over P_2}$.

3. Êîíå÷íîå äàâëåíèå àäèàáàòè÷åñêîãî ðàñøèðåíèÿ âûðàçèì èç óðàâíåíèÿ
Ïóàññîíà:

begin{displaymath}P_2''=P_1left({V_1over V_2}right)^gamma,, {ãäå }gamma={C_pover C_V}={i+2over i}end{displaymath}



($i$ – ÷èñëî ñòåïåíåé ñâîáîäû ìîëåêóëû).

Ðàáîòà â ýòîì ïðîöåññå ñîâåðøàåòñÿ çà ñ÷åò óáûëè âíóòðåííåé ýíåðãèè
ãàçà:

begin{displaymath}A_3=-Delta u={movermu}C_V(T_1-T_2)={movermu}C_V T_1 left(1-{T_2over T_1}right),,end{displaymath}



ãäå $C_V$ – ìîëÿðíàÿ òåïëîåìêîñòü ïðè ïîñòîÿííîì îáúåìå:

begin{displaymath}C_V={iover 2}R={Rover gamma-1},.end{displaymath}

begin{center}vbox{getpic{M22}}end{center}

 ýòîé çàäà÷å òåìïåðàòóðû íå çàäàíû, ïîýòîìó îòíîøåíèå òåìïåðàòóð
ñëåäóåò çàìåíèòü îòíîøåíèåì
îáúåìîâ
${T_2over T_1}=left({V_1over V_2}right)^{gamma-1}$ è âîñïîëüçîâàòüñÿ
óðàâíåíèåì ñîñòîÿíèÿ èäåàëüíîãî ãàçà:

begin{displaymath}A_3={movermu}{Rover(gamma-1)}T_1left(1-{T_2over T_1}ri... ...amma-1)} left(1-left({V_1over V_2}right)^{gamma-1}right)=end{displaymath}


begin{displaymath} ={1overgamma-1}(P_1V_1-P_2''V_2),. end{displaymath}(22)


Çäåñü âñå èçâåñòíî, êîíå÷íîå äàâëåíèå ìîæíî ðàññ÷èòàòü îòäåëüíî.

Âû÷èñëåíèÿ:

  1. $P_2=P_1=10^{5},{Ïà},;quad A_1=10^{5}cdot 10^{-2},{Äæ}=10^{3},{Äæ}$.
  2. $P_2'={10^{5}cdot 10^{-2}over 2cdot 10^{-2}},{Ïà}=5cdot 10^{4},{Ïà},;$

    $A_2=10^{5}cdot 10^{-2}ln{2cdot 10^{-2}over 10^{-2}},{Äæ}=10^{3}ln{2},{Äæ}= 6,9cdot 10^2,{Äæ}.$

  3. $P_2''= 10^{5}cdot 0,5^{1,4},{Ïà}=3,8cdot 10^4,{Ïà},;$

    $A_3={1over 0,4}(10^3-760),{Äæ}=600,{Äæ},.$

Òàêèì îáðàçîì, íàèáîëüøåå èçìåíåíèå äàâëåíèÿ ïðîèñõîäèò ïðè
àäèàáàòè÷åñêîì ðàñøèðåíèè,
à íàèáîëüøàÿ ðàáîòà ñîâåðøàåòñÿ ïðè èçîáàðè÷åñêîì. Êà÷åñòâåííî
ðåçóëüòàòû ïðåäñòàâëåíû
íà ðèñóíêå. Ïëîùàäè ôèãóð ïîä ãðàôèêàìè ïðîöåññîâ ïîçâîëÿþò ñóäèòü î
ñîîòíîøåíèè ñîâåðøåííîé
ðàáîòû.

Îòâåò:
$10^{5},{Ïà},, 10^{3},{Äæ},; 5cdot 10^{4},{Ïà},, 690,{Äæ},; 3,8cdot 10^4,{Ïà},, 600,{Äæ}.$

Ïðèìåð 1.7. Õîëîäèëüíàÿ ìàøèíà, ðàáîòàþùàÿ ïî
îáðàòíîìó öèêëó Êàðíî, ïåðåäàåò òåïëîòó îò
õîëîäèëüíèêà ñ âîäîé ïðè òåìïåðàòóðå $0^circ C$
êèïÿòèëüíèêó ñ âîäîé ïðè òåìïåðàòóðå $100^circ$C.
Êàêóþ ìàññó âîäû íóæíî çàìîðîçèòü â õîëîäèëüíèêå, ÷òîáû ïðåâðàòèòü â
ïàð 1 êã âîäû â
êèïÿòèëüíèêå? Óäåëüíàÿ òåïëîòà ïàðîîáðàçîâàíèÿ âîäû ïðè $100^circ$Ñ ðàâíà
$2,26cdot 10^6,{Äæ/êã}$. Óäåëüíàÿ òåïëîòà ïëàâëåíèÿ ëüäà ðàâíà
$3,35cdot 10^5,{Äæ/êã}$.

hbox to 0.4hsizeÐåøåíèå.
Õîëîäèëüíàÿ ìàøèíà çà ñ÷åò âíåøíåé ðàáîòû îòíèìàåò íåêîòîðîå êîëè÷åñòâî
òåïëîòû $Q_2$
îò ìåíåå íàãðåòîãî òåëà ïðè òåìïåðàòóðå $T_2$ è
ïåðåäàåò òåïëîòó $Q_1$ áîëåå íàãðåòîìy òåëó
ïðè òåìïåðàòóðå $T_1$.
Êîýôôèöèåíò ïîëåçíîãî äåéñòâèÿ åå
$eta={Aover Q_1}={Q_1-Q_2over Q_1}$.

Òàêîå æå ñîîòíîøåíèå ñïðàâåäëèâî è äëÿ òåïëîâîé ìàøèíû, ñîâåðøàþùåé
ðàáîòó çà ñ÷åò ÷àñòè
òåïëîòû, âçÿòîé ó áîëåå íàãðåòîãî òåëà.

Íàèáîëüøèé êîýôôèöèåíò ïîëåçíîãî äåéñòâèÿ ñîîòâåòñòâóåò èäåàëüíîìó
(òåîðåòè÷åñêîìó) öèêëó Êàðíî.
 ýòîì ñëó÷àå
$eta={Q_1-Q_2over Q_1}={T_1-T_2over T_1}$, òî åñòü êïä
îïðåäåëÿåòñÿ òîëüêî
òåìïåðàòóðàìè íàãðåâàòåëÿ (òåëà ïðè òåìïåðàòóðå $T_1$) è
õîëîäèëüíèêà ($T_2$). Ñ ïîìîùüþ
ýòîãî ñîîòíîøåíèÿ ðåøàåòñÿ áîëüøèíñòâî çàäà÷, ñâÿçàííûõ ñ ðàáîòîé
òåïëîâûõ è õîëîäèëüíûõ ìàøèí.
 ðåàëüíûõ ìàøèíàõ êïä çíà÷èòåëüíî ìåíüøå, ÷åì
${T_1-T_2over T_1}$.

 äàííîé çàäà÷å êîëè÷åñòâî òåïëîòû $Q_1$, ïåðåäàâàåìîå áîëåå
íàãðåòîìó òåëó, ðàâíî $rm_1$,
à êîëè÷åñòâî òåïëîòû $Q_2$, âçÿòîå îò ìåíåå íàãðåòîãî òåëà,
ðàâíî $lambda m_2$, ïîýòîìó
ñïðàâåäëèâî ðàâåíñòâî:

begin{displaymath} {rm_1-lambda m_2over rm_1}={T_1-T_2over T_1},, end{displaymath}(23)


êîòîðîå ìîæíî ïðåîáðàçîâàòü òàê:

begin{displaymath}{lambda m_2over rm_1}={T_2over T_1},,end{displaymath}


begin{displaymath} {îòêóäà}quad m_2={rm_1T_2overlambda T_1},. end{displaymath}(24)


Ïðîâåðêà íàèìåíîâàíèÿ åäèíèöû:

begin{displaymath}[m]= {{Äæ}cdot {êã}cdot {Ê}cdot {êã}over{êã}cdot{Äæ}cdot {Ê}}={êã},.end{displaymath}

Âû÷èñëåíèÿ:

begin{displaymath}m_2={2,26cdot 10^{6}cdot 1cdot 273over 3,35cdot 10^{5}c... ...73},{êã}={2,26cdot 2730over 3,35cdot 373},{êã}=4,94,{êã}.end{displaymath}

Îòâåò: ÷òîáû èñïàðèòü 1 êã âîäû â êèïÿòèëüíèêå ïðè çàäàííûõ
óñëîâèÿõ, íóæíî
çàìîðîçèòü 4,94 êã âîäû â õîëîäèëüíèêå.

Äàëåå: 1.2. 
Çàäà÷è äëÿ ñàìîñòîÿòåëüíîãî
Ââåðõ: 1. 
Ìîëåêóëÿðíàÿ ôèçèêà è
Íàçàä: 1. 
Ìîëåêóëÿðíàÿ ôèçèêà è

ßÃÏÓ, Öåíòð èíôîðìàöèîííûõ
òåõíîëîãèé îáó÷åíèÿ

2005-09-21<

Предыдущая статья
Влияние натурального кофе на сосуды
Следующая статья
Как на юге руси называли сосуды для ...
© Про сосуды от врачей отеля