В сосуде объемом v при давлении p и температуре t
Страница 5 из 12
5.81. В сосуде объемом V = 0,1 МПа находится азот при давлении p = 0,1 МПа. Какое количество теплоты Q надо сообщить азоту, чтобы: а) при p = const объем увеличился вдвое; б) при V = const давление увеличилось вдвое?
5.82. В закрытом сосуде находится масса m = 14г азота при давлении pх = 0,1 МПа и температуре t = 27° С. После нагревания давление в сосуде повысилось в 5 раз. До какой температуры t2 был нагрет газ? Найти объем V сосуда и количество теплоты Q, сообщенное газу.
5.83. Какое количество теплоты Qнадо сообщить массе
m = 12г кислорода, чтобы нагреть его на dt= 50° С при p = const ?
5.84. На нагревание массы m = 40 г кислорода от температуры t1 = 16° С до t2 = 40° С затрачено количество теплоты Q = 628Дж. При каких условиях нагревался газ (при постоянном объеме или при постоянном давлении)?
5.85. В закрытом сосуде объемом V = 10 л находится воздух при давлении p = 0,1 МПа. Какое количество теплоты Qнадо сообщить воздуху, чтобы повысить давление в сосуде в 5 раз?
5.86. Какую массу m углекислого газа можно нагреть при p = const от температуры t1 =20° С до t2=100° С количеством теплоты Q = 222Дж? На сколько при этом изменится кинетическая энергия одной молекулы?
5.87. В закрытом сосуде объем V = 2 л находится азот, плотность которого р = 1,4 кг/м3 Какое количество теплоты Q надо сообщить азоту, чтобы нагреть его на dT = 100 К?
5.88. Азот находится в закрытом сосуде объемом V = 3 л при температуре t1=27° С и давлении p1 = 0,ЗМПа. После нагревания давление в сосуде повысилось до p2=2,5МПа. Найти температуру t2азота после нагревания и количество теплоты Q, сообщенное азоту.
5.89. Для нагревания некоторой массы газа на dt1 =50° С при p = const необходимо затратить количество теплоты Q{= 670 Дж.
Если эту же массу газа охладить на dt2 = 100° С при V = const, то выделяется количество теплоты Q2=1005Дж. Какое число степеней свободы i имеют молекулы этого газа?
5.90. Масса m = 10 г азота находится в закрытом сосуде при температуре t1 = 7° С. Какое количество теплоты Qнадо сообщить азоту, чтобы увеличить среднюю квадратичную скорость его молекул вдвое? Во сколько раз при этом изменится температура газа? Во сколько раз при этом изменится давление газа на стенки сосуда?
5.91. Гелий находится в закрытом сосуде объемом V = 2 л при температуре t1 = 20° С и давлении p1= 100 кПа. Какое количество теплоты Q надо сообщить гелию, чтобы повысить его температуру на dt = 100° С? Каковы будут при новой температуре средняя квадратичная скорость его молекул, давление p2, плотность p2гелия и энергия теплового движения W его молекул?
5.92. В закрытом сосуде объемом V = 2 л находится масса m азота и масса m аргона при нормальных условиях. Какое количество теплоты Q надо сообщить, чтобы нагреть газовую смесь на dt = 100°С?
5.93. Найти среднюю арифметическую v, среднюю квадратичную sqr(v2)и наиболее вероятную vв скорости молекул газа, который при давлении p = 40 кПа имеет плотность p = 0,3 кг/м.
5.94. При какой температуре Т средняя квадратичная скорость молекул азота больше их наиболее вероятной скорости на dv = 50 м/с?
5.95. Какая часть молекул кислорода при t = 0° С обладает скоростями v от 100 до 110 м/с?
5.96. Какая часть молекул азота при t = 150° С обладает скоростями v от 300 до 325 м/с?
5.97. Какая часть молекул водорода при t = 0° С обладает скоростями v от 2000 до 2100 м/с?
5.98. Во сколько раз число молекул dN1, скорости которых лежат в интервале от vB до vB + dv , больше числа молекул dN2,
скорости которых лежат в интервале от sqr(v2)до sqr(v2) + dv ?
5.99. Какая часть молекул азота при температуре Т имеет скорости, лежащие в интервале от vB до vB + dv , где dv = 20 м/с.
если: а) Т = 400 К; б) Т = 900 К?
5.100. Какая часть молекул азота при температуре t = 150° С имеет скорости, лежащие в интервале от v1=300m/c до
v2 = 800 м/с?
Источник
8. Молекулярно-кинетическая теория
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
В сосуде объёмом 2 л находится 10 г идеального газа при давлении 1 атм. и температуре 300 К. Во втором сосуде объёмом 4 л находится 20 г того же газа при давлении 2 атм. Чему равна температура газа во втором сосуде? (Ответ дайте в кельвинах.)
Уравнение состояния газа: [pV=nu RT=dfrac{m}{mu}RT] где (p) — давление газа, (V) — объем, занимаемый газом, (nu) — количество вещества, (R) — универсальная газовая постоянная, (T) — температура газа, (m) — масса газа, (mu) — молярная масса газа.
Для первого сосуда: [p_1V_1=dfrac{m_1}{mu}RT_1] Для второго сосуда: [p_2V_2=dfrac{m_2}{mu}RT_2] Поделим уравнения друг на друга: [dfrac{p_1V_1}{p_2V_2}=frac{m_1T_1}{m_2T_2}] [T_2=T_1cdotdfrac{m_1}{m_2}cdotdfrac{V_2}{V_1}cdotdfrac{p_2}{p_1}=300text{ К}cdotdfrac{1}{2}cdot2cdot2=600 text{ К}]
Ответ: 600
При уменьшении абсолютной температуры газа на 300 К давление уменьшилось в 5 раз. Какова начальная температура газа, если в ходе эксперимента количество вещества уменьшилось втрое, а объём оставался постоянным? (Ответ дайте в кельвинах.)
Запишем уравнение Менделеева-Клапейрона для первого и второго состояния: [begin{cases}
p_1 V=nu_1 R T_1\
p_2 V=nu_2 R T_2
end{cases}] где (p_1) и (p_2) — давления газа в первом и втором состояниях, V — объём газа, (nu_1) и (nu_2)— количество вещества в первом и втором состояниях, (R) — универсальная газовая постоянная, (T_1) и (T_2) — абсолютная температура в первом и втором состояниях.
Поделив одно уравнение на другое, получим: [dfrac{p_1}{p_2} = dfrac{nu_1 T_1}{nu_2 T_2}] Так как (nu_1 = 3nu_2) и (p_1 = 5p_2), то: [dfrac{5p_2}{p_2} = dfrac{3nu_2cdot T_1}{nu_2cdot T_2}
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
5=dfrac{3T_1}{T_2}
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
5T_2 = 3T_1] Так как (T_2 = (T_1 – 200) К), то: [5(T_1 – 300text{ K}) = 3T_1
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
5T_1 – 1500text{ K } = 3T_1
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
2T_1 = 1500text{ K }
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
T_1 = 750text{ K }]
Ответ: 750
На графиках приведены зависимости давления (p) и объема (V) от времени (t) для 1 моля идеального газа. Чему равна температура газа в момент (t) = 30 минут? (Ответ дайте в градусах Кельвина с точностью до 10 К.)
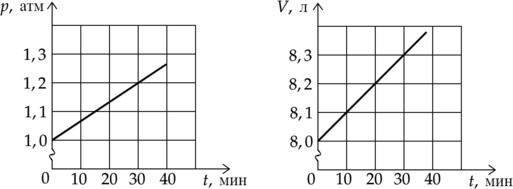
Уравнение состояния идеального газа: [displaystyle pV=nu RT,] где (p)—давление газа, (V)—объем газа, (nu) — количество вещества газа, (R) — универсальная газовая постоянная, (T) — температура. Выразим температуру газа: [T=dfrac{pV}{nu R}] Из графика найдем давление и объем в момент времени 30 мин:
(p=1,2cdot10^5) Па
(V=8,3cdot10^{-3}text{ м$^3$})
Подставим известные и найденные значения в формулу: [T=dfrac{1,2cdot10^5text{ Па}cdot8,3cdot10^{-3}text{ м$^3$}}{1text{ моль}cdot8,31text{ }dfrac{text{Дж}}{text{моль}}} approx 120 text{ К}]
Ответ: 120
В сосуде неизменного объёма находится разреженный газ в количестве 3 моль. Во сколько раз изменится давление газа в сосуде, если выпустить из него 1 моль газа, а абсолютную температуру газа уменьшить в 2 раза?
“Демоверсия 2019”
Запишем уравнение Клапейрона – Менделеева: [p1V=nu_1RT_1=3RT_1] [p_2V=nu_2RT_2=2Rdfrac{T_1}{2}=RT_1] [dfrac{p_1}{p_2}=dfrac{3RT_1}{RT_1}=3]
Ответ: 3
В сосуде неизменного объёма находится идеальный газ. Во сколько раз нужно увеличить количество газа в сосуде, чтобы после уменьшения абсолютной температуры газа в 2 раза его давление стало вдвое больше начального?
“Досрочная волна 2020 вариант 1”
Из уравнения Клапейрона –Менделеева: [pV=nu RT] чтобы давление ((p)) увеличилось в 2 раза, при уменьшении температуры ((T)) в 2 раза, количество вещества ((nu)) должно увеличится в 4 раза
Ответ: 4
В сосуде неизменного объема находится разреженный газ в количестве 4 моль. Во сколько раз нужно увеличить абсолютную температуру газа, чтобы после удаления из сосуда 3 моль газа, давление осталось неизменным?
“Основная волна 2020 ”
Уравнение Клайперона – Менделеева: [pV=nu RT] если удалить 3 моль газа, то количество вещества уменьшится в 4 раза (nu_1=dfrac{nu}{4}), следовательно, температуру надо увеличить в 4 раза.
Ответ: 4
Источник
Решебник
ВСЕ
ФИЗИКА
МАТЕМАТИКА
ХИМИЯ
Задача по физике – 3083
Сосуды объемом $V_{1} = 200 см^{3}$ и $V_{2} = 100 см^{3}$ соединены короткой трубкой, в которой имеется теплоизолируюшая пористая перегородка. С помощью этой перегородки в сосудах устанавливается одинаковое давление. Система находится при температуре $t_{0} = 27^{ circ} С$ и содержит газ при давлении $p_{0} = 10^{5} Па$. Какое давление установится в системе, если малый сосуд поместить в лед при температуре $t_{2} = 0^{ circ} С$, а большой – в пар при температуре $t_{1} = 100^{ circ} С$? Тепловым расширением сосудов можно пренебречь.
Подробнее
Задача по физике – 3084
В цилиндре с площадью сечения $S = 5 см^{2}$ под поршнем массой $M = 1 кг$ находится некоторый газ. При увеличении абсолютной температуры газа в $n = 1,5$ раза поршень поднимается вверх и упирается в уступы. При этом объем газа по сравнению с первоначальным увеличивается в $k = 1,2$ раза. Определить силу, с которой поршень давит на уступы. Атмосферное давление $p_{0} = 100 кПа$.
Подробнее
Задача по физике – 3085
На рис. представлен график изменения состояния идеального газа в осях V – р. Изобразить этот график в осях Т – V.

Подробнее
Задача по физике – 3086
Моль идеального газа участвует в процессе, изображенном на рис.. Продолжение отрезков прямых (1-2) и (3-4) проходят через начало координат, а кривые (1-4) и (2-3) являются изотермами. Изобразить этот процесс в координатах V – Т, (T – ось ординат) и найти объем $V_{3}$ если известны объемы $V_{1}$ и $V_{2} = V_{4}$.

Подробнее
Задача по физике – 3087
В запаянной с одного конца стеклянной трубке длиной $l = 0,9 м$ находится столбик воздуха, ограниченный сверху столбиком ртути высотой $h = 30 см$. Ртуть доходит до верхнего края трубки. Трубку осторожно поворачивают открытым концом вниз, при этом часть ртути выливается. Какова высота оставшегося столбика ртути? Атмосферное давление $p_{0} = 10^{5} Па$.

Подробнее
Задача по физике – 3088
Два баллона соединены трубкой с краном. В первом находится газ при давлении $p_{1} = 10^{5} Па$. во втором – при $p_{2} = 0,6 cdot 10^{5} Па$. Объем первого баллона $V_{1} = 10^{-3} м^{3}$, а второго $V_{2} = 3 cdot 10^{-3} м^{3}$. Какое давление установится в баллонах, если открыть кран? Температура постоянна. Объемом трубки можно пренебречь.
Подробнее
Задача по физике – 3089
В сосуде объемом $V = 3 cdot 10^{-2} м^{3}$ находится $m_{1} = 4 cdot 10^{-3} г$ гелия, $m_{2} = 70 cdot 10^{-3} г$ азота и $N = 5 cdot 10^{21}$ молекул водорода. Каково давление смеси, если ее температура $T = 300 К$?
Подробнее
Задача по физике – 3090
Сосуд объемом $V = 30 дм^{3}$ разделен на три равные части неподвижными полупроницаемыми перегородками. В левую часть вводят $m_{1} = 30 г$ водорода, в среднюю $m_{2} = 160 г$ кислорода и в правую $m_{3} = 70 г$ азота. Через левую перегородку может диффундировать только водород, через правую – водород и азот. Какое давление установится в каждой части сосуда,, если он поддерживается при постоянной температуре $T = 300 К$?
Подробнее
Задача по физике – 3091
На рис. изображен замкнутый процесс, который совершает некоторая масса кислорода. Известно, что максимальный объем, который занимал газ в этом процессе $V_{max} = 16,4 дм^{3}$. Определить массу газа и его объем в точке 1.

Подробнее
Задача по физике – 3092
Цилиндрический сосуд длиной $L = 1,5 м$, разделенный легким теплонепроницаемым поршнем, заполнен идеальным газом. В начальном состоянии объем левой части сосуда вдвое больше правой, а температура в обеих частях одинакова. На сколько переместится поршень, если температуру в правой части увеличить вдвое? Температура в левой части поддерживается постоянной.

Подробнее
Задача по физике – 3093
В сосуде с газом поддерживается температура $T_{1}$. Вне сосуда находится газ, давление которого – $p_{2}$, а температура – $T_{2}$. Чему равно давление газа внутри сосуда, если в его стенке имеется небольшое отверстие? Газы разрежены.
Подробнее
Задача по физике – 3094
Идеальный газ, масса которого $m$ и молярная масса $mu$, расширяется изобарно при некотором давлении. Начальная температура газа – $T_{1}$, конечная – $T_{2}$. Определить работу, совершаемую газом.
Подробнее
Задача по физике – 3095
Гелий (Не) нагревается при постоянном давлении. При этом ему сообщено $Q = 20 кДж$ теплоты. Определить изменение внутренней энергии газа и совершенную им работу.
Подробнее
Задача по физике – 3096
Температура некоторой массы $m$ идеального газа с молярной массой $mu$ меняется по закону $T = alpha V^{2}$, где $alpha = const > 0$. Найти работу, совершенную газом при увеличении объема от $V_{1}$ до $V_{2}$. Поглощается или выделяется теплота при таком процессе?
Подробнее
Задача по физике – 3097
При адиабатном сжатии 1 моля одноатомного газа внешними силами была совершена работа $A$. Во сколько раз увеличилась среднеквадратичная скорость молекул этого газа, если начальная температура газа равна $T_{1}$?
Подробнее
Источник
Пример 1.
Определите число молекул, содержащихся в 2 мм³ воды при 4°С.
Дано
Решение
V = 2·10-9 м³
T = 277 К
______________
N = ?
Число молекул определим, используя выражение
,
(1)
где ν – количество вещества, NA–число
Авогадро.
Учитывая, что ν=m/μ, где μ-молярная масса,
использовав (1), получим:
. (2)
Массу воды определим через плотность и объем : m=ρV.
Тогда формула (2) примет вид:
. (3)
Молярную массу молекулы H2O воды вычислим:
(2·1+1·16)·10-3
кг/моль=18·10-3 кг/моль.
Окончательно, из формулы (3) получаем N≈6,68·1019
.
Пример 2. Поршневой насос, объем
цилиндра которого равен 0,5л, соединен с баллоном емкостью 3л, содержащим
воздух при нормальном атмосферном давлении. Определите давление воздуха в
баллоне после 5 рабочих ходов поршня, если насос работает в режиме: а) нагнетательном,
б) разрежающем. Считать процесс изотермическим.
Дано
Решение
V1=5·10-4 м³
V2=3·10-3 м³
p0=1,013·10-3 Па
n=5
______________
pн, pр –?
а) Поршневой насос после n-рабочих
ходов в нагнетательном режиме заберет из атмосферы объем воздуха Vn=nV1
при давлении p0. Этот воздух, попадая в баллон, создает там
парциальное давление pn. Тогда, согласно закону
Бойля-Мариотта (по условию Т=const),
, отсюда . Искомое
давление воздуха в баллоне:
(1) |
б) По условию задачи воздух в баллоне занимает объем V2 при давлении р0. К концу первого
хода в разрежающем режиме та же масса воздуха займет объем V2+V1 при давлении p1.
Тогда по закону Бойля-Мариотта
, отсюда
В начале второго хода поршня объем и давление газа в баллоне
соответственно равны V2 и p1, а в конце хода – (V2+V1)
и p2, тогда
,
Следовательно, к концу n-го рабочего хода:
(2) |
Подставляя числовые значения в выражения (1) и (2), получим
pн=1,86·105 Па; pр=0,48·105
Па.
Пример 3. Идеальный газ находится
под давлением 250 кПа и занимает объем 2,5л при температуре 200К. Сначала газ
изохорно нагревают до температуры 400К. Затем, изотермически расширяя, газ
доводят до первоначального давления. После этого газ возвращают в начальное
состояние путем изобарного сжатия. Изобразите процесс графически на
рV-диаграмме. Определите давление p2 и объем V3.
Дано
Решение
p1=2,5·103 Па
V1=2,5·10-3 м³
Т1=200К,
Т2=400К
______________
p2 – ? V3-?
Построим график цикла:

При переходе газа из состояния 1 в состояние 2 осуществляется
изохорный процесс. Следовательно, по закону Шарля имеем p1/Т1=p2/Т2,
откуда
(1)
При переходе газа из состояния 3 в состояние 1 осуществляется
изобарный процесс. Тогда, согласно закону Гей-Люссака , отсюда .
Учитывая, что Т3=Т2 (точки 2 и 3
принадлежат одной изотерме), получим
. (2)
Произведем вычисления по формулам (1) и (2): p2=5·105
Па; V3= 5·10-3 м³.
Пример 4. Идеальный газ находится в
баллоне при 27°С и давлении 3·106 Па. Какой станет температура,
если из баллона будет выпущено 0,3 массы газа, а его давление понизится до
2·106 Па?
Дано
Решение
Т1=300К
p1=3·106 Па
p2=2·106 Па
k=0,3
____________________
Т2-?
Рассмотрим два состояния идеального газа. В первом состоянии
газ имеет массу m и характеризуется параметрами p1, V и T, во
втором состоянии он имеет массу и характеризуется параметрами p2,
V и Т2.
Параметры каждого из этих состояний связаны уравнением
Менделеева-Клапейрона:
,(1)
. (2)
Разделив почленно уравнение (1) на уравнение (2), имеем:
, откуда .
Произведем вычисления, получим Т2=286К
Пример 5. В закрытом сосуде объемом
2м³ находится 2г водорода и 32г кислорода при температуре 500К.
Определите: а) давление в сосуде, б) молярную массу смеси, в) плотность
смеси.
Дано
Решение
V= 2м³
Т= 500К
m1=0,002 кг
m2=0,032 кг
µ1=2·10-3кг/моль
µ2=32·10-3кг/моль
R=8,31Дж/моль·К
_______________
p-? µсм-? ρсм-?
Давление смеси определим по закону Дальтона
, (1)
где p1- давление водорода, p2-
давление кислорода.
Из уравнения Менделеева-Клапейрона:
, .(2)
С учетом (2) преобразуем выражение (1):
.(3)
Для определения молярной массы смеси используем (3) в виде
(4)
Обозначив через µсм молярную массу смеси,
запишем уравнение Менделеева-Клапейрона для смеси в виде
. (5)
Из выражений (4) и (5) получим
. (6)
Плотность смеси газов определим из:
, (7)
где m=m1+m2 – масса смеси газов. Объем смеси газов из(4):
.(8)
Решая совместно уравнения (7) и (8), получим:
.(9)
Произведем вычисления по формулам (3), (6) и (9):
р=4,2 кПа, µсм=17·10-3 кг/моль,
ρсм= 0,017кг/м³.
Пример 6. Чтобы не стать помехой
движению самолетов, олимпийский аэростат «Миша», наполненный гелием при p1=105Па
и температуре T0=300К, должен был подняться над Лужниками на высоту
h=1,5км, где плотность воздуха на 20% меньше, чем у поверхности Земли. Какова
масса M оболочки аэростата, если его объем V=500м3 (оболочку
считать герметичной и нерастяжимой).
Дано
Решение
V=500м3
p0=105Па
T0=300K
h=1.5×103м
mв=29×10-3кг/моль
mг=4×10-3кг/моль
_____________________
Mобл=?
Анализ
Предполагаем, что T =const, а V =const из условия. Условия
равновесия аэростатавыполняются на высоте h =1500м. Тогда, из закона
Архимеда:
,
где mв – масса вытесненного воздуха, mг-масса
гелия.
Решив это уравнение, ответим на вопрос задачи
Выразим mв и mг mв=rвV, где rв = 0,8rвп,
где rвп – плотность
воздуха у поверхности земли.
Тогда
, а .
Следовательно
.
Аналогично .
Тогда
.
Произведем вычисление: M=380кг.
Пример 7. Спутник погрузился в тень
Земли. При этом температура внутри спутника, равная вначале T1=300K,
упала на 1%, вследствие чего давление воздуха изменилось на величину Dp=10,5×102Па.
Определите массу воздуха в спутнике, если его объем V=10м3.
Дано
Решение
T1=300K
DT=0.01
T=3K
Dp=10,5×102Па
V=10м3
m=29×10-3кг/моль
________________
m=?
Считаем, что газ (воздух) внутри спутника является идеальным.
Запишем уравнение Менделеева – Клайперона для каждого состояния:
,(1)
,(2)
(3)
Объем V, масса m, молярная масса m газа являются постоянными. В системе трех уравнений не
известны три величины: m, p1 и р2. Следовательно,
система разрешима.
Так как температура упала, то T1=T2+DT. Вычитая из уравнения (1) уравнение (2),
получаем
.
Но p1–p2=Dp, а T1–T2=DT. Тогда приходим к уравнению:
.
Отсюда: .
Произведем вычисления: m=12кг.
Пример 8. Идеальный газ, масса
которого равна 6,1кг, занимает объем 5м3 при давлении 2∙105Па.
Определите среднюю квадратичную скорость движения молекул газа.
Дано
Решение
m=6,1кг
V=5м3
р=2∙105Па
_____________
<кв>-?
Средняя квадратичная скорость молекулы: . Из уравнения
Менделеева – Клапейрона: найдем: . Тогда .
Произведя вычисления, получим: <кв> = 700м/с
Пример 9. В баллоне находится азот
массой 4г при 300К. Определите среднюю энергию поступательного движения
молекул, находящихся в баллоне.
Дано
Решение
m=4г= 4•10-3кг
Т=300К
μ = 28•10-3кг/моль
________________
<Wn> – ?
Средняя энергия поступательного движения всех молекул определяется
выражением:
; (1)
где <εn> – средняя энергия поступательного
движения одной молекулы; N – число молекул, находящихся в баллоне. Известно,
что ,(2)
где k=1,38•10-23Дж/К – постоянная Больцмана, Т
– термодинамическая температура. Число N молекул найдем по формуле:
, (3)
где n- количество
вещества, NА =6,02•1023моль-1 – постоянная
Авогадро.
Известно, что
,(4)
где m – масса азота, μ = 28•10-3кг/моль –
молярная масса азота.
Выражение (1) с учетом (2), (3) и (4) примет вид:
. (5)
Произведем вычисления по формуле (5), получим:
<Wn>≈534 Дж.
Пример 10. Смесь водорода и гелия
при температуре 27˚C находится под давлением 2∙102Па.
Масса водорода составляет 60% от общей массы смеси. Определите концентрацию
молекул каждого газа.
Дано
Решение
Т=300К
р=2•102Па
k=1,38•10-23Дж/К
τ1=0,6
τ2=0,4
_______________
n1, n2 – ?
Масса каждого из газов определяется из соотношений
, , (1)
где m – масса смеси, τ1 и τ2
– массовые доли соответственно водорода и гелия.
С другой стороны, масса каждого из газов:
, .
(2)
Сравнив (1) и (2), получим:
,
, откуда
. (3)
Для смеси газов
. (4)
Из выражения (3) и (4) получим:
,. (5)
При заданном давлении водород и гелий можно считать идеальными
газами, подчиняющимися уравнению , отсюда (6). С учетом
(6) преобразуем соотношения (5):
, . (7)
Произведем вычисления: n1 ≈ 0,36•1023,
n2 ≈ 0,12•1023.
Пример 11. Определите полную энергию
и количество молекул воздуха между рамами окна, если площадь окна S=2м2,
расстояние между рамами ℓ=0,2м. Давление воздуха между рамами
атмосферное, а температура его линейно изменяется вдоль ℓ от t1=
-10˚C (t1 – температура наружного стекла) до t2=20˚C
(t2–температура внутреннего стекла).
Дано
Решение
S=2м2
ℓ=0,2м
Т1=263K
Т2=293K
________________
W-?
N-?
По условию задачи, воздух между рамами находится в неравновесном
состоянии, так как температура изменяется вдоль оси Оx (Рис.2), ее
распределение в объеме воздуха не изменяется со временем. В пределах
достаточно тонкого слоя толщиной dx, температуру можно считать постоянной и
равной Т. Тогда энергия
.(1)
Концентрации молекул в пределах этого слоя определив из
уравнения состояния:
.(2)
Тогда число dN молекул в объеме слоя:
,(3)
а их энергия
.(4)
По условию задачи температура между рамами изменяется
линейно:
,
(5)
где α – постоянная.
Решая совместно уравнения (2), (3), (5), получим:
.
Тогда
(6)
Постоянные α и Т0 найдем из граничных условий: при
х=0 Т=Т1, следовательно, Т0=Т1; при
х=ℓ, Т= Т2, следовательно,
,
отсюда
.
Тогда
.(7)
Полная энергия dW всех молекул в слое dx:
.
Тогда
.(8)
Произведем вычисления по формулам (7) и (8), учитывая, что
i=5, р=1,01•105Па, N = 1,06•1025, W = 1•105Дж.
Пример 12. Определите среднюю
кинетическую энергию, среднюю энергию вращательного и среднюю энергию
поступательного движения одной молекулы аммиака NH3 при 27˚C.
Дано
Решение
Т=300К
________________
<ε>-?
<εn>-?
<εвр>-?
Средняя полная энергия молекулы:
,(1)
где i – число степеней свободы, k =1,38•10-23Дж/К
– постоянная Больцмана, Т – термодинамическая температура.
Средняя энергия поступательного движения молекулы:
, (2)
где число 3 означает число степеней поступательного движения
молекул. Средняя энергия поступательного движения молекул:
.
Учтя, что молекула аммиака является четырехатомной, т.е.
ее число степеней свободы равно 6, получим:
,
откуда
. (3)
Произведем вычисления по формулам (1) и (3):
<ε>=1,24•10-20Дж; =6,2•10-21Дж.
Пример 13. Определите среднюю
арифметическую скорость молекул идеального газа, плотность которого при
давлении 35кПа составляет 0,3кг/м3.
Дано
Решение
р=35×103Па
ρ=0,3кг/м3
_______________
<υ>-?
Согласно уравнению молекулярно – кинетической теории
идеальных газов
,(1)
где n – концентрация молекул, m0–масса одной
молекулы, <υкв> – средняя квадратичная скорость
молекул.
Учитывая, что , а , получаем:
.(2)
Так как плотность газа , где m – масса газа, V
– его объем, N – число всех молекул газа, то уравнение (1) можно записать в
виде:
или .
Подставляя это выражение в формулу (2), находим искомую
среднюю арифметическую скорость:
.
Вычисляя, получаем: <υ> = 545 м/с.
Пример 14. Используя функцию
распределения молекул идеального газа по относительным скоростям , где , определите число
молекул, скорости которых меньше 0,002 наиболее вероятной скорости, если в
объеме газа содержится N=1,67×1024
молекул.
Дано
Решение
υmax =0,002 υв
N=1,67×1024
_______________
DN-?
Число dN(u) молекул, относительные скорости которых заключены
в пределах от u до u+du
,(1)
где N – число молекул в объеме газа.
По условию задачи, υmax=0,002υв,
то umax= υmax/υв=0,002.
Так как u<1, то e-u² ≈ 1-u2. Пренебрегая
u2<1, выражение (1) можно записать в виде:
.(2)
Проинтегрировав выражение (2) по u в пределах от 0 до umax,
найдем
.
Вычисляя, получаем ∆N=1016 молекул.
Пример 15. Средняя длина
<ℓ> свободного пробега молекулы углекислого газа при нормальных
атмосферных условиях равна 40 нм. Определите среднюю арифметическую скорость
<υ> молекул и среднее число <z> соударений, которые испытывает
молекула в 1 секунду.
Дано
Решение
<ℓ> = 40×10-9м
_______________
<υ>-?, <z>-?
Средняя арифметическая скорость молекул определяется по
формуле:
,(1)
где μ- молярная масса вещества.
Среднее число соударений молекулы в 1 секунду равно отношению
средней скорости <υ> молекулы к средней длине <ℓ> ее
свободного пробега:
.(2)
Произведем вычисления по формулам (1) и (2):
<υ>=362м/с, <z>=9,05·109с-1.
Пример 16. Барометр в кабине
летящего самолета все время показывает одинаковое давление р=79кПа, благодаря
чему летчик считает высоту h1 полета неизменной. Однако температура
воздуха за бортом изменилась с t=5˚C до t=1˚C. Какую ошибку
∆h в определении высоты допустил летчик? Давление р0 у
поверхности Земли считать нормальным.
Дано
Решение
р=79 ×103Па
t1=5˚C,
Т1=278К
t2=1˚C,
Т2=274К
_____________
∆h – ?
Для решения задачи воспользуемся барометрической формулой:
.
Барометр может показывать одинаковое давление р при изменении
температуры за бортом от Т1 до Т2 только в том случае,
если самолет изменяет высоту полета от h1 (которую летчик считает
неизменной), до некоторой другой h2. Запишем барометрическую формулу
для этих двух случаев:
Найдем отношение р0/р и обе части полученного
равенства прологарифмируем:
;
.
Из полученных соотношений выразим высоты h2 и h1
и найдем их разность:
.(1)
Подставим в выражение (1) значения величин (давления в отношении
р0/р можно выразить в килопаскалях, это не повлияет на окончательный
результат): ∆h=-28,5 м. Знак “–“ означает, что h2<h1
и, следовательно, самолет спустился на 28,5 метров по сравнению с предполагаемой высотой.
Пример 17. Определите, во сколько
раз отличаются коэффициенты диффузии азота (μ1=28·10-3кг/моль)
и углекислого газа (μ2=44·10-3кг/моль), если оба
газа находятся при одинаковых температуре и давлении. Эффективные диаметры
молекул этих газов считать одинаковыми.
Дано
Решение
μ1=28·10-3кг/моль
μ2=44·10-3кг/моль
________________
D1/D2-?
Коэффициент диффузии газа
,(1)
где – средняя арифметическая
скорость его молекул, – средняя длина свободного
пробега молекул. Поскольку p=nkT,
из условия задачи (p1=p2, Т1=Т2)
следует, что n1=n2. Подставив значения
<υ>,<ℓ> в формулу (1) и учитывая условие задачи,
найдем Вычисляя, получим D1/D2=1,25.
Источник
