В сосуде под подвижным поршнем который может скользить без трения
12. МКТ и Термодинамика (изменение физических величин в процессах, установление соответствия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
В вертикальном цилиндрическом сосуде под подвижным поршнем массой (M), способным скользить без трения вдоль стенок сосуда, находится идеальный газ. Газу сообщают некоторое количество теплоты. Как в этом процессе изменяются следующие физические величины: концентрация молекул и средняя кинетическая энергия хаотического движения молекул газа?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.твете могут повторяться. [begin{array}{|c|c|c|}
hline
text{ Концентрация молекул газа }
&text{ Средняя кинетическая энергия }\
& text{ хаотического }
text{ движения молекул газа}
\
hline
&\
hline
end{array}]
Концентрация — 2
1) Концентрация молекул: [n=dfrac{N}{V},] где (N) — количество молекул газа в объеме (V).
Объем в данном процессе увеличивается, а количество молекул не меняется. Следовательно, концентрация молекул газа уменьшается.
Средняя кинетическая энергия хаотического движения молекул газа — 1
2) Среднюю кинетическую энергию можно найти по формуле: [E_{k}=dfrac{3}{2}kT,] где (k) — постоянная Больцмана, (T) — абсолютная температура газа.
Так как температура увеличивается, то (E_k) также увеличивается.
Ответ: 21
В цилиндрическом сосуде под поршнем находится газ. Поршень не закреплён и может перемещаться в сосуде без трения (см. рисунок). В сосуд закачивается ещё такое же количество газа при неизменной температуре. Как изменится в результате этого давление газа и концентрация его молекул? 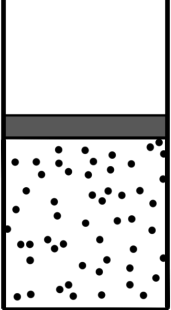
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться. [begin{array}{|c|c|}
hline
text{ Давление газа}&text{ Концентрация молекул}\
hline
&\
hline
end{array}]
Давление — 3
1) Так как поршень подвижный (не закреплен), то процесс будет происходить при постоянном давлении.
Концентрация — 3
2) Давление газа связано с его концентрацией: [p=nkT,] где (k) — постоянная Больцмана, (n) — концентрация молекул газа, (T) — абсолютная температура газа.
Выразим концентрацию газа: [n=dfrac{p}{kT}] Так как давление и температура постоянны, то концентрация не изменится.
Ответ: 33
В сосуде неизменного объема находится идеальный газ. Часть газа выпускали из сосуда так, что давление оставалось неизменным. Как изменились при этом температура газа, оставшегося в сосуде, и его плотность ?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться. [begin{array}{|c|c|c|}
hline
text{ Температура газа} &text{ Плотность газа }\
hline
&\
hline
end{array}]
Температура газа — 1
1)Уравнение состояния газа: [pV=nu RT,] где (p) — давление газа, (V) — объем, занимаемый газом, (nu) — количество вещестав, (R) — универасальная газовая постоянная, (T) — абсолютная температура.
Выразим температуру газа: [T=dfrac{pV}{nu R}] При уменьшении количества газа ((V=const), (p=const)) его температура увеличится.
Плотность — 2
2) Плотность газа: [rho=dfrac{m}{V},] где (m) — масса газа.
Так как объем газа не изменяется, а его масса уменьшается, то плотность газа также уменьшается.
Ответ: 12
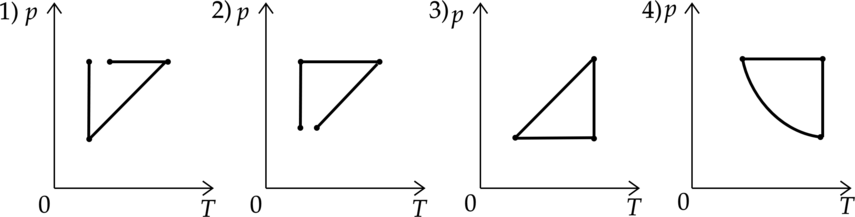
Идеальный газ совершает два процесса. Процесс 1 – газ сначала охлаждался при постоянном давлении, потом его давление уменьшалось при постоянном объеме, затем при постоянной температуре объем газа уменьшался до первоначального значения. Процесс 2 – температура газа уменьшалась при постоянном давлении, потом давление газа увеличивалось при постоянном объеме, а затем температура газа оставалась неизменной при уменьшении давления. Какие из графиков в координатных осях р – T соответствует этим изменениям состояния газа? 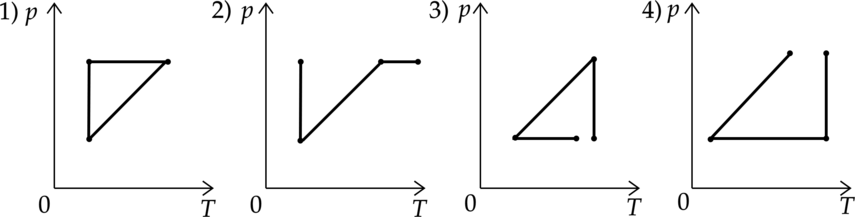
[begin{array}{|c|c|}
hline
text{ПРОЦЕССЫ}&text{ГРАФИКИ}\
hline
1& 1)\
&2)\
hline
2&3)\
&4)\
hline
end{array}]
Распишем, как должны выглядеть процессы в координатах p-T. Процесс 1 – газ сначала охлаждался при постоянном давлении – горизонтальная прямая , потом его давление уменьшалось при постоянном объеме – прямая, проходящая через начало координат, затем при постоянной температуре объем газа уменьшался до первоначального значения – вертикальная прямая. Нам подходит вариант 2, а вариант 3 не подходит так как газ по условию вернулся в первоначальное положение. Процесс 2 – температура газа уменьшалась при постоянном давлении – горизонтальная прямая, потом давление газа увеличивалось при постоянном объеме – прямая, проходящая через начало координат, а затем температура газа оставалась неизменной при уменьшении давления – вертикальная прямая. Нам подходит вариант 3.
Ответ: 23
Идеальный газ совершает два процесса. Процесс 1 – газ сначала нагревался при постоянном давлении, потом его давление уменьшалось при постоянном объеме, затем при постоянной температуре давление газа увеличилось до первоначального значения. Процесс 2 – газ расширяется таким образом, что давление обратно пропорционально температуре, затем давление газа увеличивалось при постоянной температуре, а в конце температура газа уменьшалось при уменьшении объема газа. Какие из графиков в координатных осях р — Т соответствует этим изменениям состояния газа? 
[begin{array}{|c|c|}
hline
text{ПРОЦЕССЫ}&text{ГРАФИКИ}\
hline
1& 1)\
&2)\
hline
2&3)\
&4)\
hline
end{array}]
Распишем, как должны выглядеть процессы в координатах p-T. Процесс 1 – газ сначала нагревался при постоянном давлении – горизонтальная прямая, потом его давление уменьшалось при постоянном объеме – прямая, направленная под углом к осям, затем при постоянной температуре давление газа увеличилось до первоначального значения – вертикальня прямая.График – 1. Процесс 2 – газ расширяется таким образом, что давление обратно пропорционально температуре – гипербола, затем давление газа увеличивалось при постоянной температуре – вертикальная прямая, а в конце температура газа уменьшалось при уменьшении объема газа – горизонтальная прямая. График – 4.
Ответ: 14
В цилиндрическом сосуде под закрепленным поршнем находится газ. Поршень немного выдвигают из сосуда и снова закрепляют. Как при этом изменяется концентрация молекул газа (n) и давление газа (p), если средняя квадратичная скорость движения молекул (overline{v_0}) остается неизменной?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;
2) уменьшилась;
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Концентрация}&text{Давление}\
text{молекул газа}&text{газа}\
hline
& \
hline
end{array}]
Запишем основное уравнение МКТ: [~~~~~~~~~~~~~~~p=dfrac{1}{3}nm_0overline{v_0^2},~~~~~~~(1)] где (m_0) — масса одной молекулы газа. [n=dfrac{N}{V},] где (V) — объем газа.
Значит (nsimdfrac{1}{V}).
По условию объем увеличивается, т.к. поршень выдвигают из сосуда. Значит, концентрация молекул газа уменьшается.
Из (1) получаем, что (psim n), значит давление газа также уменьшается.
Ответ: 22
В сосуде под закрепленным поршнем находится газ. Как изменятся его плотность (rho) и давление (p), если среднюю квадратичную скорость молекул газа (overline{v_0}) увеличить?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;
2) уменьшилась;
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Плотность}&text{Давление}\
text{газа}&text{газа}\
hline
& \
hline
end{array}]
Запишем основное уравнение МКТ: [~~~~~~~~~~~~~~~p=dfrac{1}{3}rhooverline{v_0^2}~~~~~~~(1)] Известно, что (rho=dfrac{m}{V}). В нашем случае (m) и (V) — не изменяющиеся величины, значит (rho=const).
Из (1) получаем, что (psim overline{v_0^2}). Значит, если (overline{v_0}) увеличивается, то и (p) увеличивается.
Ответ: 31
Источник
Задача по физике – 12875
Микропроцессор при работе выделяет значительное количество тепла. На практике удается ускорить работу микропроцессора за счет увеличения так называемой тактовой частоты – но при этом возрастает выделяемая мощность (очень грубо можно считать, что она пропорциональна рабочей частоте микропроцессора). Для уменьшения перегрева на корпус микропроцессора надевают металлический радиатор, имеющий большую поверхность, улучшающую теплообмен с окружающим воздухом. Темпера тура корпуса микропроцессора, работающего е самодельной ЭВМ в обычном режиме, составляет $+95^{ circ} С$, температура радиатора при этом $+50^{ circ} С$, а температура воздуха в корпусе ЭВМ $+30^{ circ} С$. При помощи специальной пасты с высокой теплопроводностью удалось улучшить тепловой контакт корпуса микропроцессора с радиатором – температура микро процессора снизилась при этом до $+65^{ circ} С$. Во сколько раз можно теперь повысить быстродействие микро процессора, если предельно допустимая температура его корпуса составляет $+95^{ circ} С$? Температуру внутри корпуса можно считать неизменной, для оценки можно также считать что условия теплообмена остаются прежними.
Подробнее
Задача по физике – 12876
Порцию кислорода нагревают при постоянном давлении до тех пор, пока объем газа не возрастет в 2 раза, а затем охлаждают, при получившемся объеме пока газ не отдаст все тепло полученное при расширении. Найдите отношение начальной и конечной температур в этом процессе.
Подробнее
Задача по физике – 12882
В вертикальном сосуде под тяжелым поршнем находится некоторое количество двухатомного газа. Сосуд обладает хорошей теплопроводностью, температура окружающей среды $T_{0}$ постоянна. При этой температуре происходит необратимая диссоциация молекул газа, причем энергия взаимодействия атомов в молекуле составляет $epsilon$ в расчете на один моль. Какое количество теплоты получит газ от окружающей среды за большой интервал времени? Начальные значения давления и объема составляют $p_{0}$ и $V_{0}$ соответственно.
Подробнее
Задача по физике – 12889
В длинной горизонтальной гладкой пустой трубе находятся два поршня, которые могут скользить без трения вдоль трубы. Один из поршней имеет массу $M = 1 кг$, другой – в два раза тяжелее. В начальный момент между поршнями находится моль кислорода при температуре $T = 300 К$, а тяжелый поршень движется со скоростью $v_{0} = 1 м/с$ по на правлению к неподвижному в этот момент легкому поршню. Чему равна максимальная температура газа в этом процессе? Найдите также скорости поршней через большой отрезок времени. Теплоемкость стенок трубы и поршней считать малой, теплопроводностью пренебречь.
Подробнее
Задача по физике – 12896
В вертикальном сосуде под тяжелым поршнем находится небольшое количество гелия. Атмосферное давление отсутствует, поршень “высот” над дном сосуда на высоте $H$. Поршень очень быстро поднимают на высоту $10H$ относительно дна сосуда и отпускает. На какой высоте над дном сосуда он установится после того, как его колебания затухнут? Сосуд теплонепроницаемый, теплоемкостью стенок и поршня можно пренебречь. Трение поршня о стенки пренебрежимо мало. Несколько лишних для этой задачи данных: масса поршня $M$, ускорение свободного падения $g$, площадь дна сосуда $S$. Что понимать в условии под выражением “очень быстро Как изменится ответ, если поднимать поршень очень медленно?
Подробнее
Задача по физике – 12903
Сосуд объемом 5 литров с жесткими стеклянными стенками соединен короткой жесткой трубкой с горлышком литровой пластиковой бутылки из-под газированной воды – ее тонкие стенки практически нерастяжимые, но довольно мягкие. В системе из двух сосудов находится неизменное количество воздуха. Воздух понемногу охлаждают, измеряя его давление. Вплоть до температуры $+50^{ circ} С$ давление в системе уменьшалось, а начиная с этой температуры перестало уменьшаться. При какой температуре давление снова начнет уменьшатся? Атмосферное давление остается постоянным.
Подробнее
Задача по физике – 12909
В невесомости проводится следующий опыт. Заполненный воздухом большой сосуд содержит множество мельчайших масляных капелек и одну каплю довольно больших размеров. При столкновении маленьких капель между собой они упруго разлетаются, а при столкновении с большой каплей происходит их поглощение. За 1 час диаметр большой капли увеличился в 2 раза. Через какое время он увеличится еще в 2 раза? Большая капля не касается стенок сосуда. Испарения с ее поверхности не происходит.
Подробнее
Задача по физике – 12911
В вертикальном теплоизолированном сосуде под массивный подвижным поршнем находится порция идеального одноатомного газа при температуре $T_{0}$, поршень при этом находится в равновесии. Температуру газа в сосуде при помощи миниатюрного нагревателя очень быстро увеличивают в 2 раза и оставляют систему в покое. Какая температура установится в сосуде после того, как поршень перестанет двигаться? Трение поршня о стенки пренебрежимо мало. Поршень и стенки практически не получают тепла от газа. Воздуха снаружи нет.
Подробнее
Задача по физике – 12912
Теплопроводность дерева вдоль волокон в 2 раза больше, чем поперек. Два длинных тонких цилиндра одинаковых размеров сделаны из такого дерева; ось одного из них направлена вдоль волокон, ось другого составляет с направлением волокон угол $30^{ circ}$. Боковые поверхности цилиндров теплоизолируют и создают одинаковые разности температур между торцами цилиндров. Во сколько раз отличаются тепловые потоки в этих цилиндрах?
Подробнее
Задача по физике – 12918
В кубическом сосуде объемом $V = 1 м^{3}$ находится гелий при температуре $T = 300 К$ и давлении $p = 10^{5} Па$. В стенке сосуде открывают отверстие площадью $S = 1 см^{2}$ и через время $tau = 0,01 с$ закрывают. Снаружи – вакуум. Оцените изменение температуры газа в сосуде после установления в нем равновесия. Считайте, что открывание и закрывание отверстие производят очень аккуратно – не создавая лишних потоков газа.
Подробнее
Задача по физике – 12921
Горизонтально расположенный цилиндрический сосуд с массивным поршнем находится в вакууме (рис.). Пружина жесткостью $k$, закрепленная с одной стороны, упирается в поршень. В начальном положении газа под поршнем нет, пружина не деформирована. Через дырку в дне сосуда в него впускают некоторое количество гелия и закрывают дырку. После установления равновесия пружина оказалась деформированной на $L$. Затем газ очень медленно нагревают, пока поршень не сдвигается еще на $L$. Какое количество теплоты получил газ при этом? Теплоемкостью стенок и поршня пренебречь.

Подробнее
Задача по физике – 12928
Моль гелия в процессе расширения получает тепло, его теплоемкость при этом составляет $C = 15 Дж/(моль cdot К)$. Найдите изменение температуры газа в этом процессе при совершении им работы $A = 20 Дж$.
Подробнее
Задача по физике – 12935
В вертикальном теплоизолированном сосуде под тяжелым поршнем находится порция азота. На поршне сверху лежит груда песка, система находится в равновесии, начальный объем газа $V_{1}$, начальное давление $p_{1}$. Начнем медленно, по одной песчинке, убирать песок и уменьшим давление до $p_{2}$; при этом объем газа увеличится до $V_{2}$ (конечно, можно было этот объем вычислить, но будем считать, что это уже сделали и вам сообщили результат). Теперь проведем эксперимент иначе – снимем всю порцию песка сразу. Какую кинетическую энергию имел бы в этом случае поршень в тот момент, когда объем газа составил бы $V_{2}$? Считайте газ достаточно разреженным.
Подробнее
Задача по физике – 12942
Комната площадью $S = 20 м^{2}$ с высотой потолка $H = 3 м$ заполнена воздухом при нормальных условиях. Оцените число ударов молекул о потолок за время $tau = 1 ч$. Куда чаще ударяют молекулы – в пол или в потолок комнаты? Оцените разность чисел ударов молекул о пол и о потолок за время $tau$. Считайте температуру воздуха в комнате повсюду одинаковой.
Подробнее
Задача по физике – 12947
Для снабжения небольшою дома горячей водой применено не самое удачное устройство. Оно состоит из очень большого бака с теплоизоляцией, от которого потребители получают маленькими порциями горячую воду, и автоматического устройства, которое сразу же пополняет бак крутым кипятком. Оказалось, что при стандартном количестве потребляемой воды температура воды в баке составляет $+60^{ circ} С$ при температуре окружающего воздуха $+20^{ circ} С$. Какая температура установится в баке при увеличении расхода воды вдвое? Теплоотдача в окружающую среду пропорциональна разности температур.
Подробнее
Источник
