В сосуде под поршнем находится идеальный газ массой
5.4. Практическое применение уравнения состояния идеального газа
5.4.3. Уравнение состояния для газа, находящегося в сосуде под поршнем
Для идеального газа, находящегося в сосуде под поршнем, необходимо учитывать следующее:
- масса газа, находящегося в сосуде под поршнем, вследствие изменения термодинамических параметров газа не изменяется:
m = const;
- постоянным остается также количество вещества (газа):
ν = const;
- плотность газа и концентрация его молекул (атомов) изменяются:
ρ ≠ const, n ≠ const.
Пусть изменение состояния идеального газа, находящегося в цилиндрическом сосуде под поршнем, вызвано действием на поршень внешней силы F→ (рис. 5.9).
Рис. 5.9
Начальное и конечное состояния газа в сосуде под поршнем описываются следующими уравнениями:
p1V1=νRT1,p2V2=νRT2,}
где p
1, V
1, T
1 — давление, объем и температура газа в начальном состоянии; p
2, V
2, T
2 — давление, объем и температура газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).
Условия равновесия поршня, закрывающего идеальный газ в сосуде (см. рис. 5.9), в начале процесса и в конце процесса выглядят следующим образом:
Mg+FA=F1,Mg+FA+F=F2,}
где M — масса поршня; g — модуль ускорения свободного падения; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление; S — площадь сечения поршня; F
1 — модуль силы давления газа на поршень в начале процесса, F
1 = p
1S; p
1 — давление газа в сосуде в начальном состоянии; F — модуль силы, вызывающей сжатие газа; F
2 — модуль силы давления газа на поршень в конце процесса, F
2 = p
2S; p
2 — давление газа в сосуде в конечном состоянии.
Температура идеального газа, находящегося в сосуде под поршнем, может как изменяться, так и оставаться неизменной:
- если процесс движения поршня происходит достаточно быстро, то температура газа изменяется —
T ≠ const;
- если процесс происходит медленно, то температура газа остается постоянной –
T = const.
Давление идеального газа, находящегося в сосуде под поршнем, также может изменяться или оставаться неизменным:
- если в задаче сказано, что поршень является легкоподвижным, то давление газа под поршнем — неизменно (в том случае, когда из условия задачи не следует обратное) — p = const;
- в остальных случаях давление газа под поршнем изменяется — p ≠ const.
Масса поршня, закрывающего газ в сосуде, либо равна нулю, либо имеет отличное от нуля значение:
- если в задаче сказано, что поршень является легким или невесомым, то масса поршня считается равной нулю —
M = 0;
- в остальных случаях поршень обладает определенной ненулевой массой —
M ≠ const.
Пример 19. В вертикальном цилиндре под легкоподвижным поршнем сечением 250 мм2 и массой 1,80 кг находится 360 см3 газа. Атмосферное давление равно 100 кПа. На поршень поставили гири, и он сжал газ до объема 240 см3. Температура газа при его сжатии не изменяется. Определить массу гирь.
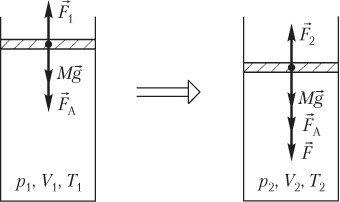
Решение. На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня Mg→;
- сила атмосферного давления F→A;
- сила давления газа F→1, действующая со стороны газа (до его сжатия);
- сила давления газа F→2, действующая со стороны газа (после его сжатия);
- mg→ — вес гирь.
Условие равновесия поршня запишем в следующем виде:
- до сжатия газа —
F
1 = Mg + F
A,
где F
1 — модуль силы давления газа, F
1 = p
1S; p
1 — давление газа до сжатия; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление; g — модуль ускорения свободного падения;
- после сжатия газа —
F
2 = Mg + F
A
+ mg,
где F
2 — модуль силы давления газа, F
2 = p
2S; p
2 — давление газа после сжатия; mg — вес гирь; m — масса гирь.
Считая процесс сжатия газа изотермическим, запишем уравнение Менделеева — Клапейрона для газа под поршнем следующим образом:
- до его сжатия —
p
1V
1 = νRT,
где V
1 — первоначальный объем газа под поршнем; ν — количество газа под поршнем; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа (не изменяется в ходе процесса);
- после его сжатия —
p
2V
2 = νRT,
где V
2 — объем сжатого поршнем газа.
Равенство
p
1V
1 = p
2V
2
и два условия равновесия, записанные в явном виде, образуют полную систему уравнений:
p1S=Mg+pAS,p2S=Mg+pAS+mg,p1V1=p2V2,}
которую требуется решить относительно массы гирь m.
Для этого выразим отношение давлений p
2/p
1 из первой пары уравнений:
p2p1=Mg+pAS+mgMg+pAS
и из третьего уравнения:
p2p1=V1V2,
запишем равенство правых частей полученных отношений:
Mg+pAS+mgMg+pAS=V1V2.
Отсюда следует, что искомая масса определяется формулой
m=(M+pASg)(V1V2−1).
Вычисление дает результат:
m=(1,80+100⋅103⋅250⋅10−610)(360⋅10−6240⋅10−6−1)=2,15 кг.
Указанное сжатие газа вызвано гирями массой 2,15 кг.
Пример 20. Открытый цилиндрический сосуд сечением 10 см2 плотно прикрывают пластиной массой 1,2 кг. Атмосферное давление составляет 100 кПа, а температура окружающего воздуха равна 300 К. На сколько градусов нужно нагреть воздух в сосуде, чтобы он приподнял пластину?
Решение. На рисунке показаны силы, действующие на пластину после нагревания газа:
- сила тяжести пластины Mg→;
- сила атмосферного давления F→A;
- сила давления газа F→2, действующая на пластину со стороны нагретого газа.
Пластина находится в состоянии неустойчивого равновесия; условие равновесия пластины выглядит следующим образом:
F
2 = Mg + F
A,
где F
2 — модуль силы давления нагретого газа, F
2 = p
2S; p
2 — давление нагретого газа; S — площадь сечения сосуда; Mg — модуль силы тяжести пластины; M — масса пластины; g — модуль ускорения свободного падения; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление.
Запишем уравнение Менделеева — Клапейрона следующим образом:
- для газа в сосуде до его нагревания
p
1V = νRT
1,
где p
1 — давление газа в сосуде до нагревания (совпадает с атмосферным давлением), p
1 = p
A; V — объем газа в сосуде; ν — количество вещества (газа) в сосуде; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T
1 — температура газа в сосуде до нагревания (совпадает с температурой окружающей среды);
- для газа в сосуде после его нагревания
p
2V = νRT
2,
где p
2 — давление нагретого газа; T
2 — температура нагретого газа.
Два уравнения состояния газа (до и после нагревания) и условие равновесия пластины, записанные в явном виде, образуют полную систему уравнений:
pAV=νRT1,p2V=νRT2,p2S=Mg+pAS;}
систему необходимо решить относительно температуры T
2, до которой следует нагреть газ.
Для этого делением первой пары уравнений
pAVp2V=νRT1νRT2
получим выражение для давления нагретого газа:
p2=pAT2T1
и подставим его в третье уравнение системы:
pAT2ST1=Mg+pAS.
Преобразуем полученное выражение к виду
T2=T1(Mg+pAS)pAS=T1(MgpAS+1),
а затем найдем разность
ΔT=T2−T1=MgT1pAS.
Произведем вычисление:
ΔT=1,2⋅10⋅300100⋅103⋅10⋅10−4=36 К=36 °С.
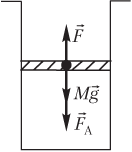
Пример 21. В цилиндрическом сосуде поршень массой 75,0 кг и площадью сечения 50,0 см2 начинает двигаться вверх. Давление газа под поршнем постоянно и равно 450 кПа, атмосферное давление составляет 100 кПа. Считая, что поршень движется без трения, определить модуль скорости поршня после прохождения им 3,75 м пути.
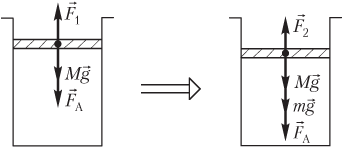
Решение. На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня Mg→;
- сила атмосферного давления F→A;
- сила давления газа F→, действующая на поршень со стороны нагретого газа.
Под действием указанных сил, направленных вверх, поршень движется с ускорением a→:
F→+F→A+Mg→=ma→,
или в проекции на вертикальную ось —
F − F
A − Mg = Ma,
где F — модуль силы давления газа под поршнем, F = pS; p — давление газа; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; g — модуль ускорения свободного падения; a — модуль ускорения поршня.
Преобразуем записанное уравнение, выразив модуль ускорения и выполнив подстановку выражений для модулей сил:
a=F−FA−MgM=(p−pA)SM−g.
Скорость поршня, его ускорение и пройденный путь связаны между собой соотношением
l=v22a,
где l — пройденный путь; v — модуль скорости поршня.
Выразим отсюда модуль скорости поршня:
v=2al
и подставим в записанную формулу выражение для модуля ускорения:
v=2l((p−pA)SM−g).
Выполним расчет:
v=2⋅3,75((450−100)⋅103⋅50⋅10−475,0−10)≈10 м/с.
После прохождения 3,75 м пути поршень приобретет скорость, приблизительно равную 10 м/с.
Источник
| » Кнопка сайта |
| Термодинамика |
А23. Идеальный одноатомный газ находится в закрытом сосуде объёмом 0,6 м3. При охлаждении его внутренняя энергия уменьшилась на 1,8 кДж. В результате давление газа снизилось на |
|
|
|
С1-3. В цилиндре, закрытом подвижным поршнем, находится газ, который может просачиваться сквозь зазор вокруг поршня. В опыте по изотермическому сжатию газа его объем уменьшился вдвое, а давление газа упало в 3 раза. Во сколько раз изменилась внутренняя энергия газа в цилиндре? (Газ считать идеальным.) |
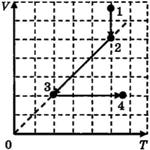
С1-4. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения. |
|
C1-6. В цилиндрическом сосуде под поршнем длительное время находятся вода и ее пар. Поршень начинают выдвигать из сосуда. При этом температура воды и пара остается неизменной. Как будет меняться при этом масса жидкости в сосуде? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения. |
C3-7.Идеальный одноатомный газ находится в сосуде объемом 1,2 м3 под давлением 4•103 Па. Определите внутреннюю энергию этого газа. Ответ выразите в килоджоулях (кДж). |
C3-8.Идеальный одноатомный газ находится в сосуде с жесткими стенками объемом 0,6 м3. При нагревании его внутренняя энергия увеличилась на 18 кДж. Насколько возросло давление газа? Ответ выразите в килопаскалях (кПа). |
С3-9. Нагреваемый при постоянном давлении идеальный одноатомный газ совершил работу 400 Дж. Какое количество теплоты было передано газу? |
С3-10. При изобарном нагревании газообразный гелий получил количество теплоты 100 Дж. Каково изменение внутренней энергии гелия? Масса гелия в данном процессе не менялась. |
С3-11. В сосуде с небольшой трещиной находится воздух. Воздух может медленно просачиваться сквозь трещину. Во время опыта объем сосуда уменьшили в 8 раз, давление воздуха в сосуде увеличилось в 2 раза, а его абсолютная температура увеличилась в 1,5 раза. Каково изменение внутренней энергии воздуха в сосуде? (Воздух считать идеальным газом.) |
С3-12. В сосуде с небольшой трещиной находится воздух. Воздух может медленно просачиваться сквозь трещину. Во время опыта объем сосуда уменьшили в 4 раза, давление воздуха в сосуде увеличилось тоже в 4 раза, а его абсолютная температура увеличилась в 1,5 раза. Каково изменение внутренней энергии воздуха в сосуде? (Воздух считать идеальным газом.) |
С3-13. С разреженным азотом, который находится в сосуде под поршнем, провели два опыта. В первом опыте газу сообщили, закрепив поршень, количество теплоты Q1 = 742 Дж, в результате чего его температура изменилась на некоторую величину ΔT. Во втором опыте, предоставив азоту возможность изобарно расширяться, сообщили ему количество теплоты Q2 = 1039 Дж, в результате чего его температура изменилась также на ΔT. Каким было изменение температуры ΔT в опытах? Масса азота m = 1 кг. |
С3-14. С разреженным азотом, который находится в сосуде под поршнем, провели два опыта. В первом опыте газу сообщили, закрепив поршень, количество теплоты Q1 = 742 Дж, в результате чего его температура изменилась на 1 К. Во втором опыте, предоставив азоту возможность изобарно расширяться, сообщили ему количество теплоты Q2 = 1039 Дж, в результате чего его температура изменилась также на 1 К. Определите массу азота в опытах. |
С3-15. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное давление p = 4 • 105 Па. Расстояние от дна сосуда до поршня L = 30 см. Площадь поперечного сечения поршня S = 25 см2. В результате медленного нагревания газа поршень сдвинулся на расстояние х = 10 см. При движении поршня на него со стороны стенок сосуда действует сила трения величиной Fтр = 3•103 H. Какое количество теплоты получил газ в этом процессе? Считать, что сосуд находится в вакууме. |
С3-16. В горизонтальном цилиндрическом сосуде, закрытом подвижным поршнем, находится одноатомный идеальный газ. Давление окружающего воздуха р = 105 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. В процессе медленного охлаждения от газа отведено количество теплоты │Q│ = 75 Дж. При этом поршень передвинулся на расстояние х = 10 см. Чему равна площадь поперечного сечения поршня? Количество вещества газа постоянно. |
С3-17. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное давление газа р1 = 4·105 Па. Расстояние от дна сосуда до поршня равно L. Площадь поперечного сечения поршня S = 25 см2. В результате медленного нагревания газ получил количество теплоты Q = 1,65 кДж, а поршень сдвинулся на расстояние х = 10 см. При движении поршня на него со стороны стенок сосуда действует сила трения величиной Fтp = 3·103 Н. Найдите L. Считать, что сосуд находится в вакууме. |
|
|
С3-20. Теплоизолированный сосуд объемом V = 2 м3 разделен теплоизолирующей перегородкой на две равные части. В одной части сосуда находится 2 моль Не, а в другой — такое же количество моль Аr. Температура гелия Т1 = 300 К, а температура аргона Т2 = 600 К. Определите парциальное давление аргона в сосуде после удаления перегородки. |

С3-21. На рисунке изображено изменение состояния 1 моль идеального одноатомного газа. Начальная температура газа 27° С. Какое количество теплоты сообщено газу в этом процессе?
 С3-22. На рисунке изображено изменение состояния 1 моль неона. Начальная температура газа 0°С. Какое количество теплоты сообщено газу в этом процессе?
С3-22. На рисунке изображено изменение состояния 1 моль неона. Начальная температура газа 0°С. Какое количество теплоты сообщено газу в этом процессе?
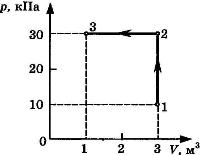 С3-23. На диаграмме представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
С3-23. На диаграмме представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
 С3-24. На диаграмме представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
С3-24. На диаграмме представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
 С3-25. На диаграмме (см. рисунок) представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
С3-25. На диаграмме (см. рисунок) представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?
С3-26. Одноатомный идеальный газ неизменной массы совершает циклический процесс, показанный на рисунке. За цикл от нагревателя газ получает количество теплоты Qн = 8 кДж. Чему равна работа газа за цикл?
 С3-27. С одноатомным идеальном газом неизменной массы происходит циклический процесс, показанный на рисунке. За цикл газ совершает работу Aц = 5 кДж. Какое количество теплоты газ получает за цикл от нагревателя?
С3-27. С одноатомным идеальном газом неизменной массы происходит циклический процесс, показанный на рисунке. За цикл газ совершает работу Aц = 5 кДж. Какое количество теплоты газ получает за цикл от нагревателя?
С3-28. С разреженным азотом, который находится в сосуде с поршнем, провели два опыта. В первом опыте газу сообщили, закрепив поршень, количество теплоты Q1 = 742 Дж, в результате чего его температура изменилась на некоторую величину ΔТ. Во втором опыте, предоставив азоту возможность изобарно расширяться, сообщили ему количество теплоты Q2 = 1039 Дж, в результате чего его температура изменилась также на ΔТ. Каким было изменение температуры ΔТ в опытах? Масса азота m = 1 кг.
С3-29. Один моль аргона, находящийся в цилиндре при температуре T1 = 600 К и давлении p1 = 4•105 Па, расширяется и одновременно охлаждается так, что его давление при расширении обратно пропорционально квадрату объёма. Конечный объём газа вдвое больше начального. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A = 2493 Дж?
С3-30. Один моль аргона, находящийся в цилиндре при температуре T1 = 600 К и давлении p1 = 4•105 Па, расширяется и одновременно охлаждается так, что его давление при расширении обратно пропорционально квадрату объёма. Конечное давление газа p2 = 105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A = 2493 Дж?
С3-31. Один моль одноатомного идеального газа переводят из состояния 1 в состояние 2 таким образом, что в ходе процесса давление газа возрастает прямо пропорционально его объёму. В результате плотность газа уменьшается в α = 2 раза. Газ в ходе процесса получает количество теплоты Q = 20 кДж. Какова температура газа в состоянии 1?
С3-32. Один моль аргона, находящийся в цилиндре при температуре T1 = 600 К и давлении p1 =4•105 Па, расширяется и одновременно охлаждается так, что его давление при расширении обратно пропорционально квадрату объёма. Конечное давление газа р2 = 105 Па. Какую работу совершил газ при расширении, если он отдал холодильнику количество теплоты Q = 1247 Дж?
С3-33. В сосуде объёмом V = 0,02 м3 с жёсткими стенками находится одноатомный газ при атмосферном давлении. В крышке сосуда имеется отверстие площадью s, заткнутое пробкой. Максимальная сила трения покоя F пробки о края отверстия равна 100 Н. Пробка выскакивает, если газу передать количество теплоты не менее 15 кДж. Определите значение s, полагая газ идеальным.
 С3-34. Над одноатомным идеальным газом проводится циклический процесс, показанный на рисунке. На участке 1–2 газ совершает работу А12 = 1000 Дж. На адиабате 3–1 внешние силы сжимают газ, совершая работу |A31| = 370 Дж. Количество вещества газа в ходе процесса не меняется. Найдите количество теплоты |Qхол|, отданное газом за цикл холодильнику.
С3-34. Над одноатомным идеальным газом проводится циклический процесс, показанный на рисунке. На участке 1–2 газ совершает работу А12 = 1000 Дж. На адиабате 3–1 внешние силы сжимают газ, совершая работу |A31| = 370 Дж. Количество вещества газа в ходе процесса не меняется. Найдите количество теплоты |Qхол|, отданное газом за цикл холодильнику.
| » Вход на сайт |
| » Статистика сайта |
| » Календарь | ||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||
| » Подготовка к ЕГЭ |
| » Физика. ЕГЭ |
Источник

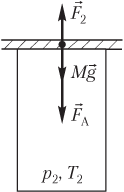
 С1-1. На полу неподвижного лифта стоит теплоизолированный сосуд, открытый сверху. В сосуде под тяжёлым подвижным поршнем находится одноатомный идеальный газ. Поршень находится в равновесии. Лифт начинает равноускоренно опускаться вниз. Опираясь на законы механики и молекулярной физики, объясните, куда сдвинется поршень относительно сосуда после начала движения лифта и как при этом изменится температура газа в сосуде. Трением между поршнем и стенками сосуда, а также утечкой газа из сосуда пренебречь.
С1-1. На полу неподвижного лифта стоит теплоизолированный сосуд, открытый сверху. В сосуде под тяжёлым подвижным поршнем находится одноатомный идеальный газ. Поршень находится в равновесии. Лифт начинает равноускоренно опускаться вниз. Опираясь на законы механики и молекулярной физики, объясните, куда сдвинется поршень относительно сосуда после начала движения лифта и как при этом изменится температура газа в сосуде. Трением между поршнем и стенками сосуда, а также утечкой газа из сосуда пренебречь. С1-2. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения.
С1-2. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения.  С1-2. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения.
С1-2. В цилиндре, закрытом подвижным поршнем, находится идеальный газ. На рисунке показана диаграмма, иллюстрирующая изменение внутренней энергии U газа и передаваемое ему количество теплоты Q. Опишите изменение объема газа при его переходе из состояния 1 в состояние 2, а затем в состояние 3. Свой ответ обоснуйте, указав, какие физические закономерности вы использовали для объяснения. 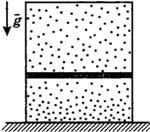 С3-18.Вертикальный замкнутый цилиндрический сосуд высотой 50 см разделен подвижным поршнем весом 110 Н на две части, в каждой из которых содержится одинаковое количество идеального газа при температуре 361 К. Сколько молей газа находится в каждой части цилиндра, если поршень находится на высоте 20 см от дна сосуда? Толщиной поршня пренебречь.
С3-18.Вертикальный замкнутый цилиндрический сосуд высотой 50 см разделен подвижным поршнем весом 110 Н на две части, в каждой из которых содержится одинаковое количество идеального газа при температуре 361 К. Сколько молей газа находится в каждой части цилиндра, если поршень находится на высоте 20 см от дна сосуда? Толщиной поршня пренебречь.  С3-19.В вертикальном теплоизолированном цилиндрическом сосуде под поршнем находится 0,5 моль гелия, нагретого до некоторой температуры. Поршень сначала удерживают, затем отпускают, и он начинает подниматься. Масса поршня 1 кг. Какую скорость приобретет поршень к моменту, когда поршень поднимется на 4 см, а гелий охладится на 20 К? Трением и теплообменом с поршнем пренебречь.
С3-19.В вертикальном теплоизолированном цилиндрическом сосуде под поршнем находится 0,5 моль гелия, нагретого до некоторой температуры. Поршень сначала удерживают, затем отпускают, и он начинает подниматься. Масса поршня 1 кг. Какую скорость приобретет поршень к моменту, когда поршень поднимется на 4 см, а гелий охладится на 20 К? Трением и теплообменом с поршнем пренебречь.