В сосуде под поршнем находится идеальный газ в количестве моль
11. МКТ и Термодинамика (объяснение явлений)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
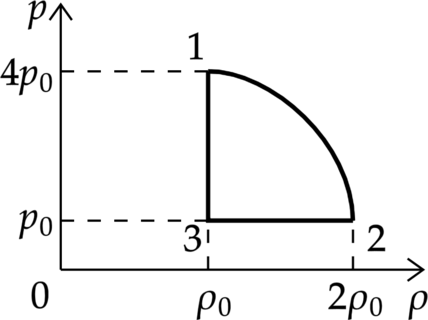
На рисунке показана зависимость давления газа (p) от его плотности (rho) в циклическом процессе, совершаемом 2 моль идеального газа в идеальном тепловом двигателе. Цикл состоит из двух отрезков прямых и четверти окружности.

На основании анализа этого циклического процесса выберите два верных утверждения.
1) В процессе 1−2 температура газа уменьшается.
2) В состоянии 3 температура газа максимальна.
3) В процессе 2−3 объём газа уменьшается.
4) Отношение максимальной температуры к минимальной температуре в цикле равно 8.
5) Работа газа в процессе 3−1 положительна.
“Демоверсия 2017”
1) По уравнению Клапейрона – Менделеева: [p=dfrac{rho}{mu}RT,] где (T) – температура, (mu) – молярная масса газа.
Давление уменьшилось в 4 раза, а плотность увеличилась в 2 раза, следовательно, температура уменьшилась в 8 раз.
Утверждение 1 – (color{green}{small text{Верно}})
2) Аналогично предыдущему пункту [p=dfrac{rho}{mu}RT] Максимальная температура будет в состоянии 1 (давление максимально, плотность минимальна)
Утверждение 2 – (color{red}{small text{Неверно}})
3) В процессе 2 – 3 плотность меньшается, а по формуле: [rho =dfrac{m}{V}] Объем увеличивается
Утверждение 3 – (color{red}{small text{Неверно}})
4) Аналогично пункту 2, минимальность температуры будет достигнута в точке с наименьшим давлением и наибольшей плотностью (т. 2), а отношение температур действительно равно 8
Утверждение 4 – (color{green}{small text{Верно}})
5) В процессе 2 – 3 плотность постоянна, следовательно, объем постоянен и газ не совершает работу.
Утверждение 5 – (color{red}{small text{Неверно}})
Ответ: 14
Сосуд разделён на две равные по объёму части пористой неподвижной перегородкой. В начальный момент времени в левой части сосуда содержится 4 моль гелия, в правой – 40 г аргона. Перегородка может пропускать молекулы гелия и является непроницаемой для молекул аргона. Температура газов одинаковая и остаётся постоянной. Выберите два верных утверждения, описывающих состояние газов после установления равновесия в системе.
1) Концентрация гелия в правой части сосуда в 2 раза меньше, чем аргона.
2) Отношение давления газов в правой части сосуда к давлению газа в левой части равно 1,5.
3) В правой части сосуда общее число молекул газов меньше, чем в левой части.
4) Внутренняя энергия гелия и аргона одинакова.
5) В результате установления равновесия давление в правой части сосуда увеличилось в 3 раза.
“Демоверсия 2020”
Перегородка проницаема только для молекул гелия, поэтому в результате установления равновесия парциальное давление гелия в левой части будет равно парциальному давлению гелия в правой части. Давление газа можно вычислить по формуле: [p=dfrac{nu R T}{V}] Парциальные давления гелия в левой и правой части одинаковы, одинаковы температуры и объёмы частей, следовательно, одинаковы и количества вещества гелия в левой и правой частях сосуда, то есть в левой и правой части сосуда будет содержаться по 2 моля гелия.
Найдём связь концентрации и количества вещества: [n=dfrac{N}{V}=dfrac{nu N_A}{V}] То есть концентрации и количества вещества зависят прямо пропорционально друг от друга, также заметим, что чем больше количество вещества, тем больше и количество молекул.
Найдём количество вещества аргона: [nu_{Ar}=dfrac{m_{Ar}}{mu_{Ar}}=dfrac{40text{ г}}{40text{ г/моль}}=1text{ моль}]
Используя полученное выше, рассмотрим данные в задании утверждения.
Концентрация гелия в два раза больше концентрации аргона в правой части сосуда
1) (color{red}{small text{Неверно}})
Концентрация гелия в два раза больше концентрации аргона в правой части сосуда
2) (color{green}{small text{Верно}})
Отношение давлений: [dfrac{p_text{ п}}{p_text{ л}}=dfrac{nu_text{ г.п}+nu_{Ar}}{nu_text{ г.л}}=dfrac{2text{ моль}+1text{ моль}}{2text{ моль}}=1,5] Где (nu_{text{ г.п.}},nu_{text{ г.л.}}) – количество вещества гелия в правой части, количество вещества гелия в левой части соответственно.
3) (color{red}{small text{Неверно}})
Количество вещества газов в правой части сосуда больше количества вещества газа в левой части сосуда, следовательно, в правой части сосуда общее число молекул газа больше, чем в левой части сосуда.
4) (color{red}{small text{Неверно}})
Внутренняя энергия одноатомного идеального газа может быть вычислена по формуле: [U=dfrac{3}{2}nu R T] Температура газов одинакова. Количество вещества гелия больше количества вещества аргона, следовательно, внутренняя энергия гелия больше внутренней энергии аргона.
5) (color{green}{small text{Верно}})
айдём отношение конечного давления в правой части сосуда к начальному давлению в правой части сосуда: [dfrac{p_{k}}{p_text{ н}}=dfrac{nu_{text{ г.п.}}+nu_{Ar}}{nu_{Ar}}=dfrac{2text{ моль}+1text{ моль}}{1text{ моль}}=3]
Ответ: 25
В цилиндрическом сосуде под поршнем находится газ. Поршень может перемещаться в сосуде без трения. На дне сосуда лежит стальной шарик (см. рисунок). Газ нагревают.
Выберите из предложенного перечня два верных утверждения, верно описывающие данный процесс, и укажите их номера.
1) Объём газа в этом процессе остаётся неизменным.
2) Давление газа в сосуде остаётся неизменным.
3) Плотность газа в этом процессе увеличивается.
4) Сила Архимеда, действующая на шарик, уменьшается.
5) Концентрация молекул газа в сосуде увеличивается.
1) Так как поршень подвижный (не закреплен), то процесс будет происходить при постоянном давлениии.
Уравнение состояния газа: [pV=nu RT] где (nu) — количество вещества, (T) — температура в Кельвинах, (p) — давление газа, (V) — объем, занимаемый газом, (R) — универсальная газовая постоянная. Выразим объем [V=dfrac{nu RT}{p}] При нагревании газа объем увеличивается.
Утверждение 1 — (color{red}{smalltext{Неверно }})
2) Утверждение 2 — (color{green}{smalltext{Верно }})
3) Плотность газа: [rho=dfrac{m}{V}] При нагревании объем увеличивается, значит плотность уменьшается.
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) Сила Архимеда: [F_{text{Арх}}=rho gV] где (rho) — плотность газа, (V) — объем шарика, (g) — ускорение свободного падения. Плотность уменьшается, значит, сила Архимеда уменьшается.
Утверждение 4 — (color{green}{smalltext{Верно }})
5) Концентрация: [n=dfrac{N}{V}] При нагревании газа объем увеличивается, концентрация уменьшается.
Утверждение 5 — (color{red}{smalltext{Неверно }})
Ответ: 24
На (pV)—диаграмме отображена последовательность трёх процессов (1 — 2 — 3) изменения состояния 2 моль идеального газа. 
Из предложенного перечня утверждений выберите два правильных и укажите их номера.
1) В процессе 1 газ отдаёт положительное количество теплоты.
2) Процесс 2 является изотермическим.
3) В процессе 3 газ совершает работу.
4) В процессе 2 происходит расширение газа при постоянной температуре.
5) В процессе 1 происходит сжатие газа при постоянной температуре.
Работа газа находится как площадь под графиком 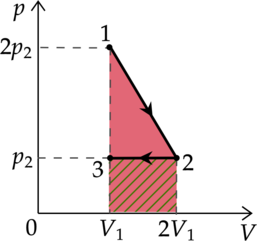
1) Первое начало термодинамики: [Q=Delta U+A] где (Delta U) — изменение внутренней энергии, (A) — работа газа, (Q) — количество теплоты, полученное газом. (Delta U=0), так как температура в процессе 1 не изменяется. При увеличении давления в изотермическом процессе объём уменьшается. (Delta V<0), следоватлеьно, (A<0). Таким образом, (Q<0), то есть газ отдает кол-во теплоты в данном процессе.
Утверждение 1 — (color{green}{smalltext{Верно }})
2) В процессе 2 температура увеличивается.
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) (p=const), следовательно (Vsim T)
Температура уменьшается, то есть объем тоже уменьшается, (Delta V<0), (A<0)
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) В процессе 2 температура увеличивается.
Утверждение 4 — (color{red}{smalltext{Неверно }})
5) Температура в процессе 1 не изменяется. По закону Бойля-Мариотта (p V=const) так как давление увеличивается объём уменьшается.
Утверждение 5 —(color{green}{smalltext{Верно }})
Ответ: 15
На рисунке показан график циклического процесса, проведённого с одноатомным идеальным газом, в координатах (V-T), где (V) — объём газа, (T) — абсолютная температура газа. Количество вещества газа постоянно. 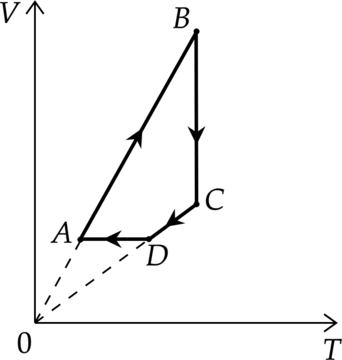
Из приведённого ниже списка выберите два правильных утверждения, характеризующие процессы на графике, и укажите их номера.
1) В состоянии (B) концентрация газа максимальна.
2) В процессе (AB) газ отдаёт некоторое количество теплоты.
3) В процессе (BC) внутренняя энергия газа увеличивается.
4) Давление газа в процессе (CD) постоянно, при этом внешние силы совершают над газом положительную работу.
5) В процессе (DA) давление газа изохорно уменьшается.
1) В точке (B) объем максимален, а концентрация минимальна:
Утверждение 1 —(color{red}{smalltext{Неверно }})
2) Первое начало термодинамики: [Q=Delta U+A] где (Delta U) — изменение внутренней энергии, (A) — работа газа, (Q) — количество теплоты, полученное газом. В процессе (AB) работа равна (0), температура увеличивается, то есть (Delta U>0), значит (Q>0), то есть газ получает тепло
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) Процесс (BC) — изотермический. Внутренняя энергия не меняется.
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) Процесс (СD) — изобарное сжатие. При уменьшении объема внешние силы совершают положительную работу.
Утверждение 4 — (color{green}{smalltext{Верно }})
5) Процесс (DA) — изохорное охлаждение ((psim T)). Следовательно, при уменьшении температуры давление уменьшается.
Утверждение 5 — (color{green}{smalltext{Верно }})
Ответ: 45
Идеальный газ перевели из состояния 1 в состояние 3 так, как показано на графике зависимости давления р газа от объёма V. Количество вещества газа при этом не менялось. 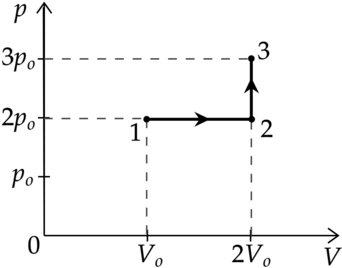
Из приведённого ниже списка выберите два правильных утверждения, характеризующие процессы на графике.
1)Абсолютная температура газа минимальна в состоянии 2.
2)В процессе 1-2 абсолютная температура газа уменьшилась в 2 раза.
3)В процессе 2-3 абсолютная температура газа уменьшилась в 1,5 раза.
4)Плотность газа максимальна в состоянии 1.
5)В ходе процесса 1-2-3 средняя квадратичная скорость теплового движения молекул газа увеличилась в (sqrt{3}) раза.
1) Уравнение состояния газа: [pV=nu RT] где (p) — давление газа, (V) — объем, занимаемый газом, (nu) — количество вещеста, (R) — универасальная газовая постоянная, (T) — температура. Температура максимальна там, где максимально произведение (pV), поэтому из графика видно, что (T_1 – min), (T_3 – max), (T_1<T_2<T_3)
Утверждение 1 — (color{red}{smalltext{Неверно }})
2) Процесс 1-2 — изобарное расширение ((Vsim T)). Объем увеличился в 2 раза, то есть температура тоже увеличилась в 2 раза.
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) Процесс 2-3 — изохорное нагревание. (V=const), следовательно (psim T) Давление увеличивается в 1,5 раза, то есть температура тоже увеличивается в 1,5 раза.
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) В точке 1 — объем минимален, следовательно, плотность там максимальна.
Утверждение 4 — (color{green}{smalltext{Верно }})
5) [E_{k}=dfrac{3}{2}kT] [dfrac{m_0 v^2}{2}=dfrac{3}{2}kT] где (m_0) — масса газа, (v^2) средняя квадратичная скорость [v^2sim T] [vsim sqrt{T}] Температура в процессе 1-2-3 увеличилась в 3 раза, значит средняя квадратичная скорость увеличилась в (sqrt{3}) раз
Утверждение 5 — (color{green}{smalltext{Верно }})
Ответ: 45
Сосуд разделён на две равные по объёму части пористой неподвижной перегородкой. В левой части сосуда содержится 40 г неона, в правой — 2 моль гелия. Перегородка может пропускать молекулы гелия и является непроницаемой для молекул неона. Температура газов одинакова и остаётся постоянной.
Выберите два верных утверждения, описывающих состояние газов после установления равновесия в системе.
1) Внутренняя энергия гелия в сосуде меньше, чем внутренняя энергия неона.
2) Концентрация гелия в левой части сосуда в 2 раза больше концентрации неона.
3) В левой части сосуда общее число молекул газов в 3 раза больше, чем в правой части.
4) Внутренняя энергия гелия в сосуде в конечном состоянии меньше, чем в начальном.
5) В конечном состоянии давление в левой части сосуда в 3 раза больше, чем в правой.
1) Молярная масса неона (M=20) г/моль. Количество неона: [nu=dfrac{m}{M}=dfrac{40text{ г}}{20text{ г/моль}}=2 text{ моль}] Гелий займет все пространство сосуда, значит в левой части будет 3 моля вещества (1 моль гелия и 2 моль неона).
В правой части будет тоже 1 моль гелия.
Внутренняя энергия газа: [U=dfrac{i}{2}nu RT] Газы находятся при одинаковой температуре, количество гелия равно количеству неона. Внутренняя энергия гелия равна внутренней энергии неона
Утверждение 1 — (color{red}{smalltext{Неверно }})
2) В левой части сосуда количество гелия в два раза меньше количества неона. Следовательно, концентрация гелия в два раза меньше концентрации неона.
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) Так как количество вещества в левой части сосуда больше в 3 раза, чем в правой, то и количество молекул также больше в 3 раза.
Утверждение 3 — (color{green}{smalltext{Верно }})
4) Так как температура гелия и общее количество гелия в сосуде не изменилось, то и внутреннняяя энергия не поменялась.
Утверждение 4 — (color{red}{smalltext{Неверно }})
5) Давление газа: [p=nkT] Так как кол-во вещества в левой части сосуда больше в 3 раза, чем в правой, температуры одинаковые, то давление в конечном состоянии больше в левой части в 3 раза, чем в правой.
Утверждение 5 — (color{green}{smalltext{Верно }})
Ответ: 35
Источник
(Все задачи по молекулярно-кинетической теории и ответы к ним находятся в zip-архиве (290 кб), который можно скачать и открыть на своем компьютере. Попробуйте решить задачи самостоятельно и только потом сравнивать свои ответы с нашими. Желаем успехов!)
32.1. Какова внутренняя энергия одноатомного газа, занимающего при температуре T объем V, если концентрация молекул n? [ U = (3/2)nkTV ]
32.2. В цилиндре с площадью основания S = 100 см2 находится газ при температуре t = 27 °С. На высоте h = 30 см от дна цилиндра расположен поршень массой m = 60 кг. Какую работу совершит газ, если его температуру медленно повысить на Δt = 50 °С? Атмосферное давление po = 105 Па. [ A ≅ 79.4 Дж ]
32.3. Газообразный водород массой m = 0,1 кг совершает круговой процесс 1 – 2 – 3 – 1 (рис.). Найдите работу газа на участке 1 – 2, если Т1 = 300 K, a V2 = 3V1. [ A = 2.5×105 Дж ]
32.4. Идеальный газ массой m = 20 г и молярной массой M = 28 г/моль совершает замкнутый процесс (рис.). Температура в точках 1 и 2 равна: T1 = 300 К; Т2 = 496 К. Найти работу газа за цикл. [ A = 1162 Дж ]
32.5. Давление ν молей идеального газа связано с температурой по закону: Т = αp2 (α = const). Найти работу газа при увеличении объема от значения V1 до значения V2. Выделяется или поглощается при этом тепло? [смотрите ответ в общем файле темы]
32.6. В цилиндре под невесомым поршнем находится газ. Поршень связан с дном цилиндра пружиной. Газ расширяется из состояния с параметрами p1, V1 в состояние p2, V2. Определить работу газа. [смотрите ответ в общем файле темы]
32.7. ν молей идеального газа помещены в герметическую упругую оболочку. Упругость оболочки такова, что квадрат объема пропорционален температуре. На сколько изменится энергия оболочки, если газ нагреть от температуры T1 до температуры T2? Какова теплоемкость системы? Теплоемкостью оболочки и внешним давлением пренебречь. [смотрите ответ в общем файле темы]
32.8. При изотермическом процессе газ совершил работу 1000 Дж. На сколько увеличится внутренняя энергия этого газа, если ему сообщить количество теплоты вдвое больше, чем в первом случае, а процесс проводить изохорически? [2000 Дж]
32.9. Найти количество теплоты, сообщенное газу в процессе 1 – 2 (рис.). [ Q = 3pV/4 ]
32.10. Один моль идеального газа совершает процесс 1 – 2 – 3 (рис.). Известны: давление p1, p2 и объем V1, V2. Найти поглощенное газом в этом процессе количество теплоты. [смотрите ответ в общем файле темы]
32.11. Один моль идеального газа нагревают сначала изотермически. При этом он совершает работу 10 Дж. Затем его нагревают изобарически, сообщая ему то же количество теплоты. Какую работу совершает газ во втором случае? [4 Дж]
32.12. Водород массой m = 1 кг при начальной температуре T1 = 300 K охлаждают изохорически так, что его давление падает в η = 3 раза. Затем газ расширяют при постоянном давлении до начальной температуры. Найти произведенную газом работу. [ A = 8.3×105 Дж ]
32.13. Один моль идеального газа переводят из начального состояния 1 в конечное 4 в процессе, представленном на рис. Какое количество теплоты подвели к газу, если ΔT = Т4 − T1 = 100 K? [ Q = 415 Дж ]
32.14. В вертикальном цилиндре под тяжелым поршнем находится газ при температуре T. Масса поршня m, его площадь S, объем газа V. Для повышения температуры газа на ΔT ему сообщили количество теплоты Q. Найдите изменение внутренней энергии газа. Атмосферное давление po, трения нет. [смотрите ответ в общем файле темы]
32.15. Для нагревания некоторого количества газа с молярной массой M = 28 г/моль на ΔT = 14 K при p = const требуется количество теплоты Q = 10 Дж. Чтобы охладить его на ту же ΔT при V = const требуется отнять Q = 8 Дж. Определить массу газа. [ m ≅ 0.48 г ]
32.16. В вертикальном цилиндре на высоте h от дна находится поршень. Под поршнем — идеальный газ. На поршень положили гирю массой m. После установления теплового равновесия с окружающей средой цилиндр теплоизолировали и газ начали нагревать. Какое количество теплоты следует подвести к газу, чтобы поршень вернулся в исходное положение. Трения нет. [ Q = 5mgh/2 ]
32.17. В вертикальном цилиндре под невесомым поршнем находится гелий. Объем гелия Vo, а давление 3po (po – атмосферное давление). Поршень удерживается сверху упорами (рис.). Какое количество теплоты необходимо отнять у гелия чтобы его объем стал Vo/2. Трения нет. [ Q = 17poVo/4 ]
32.18. В цилиндре под поршнем находится ν = 0,5 молей воздуха при температуре T = 300 K. Во сколько раз увеличится объем воздуха при сообщении ему количества теплоты Q = 13,2 кДж? Молярная теплоемкость воздуха при постоянном объеме cV = 21 Дж/(моль • К). [ n = 4 ]
32.19. Теплоизолированный сосуд объемом V = 22,4 л разделен пополам теплопроводящей перегородкой. В первую половину сосуда вводят m1 = 11,2 г азота при температуре t1 = 20 °С, а во вторую – m2 = 16,8 г азота при t2 = 15 °С. Какое давление установится в первой половине после выравнивания температур? Система теплоизолирована. [ p ≅ 86 кПа ]
32.20. Баллон емкостью V1 содержащий ν1 молей газа при температуре T1, соединяют с баллоном емкостью V2, содержащим ν2 молей того же газа при температуре T2. Какие установятся давление и температура. Система теплоизолирована. [смотрите ответ в общем файле темы]
32.21. Над одним молем идеального газа совершается процесс из двух изохор и двух изобар (рис.). Температуры в точках 1 и 3 равны T1 и T3. Определить работу газа за цикл, если точки 2 и 4 лежат на одной изотерме. [смотрите ответ в общем файле темы]
32.22. Моль идеального газа совершает цикл из двух изохор и двух изобар (рис.). Работа газа за цикл A = 200 Дж. Максимальная и минимальная температуры в цикле отличаются на ΔT = 60 К. Отношение давлений на изобарах равно 2. Найти отношение объемов на изохорах. [ ≅ 3 ]
32.23. Внутри цилиндрического сосуда под поршнем массы m находится идеальный газ под давлением p. Площадь поршня S, внешнего давления нет. Вначале поршень удерживается на расстоянии h1 от дна сосуда (рис.). Поршень отпустили. После прекращения колебаний поршень остановился. На каком расстоянии от дна он остановился? Трения нет. Тепловыми потерями и теплоемкостью поршня и цилиндра пренебречь. [смотрите ответ в общем файле темы]
32.24. В гладкой трубке между двумя поршнями массой m находится один моль идеального газа. В начальный момент скорости поршней направлены в одну сторону и равны v и 3v (рис.), а температура газа To. Найти максимальную температуру газа. Внешнего давления и трения нет. [смотрите ответ в общем файле темы]
32.25. В горизонтальном неподвижном цилиндре, закрытом поршнем массы m, находится один моль идеального газа. Газ нагревают. При этом поршень, двигаясь равномерно, приобретает скорость v. Найдите количество теплоты, сообщенное газу. Теплоемкостью сосуда и поршня, а также внешним давлением пренебречь. [ Q = 5mv2/4 ]
32.26. Сосуд, содержащий некоторое количество азота, движется со скоростью v = 100 м/с. На сколько изменится температура азота, если сосуд внезапно остановить? [ ΔT = Mv2/(5R) ]
32.27. В гладкой горизонтальной трубе находятся два поршня массами m и 3m. Между поршнями идеальный газ при давлении po. Объем между поршнями Vo (рис.). Первоначально поршни неподвижны, затем их отпускают. Найти максимальные скорости поршней. Труба длинная, внешнего давления нет. [смотрите ответ в общем файле темы]
32.28. Один моль идеального газа изобарически нагрели на ΔT = 72 K, сообщив ему количество теплоты Q = 1,6 кДж. Найти величину γ = cp/cV. [ γ = 1.6 ]
32.29. Вычислить γ = cp/cV для газовой смеси, состоящей из ν1 = 2 молей кислорода и ν2 = 3 молей углекислого газа. [ γ ≅ 1,6]
32.30. Теплоизолированный небольшой сосуд откачан до глубокого вакуума. Окружающая сосуд атмосфера состоит из идеального одноатомного газа при температуре 300 К. В сосуде открывается небольшое отверстие и он заполняется газом. Какую температуру будет иметь газ в сосуде сразу после заполнения? [500 K]
32.31. Определить скорость истечения гелия из теплоизолированного сосуда в вакуум через малое отверстие. Температура газа в сосуде T = 1000 K, скоростью газа в сосуде пренебречь. [ v ≅ 3.3×103 м/с]
32.32. Горизонтальный цилиндрический сосуд разделен подвижным поршнем. Справа от поршня одноатомный идеальный газ с параметрами: po; Vo; To, слева – вакуум (рис.). Поршень соединен с левым торцом цилиндра пружиной, собственная длина которой равна длине сосуда. Определить теплоемкость системы в этом состоянии. Теплоемкостью поршня и цилиндра пренебречь. Трения нет. [ C = 2poVo/To ]
32.33. Над идеальным двухатомным газом совершают процесс p = αV (α = const). Какова молярная теплоемкость газа в этом процессе? [c = 3R]
32.34. С одним молем идеального одноатомного газа проводят процесс: p = po — αV, где α – известная константа. Определить, при каких значениях объема газ получает тепло, а при каких отдает. Объем в процессе возрастает.
32.35. В процессе расширения азота его объем увеличился на 2 %, а давление уменьшилось на 1 %. Какая часть теплоты, полученной азотом, была превращена в работу? Удельная теплоемкость азота при постоянном объеме cV = 745 Дж/(кг • К). [ ≅ 0.44 ]
32.36. В цилиндрическом горизонтальном сосуде находится гладкий подвижный поршень. Слева и справа от поршня находится по одному молю идеального одноатомного газа. Температура газа в левой части поддерживается постоянной, а газ в правой части нагревается. Найдите теплоемкость газа в правой части в момент, когда поршень делит сосуд пополам. [C = 2R]
32.37. В вертикальном цилиндре под поршнем площадью S и массой m находится 1 моль идеального одноатомного газа. Под поршнем включается нагреватель, мощность которого N. Определите установившуюся скорость движения поршня. Атмосферное давление po, газ теплоизолирован, трения нет. [смотрите ответ в общем файле темы]
32.38. Мыльный пузырь содержит ν молей идеального одноатомного газа. Определить теплоемкость этой системы. Атмосферное давление не учитывать. [ C = 3νR ]
32.39. По трубе, в которой работает электрический нагреватель, пропускают газ (рис.). Определить мощность нагревателя, если разность температур газа на выходе и на входе равна ΔТ = 5 К, а массовый расход газа μ = 720 кг/ч. Молярная теплоемкость газа при постоянном давлении cp = 29,3 Дж/(моль • К), его молярная масса M = 29 г/моль. [ N ≅ 1.01 кВт ]
32.40. Из небольшого отверстия в баллоне с сжатым гелием вытекает струя гелия со скоростью v. Найдите разность температур гелия в баллоне и в струе. Давление в струе считать равным внешнему давлению, скоростью газа в баллоне пренебречь. [ ΔT = Mv2/(5R) ]
32.41. Одинаковые сообщающиеся сосуды закрыты поршнями массой m = 5 кг и M = 10 кг и соединены тонкой трубкой с краном (рис.). Под поршнями идеальный одноатомный одинаковый газ. Сначала кран закрыт, поршень M находится на высоте H = 10 см от дна, а температура одинакова. На какую высоту передвинется поршень m после открытия крана? Система теплоизолирована, атмосферного давления нет. [ 20 см ]
32.42. В горизонтальной открытой трубе сечением S без трения могут двигаться два поршня массами m и M. Начальное расстояние между поршнями l, атмосферное давление po. При закрепленных поршнях воздух между ними откачали, затем поршни отпустили. Какое количество теплоты выделится в результате их абсолютно неупругого столкновения? [ Q = poSl ]
32.43. Один моль идеального газа совершает цикл 1 – 2 – 3 – 1, состоящий из изохоры 1 – 2 и двух процессов, представляемых отрезками прямых в координатах p – V (рис.). Определить работу газа за цикл, если известны: температура T1, Т2 = 4Т1, а также Т2 = Т3. Линия 3 – 1 проходит через начало координат. [ A = 3RT1/2 ]
Источник
