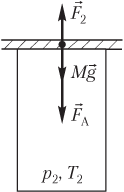В сосуде под поршнем находится масса

5.4. Практическое применение уравнения состояния идеального газа
5.4.3. Уравнение состояния для газа, находящегося в сосуде под поршнем
Для идеального газа, находящегося в сосуде под поршнем, необходимо учитывать следующее:
- масса газа, находящегося в сосуде под поршнем, вследствие изменения термодинамических параметров газа не изменяется:
m = const;
- постоянным остается также количество вещества (газа):
ν = const;
- плотность газа и концентрация его молекул (атомов) изменяются:
ρ ≠ const, n ≠ const.
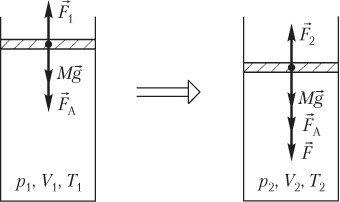
Пусть изменение состояния идеального газа, находящегося в цилиндрическом сосуде под поршнем, вызвано действием на поршень внешней силы F→ (рис. 5.9).
Рис. 5.9
Начальное и конечное состояния газа в сосуде под поршнем описываются следующими уравнениями:
p1V1=νRT1,p2V2=νRT2,}
где p
1, V
1, T
1 — давление, объем и температура газа в начальном состоянии; p
2, V
2, T
2 — давление, объем и температура газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).
Условия равновесия поршня, закрывающего идеальный газ в сосуде (см. рис. 5.9), в начале процесса и в конце процесса выглядят следующим образом:
Mg+FA=F1,Mg+FA+F=F2,}
где M — масса поршня; g — модуль ускорения свободного падения; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление; S — площадь сечения поршня; F
1 — модуль силы давления газа на поршень в начале процесса, F
1 = p
1S; p
1 — давление газа в сосуде в начальном состоянии; F — модуль силы, вызывающей сжатие газа; F
2 — модуль силы давления газа на поршень в конце процесса, F
2 = p
2S; p
2 — давление газа в сосуде в конечном состоянии.
Температура идеального газа, находящегося в сосуде под поршнем, может как изменяться, так и оставаться неизменной:
- если процесс движения поршня происходит достаточно быстро, то температура газа изменяется —
T ≠ const;
- если процесс происходит медленно, то температура газа остается постоянной –
T = const.
Давление идеального газа, находящегося в сосуде под поршнем, также может изменяться или оставаться неизменным:
- если в задаче сказано, что поршень является легкоподвижным, то давление газа под поршнем — неизменно (в том случае, когда из условия задачи не следует обратное) — p = const;
- в остальных случаях давление газа под поршнем изменяется — p ≠ const.
Масса поршня, закрывающего газ в сосуде, либо равна нулю, либо имеет отличное от нуля значение:
- если в задаче сказано, что поршень является легким или невесомым, то масса поршня считается равной нулю —
M = 0;
- в остальных случаях поршень обладает определенной ненулевой массой —
M ≠ const.
Пример 19. В вертикальном цилиндре под легкоподвижным поршнем сечением 250 мм2 и массой 1,80 кг находится 360 см3 газа. Атмосферное давление равно 100 кПа. На поршень поставили гири, и он сжал газ до объема 240 см3. Температура газа при его сжатии не изменяется. Определить массу гирь.
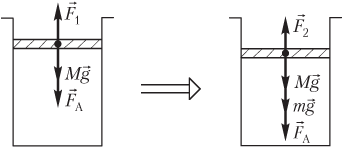
Решение. На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня Mg→;
- сила атмосферного давления F→A;
- сила давления газа F→1, действующая со стороны газа (до его сжатия);
- сила давления газа F→2, действующая со стороны газа (после его сжатия);
- mg→ — вес гирь.
Условие равновесия поршня запишем в следующем виде:
- до сжатия газа —
F
1 = Mg + F
A,
где F
1 — модуль силы давления газа, F
1 = p
1S; p
1 — давление газа до сжатия; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление; g — модуль ускорения свободного падения;
- после сжатия газа —
F
2 = Mg + F
A
+ mg,
где F
2 — модуль силы давления газа, F
2 = p
2S; p
2 — давление газа после сжатия; mg — вес гирь; m — масса гирь.
Считая процесс сжатия газа изотермическим, запишем уравнение Менделеева — Клапейрона для газа под поршнем следующим образом:
- до его сжатия —
p
1V
1 = νRT,
где V
1 — первоначальный объем газа под поршнем; ν — количество газа под поршнем; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа (не изменяется в ходе процесса);
- после его сжатия —
p
2V
2 = νRT,
где V
2 — объем сжатого поршнем газа.
Равенство
p
1V
1 = p
2V
2
и два условия равновесия, записанные в явном виде, образуют полную систему уравнений:
p1S=Mg+pAS,p2S=Mg+pAS+mg,p1V1=p2V2,}
которую требуется решить относительно массы гирь m.
Для этого выразим отношение давлений p
2/p
1 из первой пары уравнений:
p2p1=Mg+pAS+mgMg+pAS
и из третьего уравнения:
p2p1=V1V2,
запишем равенство правых частей полученных отношений:
Mg+pAS+mgMg+pAS=V1V2.
Отсюда следует, что искомая масса определяется формулой
m=(M+pASg)(V1V2−1).
Вычисление дает результат:
m=(1,80+100⋅103⋅250⋅10−610)(360⋅10−6240⋅10−6−1)=2,15 кг.
Указанное сжатие газа вызвано гирями массой 2,15 кг.
Пример 20. Открытый цилиндрический сосуд сечением 10 см2 плотно прикрывают пластиной массой 1,2 кг. Атмосферное давление составляет 100 кПа, а температура окружающего воздуха равна 300 К. На сколько градусов нужно нагреть воздух в сосуде, чтобы он приподнял пластину?
Решение. На рисунке показаны силы, действующие на пластину после нагревания газа:
- сила тяжести пластины Mg→;
- сила атмосферного давления F→A;
- сила давления газа F→2, действующая на пластину со стороны нагретого газа.
Пластина находится в состоянии неустойчивого равновесия; условие равновесия пластины выглядит следующим образом:
F
2 = Mg + F
A,
где F
2 — модуль силы давления нагретого газа, F
2 = p
2S; p
2 — давление нагретого газа; S — площадь сечения сосуда; Mg — модуль силы тяжести пластины; M — масса пластины; g — модуль ускорения свободного падения; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление.
Запишем уравнение Менделеева — Клапейрона следующим образом:
- для газа в сосуде до его нагревания
p
1V = νRT
1,
где p
1 — давление газа в сосуде до нагревания (совпадает с атмосферным давлением), p
1 = p
A; V — объем газа в сосуде; ν — количество вещества (газа) в сосуде; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T
1 — температура газа в сосуде до нагревания (совпадает с температурой окружающей среды);
- для газа в сосуде после его нагревания
p
2V = νRT
2,
где p
2 — давление нагретого газа; T
2 — температура нагретого газа.
Два уравнения состояния газа (до и после нагревания) и условие равновесия пластины, записанные в явном виде, образуют полную систему уравнений:
pAV=νRT1,p2V=νRT2,p2S=Mg+pAS;}
систему необходимо решить относительно температуры T
2, до которой следует нагреть газ.
Для этого делением первой пары уравнений
pAVp2V=νRT1νRT2
получим выражение для давления нагретого газа:
p2=pAT2T1
и подставим его в третье уравнение системы:
pAT2ST1=Mg+pAS.
Преобразуем полученное выражение к виду
T2=T1(Mg+pAS)pAS=T1(MgpAS+1),
а затем найдем разность
ΔT=T2−T1=MgT1pAS.
Произведем вычисление:
ΔT=1,2⋅10⋅300100⋅103⋅10⋅10−4=36 К=36 °С.
Пример 21. В цилиндрическом сосуде поршень массой 75,0 кг и площадью сечения 50,0 см2 начинает двигаться вверх. Давление газа под поршнем постоянно и равно 450 кПа, атмосферное давление составляет 100 кПа. Считая, что поршень движется без трения, определить модуль скорости поршня после прохождения им 3,75 м пути.
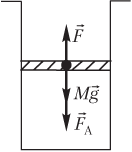
Решение. На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня Mg→;
- сила атмосферного давления F→A;
- сила давления газа F→, действующая на поршень со стороны нагретого газа.
Под действием указанных сил, направленных вверх, поршень движется с ускорением a→:
F→+F→A+Mg→=ma→,
или в проекции на вертикальную ось —
F − F
A − Mg = Ma,
где F — модуль силы давления газа под поршнем, F = pS; p — давление газа; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; g — модуль ускорения свободного падения; a — модуль ускорения поршня.
Преобразуем записанное уравнение, выразив модуль ускорения и выполнив подстановку выражений для модулей сил:
a=F−FA−MgM=(p−pA)SM−g.
Скорость поршня, его ускорение и пройденный путь связаны между собой соотношением
l=v22a,
где l — пройденный путь; v — модуль скорости поршня.
Выразим отсюда модуль скорости поршня:
v=2al
и подставим в записанную формулу выражение для модуля ускорения:
v=2l((p−pA)SM−g).
Выполним расчет:
v=2⋅3,75((450−100)⋅103⋅50⋅10−475,0−10)≈10 м/с.
После прохождения 3,75 м пути поршень приобретет скорость, приблизительно равную 10 м/с.
Источник
8748. Объем сосуда с идеальным газом уменьшили вдвое, выпустив половину газа и поддерживая температуру газа в сосуде постоянной. Как изменятся в результате этого давление газа в сосуде и его внутренняя энергия?
Для каждой величины определите соответствующий характер изменения:
1) не изменится
2) уменьшится
3) увеличится


P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8748.
8780. В цилиндрическом сосуде под поршнем находится газ. Поршень не закреплен и может перемещаться в сосуде без трения (см. рисунок). В сосуд закачивается еще такое же количество газа при неизменной температуре. Как изменится в результате этого давление газа и концентрация его молекул?

Для каждой величины определите соответствующий характер изменения:
1) не изменится
2) уменьшится
3) увеличится


P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8780.
8812. Аргон помещают в открытый сверху сосуд под легкий подвижный поршень и начинают охлаждать, Давление воздуха, окружающего сосуд, равно 105 Па. Начальный объем газа 9 л, начальная температура 450 К. Масса газа в сосуде остается неизменной. Трением между поршнем и стенками сосуда пренебречь.
Установите соответствие между физическими величинами, характеризующими аргон, и формулами, выражающими их зависимость от абсолютной температуры Т газа в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) внутренняя энергия газа ( U(T) )
Б) объем газа ( V(T) )
ФОРМУЛЫ
1) ( dT, d = ) 3 Дж/К
2) ( frac{b}{T}, b = ) 4050 м3 ⋅ K
3) ( at, a = ) 2 ⋅ 10-5 м3/K
4) ( cT, c = ) 20 Дж/К

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8812.
8844. На рисунке показан процесс изменения состояния одного моля одноатомного идеального газа (U – внутренняя энергия газа; p – его давление). Как изменятся в ходе этого процесса объем и теплоемкость газа? Для каждой величины определите соответствующий характер изменения:

1) не изменится
2) уменьшится
3) увеличится


P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8844.
8876. В цилиндре под поршнем находится твердое вещество. Цилиндр поместили в раскаленную печь. На рисунке показан график изменения температуры T вещества по мере поглощения им количества теплоты Q. Какие участки графика соответствуют нагреванию вещества в газообразном состоянии и кипению жидкости?

ТЕПЛОВЫЕ ПРОЦЕССЫ
А) кипение жидкости
Б) нагревание вещества в газообразном состоянии
УЧАСТКИ ГРАФИКА
1) 1
2) 2
3) 3
4) 4

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8876.
8908. При исследовании изопроцессов использовался закрытый сосуд переменного объема, заполненный аргоном и соединенный с манометром. Объем сосуда медленно уменьшают, сохраняя температуру аргона в нем неизменной. Как изменятся при этом внутренняя энергия аргона в сосуде и концентрация его молекул?
Для каждой величины определите соответствующий характер изменения:
1) не изменится
2) уменьшится
3) увеличится


P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8908.
8940. В ходе адиабатного процесса внутренняя энергия 1 моль разреженного гелия увеличивается. Как изменяются при этом температура гелия и его давление?
Для каждой величины определите соответствующий характер изменения:
1) не изменится
2) уменьшится
3) увеличится


P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8940.
8972. Установите соответствие между процессами в идеальном газе и значениями физических величин, характеризующих эти процессы (( Delta U ) – изменение внутренней энергии; ( A ) работа газа, ( nu ) – количество газа).
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
ПРОЦЕССЫ
А) изотермическое сжатие при ( nu = const )
Б) изобарное расширение при ( nu = const )
ЗНАЧЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН
1) ( Delta U > 0,~A = 0 )
2) ( Delta U > 0,~A > 0 )
3) ( Delta U = 0,~A > 0 )
4) ( Delta U = 0,~A

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8972.
9004. Установите соответствие между процессами в идеальном газе и значениями физических величин, характеризующих эти процессы (( Delta U ) – изменение внутренней энергии; ( A ) – работа газа, ( upsilon ) – количество газа).
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
ПРОЦЕССЫ
А) адиабатическое сжатие при ( nu = const )
Б) изохорное нагревание при ( nu = const )
ЗНАЧЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН
1) ( Delta U > 0,~A = 0 )
2) ( Delta U > 0,~A > 0 )
3) ( Delta U = 0,~A > 0 )
4) ( Delta U > 0,~A

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 9004.
9036. Температуру холодильника теплового двигателя, работающего по циклу Карно, увеличили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД теплового двигателя и количество теплоты, отданное газом за цикл холодильнику?
Для каждой величины определите соответствующий характер изменения:
1) не изменилась
2) уменьшилась
3) увеличилась


P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 9036.
Для вас приятно генерировать тесты, создавайте их почаще
Источник
Температуру холодильника тепловой машины Карно понизили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось.
Как изменились при этом КПД тепловой машины и работа газа за цикл?
Для каждой величины определите соответствующий характер её изменения:
- увеличилась
- уменьшилась
- не изменилась
Запишите в поле для ответа последовательность цифр обозначающих изменения, соответствующие физическим величинам “КПД тепловой
машины”,”Работа газа
за цикл”. Цифры в ответе могут повторяться.
Это задание решали 10 тыс. раз. С ним справились 56% пользователей.
В закрытом сосуде с жёсткими стенками находятся в равновесии друг с другом жидкая вода и её пар. Содержимое сосуда немного охлаждают. Как изменятся в результате этого плотность пара в сосуде и масса жидкой воды?
Для каждой величины определите соответствующий характер изменения:
- Плотность пара в сосуде
- Масса жидкой воды
- увеличится
- уменьшится
- не изменится
Запишите в поле для ответа последовательность цифр, соответствующих пунктам АБ. Цифры в ответе могут повторяться.
Показать разбор и ответ
Это задание решали 7 тыс. раз. С ним справились 52% пользователей.
В закрытом сосуде с жёсткими стенками находятся в равновесии друг с другом жидкая вода и её пар. Содержимое сосуда немного подогревают.
Как изменятся в результате этого давление пара в сосуде и масса жидкой воды?
Для каждой величины определите соответствующий характер изменения:
- увеличится
- уменьшится
- не изменится
Запишите в поле для ответа последовательность цифр в порядке, соответствующем величинам: давление пара в сосуде, масса жидкой воды.
Цифры в ответе могут повторяться.
Показать разбор и ответ
Это задание решали 5 тыс. раз. С ним справились 59% пользователей.
В закрытом сосуде с жёсткими стенками находится моля гелия. Из сосуда выпускают половину газа и накачивают в сосуд взамен моля аргона, поддерживая температуру неизменной.
Определите, как в результате этого изменяются следующие физические величины: давление в сосуде, удельная теплоёмкость содержимого сосуда.
Для каждой величины определите соответствующий характер изменения:
- Давление в сосуде
- Удельная теплоёмкость содержимого сосуда
- увеличивается
- уменьшается
- не изменяется
Запишите в поле для ответа последовательность цифр, соответствующих пунктам АБ. Цифры в ответе могут повторяться.
Это задание решали 4 тыс. раз. С ним справились 30% пользователей.
В закрытом сосуде с жёсткими стенками находится моля аргона. Из сосуда выпускают половину газа и накачивают в сосуд взамен моля гелия, поддерживая температуру неизменной.
Определите, как в результате этого изменяются следующие физические величины: концентрация атомов газа в сосуде, удельная теплоёмкость содержимого сосуда.
Для каждой величины определите соответствующий характер изменения:
- Концентрация атомов газа в сосуде
- Удельная теплоёмкость содержимого сосуда
- увеличивается
- уменьшается
- не изменяется
Запишите в поле для ответа последовательность цифр, соответствующих пунктам АБ. Цифры в ответе могут повторяться.
Это задание решали 3 тыс. раз. С ним справились 37% пользователей.
В цилиндрическом сосуде под поршнем находится газ. Поршень не закреплён и может перемещаться в сосуде без трения (см. рисунок). Газ медленно охлаждают. Как изменятся в результате этого давление газа и концентрация его молекул?
Для каждой величины определите соответствующий характер изменения:
- Давление газа
- Концентрация молекул газа
- увеличится
- уменьшится
- не изменится
Запишите в поле для ответа последовательность цифр, соответствующих пунктам АБ. Цифры в ответе могут повторяться.
Это задание решали 7 тыс. раз. С ним справились 30% пользователей.
Коэффициент полезного действия идеальной тепловой машины можно увеличить,
- только уменьшив температуру нагревателя.
- только увеличив температуру холодильника.
- используя в качестве рабочего тела другой газ.
- уменьшив температуру холодильника или увеличив температуру нагревателя.
Это задание решали 11 тыс. раз. С ним справились 59% пользователей.
Источник