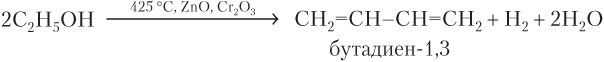В сосуде протекает реакция

Задача 356.
Для реакции Н2(г) + Br2(г) = 2HBr(г) при некоторой температуре К = 1. Определить состав (в процентах по объему) равновесной реакционной смеси, если исходная смесь состояла из 3 молей Н2 и 2 молей Вг2.
Решение:
Уравнение реакции имеет вид:
Н2(г) + Br2(г) = 2HBr(г)
Согласно уравнению реакции из 1 моля Н2 и 1 Br2 образуется 2 моль HBr. Обозначим количество израсходованных исходных веществ через x. Тогда равновесные концентрации реагирующих веществ будут раны:
[Н2] = (3 – х) моль/л, [Br2] = (2 – х) моль/л, [HBr] = (2х) моль/л. Подставив эти значения концентраций в выражение константы равновесия реакции, рассчитаем значение x:

Тогда равновесные концентрации веществ будут равны:
[Н2] = 3 – 0,808 = 2,192 моль/л;
[Br2] = 2 – 0,808 = 1,192 моль/л;
[HBr] = 2 . 0,808 = 1,616 моль/л.
Находим объёмы газов в равновесной системе, учитывая, что 1 моль любого газа при нормальных условиях занимает 22,4л, получим:

Тогда общий объём газовой равновесной системы будет равен 112 л (49,1 + 26,7 + 36,2 = 112).
Теперь определим состав газов (в процентах по объему) равновесной реакционной смеси по формуле:

w% – объёмная доля вещества, выраженная в процентах, V(в-ва) – объём вещества, V(смеси) – общий объём газовой смеси.
Тогда

Ответ: 43,84% Н2; 23,84% Br2; 32,32%HBr.
Задача 357.
Константа равновесия реакции равна единице. Сколько процентов вещества А подвергнется превращению, если смешать З моля вещества А и 5 молей вещества В?
Решение:
Уравнение реакции имеет вид:
А(г) + В(г) = С(г) + D(г)
Согласно уравнению реакции из 1 моля вещества А и 1 моля вещества В образуется по 1 молю веществ С и D. Обозначим равновесные концентрации веществ С и D через x. Тогда равновесные концентрации веществ будут раны: [C] = [D] = моль/л, [A] = (3 – х)моль/л, [B] = (5 – х)моль/л. Подставив эти значения концентраций в выражение кон-станты равновесия реакции, рассчитаем значение x:

Теперь рассчитаем, сколько процентов вещества А подвергнется превращению из пропорции:
3 : 100 = 1,875 : x; x = (1,875 . 100)/3 = 62,5%
Ответ: 62,5%.
Задача 358.
После смешивания газов А и В в системе А(г) + В(г) = С(г) + D(г) устанавливается равновесие при следующих концентрациях: [B] = 0,05 моль/л; [C] = 0,02 моль/л. Константа равновесия реакции равна 4.102. Найти исходные концентрации веществ А и В.
Решение:
Уравнение реакции имеет вид:
А(г) + В(г) = С(г) + D(г) .
Согласно уравнению реакции из 1 моля вещества А и 1 моля вещества В образуется по 1 молю веществ С и D.
Поскольку по условию задачи в каждом литре системы образовалось 0,02 моля вещества С, то такое же количество образовалось вещества D, было израсходовано по 0,02 моля веществ А и В.
Сначала найдём концентрацию вещества А из выражения для константы равновесия реакции:

Отсюда рассчитаем искомые исходные концентрации веществ А и В:
[A]0 = 0,2 + 0,02 = 0,22 моль/л;
[B]0 = 0,05 + 0.02 = 0,07 моль/л.
Ответ: [A]0 = 0,22 моль/л; [B]0 = 0,07 моль/л.
Задача 359.
Найти константу равновесия реакции N2O4 ⇔ 2NO2, если начальная концентрация N2O4 составляла 0,08 моль/л, а к моменту наступления равновесия диссоциировало 50% N2O4.
Решение:
Уравнение реакции имеет вид: N2O4 ⇔ 2NO2. Из уравнения реакции следует, что из 1 моля N2O4 образуется 2 моля NO2. Поскольку по условию задачи 50% N2O4 диссоциировало, то количество N2O4, продиссоциировавшегося составляет 0,04 моль/л (0,08 . 0,5 = 0,04).
Тогда равновесные концентрации участвующих веществ будут равны:
[N2O4]0 = 0,08 – 0,04 = 0,04 моль/л;
[NO2]0 = 0,04 .2 = 0,08 моль/л
Выражение для константы равновесия для данной реакции будет иметь вид:

Подставляя в это выражение данные из задачи, получим:

Ответ: 0,16
Задача 360.
В замкнутом сосуде протекает реакция АВ(г) ⇔ А(г) + В(г) Константа равновесия реакции равна 0,04, а равновесная концентрация вещества В составляет 0,02 моль/л. Найти начальную концентрацию вещества АВ. Сколько процентов вещества АВ разложилось?
Решение:
Уравнение реакции имеет вид: АВ(г) ⇔ А(г) + В(г). Из уравнения реакции следует, что из 1 моля вещества АВ образуется 1 моль вещества А и 1 моль вещества В. Поскольку по условию задачи в каждом литре системы образовалось 0,02 моля вещества В, то столько же образовалось и вещества А, при этом было израсходовано 0,02 моля вещества АВ.
Константа равновесия данной реакции выражается уравнением

Подставляя в это выражение данные задачи, рассчитаем равновесную концентрацию вещества АВ:

Таким образом, искомая исходная концентрация вещества АВ будет равна:
[AB]0 = 0,02 + 0,01 = 0,03 моль/л
Сколько процентов вещества АВ разложилось находим из пропорции:
0,03 : 100 = 0,02 : х = (0,02 . 100)/0,03 = 66,7%
Ответ: [AB]0 = 0,03 моль/л; 66,67%.
Источник
9. Скорость химической реакции. Химическое равновесие
9.1. Скорость химической реакции: общие положения
Быстроту протекания химической реакции характеризует скорость.
Скорость гомогенной реакции
v — это изменение химического количества вещества в единицу времени и в единице объема:
v = ±∆n/(V∆t), (9.1)
где Δn — изменение химического количества исходного вещества или продукта реакции; V — объем реакционной системы; Δt — промежуток времени, за которое произошло данное изменение химического количества.
В выражении (9.1) знак минус используется, если скорость реакции рассчитывают по данным для исходных веществ: в этом случае (рис. 9.1) значение Δn < 0, так как n(t
2) < n(t
1), а скорость реакции может быть величиной только положительной. Если скорость определяют по данным для продуктов реакции, то n(t
2) > n(t
1), поэтому Δn > 0, что соответствует знаку плюс в выражении (9.1).
Рис. 9.1. Характер изменения со временем химического количества n или молярной концентрации c для исходных веществ (а) и продуктов реакции (б)
При неизменном объеме отношение Δn/V равно изменению молярной концентрации Δc, поэтому можно сказать, что скорость гомогенной реакции — это изменение молярной концентрации исходного вещества или продукта реакции за единицу времени:
v = ±∆c/∆t. (9.2)
Очевидно, что выражения (9.1) и (9.2) позволяют рассчитывать не мгновенную скорость реакции (т.е. скорость в данный момент времени), а среднюю скорость за промежуток времени Δt. Отметим также, что при разных значениях стехиометрических коэффициентов для различных исходных веществ или продуктов можно получить разные значения скорости. Например, для реакции, протекающей по уравнению
А + 2В = 3С,
скорость, рассчитанная по изменению концентрации вещества С, в 3 раза больше скорости, найденной по веществу А, и в 1,5 раза — по веществу В. Другими словами, отношение скоростей пропорционально отношению стехиометрических коэффициентов, что и неудивительно, так как коэффициенты показывают мольные отношения веществ, участвующих в химической реакции.
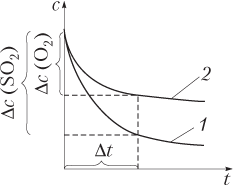
В качестве примера на рис. 9.2 показано изменение со временем концентраций оксида серы(IV) и кислорода для реакции
2SO2 + O2 = 2SO3.
Рис. 9.2. Характер изменения молярной концентрации с в реакции 2SO2 + O2 = 2SO3:
1 — для SO2; 2 — для O2
Из рисунка видно, что за один и тот же промежуток времени Δt изменение концентрации SO2 существеннее, чем O2, поэтому скорость реакции, рассчитанная по данным для оксида серы(IV), будет больше. Чтобы получить одинаковое значение скорости, изменение концентрации делят на стехиометрические коэффициенты. В данном случае
v=–Δc(SO2)2⋅Δt=–Δc(O2)Δt=Δc(SO3)2⋅Δt.
Пример 9.1.
В замкнутом сосуде протекает реакция, описываемая уравнением
А(г) + В(г) = АВ(г).
Скорость реакции равна 0,05 моль/(дм3 ⋅ с), начальная концентрация вещества В составляет 1,5 моль/дм3. Рассчитайте время (с), через которое концентрация вещества В станет равной 1,0 моль/дм3.
Решение. Из формулы (9.2) следует, что
t=Δcv или t=1,5−1,00,10=5 (с).
Ответ: 5 с.
Пример 9.2.
В замкнутом сосуде объемом 2,5 дм3 со скоростью 0,05 моль/(дм3 ⋅ с) протекает гомогенная реакция А + В = АВ.
Найдите массу образовавшегося через 40 с вещества АВ, если его молярная масса равна 64 г/моль.
Решение. Из формулы (9.1) следует:
Δn = vVΔt = 0,05 ⋅ 2,5 ⋅ 40 = 5 (моль),
m(AB) = Δn(AB) ⋅ M(AB) = 5 ⋅ 64 = 320 (г).
Ответ: 320 г.
Гетерогенные реакции протекают на границе раздела фаз: тв–тв, тв–ж, ж–г, тв–г, поэтому под скоростью гетерогенной реакции понимается изменение химического количества реагента или продукта в единицу времени на единице площади межфазной поверхности S
м.п:
v=±ΔnΔt⋅Sм.п.
Например, в случае реакции CaO (тв) + CO2 (г) = CaCO3 (тв) S
м.п — это площадь поверхностного слоя оксида кальция.
Как правило, со временем скорость химической реакции уменьшается, так как при этом реагирующие вещества расходуются и их концентрация уменьшается.
На скорость химической реакции также влияют:
1) природа реагирующих веществ: например, магний реагирует с водой медленно, а литий — быстро. Решающее значение имеет прочность связи в молекулах реагирующих веществ: медленно протекают реакции с участием азота, ибо прочность связи в молекуле N2 очень большая;
2) концентрация реагирующих веществ: чем больше концентрация, тем чаще частицы сталкиваются между собой, тем выше скорость реакции.
Скорость одностадийной (т.е. протекающей в одну стадию при непосредственном столкновении указанных в уравнении реакции частиц) гомогенной реакции
аА + bВ → продукты
пропорциональна произведению молярных концентраций реагирующих веществ, возведенных в степень, равную соответствующему стехиометрическому коэффициенту
v = kc
a
(A)c
b
(B),
где k — константа скорости реакции, равная скорости при c
a
(A) · c
b
(B) = 1;
3) давление: для реакций, протекающих с участием газов, скорость реакции возрастает с увеличением давления (при этом пропорционально возрастает концентрация) и падает, если давление уменьшается (пропорционально уменьшается концентрация);
4) площадь соприкосновения реагирующих веществ (в случае гетерогенных реакций): чем больше площадь соприкосновения реагирующих веществ, тем выше скорость реакции (например, железные опилки быстрее растворяются в соляной кислоте, чем такой же по массе железный гвоздь). Отметим, что скорость гетерогенных реакций не зависит от содержания твердого вещества, а зависит только от концентрации веществ в жидком или газообразном состоянии;
5) воздействие различных видов излучения (ультрафиолетовый свет, γ-лучи), которое приводит к образованию в системе чрезвычайно реакционных способных частиц, содержащих неспаренные электроны. Такие частицы называются свободными радикалами, например
Cl2 →hv 2Cl• (быстро и при комнатной температуре протекает реакция между содержащими неспаренные электроны молекулами NO и O2);
6) температура: экспериментально установлено, что при повышении температуры на каждые 10 °С скорость реакций (не всех и только при небольшом интервале ΔТ) возрастает в 2–4 раза (правило Вант-Гоффа). Число, показывающее, во сколько раз увеличивается скорость реакции при повышении температуры на 10 °С, называется температурным коэффициентом реакции (γ). Математически зависимость скорости реакции от температуры задается уравнением
v(T2)=v(T1)γ(T2−T1)/10.
С ростом температуры возрастает скорость как экзотермических, так и эндотермических реакций
7) катализаторы — вещества, ускоряющие (положительный катализ) или замедляющие (отрицательный катализ) химическую реакцию за счет того, что направляют ее по другому пути, но сами в результате остающиеся без химических изменений. Различают гомогенный и гетерогенный катализ: в первом случае катализатор и реагенты находятся в одной фазе (C2H5OH →H2SO4 C2H4 + H2O), а во втором — в разных
(4NH3 + 5O2 →Pt 4NO + 6H2O);
8) природа растворителя: в случае реакций, протекающих в растворах: ионные реакции быстрее протекают в более полярных растворителях и растворителях с большим значением диэлектрической проницаемости, поскольку эти факторы способствуют диссоциации электролитов;
9) перемешивание: скорость гетерогенных (но не гомогенных) реакций возрастает при перемешивании, так как это способствует более эффективному отводу продуктов реакции от границы раздела фаз.
Возрастание скорости реакции с ростом температуры обусловлено увеличением числа активных молекул. Дело в том, что далеко не всякое столкновение молекул сопровождается образованием продукта (если бы это было так, то все реакции в газовой фазе или растворах протекали бы мгновенно). Результативным будет столкновение не всех, а только тех молекул, которые в момент столкновения обладают повышенной энергией. Такие молекулы называются активными. Можно сказать, что активными называют молекулы, энергия которых достаточна для того, чтобы столкновение между ними привело к образованию продукта (в реальной химической системе таких молекул сравнительно мало).
Разность между запасом энергии активных молекул и средней энергией молекул в системе реагирующих веществ называется энергией активации. Таким образом, энергия активации — это энергия, которую нужно сообщить реагирующим частицам для того, чтобы они стали активными и их столкновение привело к химической реакции.
Активная молекула по сравнению с обычной может обладать повышенной кинетической энергией, повышенной энергией электронного состояния и др.
Энергию активации можно рассматривать как некий энергетический барьер, препятствующий протеканию реакции. Понятно, что чем больше величина этого барьера, т.е. выше энергия активации, тем меньше скорость химической реакции и наоборот. В обратимых процессах для эндотермических реакций Е
а всегда больше, чем для экзотермических, поэтому скорость эндотермических реакций сильнее зависит от температуры. Энергию активации можно сравнить с высотой планки для прыгунов в высоту: меньше высота планки — больше прыгунов преодолевают высоту (скорость реакции больше); при повышении высоты планки число спортсменов, преодолевающих высоту, уменьшается (уменьшается скорость реакции).
Практически с нулевой энергией активации протекают реакции между свободными радикалами или ионами в водном растворе. На энергетических схемах реакции (рис. 9.3) энергию активации Е
а показывают с помощью колоколообразной кривой, высота которой равна Е
а реакции.
На этих кривых показан тепловой эффект химической реакции Q:
Q = E(реагентов) − E(продуктов).
В данном случае Q > 0.
Рис. 9.3. Энергетическая схема экзотермической реакции
Ускоряющее действие катализатора обусловлено тем, что он снижает энергию активации реакции, направляя ее (реакцию) по другому пути. Отметим, что на тепловой эффект реакции катализатор не влияет. В качестве катализаторов наиболее часто используются некоторые простые вещества (Pt, Pd, Ni, Fe), некоторые оксиды (MnO2, V2O5, Cr2O3, Al2O3, CuO), а также смеси указанных веществ. Катализаторы, ускоряющие химические реакции в организмах человека и животных, называются ферментами.
Сущность действия катализатора (при гомогенном катализе) можно показать уравнениями реакций:
А2 + Кат = 2 А ⋅ Кат (быстро) — стадия 1;
2А ⋅ Кат + В2 = 2АВ + Кат (быстро) — стадия 2,
и заключается она в том, что катализатор с большой скоростью образует некоторое промежуточное соединение с одним из реагирующих веществ, которое затем также быстро взаимодействует со вторым исходным веществом с образованием продукта реакции. Катализатор в конце процесса выделяется в химически неизменном виде.
Температурная зависимость скорости реакции
Зависимость скорости реакции от температуры обусловлена зависимостью от температуры константы скорости. Характер этой зависимости для v и k совершенно одинаковый был установлен в конце XIX в. голландским химиком Я. Вант-Гоффом.
Математическое выражение правила Вант-Гоффа:
k(T2)k(T1)=v(T2)v(T1)=γ(T2−T1)/10,
где v(T
1), v(T
2), k(T
1), k(T
2) — скорости и константы скорости соответственно при начальной T
1 и конечной T
2 температуре, выраженной в градусах Кельвина.
Коэффициент γ называют температурным коэффициентом реакции. Он показывает, во сколько раз возрастает скорость реакции при повышении температуры на 10 °C:
γ=k(T+10)k(T)=v(T+10)v(T)=2÷4.
Чем выше скорость реакции, тем меньше время t ее протекания, т.е. значения v и t связаны обратно пропорциональной зависимостью:
v2v1=t1t2.
Правило Вант-Гоффа имеет довольно ограниченное применение. Более точное соотношение между константой скорости и температурой установил в 1889 г. шведский химик С. Аррениус:
k=A⋅e−Eα/RT,
где А — постоянный множитель, не зависящий от температуры и концентрации; e — основание натурального логарифма, e = 2,718; E
α — энергия активации реакции (величина положительная, выражается в килоджоулях на моль); R — универсальная газовая постоянная, R = 8,31 Дж/(моль · К).
В выражении константы скорости показатель степени e−Ea/RT отрицательный, поэтому:
- с повышением температуры константа скорости и скорость реакции возрастают;
- чем больше энергия активации, тем сильнее константа скорости и скорость реакции зависят от температуры.
Сомножитель e−Ea/RT пропорционален доле сталкивающихся молекул, способных к химическому превращению, т.е. доле активных молекул. Доля активных молекул сильно зависит от энергии активации и температуры: чем больше энергия активации, тем меньше в системе активных молекул, тем ниже скорость реакции. При обычных условиях реакции с Е
а
> 120 кДж/моль практически не протекают; очень велика скорость реакций с Е
а
< 40 кДж/моль.
Доля активных молекул от их общего числа для большинства реакций при обычных условиях мала. Так, даже для очень быстрой реакции водорода с атомами хлора, требующей малой энергиии активации (Е
а
= = 23 кДж/моль), доля активных молекул при 20 °С (293 К) составляет 2,72−23 000/(8,31 · 293) ≈ 10−4, т.е. только одна из 10 тысяч молекул активная и имеет достаточную энергию для химического превращения.
С повышением температуры доля активных молекул быстро растет, так как температура в уравнении Аррениуса входит в показатель степени. Например, для реакции, протекающей с Е
а
= 200 кДж/моль, повышение температуры с 298 К до 398 К, т.е. на 100 °К увеличивает долю активных молекул в 109 раз.
Как уже отмечалось, энергию активации Е
а можно представить как своего рода энергетический барьер на пути протекания реакции. Природа этого энергетического барьера двоякая. Во-первых, для реакции необходимо столкновение реагирующих частиц, чему препятствует отталкивание их электронных оболочек. Этот фактор, очевидно, практически не имеет значения для реакций между противоположно заряженными частицами, поэтому реакции в растворах электролитов имеют малую энергию активации и протекают очень быстро. Во-вторых, происходящая в результате реакции перестройка химических связей и перераспределение электронов (т.е. образование переходного состояния) тоже связаны с затратами энергии.
Энергия активации всегда положительная. На схемах наличие энергетического барьера в виде энергии активации изображают колоколообразной кривой, высота которой пропорциональна энергии активации (рис. 9.4). Напомним, что тепловой эффект химической реакции Q равен разности энергий исходных веществ и продуктов. Для прямого процесса
Q = Е(А + В) − Е(АВ),
для обратного
Q = Е(АВ) − Е(А + В).
Рис. 9.4. Энергетические схемы обратимой реакции А + В ⇄ АВ в случае экзотермического (а) и эндотермического (б) прямых процессов
На рис. 9.4 вершина кривой соответствует переходному состоянию (активированному комплексу), которое существует очень короткое время (~ 10−10 с) и распадается с образованием продуктов реакции. Переходное состояние можно представить как комплекс с очень непрочными связями А⋅⋅⋅В.
Из рис. 9.4 следует:
- энергия активации равна разности энергий переходного состояния и исходных веществ (или продуктов);
- энергия активации обратной и прямой реакций отличается на величину теплового эффекта;
- тепловые эффекты прямой и обратной реакций равны по абсолютной величине, но противоположны по знаку;
- в обратимом процессе энергия активации эндотермической реакции всегда больше энергии активации экзотермической реакции на величину теплового эффекта.
Неравенство значений Е
а для экзо- и эндотермических реакций приводит к тому, что влияние температуры на скорость этих реакций также не одинаковое и сильнее выражено для эндотермического процесса (Е
а
больше). Иными словами, при повышении температуры скорость эндотермической реакции возрастает в большее число раз, чем экзотермической, а при понижении температуры скорость уменьшается также в большее число раз. Такое различие приводит к температурному смещению равновесия в обратимых реакциях в направлении, определяемом принципом Ле Шателье.
Роль катализатора заключается в том, что он уменьшает энергию активации реакции, направляя ее по другому пути за счет образования активированного комплекса с одним из реагентов.
Катализатор может снизить Е
а
реакции на несколько десятков килоджоуль на моль, а скорость реакции при этом возрастает в сотни тысяч раз. В обратимых процессах катализатор снижает энергию активации как прямой, так и обратной реакции, и в одинаковое число раз (в одинаковой степени), поэтому катализатор не смещает химическое равновесие, не увеличивает выход продукта, а только ускоряет момент наступления равновесия.
При гомогенном катализе схему процесса в присутствии катализатора К (рис. 9.5) можно представить так (с катализатором взаимодействует вещество А):
- А + К → А⋅⋅⋅К (активированный комплекс) → АК, энергия активации E
a1; - АК + В → АК⋅⋅⋅В (активированный комплекс) → АВ + К, энергия активации E
a2.
Каждый из этих процессов имеет меньшую энергию активации, чем процесс без участия катализатора.
На рис. 9.5 ∆E
a показывает величину, на которую уменьшается энергия активации реакции в присутствии катализатора.
Рис. 9.5. Энергетическая схема хода реакции А + В → АВ:
1 — без катализатора; 2 — в присутствии катализатора
В случае гетерогенного катализа (рис. 9.6) катализатор и реагент находятся в разных агрегатных состояниях и между их фазами имеется граница раздела, например, поверхность твердого катализатора. Именно на ней и осуществляется катализ. При этом молекулы одного из реагентов, например A2, адсорбируются на поверхности катализатора К, в результате чего химические связи в этих молекулах ослабляются и они переходят в активное состояние (A2*). Быстро реагируя с молекулами другого реагента B2, они образуют на поверхности катализатора активные молекулы продукта реакции AB*. Они отрываются от поверхности катализатора, превращаясь в молекулы продукта реакции AB. При этом, как и в случае гомогенного катализа, энергия активации реакции уменьшается, что ведет к увеличению ее скорости.
Рис. 9.6. Схема гетерогенного катализа реакции A2 + B2 = 2AB
Отметим, что для одной и той же реакции изменение природы катализатора может существенно повлиять на природу продуктов реакции, например:
Источник