В сосуде разделенном на равные части неподвижной непроницаемой

Число молекул, относительные скорости которых заключены в данном интервале (распределение Максвелла)

(II.10)

Относительная скорость молекул

(II.11)

Формула изменения концентрации молекул с высотой

(II.12)

Барометрическая формула

(II.13)

где и – давление, и – концентрация газа на высоте и ;

– молярная масса газа; – ускорение свободного падения.

Средняя квадратичная скорость молекул

.(II.14)

Средняя арифметическая скорость молекул

.(II.15)

Наиболее вероятная скорость

,(II.16)

где – масса одной молекулы.

ЗАДАЧА № II.33В законе распределения Максвелла для газовых молекул по скоростям кривая распределения асимптотически приближается к оси скоростей. Означает ли это, что молекулы газа, пусть с малой вероятностью, но могут иметь сколь угодно большие скорости?

Ответ: Скорость молекул ограничена определенным значением энергии теплового движения газа при данной температуре.

ЗАДАЧА № II.34 Возможны ли в газе с температурой К неподвижные молекулы?

Ответ: Их вероятность исчезающее мала, т.к. кривая распределения Максвелла проходит через начало координат.

ЗАДАЧА № II. 35Какой вид приобретет барометрическая формула на большой высоте?

Ответ:С высотой ускорение свободного падения уменьшается, поэтому необходимо использовать потенциальную энергию гравитационного поля

, и барометрическая формула примет вид , где – масса Земли, – масса молекулы газа.

ЗАДАЧА № II.36Как можно трактовать нормировку функции распределения Максвелла, а именно

Ответ:Как достоверное событие, имеющее вероятность равную единице.

ЗАДАЧА №II.37Почему отличаются по своему значению средняя квадратичная, средняя арифметическая и наиболее вероятная скорости газовых молекул?

Ответ:Это вызвано асимметричностью кривой распределения Максвелла.

ЗАДАЧА№ II.38Почему с повышением температуры газа вместе с расширением кривой распределения понижается ее максимум?

Ответ: Это следует из условия нормировки, а следовательно из постоянства площади под кривой.

ЗАДАЧА № II.39Влияют ли на максвелловское распределение молекул по скоростям параметры состояния газа?

Ответ:Влияет только температура.

ЗАДАЧА № II.40Если число молекул в сосуде увеличили, не изменив температуры, то как изменится число молекул, обладающих наиболее вероятной скоростью в максвелловском распределении молекул по скоростям?

Ответ: Число молекул, обладающих наиболее вероятными скоростями, увеличится.

ЗАДАЧА № II.41 В трех одинаковых сосудах при равных условиях находится одинаковое количество азота (N2), гелия (He), и водорода (H2). На рис. 27 дано распределение скоростей этих молекул. Каким кривым распределения соответствуют молекулы водорода и азота?

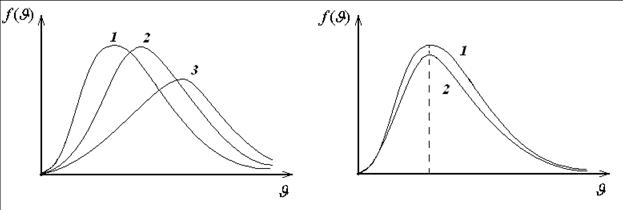
Рисунок 27- Распределение скоростей Рисунок 28- Кривые 1 и 2

молекул

Ответ: Водороду – 3, азоту – 1. Наиболее вероятная скорость , она зависит от молярной массы газа и будет наименьшей для азота, ( г/моль) и наибольшей у водорода ( г/моль).

ЗАДАЧА № II.42 В сосуде, разделенном на равные части неподвижной непроницаемой перегородкой, находится газ. Температуры газа в каждой части сосуда равны, масса газа в левой части больше, чем в правой . Какими кривыми (рис.28) будут описываться функции распределения молекул по скоростям для молекул газа в правой и левой частях сосуда?

Ответ: Газ в обеих частях сосуда одинаковый, температуры равны, следовательно наиболее вероятные скорости молекул тоже равны . Массы разные . В большей массе будет большее число молекул, следовательно, будет больше площадь под кривой функции распределения

. Кривая 1 – для левой части, кривая 2 – для правой части.

ЗАДАЧА № II.43 Определить долю молекул водорода, модули скоростей которых при температуре 27° С лежат в интервале от 1898 м/с до 1902 м/с.

Дано: кг/моль;

К;

м/с;

м/с.

Найти:

Решение

В данной задаче удобнее воспользоваться распределением молекул по относительным скоростям. Доля молекул , относительные скорости которых заключены в интервале от до , определяется формулой

, (1)

где – наиболее вероятная скорость; .

С учетом этих выражений формула (1) примет вид

.

Для удобства сначала вычислим

(м/с),

и отношение скоростей .

Подставим численные значения в (1) и найдем долю молекул водорода, модули скоростей которых лежат в интервале от до

.

ЗАДАЧА № II.44Броуновские частицы с массой 4 фгведут себя в тепловом движении подобно гигантским молекулам, и к ним можно применить закономерности молекулярно-кинетической теории. Исходя из этого, определить, во сколько раз уменьшится концентрация броуновских частиц при увеличении высоты на 1 мм. Температуру принять равной 300 К.

Дано: фг г кг;

мм м;

К.

Найти:

Решение

Для броуновских частиц воспользуемся распределением молекул по

высоте (распределение Больцмана)

,

где и – концентрация молекул на высоте и на высоте , соответственно. Выразим

Прологарифмируем и подставим численные значения,

.

Итак, то есть концентрация частиц уменьшится в раз.

ЗАДАЧА № II.45 На какой высоте над уровнем моря атмосферное давление составляет 78 кПа, если температура воздуха 170С и не меняется с высотой, а давление на уровне моря нормальное? Найти число частиц в единице объема на этой высоте.

Дано: C К;

Па;

Па;

кг/моль.

Найти:

Решение

Если температура не меняется с высотой, то для нахождения давления можно воспользоваться барометрической формулой (II.13)

логарифмируя эту формулу, получаем

Отсюда находим

м; м-3.

ЗАДАЧА № II.46Найти число молекул водорода, заключенных в 1см3 при нормальных условиях, а также число молекул значения скоростей которых лежат в интервале между 399 и 401 м/с.

Дано: см3 м3;

Па;

К;

м/с;

м/с;

кг/моль;

Найти:

Решение

Число молекул можно найти из распределения Максвелла, заданного в виде уравнения (II.10)

Для всех газов при нормальных условиях число молекул в 1 см3 одно и то же и равно см-3 (число Лошмидта).

Вычислим значения величин, входящих в распределение Максвелла

, м/с;

м/с; м/с;

ЗАДАЧА № II.47Температура окиси азота (NO) 300 К. Определить долю молекул, скорость которых лежит в интервале от 820 м/с до 830 м/с.

Дано: К;

м/с;

м/с;

кг/моль.

Найти:

Решение

Рассматриваемый газ находится в равновесном состоянии. Согласно распределению Максвелла, относительное число молекул, скорость которых заключена в интервале от до , ,

где – функция распределения Максвелла, которую можно представить в виде: где м/с.

Тогда

с/м.

Аналогично подсчитаем с/м.

В условии задачи требуется определить долю молекул, скорости которых лежат в диапазоне м/с.

Если в этом пределе функцию Максвелла можно с достаточной степенью точности считать постоянной, то искомая величина может быть рассчитана по приближённой формуле

т.е. Это значит, что при использовании этой формулы допускается ошибка, относительная величина которой

.

Следовательно, с указанной степенью точности можно использовать равенство , или .

Источник

Источник

Молекулярная физика

В трех одинаковых сосудах при равных условиях находится одинаковое количество водорода, гелия и азота A) Распределение скоростей молекул водорода будет описывать кривая B) Распределение скоростей молекул гелия будет описывать кривая C) Распределение скоростей молекул азота будет описывать кривая	A)   B)   C)
В трех одинаковых сосудах находится одинаковое количество газа, причем T1 >T2>T3 A) Распределение скоростей молекул в сосуде с температурой T1описывает кривая B) Распределение скоростей молекул в сосуде с температурой T2описывает кривая C) Распределение скоростей молекул в сосуде с температурой T3описывает кривая	A)   B)   C)
В сосуде, разделенном на равные части неподвижной непроницаемой перегородкой, находится газ. Температуры газа в каждой части сосуда равны, по массе газа в левой части больше, чем в правой M1 > M2. Функция распределения скоростей молекул газа в сосуде будет описываться кривыми
На рисунке представлен график функции (распределения Максвелла), где f (υ) = dN/(Ndυ) – доля молекул, скорости которых заключены в интервале скоростей от υ до υ+dυ в расчете на единицу этого интервала. Для этой функции верным утверждением является…	1. С ростом температуры площадь под кривой растет. 2. С ростом температуры максимум кривой смещается вправо. 3. С ростом температуры величина максимума растет.   A) при понижении температуры величина максимума уменьшается B) положение максимума кривой зависит как от температуры, так и от природы газа C) при понижении температуры площадь под кривой уменьшается
На рисунке представлен график функции (распределения Максвелла). Используя максвелловскую функцию распределения молекул по скоростям, можно:	1. Доказать, что молекулы движутся с определенной скоростью u. 2. Сделать вывод о направлении скорости u. 3. Рассчитать вероятность того, что скорость молекул находится в интервале от u до u+du 4. Рассчитать вероятность того, что скорость молекул равна u. 5. Доказать, что скорости молекул отличны друг от друга, но постоянны.
На рисунке представлен график функции (распределения Максвелла), где f (υ) = dN/(Ndυ) – доля молекул, скорости которых заключены в интервале скоростей от υ до υ+dυ в расчете на единицу этого интервала. Если, не меняя температуры взять другой газ с меньшей молярной массой и таким же числом молекул, то…	A) максимум кривой сместится вправо в сторону больших скоростей B) площадь под кривой уменьшится C) величина максимума увеличится
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где – доля молекул, скорости которых заключены в интервале скоростей от до в расчете на единицу этого интервала. Для этой функции верными являются утверждения, что …	с увеличением температуры максимум кривой смещается вправо при изменении температуры площадь под кривой не изменяется с увеличением температуры величина максимума функции увеличивается при изменении температуры положение максимума не изменяется
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где – доля молекул, скорости которых заключены в интервале скоростей от до в расчете на единицу этого интервала. Для этой функции неверными являются утверждения, что …	при понижении температуры величина максимума функции уменьшается при понижении температуры площадь под кривой уменьшается с ростом температуры наиболее вероятная скорость молекул увеличивается положение максимума кривой зависит не только от температуры, но и от природы газа
На рисунке представлены графики зависимости концентрации молекул идеального газа от высоты над уровнем моря для двух разных температур – (распределение Больцмана). Для графиков этих функций верными являются утверждения, что …
Зависимости давления идеального газа во внешнем однородном поле силы тяжести от высоты для двух разных температур представлены на рисунке. Для графиков этих функций неверными являются утверждения, что …
На рисунке представлены графики функции распределения молекул идеального газа по скоростям (распределение Максвелла), где – доля молекул, скорости которых заключены в интервале скоростей от до в расчете на единицу этого интервала. Для этих функций верными являются утверждения, что …	распределение 1 соответствует газу, имеющему наибольшую массу молекул распределение 3 соответствует газу, имеющему наибольшую температуру распределение 1 соответствует газу, имеющему наименьшую массу молекул распределение 3 соответствует газу, имеющему наименьшую температуру

Средняя энергия молекул

Средняя кинетическая энергия молекул газа при температуре Т зависит от их структуры, что связано с возможностью различных видов движения атомов в молекуле. A) Средняя кинетическая энергия молекул гелия (Не) равна… B) При условии, что имеют место только поступательное и вращательное движение, средняя энергия молекул азота (N2) равна …	1/2kT 3/2kT 5/2kT 6/2kT 7/2kT
Средняя кинетическая энергия молекулы идеального газа при температуре Т равна ε = i/2kТ. Здесь i=nn+nвр+2nk, где nn,nвр и 2nk – степени свободы поступательного, вращательного и колебательного движений молекулы. A) При условии, что имеет место только поступательное и вращательное движение, для молекулярного водорода средняя кинетическая энергия молекул равна… B) При условии, что имеют место только поступательное и вращательное движение, для водяного пара (Н2О) число i равно … C) При условии, что имеют место только поступательное и вращательное движение, для водорода (Н2) число i равно … D) При условии, что имеют место только поступательное и вращательное движение, средняя энергия молекул азота (N2) равна …	A) 1/2kT 3/2kT 5/2kT 6/2kT B) C) D) 1/2kT 3/2kT 5/2kT 6/2kT
Выберите верное утверждение: В смеси газов, содержащей молекулы разного сорта, будут одинаковыми…	A) средняя скорость молекул; B) импульс молекул; C) температура; D) давление
При комнатной температуре отношение молярных теплоемкостей при постоянном давлении и постоянном объеме равно для …	гелия водяного пара воздуха кислорода
В соответствии с законом равномерного распределения энергии по степеням свободы средняя кинетическая энергия молекулы идеального газа при температуре T равна: . Здесь , где , и – число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно. Для гелия ( ) число i равно …
Кинетическая энергия (в Дж) всех молекул в 2 г неона при температуре 300 К равна …
Средняя кинетическая энергия молекул газа при температуре зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место поступательное, вращательное движение молекулы как целого и колебательное движение атомов в молекуле, средняя кинетическая энергия молекулы кислорода ( ) равна …

Законы термодинамики

На рисунке изображен цикл Карно в координатах (T,S), где S-энтропия. A) Изотермическое расширение происходит на этапе… B) Адиабатное сжатие происходит на этапе… C) Адиабатное расширение происходит на этапе… D) Изотермическое сжатие происходит на этапе…	1-2 2-3 3-4 4-1
Процесс, изображенный на рисунке, в координатах (T,S), где S- энтропия, является…	изотермическим сжатием изохорным охлаждением изобарным сжатием адиабатным расширением
На (P,V) – диаграмме изображен циклический процесс. A) На участках BC-CD температура… B) На участках DA-AB температура…	A) 1. повышается 2. понижается 3. на BC – понижается, на CD – повышается 4. на BC – повышается, на CD – понижается   B) 1. повышается 2. на DA – понижается, на AB – повышается 3. на DA – повышается, на AB – понижается 4. понижается
Тепловые машины работают по циклам, представленным на рисунках. Какая из них имеет максимальный КПД при одинаковых температурах нагревателей и холодильников? ( р – давление; V– объем; на рис. Г изображен цикл Карно).	1. A; 2. Б; 3. В; 4. Г; 5. Все имеют одинаковый КПД.
Энтропия неизолированной термодинамической системы при поступлении в неё тепла в ходе обратимого процесса …	только убывает только остается постоянной только увеличивается
Двухатомному идеальному газу в результате изобарического процесса подведено количество теплоты . На увеличение внутренней энергии газа расходуется часть теплоты , равная …	0,75 0,29 0,25 0,71
В процессе обратимого изохорического охлаждения постоянной массы идеального газа его энтропия …	уменьшается увеличивается не меняется
Идеальный газ расширяясь, переходит из одного состояния в другое тремя способами: 1. изобарически; 2. изотермически; 3. адиабатически. Совершаемые в этих процессах работы соотносятся между собой следующим образом	A1>A2 >A3 A1=A2 =A3 A1>A2 <A3 A1<A2 >A3
Энтропия неизолированной термодинамической системы в процессе плавления вещества в ней …	увеличивается убывает может как убывать, так и оставаться постоянной остается постоянной
При адиабатическом сжатии идеального газа …	температура и энтропия возрастают температура не изменяется, энтропия возрастает температура возрастает, энтропия не изменяется температура возрастает, энтропия убывает
Для необратимого процесса в неизолированной термодинамической системе неравенство Клаузиуса имеет вид …
Площадь фигуры ABCD численно равна работе, совершаемой идеальным газом при изобарном расширении, на рисунке …
При изотермическом расширении давление газа растет, при этом энтропия…	увеличивается равна нулю уменьшается не изменяется
КПД цикла Карно равен 60%. Если на 20% уменьшить температуру нагревателя и на 20% увеличить температуру холодильника, КПД (в %) достигнет значения …
При плавлении вещества энтропия неизолированной термодинамической системы …	увеличивается остается постоянной убывает может как убывать, так и оставаться постоянной
В ходе необратимого процесса при поступлении в неизолированную термодинамическую систему тепла для приращения энтропии верным будет соотношение …
Если количество теплоты, получаемое рабочим телом от нагревателя, увеличится в 2 раза, то коэффициент полезного действия тепловой машины …
На рисунке изображен цикл Карно в координатах (T, S), где S – энтропия. Адиабатное сжатие происходит на этапе …
При изотермическом расширении 0,5 моля газа при температуре 200 К объем увеличился в раз ( ). Работа газа (в Дж) равна …
Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке. Работа газа за цикл (в кДж) равна …
Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке. Отношение работы газа за цикл к работе при охлаждении газа по модулю равно …
На (P,V)-диаграмме изображены 2 циклических процесса. Отношение работ , совершенных в этих циклах, равно …

Явления переноса

Явление диффузии имеет место при наличии градиента…	A) температуры B) потенциала электростатического поля; C) концентрации D) скорости слоев жидкости или газа.
Явление диффузии характеризует перенос:	A) электрического заряда; B) массы; C) энергии; D) импульса направленного движения.
Явление внутреннего трения имеет место при наличии градиента…	A) температуры; B) потенциала электростатического поля; C) концентрации; D) скорости слоев жидкости или газа.
Явление теплопроводности имеет место при наличии градиента…	A) температуры; B) потенциала электростатического поля; C) концентрации; D) скорости слоев жидкости или газа.
В жидкости вектор градиента температуры направлен вдоль оси +ОХ. В каком направлении происходит перенос тепла?	+ OZ – ОХ – OZ + ОУ + OХ
В жидкости вектор градиента скорости слоев направлен вдоль оси +ОZ. В каком направлении происходит перенос импульса молекул?	+ OZ – ОХ – OZ + ОУ + OХ

На рис. приведена фазовая диаграмма состояния воды. A) Какой процесс содержит переход «жидкость- тв. тело»? B) Какой процесс содержит переходы «жидкость- газ»?	1) Х-Х 2) М-М 3) Z-Z 4) Y-Y 5) N-N
Укажите, какие вещества имеют температуру плавления	1. полиэтилен; 2. поваренная соль; 3. смола; 4. сливочное масло; 5. стекло.
Выберите неверное утверждение: Металл отличается от диэлектрика тем, что …	1. имеет хорошую теплопроводность; 2. имеет хорошую электропроводность; 3. при Т=0 К электроны в диэлектрике находятся на самом низком энергетическом уровне, а в металле распределены по всем энергетическим уровням согласно статистике Ферми-Дирака; 4. энергетический спектр электронов в металлах не имеет запрещенной зоны; 5. даже при низких Т металл имеет свободные электроны, которые участвуют в проводимости.
Выберите верное утверждение.	Электрическое сопротивление металлов при увеличении температуры: А) Увеличивается из-за увеличения скорости хаотического движения электронов. Б) Уменьшается из-за увеличения скорости хаотического движения электронов. В) Увеличивается из-за увеличения амплитуды колебаний положительных ионов кристаллической решетки. Г) Уменьшается из-за увеличения амплитуды колебаний положительных ионов кристаллической решетки. Д) Уменьшается из-за увеличения концентрации свободных носителей электрического заряда.

Дата добавления: 2015-11-05; просмотров: 2677 | Нарушение авторских прав | Изречения для студентов

Читайте также:

Рекомендуемый контект:

Поиск на сайте:

© 2015-2021 lektsii.org – Контакты – Последнее добавление

Источник