В сосуде разделенном подвижным поршнем массой m и площадью
Рассмотрим теперь единый подход к решению задач на расчет периода различных видов колебаний.
Например, колебания совершают различные маятники, струны музыкальных инструментов, молекулы газа в звуковых волнах и молекулы жидкости в морских волнах. Колебания совершают атомы в твердых телах и электроны, входящие в состав атомов. Колебания заряда и тока происходят в колебательных контурах радиоприемников и телевизоров. По таким же законам происходят изменения напряженности электрического поля и индукции магнитного поля в электромагнитной волне.
Главное заключается в том, что все эти различные физические явления описываются одинаковыми математическими уравнениями, то есть подчиняются одинаковым законам.
Рассмотрим решения задач на различные виды свободных колебаний. Потери энергии в таких колебательных системах пренебрежимо малы.
- В механике.
Задача 1. Шарик присоединен к двум пружинам так, как изображено на рисунке. Масса шарика равна m, жесткость одной пружины равна k, жесткость другой – 3k. Определите период малых колебаний шарика T.
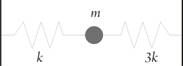
Рис. 1.
Если шарик сдвинуть на расстояние x от положения равновесия, то согласно второму закону Ньютона m a = – k x – 3 k x = – 4 k x, откуда находим a = – ( 4 k / m ) x или x″= – (4 k/m) x.
Сравнивая это уравнение с уравнением колебаний x″ = – ω2 x, получаем:
Период колебаний:
- В молекулярной физике.
Задача 2. В сосуде, разделенном подвижным поршнем массой m и площадью поперечного сечения S, находится идеальный газ. Когда поршень расположен ровно посередине сосуда, давление газа в каждой половине p, объем половины сосуда равен V. Определите период малых колебаний поршня, считая процесс колебаний изотермическим, трением пренебречь.
Объем каждой из частей , ,
значит,
откуда получаем значение силы
Так как ∆ х < V / S, то
Согласно второму закону Ньютона получим:
где а – ускорение поршня.
т. е. х ´´ ~ – x , а это значит, что «х» изменяется по законам синуса или косинуса и
a = x “ = – ω0 2 x. Поэтому
Рис. 3.
- В электростатике.
Задача 3. Шарик массой m = 20 г подвешен на шелковой нити длиной l = 10 см. Шарик имеет положительный заряд q = + 10–5 Кл и находится в однородном электрическом поле напряженностью Е = 104 В / м, направленном вертикально вниз. Каков период малых колебаний шарика?
Отведем заряженный шарик, находящийся в электрическом поле на малый угол α. Показываем силы на него действующие.Применяем второй закон Ньютона, учитывая, что сила, возвращающая заряженный шарик в положение равновесия и угол отклонения шарика из положения равновесия имеют противоположное направление – это означает знак «–».
Задача 4. Колебательный контур, состоящий из конденсатора емкостью С и катушки индуктивностью L, подключен через ключ К к источнику с постоянной ЭДС ε и внутренним сопротивлением r (рис. 5).
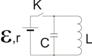Рис. 5.
Ключ замыкают, а после того как устанавливается постоянный режим, размыкают его. Найти зависимость напряжения на конденсаторе от времени после размыкания ключа. Омическим сопротивлением катушки пренебречь.
При замкнутом ключе через катушку течет постоянный ток I = ε / r. Напряжение на конденсаторе и заряд на нем равны нулю, так как напряжение на конденсаторе равно напряжению на катушке, а оно, при отсутствии активного сопротивления катушки, равно нулю. Из начальных условий t = 0 u = 0 и i = ε / r следует, что напряжение на конденсаторе в зависимости от времени изменяется по закону синуса
После размыкания ключа в колебательном контуре начнутся свободные электромагнитные колебания. Пусть в некоторый момент времени заряд на конденсаторе q, а напряжение на конденсаторе равно u. Напряжение на катушке будет тоже u.
Это означает, что напряжение изменяется по гармоническому закону, а уравнение
, а амплитуда напряжения
Зависимость напряжения на конденсаторе от времени после размыкания ключа имеет вид
Задачи для самостоятельного решения.
1. Шарик массой m = 20 г, подвешен на шелковой нити и помещен над положительно заряженной плоскостью, создающей вертикальное однородное электрическое поле напряженностью. Шарик имеет положительный заряд Кл. Период малых колебаний шарика Т = 1 с. Чему равна длина нити?
2. При отклонении из положения равновесия ареометр в сосуде с водой совершает гармонические колебания с периодом 1 с. Каков будет период колебаний ареометра в керосине? Сопротивлением среды пренебречь. (1, 12 с )
3. Маятник с периодом колебаний 1 с представляет собой шарик массой 16 г, подвешенный на нити, не проводящей электричество. Шарик электризуют отрицательным зарядом и помещают в электрическое поле, Период колебаний маятника Т1 = 0, 95 с. Вычислить напряженность электрического поля, если заряд на шарике равен Кл. (В/м )
4. В колебательном контуре, состоящем из катушки индуктивности и воздушного конденсатора, величина тока меняется со временем по гармоническому закону: i = I м cos ω t . Когда ток контуре оказывается равным нулю, в пространство между пластинами конденсатора быстро вводят диэлектрическую пластину с диэлектрической проницаемостью ε. Время этого внешнего воздействия мало по сравнению с периодом колебаний в контуре. Найдите зависимость тока в контуре от времени после внесения пластины.
Такой подход к обучению поможет обучающимся быть более уверенными в себе при решении задач на нахождение периода гармонических колебаний. Эта информация обеспечит понимание применения метода аналогий в решении задач на различные виды колебаний.
Литература
- Лабковский, В.Б. 220 задач по физике с решениями: кн. для учащихся 10 –11 кл. общеобразоват. учреждений / В.Б. Лабковский. – М. : Просвещение, 2006. –256 с. :ил. – (Задачник).
- Гомонова, А.И., Плетюшкин, В.А., Погожев В.А. Задачи по физике. Пособие для учащихся 9-11 классов. – М.: Экзамен (Серия «Экзамен»), 1998. – 192 с.
- Панов, Н.А., Шабунин, С.А., Тихонин, Ф.Ф. Единый государственный экзамен. Физика. Типовые тестовые задания: Учебно-практическое пособие / Н.А. Панов, С.А. Шабунин, Ф.Ф. Тихонин. – М.: Издательство «Экзамен», 2003. – 56 с.
- Орлов, В.А., Никифоров, Г.Г., Ханнанов, Н.К. Учебно-тренировочные материалы для подготовки к единому государственному экзамену. Физика / Орлов В.А., Никифоров Г.Г., Ханнанов Н.К. – М.: Интеллект-Центр, 2005 –248 с.
Источник
МОУ Лицей «Технико-экономический»
г. Новороссийска Краснодарского края
Решение задач уровня C ЕГЭ
по теме
«Гармонические колебания»
с применением формулы периода колебаний пружинного маятника и нахождением возвращающей квазиупругой силы и соответствующего условию коэффициента k этой силы
Вашему вниманию предлагаются решения задач уровня С4 КИМов ЕГЭ по физике на различные типы малых колебаний (ареометра, поршня в цилиндре с газом, заряженной бусинки между двумя зарядами), которые можно свести к гармоническим колебаниям. Подробные решения с поясняющими характер движения рисунками позволяют выработать у учащихся алгоритм решения подобных задач. Данный тип задач решаю на уроках в 10 и 11 классах, а также с группой одаренных детей с целью подготовки к олимпиадам после 9 класса.
Учитель высшей категории
Жукова Людмила Николаевна
С1. Ареометр, погруженный в жидкость, совершает вертикальные гармонические колебания с малой амплитудой. Найдите период этих колебаний. Масса ареометра равна 40г, радиус его трубки 2 мм, плотность жидкости 0,8 г/см3. Сопротивлением жидкости можно пренебречь.
Решение:
Период гармонических колебаний пружинного маятника:
,
при этом на маятник действует упругая возвращающая сила:
На ареометр, смещенный от положения равновесия на расстояние x, действует избыточная архимедова сила ΔFA = g ΔV, где ΔV = S x – дополнительный объем вытесненной воды при смещении ареометра.
ΔFA = ρж g S x,
где S = – площадь сечения трубки ареометра. Архимедова сила является в данном случае возвращающей, «квазиупругой» силой:
,
где k – коэффициент возвращающей силы.
,
Период колебаний ареометра:
C2. В сосуде, разделенном подвижным поршнем массой m и площадью поперечного сечения S, находится идеальный газ. Когда поршень расположен ровно посередине сосуда, давление газа в каждой половине p, объем половины сосуда равен V. Определите период T малых колебаний поршня, считая процесс колебаний изотермическим, трением пренебречь.
Решение:
Сместим поршень относительно положения равновесия на малое расстояние x, при этом объем левой части сосуда уменьшился на ΔV = S x и стал V1 = V – S x; правой части – увеличился: V2 = V + S x.
Давление в левой части – p1, в правой – p2.
На поршень действует возвращающая сила за счет разности давлений:
,
которая является «квазиупругой»: , где k –коэффициент возвращающей силы.
Считая колебания поршня гармоническими, период его колебаний:
Найдем коэффициент k:
Т.к. процесс изотермический, то по закону Бойля-Мариотта: для газа в левой и правой частях сосуда:
;
;
;
Т.к. x – мало, выражением S2x2 можно пренебречь и возвращающая сила:
но
Период колебаний поршня:
C3. Бусинка массы m и заряда Q совершает малые колебания между 2-х зарядов по q каждый, расстояние между которыми 2L. Как изменится заряд бусинки при увеличении частоты малых колебаний бусинки в 2 раза.
;
Решение:
При выведении заряда Q из положения равновесия на величину x на него начинают действовать кулоновские силы
причем , поэтому на Q действует возвращающая, «квазиупругая» сила
, пропорциональная смещению x
Т.к. бусинка совершает малые колебания, величиной x в знаменателе можно пренебречь:
С другой стороны: возвращающая сила пропорциональна деформации:
Из и следует:
- коэффициент «квазиупругой» силы
Считая колебания бусинки гармоническими, период колебаний будем определять по формуле:
Частота:
Ответ: увеличится в 4 раза
Источник
1. Воздушный шар объемом 2500 м3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. До какой минимальной температуры нужно нагреть воздух в шаре, чтобы шар взлетел вместе с грузом (корзиной и воздухоплавателем) массой 200 кг? Температура окружающего воздуха 7°С, его плотность 1,2 кг/м3. Оболочку шара считать нерастяжимой. (Решение)
2. Воздушный шар объемом 2500 м3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Рассчитайте максимальную массу груза, который может поднять шар, если воздух в нем нагреть до температуры 77°С. Температура окружающего воздуха 7°С, его плотность 1,2 кг/м3. Оболочку шара считать нерастяжимой. (Решение)
3.
Воздушный шар объемом 2500 м3 имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Если температура окружающего воздуха 7°С, а его плотность 1,2 кг/м3, то при нагревании воздуха в шаре до температуры 77°С шар поднимает груз с максимальной массой 200 кг. Какова масса оболочки шара? Оболочку шара считать нерастяжимой. (Решение)
4.
Воздушный шар имеет газонепроницаемую оболочку массой 400 кг и содержит 100 кг гелия. Какой груз он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па? Считать, что оболочка шара не оказывает сопротивления изменению объема шара. (Решение)
5.
Воздушный шар с газонепроницаемой оболочкой массой 400 кг заполнен гелием. Он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па, груз массой 225 кг. Какова масса гелия в оболочке шара? Считать, что оболочка шара не оказывает сопротивления изменению объема шара. (Решение)
6. При исследовании уравнения состояния газа ученик соединил сосуд (1) объемом 150 мл с манометром (2) тонкой трубкой и опустил сосуд в горячую воду (см. рисунок). Чему равна плотность воздуха в сосуде? Начальные показания манометра равны 0 мм рт. ст. Шкала манометра и нижняя шкала барометра (3) проградуированы в мм рт. ст. Верхняя шкала барометра проградуирована в кПа. Объем измерительного механизма манометра и соединительной трубки значительно меньше 150 мл. (Решение)
7. Теплоизолированный сосуд объемом V = 2 м3 разделен пористой неподвижной перегородкой на две равные части. Атомы гелия могут свободно проникать через поры в перегородке, а атомы аргона — нет. В начальный момент в одной части сосуда находится νHe = 2 моль гелия, а в другой — νAr = 1 моль аргона. Температура гелия TНe = 300 К, а температура аргона ТAr = 600 К. Определите температуру гелия после установления равновесия в системе. (Решение)
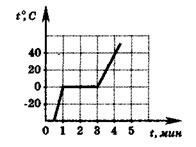8. На рисунке представлен график изменения температуры вещества в калориметре с течением времени. Теплоемкостью калориметра и тепловыми потерями можно пренебречь и считать, что подводимая к сосуду мощность постоянна. Рассчитайте удельную теплоемкость вещества в жидком состоянии. Удельная теплота плавления вещества равна 100 кДж/кг. В начальный момент времени вещество находилось в твердом состоянии. (Решение)
9. В цилиндрическом сосуде под поршнем длительное время находятся вода
и ее пар. Поршень начинают вдвигать в сосуд. При этом температура
воды и пара остается неизменной. Как будет меняться при этом масса
пара в сосуде? Ответ поясните.
(Решение)
10. В цилиндрическом сосуде под поршнем длительное время находятся вода
и ее пар. Поршень начинают вдвигать в сосуд. При этом температура
воды и пара остается неизменной. Как будет меняться при этом
отношение массы пара к массе жидкости в сосуде? Ответ поясните. (Решение)
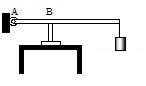11. В цилиндр объемом 0,5 м3 насосом закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии стержнем, который может свободно поворачиваться вокруг оси в точке А (см. рисунок). К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через 580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Площадь закрытого клапаном отверстия 5·10-4 м2, расстояние АВ равно 0,1 м. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите длину стержня, если его можно считать невесомым.
(Решение)
12. В цилиндр объемом 0,5 м3 насосом закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии стержнем, который может свободно поворачиваться вокруг оси в точке А (см. рисунок к зад. 11). К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через 580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Площадь закрытого клапаном отверстия 5·10-4 м2, расстояние АВ равно 0,1 м. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите длину AB. (Решение)
13. Воздушный шар имеет газонепроницаемую оболочку массой 400 кг и содержит 100 кг гелия. Какой груз он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па? Считать, что оболочка шара не оказывает сопротивления изменению объема шара.
(Решение)
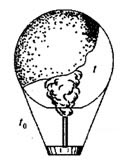
14. Воздушный шар, оболочка которого имеет массу М = 145 кг и объем V = 230 м3, наполняется горячим воздухом при нормальном атмосферном давлении и температуре окружающего воздуха t0 = 0°C. Какую минимальную температуру t должен иметь воздух внутри оболочки, чтобы шар начал подниматься? Оболочка шара нерастяжима и имеет в нижней части небольшое отверстие.
(Решение)
15. В высоком вертикальном цилиндрическом сосуде под тяжелым поршнем, способным перемещаться вдоль стенок сосуда практически без трения, находится некоторое количество воздуха под давлением p = 1,5 атм. Поршень находится в равновесии на высоте H1 = 20 см над дном сосуда. Определите, на какое расстояние ΔH сместится поршень, если сосуд перевернуть открытым концом вниз и дождаться установления равновесия. Считать температуру воздуха и атмосферное давление p0 = 1 атм постоянными. Массой воздуха в сосуде по сравнению с массой поршня можно пренебречь.
(Решение)
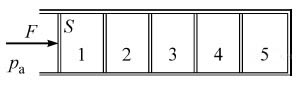16. Горизонтальный хорошо теплопроводящий цилиндр, разделённый подвижными поршнями площадью S = 100 см2 на 5 отсеков (№№ 1—5), содержит в них одинаковые количества идеального газа при температуре окружающей среды и под давлениями, равными давлению pа = 105 Па окружающей цилиндр атмосферы (см. рисунок). Каждый поршень сдвигается с места, если приложенная к нему горизонтальная сила превышает силу сухого трения Fтр = 2 Н. К самому левому поршню прикладывают горизонтальную силу F, медленно увеличивая её по модулю. Какого значения достигнет F, когда объём газа в самом правом, 5-м отсеке цилиндра уменьшится в n = 2 раза? Процессы изменения состояния газов в отсеках цилиндра считать изотермическими.
(Решение)
17. Горизонтальный хорошо теплопроводящий цилиндр, разделённый подвижными поршнями площадью S = 50 см2 на 5 отсеков (№№ 1—5), содержит в них одинаковые количества идеального газа при температуре окружающей среды и под давлениями, равными давлению pа = 105 Па окружающей цилиндр атмосферы (см. рисунок к зад 16). Каждый поршень сдвигается с места, если приложенная к нему горизонтальная сила превышает силу сухого трения Fтр = 4 Н. К самому левому поршню прикладывают горизонтальную силу F, медленно увеличивая её по модулю. Когда давление газа в самом правом, пятом отсеке цилиндра, увеличится в n = 3 раза? Процессы изменения состояния газов в отсеках цилиндра считать изотермическими.
(Решение)
18. Газ в цилиндрическом сосуде разделен на две равные части подвижным поршнем, имеющим массу m и площадь сечения S. При горизонтальном положении цилиндра давление газа в каждой половине сосуда равно p. Определить давление p1 газа над поршнем при вертикальном положении цилиндра. Температуру газа считать постоянной.
(Решение)
19. Сферическую оболочку воздушного шара делают из материала, квадратный метр которого имеет массу 1 кг. Шар наполняют гелием при атмосферном давлении 105 Па. Определите минимальную массу оболочки, при которой шар начнет поднимать сам себя. Температура гелия и окружающего воздуха одинакова и равна 0°С. (Площадь сферы S= 4πr2, объем шара V = 4/3πr3.)
(Решение)
20. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Площадь поперечного сечения поршня S = 30 см2. Давление окружающего воздуха p = 105 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. Какое количество теплоты нужно отвести от газа при его медленном охлаждении, чтобы поршень передвинулся на расстояние х = 10 см?
(Решение)
21. В горизонтальном цилиндрическом сосуде, закрытом подвижным поршнем, находится одноатомный идеальный газ. Давление окружающего воздуха р = 105 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. В процессе медленного охлаждения от газа отведено количество теплоты |Q| = 75 Дж. При этом поршень передвинулся на расстояние х = 10 см. Чему равна площадь поперечного сечения поршня?
(Решение)
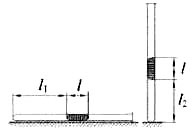22. В запаянной с одного конца длинной горизонтальной стеклянной трубке постоянного сечения (см. рисунок) находится столбик воздуха длиной l1 = 30,7 см, запертый столбиком ртути. Если трубку поставить вертикально отверстием вверх, то длина воздушного столбика под ртутью будет равна l2 = 23.8 см. Какова длина ртутного столбика? Атмосферное давление 747 мм рт. ст.
(Решение)
23. В водонепроницаемым мешок, лежащий на дне моря на глубине 73,1 м. закачивается сверху воздух. Вода вытесняется из мешка через нижнее отверстие, и. когда объём воздуха в мешке достигает 28,0 м, мешок всплывает вместе с прикреплённым к нему грузом массой 25,0 тонн. Определите массу воздуха в мешке в момент начала его всплывания. Температура воды раина 7°С. атмосферное давление па уровне моря равно 105 Па. Объёмом груза и стенок мешка пренебречь. Масса оболочки мешка неизвестна.
(Решение)
24. Сосуд разделен тонкой перегородкой на две части, отношение объёмов у которых V2/V1 = 3. В первой и второй частях сосуда находится воздух с относительной влажностью соответственно φ1 = 60% и φ2 = 70%. Какой будет влажность воздуха в сосуде, если перегородку убрать? Считать, что температура воздуха постоянна.(Решение)
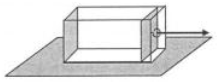25. В металлическом сосуде под поршнем находится воздух при атмосферном давлении (см. рисунок). Сосуд имеет массу 10 кг и расположен в горизонтальном положении на поверхности стола. Поршень может скользить без трения со стенками сосуда. Массон поршня и воздуха, заключённого в сосуде, можно пренебречь. За привязанный к нему шнур поршень очень медленно тянут в горизонтальном направлении. На сколько процентов возрастёт объём воздуха под поршнем к моменту, когда сосуд начнёт скользить по столу? Коэффициент трения покоя между сосудом и поверхностью стола равен 0,5. Площадь дна поршня 105 см2. Атмосферное давление 105 Па.
(Решение)
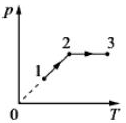26.Один моль одноатомного идеального газа совершает процесс 1-2-3, график которого показан на рисунке в координатах р-Т. Известно, что давление газа р в процессе 1-2 увеличилось в 2 раза. Какое количество теплоты было сообщено газу в процессе 1-2-3, если его температура Т в состоянии 1 равна 300 К, а в состоянии 3 равна 900 К?
(Решение)
27. Теплоизолированный цилиндр разделён подвижным теплопроводящим поршнем на две части. В одной части цилиндра находится гелий, а в другой – аргон. В начальный момент температура гелия равна 300 К,. а аргона – 900 К. Объёмы, занимаемые газами, одинаковы, а поршень находится в равновесии. Во сколько раз изменится объём, занимаемый гелием, после установления теплового равновесия, если поршень перемешается без трения? Теплоёмкостью цилиндра н поршня пренебречь.
(Решение)
Источник