В сосуде с водой находится капиллярная стеклянная трубка
>>> Перейти на мобильный размер сайта >>>
Учебник для 10 класса
ФИЗИКА
Задачи на материал данной главы отличаются от обычных задач на гидростатику лишь тем, что в них принимается во внимание еще одна сила — сила поверхностного натяжения, определяемая формулой (7.4.3).
Для решения задач используются также формулы для поверхностной энергии (7.3.2), давления под изогнутой поверхностью (7.6.6) и высоты поднятия жидкости в капилляре (7.7.3).
Задача 1
Определите энергию, освободившуюся при слиянии мелких капель воды радиусом r = 2 • 10-3 мм в одну большую каплю радиусом R = 2 мм. Считать, что при слиянии мелких капель температура не изменяется. Поверхностное натяжение воды равно σ = 7,4 • 10-2 Н/м.
Решение. Обозначим число мелких капель через n. Тогда общая поверхность всех мелких капель
Поверхность одной большой капли
Поверхностная энергия всех мелких капель
а одной крупной капли
Так как температура не изменялась, то кинетическая энергия молекул воды тоже не изменилась. Следовательно, выделение энергии произошло за счет уменьшения потенциальной (поверхностной)энергии:
Чтобы найти число капель п, учтем, что объем воды не изменился. Сумма объемов мелких капель
а объем большой капли
Так как V1 = V2, то
Отсюда число мелких капель
Подставляя это значение n в выражение (7.8.1), получим
Задача 2
Смачиваемый водой кубик массой m = 0,02 кг плавает на поверхности воды. Ребро кубика имеет длину а = 0,03 м. На каком расстоянии х от поверхности воды находится нижняя грань кубика?
Решение. Архимедова сила уравновешивает силу тяжести кубика и силу поверхностного натяжения. Следовательно,
Отсюда
Силы поверхностного натяжения вносят поправку около 1 мм.
Задача 3
Два мыльных пузыря радиусами R и r «срослись», как показано на рисунке 7.29. Какую форму примет пленка, разделяющая оба пузыря? Какие углы образуются между пленками в местах их соприкосновения?

Рис. 7.29
Решение. Давление внутри мыльного пузыря радиусом R больше атмосферного давления на величину , а внутри меньшего пузыря — на величину . В этих выражениях учтено, что у мыльного пузыря две поверхности. Давление внутри пузыря радиусом R вместе с давлением участка пленки между пузырями должно уравновесить давление внутри меньшего пузыря. Следовательно,
где Rx — радиус кривизны участка пленки АВ. Отсюда
Силы поверхностного натяжения в любой точке поверхности соприкосновения пузырей уравновешивают друг друга и равны между собой. А это возможно только в том случае, когда углы между векторами сил равны 120°.
Задача 4
Длинную стеклянную капиллярную трубку, радиус канала которой r = 1 мм, закрыли снизу и наполнили водой. Трубку поставили вертикально и открыли ее нижний конец, при этом часть воды вылилась. Какова высота столба оставшейся в капилляре воды?
Решение. Столб воды в поставленной вертикально трубке удерживается верхним и нижним менисками (рис. 7.30).
Рис. 7.30
Давление в точке В под верхним мениском
а давление в точке С над нижним мениском
С другой стороны,
Следовательно,
или
Отсюда
Задача 5
Конец капиллярной трубки опущен в воду. Какое количество теплоты Q выделится при поднятии жидкости по капилляру? Краевой угол принять равным нулю (полное смачивание).
Решение. Жидкость поднимается согласно формуле (7.7.3) на высоту h = . Потенциальная энергия столбика жидкости в поле тяготения Земли
так как
Силы поверхностного натяжения совершают работу
На увеличение потенциальной энергии Еp идет половина этой работы. Следовательно, выделение теплоты происходит за счет другой половины. Таким образом,
Задача 6
Капиллярная трубка погружена в воду таким образом, что длина непогруженной ее части составляет l = 0,2 м. Вода поднялась в трубке на высоту = 0,1 м. В этом положении верхний конец трубки закрывают пальцем и трубку погружают в воду до тех пор, пока уровень воды в ней не сравняется с уровнем воды в сосуде. Найдите длину выступающей из воды части трубки в этом положении. Внешнее давление р0 = 105 Па.
Решение. Согласно формуле (7.7.3)
Найдем давление воздуха, которое установится в погруженном закрытом сверху капилляре после выравнивания уровней воды (в сосуде и капилляре). Обозначим давление воздуха в капилляре буквой р, тогда под вогнутой поверхностью воды в капилляре давление равно (см. § 7.6). Так как жидкость в капилляре и сосуде находится в равновесии, то давление на жидкость в сосуде (атмосферное давление р0) равно давлению :
Откуда
Полагая температуру неизменной и применив закон Бойля—Мариотта, получим
Отсюда
Найдем из уравнения (7.8.7) значение σ и подставим его в выражение (7.8.8):
И наконец, подставив в (7.8.10) выражение (7.8.11) для р, окончательно получим
Упражнение 6
- Какую работу надо совершить, чтобы выдуть мыльный пузырь диаметром D = 12 см? Поверхностное натяжение мыльного раствора считать равным 4 • 10-2 Н/м.
- Каким усилием можно оторвать тонкое металлическое кольцо от мыльного раствора (σ = 4 • 10-2 Н/м), если диаметр кольца 15,6 см, масса 7,0 г и кольцо соприкасается с раствором по окружности?
- Каким образом, используя явления смачивания и несмачивания, можно осуществить минимальный и максимальный термометры?
- При удалении с поверхности ткани жирного пятна рекомендуется смачивать пропитанной бензином ваткой края пятна. Смачивать бензином сразу само пятно не следует. Почему?
- Чтобы мазь лучше впитывалась в смазанные лыжные ботинки, их нагревают. Как нужно нагревать ботинки — снаружи или изнутри?
- Почему с помощью утюга можно вывести пятно жира с костюма?
- Почему при сушке дров на солнце на конце полена, находящемся в тени, выступают капельки воды?
- На сколько давление воздуха внутри мыльного пузыря больше атмосферного давления, если диаметр пузыря D = 10 мм? Поверхностное натяжение мыльного раствора σ = 4 • 10-2 Н/м.
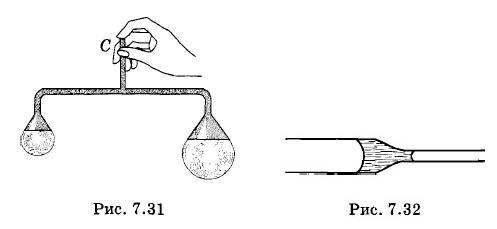
- Из трубки с раструбами на концах выдули два мыльных пузыря (рис. 7.31), после чего закрыли пальцем трубку С. Будет ли воздух переходить из одного пузыря в другой? До каких пор?

Рис. 7.31
- В носик стеклянной трубки от пипетки (рис. 7.32) попадает капля воды. В какую сторону при этом устремляется капля — к широкому или узкому концу трубки? Почему?
Рис. 7.32
- В дне чайника имеется круглое отверстие диаметром 0,1 мм. До какой высоты можно налить воду в чайник, чтобы она не выливалась через отверстие? Сохранится ли это условие, если воду в чайнике нагревать?
- Конец стеклянной капиллярной трубки радиусом r = 0,05 см опущен в воду на глубину h = 2 см. Какое давление необходимо, чтобы выдуть пузырек воздуха через нижний конец трубки?
- Смачивающая жидкость плотностью р поднялась в капиллярной трубке на высоту h. Каково давление в жидкости внутри капилляра на высоте h/4? Атмосферное давление равно р0.
- Докажите, что в случае неполного смачивания (Θ ≠ 0) высота поднятия жидкости в вертикальной капиллярной трубке вычисляется по формуле , где Θ — краевой угол, r — радиус канала трубки и ρ — плотность жидкости. Как изменится формула , если сосуд с жидкостью будет установлен в лифте, движущемся с ускорением , направленным вверх? вниз?
- Длинную капиллярную трубку радиусом 0,8 мм заполнили водой и перевели в вертикальное положение. Найдите массу жидкости, оставшейся в трубке после того, как часть воды вылилась.
- В капиллярной трубке, опущенной вертикально в воду на глубину l, вода поднялась на высоту h (рис. 7.33). Нижний конец трубки закрывают, вынимают ее из воды и снова открывают. Определите длину столбика воды, оставшейся в трубке.

Рис. 7.33
- Стеклянная капиллярная трубка, внутренний диаметр которой d = 0,5 мм, погружена в воду. Верхний конец трубки выступает на h = 2 см над поверхностью воды. Какую форму имеет мениск? Чему равен его радиус кривизны?
- Капиллярная стеклянная трубка имеет радиус канала r = 0,05 см и запаяна сверху. Трубка открытым концом опускается вертикально в воду. Какой длины следовало бы взять трубку, чтобы при этих условиях вода в ней поднялась на высоту h = 1 см? Давление воздуха р0 = 105 Па. Поверхностное натяжение воды σ = 7 • 10-2 Н/м.
- Каким образом можно без потерь налить жидкость в сосуд, находясь в условиях невесомости (на космическом корабле)? Как в этих условиях извлечь жидкость из сосуда?
- Великому датскому физику Н. Бору довелось однажды мыть посуду в горной альпийской хижине. Он был крайне удивлен, увидев, что можно получить чистую посуду с помощью небольшого количества грязной воды и грязной тряпки. В чем здесь дело?
Источник
Глава 7. Поверхностное натяжение в жидкостях
1. Какую работу надо совершить, чтобы выдуть мыльный пузырь диаметром D = 12 см? Поверхностное натяжение мыльного раствора считать равным 4 • 10-2 Н/м.
2. Каким усилием можно оторвать тонкое металлическое кольцо от мыльного раствора (σ = 4 • 10-2 Н/м), если диаметр кольца 15,6 см, масса 7,0 г и кольцо соприкасается с раствором по окружности?
3. Каким образом, используя явления смачивания и несмачивания, можно осуществить минимальный и максимальный термометры?
4. При удалении с поверхности ткани жирного пятна рекомендуется смачивать пропитанной бензином ваткой края пятна. Смачивать бензином сразу само пятно не следует. Почему?
5. Чтобы мазь лучше впитывалась в смазанные лыжные ботинки, их нагревают. Как нужно нагревать ботинки — снаружи или изнутри?
6. Почему с помощью утюга можно вывести пятно жира с костюма?
7. Почему при сушке дров на солнце на конце полена, находящемся в тени, выступают капельки воды?
8. На сколько давление воздуха внутри мыльного пузыря больше атмосферного давления, если диаметр пузыря D = 10 мм? Поверхностное натяжение мыльного раствора σ = 4 • 10-2 Н/м.
9. Из трубки с раструбами на концах выдули два мыльных пузыря (рис. 7.31), после чего закрыли пальцем трубку С. Будет ли воздух переходить из одного пузыря в другой? До каких пор?
10. В носик стеклянной трубки от пипетки (рис. 7.32) попадает капля воды. В какую сторону при этом устремляется капля — к широкому или узкому концу трубки? Почему?
11. В дне чайника имеется круглое отверстие диаметром 0,1 мм. До какой высоты можно налить воду в чайник, чтобы она не выливалась через отверстие? Сохранится ли это условие, если воду в чайнике нагревать?
12. Конец стеклянной капиллярной трубки радиусом r = 0,05 см опущен в воду на глубину h = 2 см. Какое давление необходимо, чтобы выдуть пузырек воздуха через нижний конец трубки?
13. Смачивающая жидкость плотностью р поднялась в капиллярной трубке на высоту h. Каково давление в жидкости внутри капилляра на высоте h/4? Атмосферное давление равно р0.
14. Докажите, что в случае неполного смачивания высота поднятия жидкости в вертикальной капиллярной трубке вычисляется по формуле где — краевой угол, r — радиус канала трубки и ρ — плотность жидкости. Как изменится формула если сосуд с жидкостью будет установлен в лифте, движущемся с ускорением направленным вверх? вниз?
15. Длинную капиллярную трубку радиусом 0,8 мм заполнили водой и перевели в вертикальное положение. Найдите массу жидкости, оставшейся в трубке после того, как часть воды вылилась.
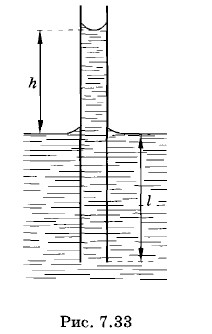
16. В капиллярной трубке, опущенной вертикально в воду на глубину l, вода поднялась на высоту h (рис. 7.33). Нижний конец трубки закрывают, вынимают ее из воды и снова открывают. Определите длину столбика воды, оставшейся в трубке.
17. Стеклянная капиллярная трубка, внутренний диаметр которой d = 0,5 мм, погружена в воду. Верхний конец трубки выступает на h = 2 см над поверхностью воды. Какую форму имеет мениск? Чему равен его радиус кривизны?
18. Капиллярная стеклянная трубка имеет радиус канала r = 0,05 см и запаяна сверху. Трубка открытым концом опускается вертикально в воду. Какой длины следовало бы взять трубку, чтобы при этих условиях вода в ней поднялась на высоту h = 1 см? Давление воздуха р0 = 105 Па. Поверхностное натяжение воды σ = 7 • 10-2 Н/м.
19. Каким образом можно без потерь налить жидкость в сосуд, находясь в условиях невесомости (на космическом корабле)? Как в этих условиях извлечь жидкость из сосуда?
20. Великому датскому физику Н. Бору довелось однажды мыть посуду в горной альпийской хижине. Он был крайне удивлен, увидев, что можно получить чистую посуду с помощью небольшого количества грязной воды и грязной тряпки. В чем здесь дело?
Источник
Можаев В. Задачи с жидкостями //Квант. — 2006. — № 1. — С. 40-43.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
В этой статье будут рассмотрены задачи, в которых жидкость, с одной стороны, является средой, где находятся твердые тела, а с другой стороны, она, как жидкий элемент, участвует в движении, подобно твердому телу. Наиболее сложными являются комбинированные задачи, в которых жидкость движется вместе с находящимся в ней твердым телом (например, разобранная ниже задача 6).
Перейдем к обсуждению конкретных задач.
Задача 1. В цилиндрический сосуд с водой опустили кусок льда, в который вморожен осколок стекла. При этом уровень воды в сосуде поднялся на h = 11 мм, а лед остался на плаву, целиком погрузившись в воду. На сколько опустится уровень воды в сосуде после того, как весь лед растает? Плотность воды ρв = 1 г/см3, плотность льда ρл = 0,9 г/см3, стекла ρст = 2,0 г/см3
Обозначим первоначальный объем льда через Vл, а объем стекла — через Vст. Когда кусок льда полностью погрузился в воду, он вытеснил объем воды, равный
Очевидно, что этот же объем равен
где S — площадь поперечного сечения сосуда.
Теперь запишем условие плавания куска льда с вмороженным осколком стекла — суммарная сила тяжести льда и стекла равна выталкивающей силе:
Из совместного решения полученных уравнений найдем объемы льда и стекла:
Из растаявшего льда образовалась вода объемом
Поскольку кусок стекла остается в воде, понижение уровня воды в сосуде за время таяния льда будет равно
Задача 2. В вертикально расположенной трубке — с открытым верхним концом, с постоянным внутренним сечением и длиной 3L = 1080 мм — столбиком ртути длиной L заперт слой воздуха такой же длины. Какой длины столб ртути останется в трубке, если ее перевернуть открытым концом вниз? Внешнее давление p0 = 774 мм рт. ст.
Обозначим давление воздуха под ртутным столбиком в исходном положении трубки через p1. Тогда условие равновесия столбика ртути длиной L запишется в виде
где ρ – плотность ртути. Предположим, что после переворота трубки и установления первоначальной температуры часть ртути выльется. Обозначим через h длину столбика оставшейся в трубке ртути. Новое условие равновесия будет иметь вид
где p2 – новое давление воздуха над ртутным столбиком.
Условие сохранения количества изолированного воздуха позволяет записать
Подставляя сюда p1 из первого равенства, а p2 – из второго, получим уравнение относительно h:
или, если записать атмосферное давление в виде , где H0 = 774 мм:
Для данных численных значений L и H0 (в мм) получается, что
h = 270 мм.
Задача 3. U–образная трубка расположена вертикально и заполнена жидкостью. Один конец трубки открыт в атмосферу, а другой конец соединен с сосудом объемом V0 = 0,1 л, заполненным гелием (рис. 1). Объем всей трубки равен объему этого сосуда. В некоторый момент гелий начинают медленно нагревать. Какое минимальное количество теплоты необходимо подвести к гелию, чтобы вся жидкость вылилась из трубки? Атмосферное давление p0 = 105 Па; длины трех колен трубки одинаковы; давление, создаваемое столбом жидкости в вертикальном колене, равно p0/8.
Рис. 1
Обозначим полную длину трубки через 3L, а площадь внутреннего поперечного сечения трубки – S. Поскольку объем трубки V0, то длина каждого колена
Весь процесс нагрева гелия можно разбить на три участка. Первый участок — это когда жидкость еще находится в левом вертикальном колене. Рассмотрим момент времени, когда уровень жидкости в левом колене переместился на величину z, . Из условия равновесия жидкости в трубке найдем давление гелия:
где ρж – плотность жидкости. На втором участке, для которого , давление гелия
а на третьем участке, для
На рисунке 2 изображен график зависимости давления гелия от его объема V, который связан со смещением z простым соотношением:
На первых двух участках тепло необходимо подводить к гелию — это однозначно: здесь газ, расширяясь, совершает работу и одновременно нагревается. А вот третий участок неоднозначен: здесь газ также совершает работу, но при этом он может и охлаждаться. Убедимся, что и на этом участке тепло тоже подводится.
Учитывая, что , запишем уравнение процесса для третьего участка в виде
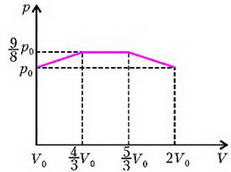
Рис. 2.
Рассмотрим малое изменение объема ΔV. Тогда работа, совершенная гелием, равна
Запишем уравнение состояния гелия как идеального газа:
где ν – количество вещества, Т – температура газа. Подставим в это уравнение выражение для давления на третьем участке процесса и получим
Продифференцируем обе части этого уравнения:
Теперь найдем изменение внутренней энергии гелия при изменении объема на ΔV:
Согласно первому началу термодинамики, подведенное количество теплоты равно сумме изменения внутренней энергии газа и совершенной им работы:
Легко убедиться, что при и
Итак, на всех участках тепло подводится, поэтому полное подведенное к гелию количество теплоты Q найдем как сумму полного изменения внутренней энергии и полной работы, которую совершил гелий:
Поскольку начальная и конечная температуры равны, соответственно,
то изменение внутренней энергии равно
Полную работу найдем как площадь под кривой на рисунке 2:
Тогда окончательно
Задача 4. «Тройник» с двумя открытыми в атмосферу вертикальными трубками и одной закрытой (горизонтальная трубка) полностью заполнен водой (рис. 3). После того, как тройник начали двигать по горизонтали в плоскости рисунка влево с некоторым постоянным ускорением, из него вылилась 1/16 массы всей воды. Чему при этом стало равно давление в жидкости у закрытого конца – в точке А? Трубки имеют одинаковые внутренние сечения. Длину L считать заданной. Диаметр трубок мал по сравнению с длиной L.
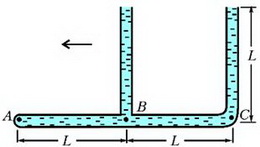
Рис. 3.
При движении тройника влево с ускорением а гидростатические давления в точках А, В и С (см. рис. 3) связаны между собой уравнением движения воды в горизонтальной трубке:
где ρ – плотность воды. Давление в точке С больше давления в точке В, поэтому вода будет выливаться из правой вертикальной трубки. Из условия неразрывности струи жидкость при этом будет отсасываться из левой вертикальной трубки. В установившемся режиме правая трубка будет полностью заполнена водой, а левая – частично. Поскольку вылилась 1/16 массы всей воды, что соответствует массе воды в части трубки длиной L/4, то в левой трубке останется столбик воды высотой 3/4L. Поэтому давления в точках В и С будут равны
где p0 – атмосферное давление.
Исключая из всех уравнений рB и рС, получим систему двух уравнений относительно рА и а:
Решая эту систему относительно рА, найдем
Задача 5. Тонкая, запаянная с одного конца и изогнутая под прямым углом трубка заполнена ртутью и закреплена на горизонтальной платформе, которая вращается с угловой скоростью ω вокруг вертикальной оси (рис. 4). При вращении платформы ртуть не выливается и полностью заполняет горизонтальное колено. Открытое колено трубки вертикально. Геометрические размеры установки указаны на рисунке; атмосферное давление р0; плотность ртути ρ. Найдите давление ртути у запаянного конца трубки.
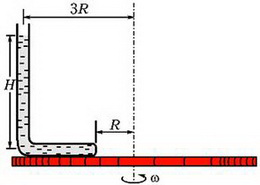
Рис. 4.
Выделим в горизонтальной части трубки небольшой элемент ртути длиной dr, расположенный на произвольном расстоянии r от оси вращения (рис. 5).
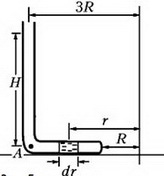
Рис. 5.
Этот элемент вращается в горизонтальной плоскости с угловой скоростью ω. Запишем уравнение движения выделенного элемента:
где S – площадь поперечного сечения трубки, dp – разность давлений между левым концом элемента ртути и правым. После сокращения на S получим связь между малыми приращениями dp и dr:
Проинтегрируем обе части этого уравнения и получим
Константу определим из условия, что при r = 3R (точка А) давление равно
и получим зависимость p(r)
Отсюда найдем давление ртути у запаянного конца трубки (r = R):
Задача 6. Стеклянный шар объемом V и плотностью ρ находится в сосуде с водой (рис. 6). Угол между стенкой сосуда и горизонтальным дном α, внутренняя поверхность сосуда гладкая, плотность воды ρ0. Найдите силу давления шара на дно сосуда в двух случаях: 1) сосуд неподвижен; 2) сосуд движется с постоянным горизонтальным ускорением а.
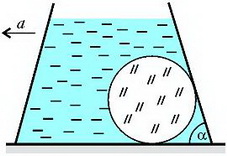
Рис. 6.
Сначала рассмотрим движущийся по горизонтали с постоянным ускорением а сосуд с водой. Введем систему координат XY, связанную с сосудом, как это изображено на рисунке 7.
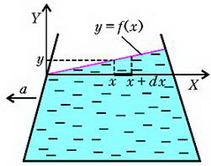
Рис. 7.
Наша задача – найти уравнение свободной поверхности жидкости в сосуде, который движется с горизонтальным ускорением а. Для этого выделим маленький элемент жидкости на оси Х, длина которого dx, а площадь поперечного сечения равна единице. С левого торца этого элемента давление равно
а с правого торца оно равно
где у – высота столба жидкости в точке х, а – аналогичная высота в точке . Так как наш элемент жидкости движется с ускорением а, его уравнение движения имеет вид
Отсюда получаем
или в интегральном виде —
Поскольку при х = 0 у = 0, константа тоже равна нулю, а уравнение свободной поверхности жидкости выглядит так:
Линии, параллельные свободной поверхности, внутри жидкости являются линиями постоянного давления. Таким образом, жидкость, движущаяся с горизонтальным ускорением а, эквивалентна неподвижной жидкости, находящейся в новом поле тяжести с эффективным «ускорением свободного падения», равным и направленным под углом к вертикали (рис. 8). Вертикальная составляющая этого эффективного ускорения равна обычному ускорению свободного падения g, а горизонтальная составляющая численно равна ускорению сосуда и направлена в противоположную сторону.
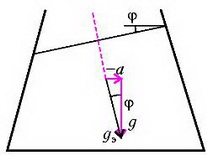
Рис. 8.
В том случае, когда сосуд неподвижен (а = 0), эффективное ускорение равно g и направлено по вертикали. Силы, действующие на стеклянный шар в этом случае, показаны на рисунке 9.
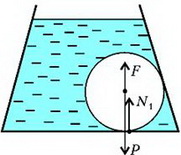
Рис. 9.
Здесь – вес (точнее – сила тяжести) шара, – выталкивающая сила, а N1 – сила реакции дна сосуда на шар. Из условия равновесия шара найдем, что
Очевидно, что сила давления шара на дно численно равна силе реакции дна и направлена в противоположную сторону.
В случае движущейся с горизонтальным ускорением a жидкости или неподвижной жидкости, но находящейся в поле с новым «ускорением свободного падения» gЭ, на шар будут действовать следующие силы (рис.10): вертикальная составляющая нового веса шара , горизонтальная составляющая этого веса , вертикальная составляющая выталкивающей силы , ее горизонтальная составляющая , реакция опоры Т со стороны боковой стенки и, наконец, сила N2 – сила реакции на шар со стороны дна сосуда. Запишем условие равновесия шара, т.е. равенство нулю всех сил, действующих на шар по вертикали:
и по горизонтали:
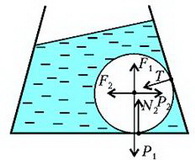
Рис. 10.
Исключая из этих уравнений Т, найдем искомую силу N2:
Разумеется, и в этом случае сила давления шара на дно сосуда численно равна силе реакции дна, но направлена в противоположную сторону.
Упражнения.
1. В цилиндрическом сосуде с водой плавает деревянная дощечка. Если на нее сверху положить стеклянную пластинку, то дощечка с пластинкой останутся на плаву, а уровень воды в сосуде повысится на Δh1. На сколько изменится уровень воды в сосуде с плавающей дощечкой, если ту же стеклянную пластинку бросить на дно сосуда? Плотность стекла ρст, плотность воды ρв.
2. U–образная трубка состоит из трех одинаковых колен, расположена вертикально и заполнена жидкостью (см. рис. 1). Один конец трубки соединен с баллоном, заполненным водородом, другой конец открыт в атмосферу. Водород в баллоне медленно нагревают, и он постепенно вытесняет жидкость из трубки. К моменту, когда из трубки вылилось 2/3 всей массы жидкости, водород получил количество теплоты Q = 30 Дж. Найдите объем баллона. Известно, что объем всей трубки равен объему баллона; атмосферное давление p0 = 105 Па; давление, создаваемое столбом жидкости в вертикальном колене трубки, равно p0/9.
3. «Тройник» из трех вертикальных открытых в атмосферу трубок полностью заполнен водой (рис. 11). После того, как тройник начали двигать в горизонтальном направлении в плоскости рисунка с некоторым ускорением, из него вылилось 9/32 всей массы воды. Чему равно ускорение тройника? Внутренние сечения трубок одинаковы, длина каждой трубки L.
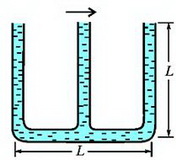
Рис. 11
4. Тонкая, запаянная с одного конца и изогнутая под прямым углом трубка заполнена жидкостью и закреплена на горизонтальной платформе, вращающейся с угловой скоростью ω вокруг вертикальной оси (рис. 12). Открытое колено трубки вертикально. Геометрические размеры установки указаны на рисунке; атмосферное давление p0; плотность жидкости ρ. Найдите давление жидкости у запаянного конца трубки.
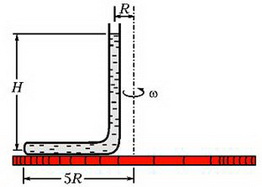
Рис. 12
Ответы.
1.
2.
3. .
4.
Источник
