В сосуде с водой плавает кусок льда с пузырьком воздуха

#хакнем_физика ???? рубрика, содержащая интересный, познавательный контент по физике как для школьников, так и для взрослых ????
Если решая математические задачи, следует руководствоваться только условиями, в том числе и неявно заданными (например: находя градусную меру одного из смежных углов в случаях, когда известна градусная мера другого, непременной частью условия является значение суммы градусных мер смежных углов, равной 180 град.), то при решении физических задач следует учитывать ВСЕ физические явления и процессы, влияющие на результат рассматриваемой в задаче ситуации.
Вот для примера известная и часто встречающаяся во многих учебниках и сборниках задач, в том числе и олимпиадных (и не только для семиклассников) по физике.
ЗАДАЧА
В стакане с водой плавает кусок льда. Изменится ли уровень воды, когда лёд растает?
Прежде чем продолжить чтение, предлагаю читателю дать (хотя бы для себя) обоснованный ответ на вопрос задачи…
В «Сборнике вопросов и задач по физике» [Н.И. Гольдфарб, изд. 2, «Высшая школа», М.: 1969] эта задача, помещённая как часть № 10.7 на стр. 48, на стр.193 приводится ответ:
«Лёд вытесняет воду, вес которой равен весу льда. Когда лёд растает, образуется такое же количество воды, поэтому уровень не изменится».
Такой же ответ приводится и во многих других сборниках…
А вот в популярнейшем и по сей день, выдержавшим множество изданий трёхтомнике «Элементарный учебник физики» под редакцией академика Г.С. Ландсберга [т. I, изд. 7, стереотипное, «Наука», М.: 1971] ответа на эту задачу (№ 162.2, стр. 351) не приводится. И это не случайно!
Что же не учтено в вышеприведённом ответе? Правильно! Не учтено, что при таянии льда вода в стакане охлаждается — именно поэтому мы и бросаем туда кусочек льда!
Вот как должен выглядеть правильный ответ:
«При таянии льда вода в стакане охлаждается. При охлаждении все вещества уменьшаются в объёме. Однако вода, единственная из всех известных веществ, имеет наибольшую плотность при температуре +4 град. С, а это значит, что при дальнейшем охлаждении данная масса воды увеличивается в объёме, что, как мне это было известно из курса природоведения в 5 классе (1961/1962 учебный год), является условием сохранения жизни на Земле, поскольку позволяет достаточно глубоким водоёмам не промерзать до самого дна!).
При этом возможно три варианта развития ситуации:
I. Если температура воды до начала таяния льда была выше 4 град. С и, хотя и понизилась после таяния льда, но осталась выше этой температуры, то уровень воды в стакане уменьшится.
II. Если температура воды до начала таяния льда была ниже 4 град. С, а после таяния льда ещё и уменьшилась, то уровень воды в стакане увеличится.
III. В случае, когда начальная температура воды была выше 4 град. С, а после того как лёд растаял, оказалась ниже этой температуры, то об уровне ничего определённого сказать нельзя — нужны конкретные данные о температуре и массе воды и льда, чтобы дать точный ответ на вопрос задачи!».
С этой задачей связана для меня одна интересная история.
Лет 15 назад во дворе дома, в котором я живу, ко мне с грустным выражением лица подошёл паренёк по имени Серёжа и попросил помочь подготовиться к предстоящей ему завтра апелляции по физике в нашем Политехническом институте (ныне Технический университет).
Поскольку времени было слишком мало, то я ограничился советом: если, по его мнению, апелляция пройдёт не очень удачно, и надежды исправить тройку на вступительном экзамене не будет, то попросить экзаменатора ответить на вопрос этой задачи и заставил его дословно вызубрить приведённый выше ответ и даже отработал с ним интонацию изложения этого ответа. На следующий вечер он подошёл ко мне с достаточно счастливым видом.
Вот его рассказ, каким я его запомнил:
«Всё получилось так, как Вы и хотели. Апелляцию проводили два человека: профессор и ассистент кафедры общей физики института. Мне выпало общаться с ассистентом, а профессор в это время общался с другим абитуриентом.
В ответ на мою просьбу ответить на мой вопрос ассистент слегка улыбнувшись сказал: «Пожалуйста…».
«После того, как я проговорил условие задачи, ассистент, широко улыбнувшись, произнёс: «Ну, это известная задача. Уровень воды не изменится — это следует из закона Архимеда: плавающий лёд вытесняет массу воды, равную массе льда. Образовавшаяся при таянии льда вода заполнит тот объём, который занимал в воде плавающий лёд…».
«Позвольте с Вами не согласиться», — начал я и затем совершенно спокойно слово в слово пересказал заготовленный нами ответ…
В это время профессор жестом остановил своего абитуриента и стал внимательно меня слушать…
Когда я закончил, возникла небольшая пауза…Профессор, обращаясь к ассистенту спросил: «Что скажешь?».
«Кажется, всё верно», — неуверенно ответил тот, на что профессор сказал, что никогда ещё не слышал столь аргументированного ответа, после чего, уже обращаясь ко мне, добавил: «Молодой человек, мы, к сожалению, не можем поднять Вам оценку сразу на два балла, но четвёрку Вы очевидно заслужили!»».
Мне остаётся лишь добавить, что Серёжа был зачислен студентом!…
Наши читатели могут поделиться своим мнением по поводу решения задачи. Если вам было интересно, не забудьте подписаться на наш канал и хэштег #хакнем_физика
Автор: #себихов_александр 71 год, много лет проработал конструктором-технологом микроэлектронных приборов и узлов в одном из НИИ г. Саратова, затем преподавателем математики и физики.
Другие статьи автора:
Вы читаете контент канала “Хакнем Школа”. Подпишитесь на наш канал, чтобы не терять его из виду.
Источник
Задачи, тесты
Е. М.
Раводин,
, МОУ СОШ № 2, г. Прокопьевск, Кемеровская обл.
Окончание. См. № 5,
8/2010
18. Прямоугольная коробочка из жести массой m = 76 г с дном площадью S = 38 см2 и высотой H = 6 см плавает в воде. Определите высоту h надводной части коробочки.
Решение. Коробочка плавает, если действующая на неё сила тяжести равна по модулю действующей на неё силе Архимеда: mg = FА, причём FА = Vпчgρв, где  – объём погружённой части коробочки. Подставляя числовые данные, получаем
– объём погружённой части коробочки. Подставляя числовые данные, получаем 
Отсюда глубина погружения коробочки равна

Значит h = H – x = 4 см.
19. Льдина плавает на поверхности пресной воды. Какую часть составляет объём подводной части от объёма всей льдины? Если задача не решается в общем виде, то, для упрощения, примите объём льдины равным 100 м3. Плотность льда 900 кг/м3.
Решение. Раз льдина плавает, то её сила тяжести равна по модулю силе Архимеда: mg = FА, т. е.:

20. На поверхности широкого озера лёд имеет толщину 2 м. Какой минимальной длины надо взять верёвку, чтобы зачерпнуть кружкой воды из проруби?
Решение. Так как озеро широкое, то лёд на его поверхности может только плавать, а не держаться за берега за счёт примерзания к ним. Согласно решению задачи № 19, в проруби под поверхностью воды окажется 0,9 толщи льда, т. е. 0,9 · 2 м = 1,8 м, а над поверхностью воды 0,2 м = 20 см. Для зачерпывания воды с такой глубины верёвка не нужна.
21. В стакане с пресной водой плавает кусок льда. Изменится ли уровень воды, когда лёд растает? Рассмотрите дополнительно случаи: когда в лёд вмёрзла дробинка; когда в лёд вмёрз пузырёк воздуха.
Решение. Лёд плавает, если его вес равен весу жидкости в объёме погружённой части. Образовавшаяся изо льда пресная вода имеет тот же вес, что и лёд, и, следовательно, точно заполнит объём, который вытеснял плавающий лёд. Значит, уровень воды не изменится.
Если во льду была дробинка, лёд вытеснял больше воды, чтобы поддерживать на плаву дробинку. Когда лёд растаял, дробинка утонула (её вес больше веса вытесненной ею воды), уровень воды понизился.
В случае вмёрзшего пузырька уровень воды после таяния льдины практически не изменится. Хотя, если подсчитать точно, уровень воды несколько понизится, т. к. масса воздуха в пузырьке хоть и мала, но не равна нулю.
22. В прямоугольный сосуд с водой пустили плавать модель судна массой m = 4 кг. На сколько при этом повысился уровень воды, если площадь дна сосуда S = 2000 см2?
Решение. Вес сосуда при опускании в него модели увеличится на вес модели mg. Это увеличение веса можно интерпретировать как следствие подъёма уровня воды на ∆h и, следовательно, увеличения силы давления воды ∆Fд = ρвg∆hS. Отсюда:

23. Кусок парафина массой m = 200 г плавает на границе раздела воды и бензина. Определите объём V1 надводной части бруска. Плотность парафина 900 кг/м3, бензина 700 кг/м3.
Решение. Если парафин плавает, то сила тяжести равна сумме сил Архимеда в обеих жидкостях: mg = Vвρвg + V1ρб g, где Vв – объём, погружённый в воду, V1 – искомый надводный объём (в бензине). Общий объём парафина 
Решая совместно оба уравнения, получаем:

24. Кусок льда, внутрь которого вморожен шарик из свинца, плавает в цилиндрическом сосуде с водой. Площадь дна сосуда S. Какова масса шарика, если после полного таяния льда уровень воды в сосуде понизился на H? Плотность свинца ρ1, плотность воды ρ2.
Решение. На плавающую льдину со свинцовым шариком действует бóльшая сила Архимеда, чем на такую же льдину без шарика, т. к. она тяжелее на силу тяжести шарика mg. Следовательно, объём вытесняемой в первом случае воды больше, чем во втором, на  Но когда льдина растает, шарик упадёт на дно и займёт объём V1 = m/ρ1. Общее уменьшение объёма воды в конечном счёте ∆V = ∆Vп – V1. Так как ∆V = SH (по условию), то приходим к уравнению:
Но когда льдина растает, шарик упадёт на дно и займёт объём V1 = m/ρ1. Общее уменьшение объёма воды в конечном счёте ∆V = ∆Vп – V1. Так как ∆V = SH (по условию), то приходим к уравнению: 
25. Корона царя Гиерона в воздухе весит P1 = 20 Н, а в воде P2 = 18,75 Н. Вычислите плотность вещества короны. Была ли она из чистого золота? Дополнение: найдите, сколько золота и сколько серебра было в короне. Плотность золота округлённо принять 20 000 кг/м3, а серебра 10 000 кг/м3.
Решение. Для оценки добросовестности мастера найдём плотность короны по формуле  полученной при решении задачи 9 (см. № 5/2010):
полученной при решении задачи 9 (см. № 5/2010):

– корона не из чистого золота.
Чтобы найти состав короны, используем два факта: 1) общая масса короны m = mз + mс; 2) общий объём короны V = Vз + Vс (индексы «з» и «с» относятся к золоту и серебру соответственно). Заменяя объёмы их выражениями через массы и плотности, получаем систему из двух уравнений:

Решение
Опуская громоздкие промежуточные вычисления, запишем ответ:

26. Какую силу надо приложить к пробковому телу массой 400 кг, чтобы удерживать его, когда оно целиком погружено в воду? ρп = 200 кг/м3; g = 10 м/с2.
Решение. Сила тяжести тела mg = 4000 Н направлена вниз, сила Архимеда направлена вверх и равна

Чтобы удержать тело в воде, надо приложить направленную вниз силу F = FА – mg = 16 кН.
27. Чугунная плита толщиной 0,5 м, длиной 10 м и шириной 4 м лежит на глинистом дне, выдавив из-под себя воду. Глубина водоёма 2,5 м. Какую силу необходимо приложить, чтобы начать подъём плиты?
Решение. Объём плиты V = 0,5 м · 10 м · 4 м = 20 м3.
Её масса m = Vρч = 20 м3 · 7000 кг/м3 = 140 000 кг.
Сила тяжести mg = 1 400 000 Н.
Поскольку под плитой нет воды, сила Архимеда на неё не действует. Вниз на плиту, кроме силы тяжести, действуют сила давления воды на глубине 2,5 – 0,5 = 2 (м) и сила давления атмосферы, которую передаёт вода по закону Паскаля. При нормальном атмосферном давлении общее давление на плиту:
p = pв + pа = 1,2 · 105 Па.
Горизонтальная площадь поверхности плиты
S = 40 м2. Сила давления на плиту F = pS = 4,8 · 106 Н.
Полная сила, прижимающая плиту к грунту:
F = mg + Fа = 1,4 · 106 Н + 4,8 · 106 Н = 6,2 ·106 Н.
Для отрыва от грунта нужна сила F > 6,2 МН.
Источник
| ( ««« »»» ) | ||
| Закон Архимеда без математических расчётов | ||
Математика представляет собой язык, на котором формулируются и решаются физические задачи. Тем не менее, для понимания элементарных (а может быть и фундаментальных) оснований науки об окружающем нас мире полезно познакомиться с задачами, решение которых не требует проведения математических расчётов. Вот несколько таких задач. 1. В небольшом бассейне плавает лодка. Изменится ли уровень воды в бассейне, если лежащий на дне лодки камень бросить в воду? Подумаем: зависит ли ответ на вопрос, поставленный в задаче, от формы дна лодки, на котором лежит камень? Ясно, что такой зависимости быть не может: в законе Архимеда форма тела, погруженного в жидкость, никакой роли не играет. Тогда будем мысленно «продавливать» камень через дно лодки. Последовательные стадии этого процесса представлены на рисунке. На одном из этапов камень можно представить подвешенным на верёвке, привязанной ко дну лодки. Уровень воды, естественно, не изменится, если удлинить верёвку так, чтобы камень коснулся дна бассейна. Если теперь веревку перерезать, очевидно, лодка всплывёт и, следовательно, уровень воды понизится. Аналогично решается и следующая задача. 2. В стакане с водой плавает кусок льда, содержащий: а) пузырёк воздуха; б) кусочек пробки; в) стальную гайку. Как изменится уровень воды в стакане, когда лёд растает? Заметим, что если лёд однороден, то после таяния уровень воды не изменится: лёд вытесняет ровно столько воды, сколько сам весит, а, следовательно, сколько получится при таянии. Также заметим, что решение поставленной задачи не зависит от места расположения указанных в условии задачи объектов в куске льда.
Пузырёк можно переместить к поверхности льда (см. рис.). То есть наличие пузырька равнозначно изменению формы льда, таяние которого, как мы уже заметили, уровень воды не изменяет. Гайку, как и в первой задаче, «продавим» сквозь лёд до дна стакана, а затем перережем связывающую ледяную нить. Лёд всплывёт, уровень воды понизится, и уже не изменится после таяния льда. Лёд с вмёрзшей пробкой после таяния не изменит уровень воды, так как пробку можно мысленно выдавить изо льда и пустить в самостоятельное плавание на тонкой ледяной нити. | ||
И в заключение – задача повышенной сложности. 3. Стакан наполовину заполнен водой, в которой плавает кусок льда. Поверх льда наливают керосин, верхний уровень которого устанавливается на высоте h от дна стакана. Как изменится эта высота, когда лёд растает? В случае, когда лёд оказывается под поверхностью керосина, ответ очевиден (вода, полученная после таяния льда, занимает меньший объём, значит верхний уровень керосина понизится). Интерес представляет анализ ситуации, когда лёд выступает над поверхностью льда (см. рисунок). Возникает соблазн деформировать лёд таким образом, чтобы его вершина оказалась под поверхностью керосина. Таким образом, казалось бы, можно было бы свести рассматриваемую задачу к предыдущей. Однако этот «фокус» не проходит: погружение выступающей части льда в керосин сопровождается повышением уровня жидкости. После таяния льда уровень понизится и конечный результат оказывается не очевидным.
Может, попробовать деформировать не лёд, а жидкость? Для этого слой керосина (толщиной h1) заменим таким слоем воды, который сохраняет положение льда. Поскольку плотность воды больше, чем плотность керосина, высота слоя h21. При таянии льда уровень воды (как было замечено выше) не меняется. Если теперь осуществить обратную замену и вернуть на место керосин (для этого следует оставить след поверхности льда, см. рисунок), то выяснится, что слой керосина над поверхностью, которую ранее образовывала вода, растекается по большей площади и уровень керосина понижается по сравнению с исходным, (см. рисунок). Итак, уровень керосина понижается независимо от того, покрывает керосин ледяную глыбу полностью или частично. Несмотря на то, что деформация льда не привела к решению, сама идея метода эквивалентных деформаций оказалась плодотворной! (C) 2010. Эпштейн Вячеслав Григорьевич (Украина, г.Харьков) | ||
Источник
А так ли хорошо знакома вам выталкивающая сила? // Квант. — 1990. — № 6. — С. 40-41.
По специальной договоренности с редколлегией и редакцией журнала “Квант”
Тела более легкие, чем жидкость, опущенные в эту жидкость
насильственно, будут выталкиваться вверх…
Тела более тяжелые, чем жидкость, опущенные в эту жидкость,
будут погружаться, пока не дойдут до самого низа…
Архимед, О плавающих телах
Герой этого выпуска «Калейдоскопа» — несомненно, Архимед. Древнегреческий ученый, с законом, которого вы знакомитесь едва ли не в самом начале изучения физики, заложил научные основы гидростатики. Они были развиты лишь в XVI—XVII столетиях Стевином, Галилеем, Паскалем, а окончательную формулировку получили уже в XIX веке. Кстати, именно труды Архимеда оказали решающее влияние на становление Галилея как ученого. О практическом же применении результатов архимедовых исследований и говорить не приходится, они хорошо вам известны – от кораблестроения до воздухоплавания.
Однако наглядность и простота многих задач на закон Архимеда – кажущаяся, порой они требуют серьезных размышлений. Попробуйте свои силы, не забывая, что надежны помощником вам будет эксперимент – а для проведения опытов наступившее лето дает столько возможностей.
Вопросы и задачи
- В сосуде с водой плавает в вертикальном положении брусок. Как изменится уровень воды в сосуде, если брусок перейдет в горизонтальное положенне?
- Однажды царь спросил у Архимеда, сколько нужно взять золота, чтобы его масса была равна массе слона. Как Архимед справился с задачей?
- На крюке динамометра висит ведерко. Изменится ли показание динамометра, если ведерко наполнить водой и погрузить в воду?
- Человек, несший автомобильную камеру, решил облегчить ношу. Для этого он накачал камеру, увеличив ее объем и рассчитывая использовать выталкивающую силу воздуха. Достиг ли он цели?
- Что тяжелее — тонна дерева или тонна железа?
- Изменится ли уровень воды в сосуде, если нить, удерживающую свинцовый шарик, удлинить так, чтобы шарик полностью погрузился в воду?
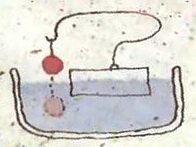
- Стальной шарик плавает в ртути. Изменится ли погружение шарика в ртуть, если сверху долить воды?
- Рыбак для хранения живой рыбы сделал в своей лодке ящик с отверстием в дне лодке. Не потонет ли она, если спустить ее на воду?
- В одном из сосудов с водой плавает кусок льда с пузырьком воздуха, в другом — с вмерзшим стальным шариком. Изменятся ли уровни воды в сосудах, когда лед растает?
- Одна из бутылок наполнена водой, другая — ртутью. Потонет ли первая бутылка, если ее опустить в воду? Потонет ли вторая, если ее опустить в ртуть?
- Что произойдет с уровнем воды в бассейне, если из лодки, плавающей в нем, бросить в него камень?
- Деревянный кубик лежит на дне сухого сосуда. Всплывет ли он, если в сосуд налить воду?
Микроопыт
Прикрепите к короткому отрезку стеариновой свечи небольшой грузик так, чтобы свеча, плавала в воде. Зажгите плавающую свечу и постарайтесь выяснить: погаснет ли пламя, как только сгорит отрезок, выступающий первоначально над водой?
Любопытно, что…
…история, связанная с короной царя Гиерона, добавила к прочим заслугам Архимеда почетное звание, по-видимому, первого известного нам ученого-детектива.
…в районах, впадения рек в море встречаются бревна, длительное время плавающие внутри воды на устойчивом расстояний от ее поверхности. Объясняется это меньшей, чем у морской, плотностью пресной воды. На разделе этих вод может оказаться древесина с промежуточной плотностью.
…на закон Архимеда многократно многократно опирались авторы проектов «вечных» двигателей. Подумайте, кстати, почему не мог действовать «двигатель», изображенный на рисунке.

…задачу под номером 11 как то предложили знаменитым физикам Дж. Гамову, Р. Оппенгеймеру и Ф. Блоху, и… все трое ответили неверно.
…до сих пор не обнаружен автор популярной школьной, частушки:
После сытного обеда
По закону Архимеда
Полагается поспать…
Хорошо бы узнать, какие физические соображения позволили автору связать выталкивающую силу с послеобеденным сном?
Что читать в «Кванте» о выталкивающей силе
- «Работа, энергии, и архимедова сила» — 1984, № 3, с. 27;
- «Закон Архимеда» — 1984, № 9, с. 30;
- «Повторим гидростатику» – 1985, № 2, с 48;
- «Закон Архимеда» — 1987, № 1, с. 29;
- «Архимедова сила в литературных произведениях» — 1988, № 5, с. 41;
- «Закон Архимеда с точки зрения математика» — 1989, № 10, с. 44.
Ответы
- Не изменится, так как количество вытесненной воды останется тем же.
- Погрузил сперва на плот слона, отметил уровень погружения; затем грузил слитки золота на плот до такого же погружения.
- Да, уменьшится на величину веса воды, вытесняемой стенками и дном ведра.
- Нет, поскольку, увеличив выталкивающую силу, человек более значительно увеличил вес своей ноши (плотность сжатого воздуха в камере больше плотности наружного воздуха).
- Вес в вакууме того дерева, которое в воздухе весит тонну, больше веса в вакууме того железа, которое весит в воздухе также одну тонну.
- Не изменится.
- Глубина погружения в ртуть уменьшится, так как возрастет выталкивающая сила за счет вытесненной шариком воды.
- Нет. Ящик и русло реки — сообщающиеся сосуды, и вода в ящике будет на таком же уровне, как и вода в реке.
- В первом — не изменится, во втором — понизится.
- Бутылка с водой потонет, с ртутью — нет.
- Когда камень находится в лодке, он вытесняет объем воды, масса которого равна массе камня. Поскольку плотность камня больше плотности воды, то объем вытесненной воды больше объема камня. Лежа на дне бассейна, камень вытесняет объем воды, равный лишь его собственному. Поэтому объем вытесненной им воды при попадании в бассейн уменьшается, и уровень падает.
- Да — если вода проникнет под кубик, нет — в противном случае.
Микроопыт
Сгорая, свеча уменьшается в весе и всплывает, поэтому горит дольше, чем кажется поначалу.
Источник
