В сосуде с водой плавает шайба

Решебник
ВСЕ
ФИЗИКА
МАТЕМАТИКА
ХИМИЯ
Задача по физике – 11566
В цилиндрическом сосуде с водой плавает брусок высотой $l$ и сечением $S$ (рис.). Какую работу необходимо совершить, чтобы с помощью тонкой стальной спицы брусок медленно опустить на дно стакана? Сечение стакана $S_{1} = 2S$, начальная высота воды в стакане $l$, плотность материала бруска $rho = 0,5 rho_{в}$, где $rho_{в}$ – плотность воды.
Подробнее
Задача по физике – 11567
Подвеска состоит из однородных стержней, соединенных шарнирно. Вес системы $P$. Определите натяжение нити AВ (рис.).
Подробнее
Задача по физике – 11568
Однородная цепочка длиной 2 м лежит на столе. Когда часть цепочки длиной 0,2 м опускают со стола, она начинает скользить вниз. Масса цепочки 5 кг, а сила трения между столом и цепочкой составляет 0,1 веса цепочки. Какая работа против силы трения совершается при соскальзывании цепочки?
Подробнее
Задача по физике – 11569
Автомобиль с двигателем мощностью $N_{1} = 30 кВт$ при перевозке груза развивает скорость $v_{1} = 15 м/с$. Автомобиль с двигателем мощностью $N_{2} = 20 кВт$ при тех же условиях развивает скорость $v_{2} = 10 м/с$. С какой скоростью будут двигаться автомобили, если их соединить тросом?
Подробнее
Задача по физике – 11570
Наблюдая за лодкой, ведущей на буксире другую такую же, можно заметить, что буксирный канат бывает натянут не все время. Объясните причину этого явления. (Мощность, развиваемая буксиром, постоянна.)
Подробнее
Задача по физике – 11571
В двух одинаковых сосудах ко дну прикреплены одинаковые тонкие нерастяжимые стальные стержни. На верхних концах стержней находятся одинаковые стальные шарики. Один из сосудов заполнен водой. Будет ли одинаковой потенциальная энергия шариков относительно дна этих сосудов?
Подробнее
Задача по физике – 11572
На полу лежат куб и шар, сделанные из стали. Масса их одинакова. Тела подняли до соприкосновения с потолком. Одинаково ли изменилась при этом их потенциальная энергия?
Подробнее
Задача по физике – 11573
Грузы, массой 100 г каждый, подвешены на одинаковых нитях длиной 25 и 75 см соответственно (рис.). Для какой из нитей более вероятен обрыв: короткой или длинной, если оба груза поднять на одинаковую высоту (до второго уровня) и отпустить?
Подробнее
Задача по физике – 11574
На какую глубину $l$ погрузится тело, упавшее с высоты $h$ в воду, если плотность вещества тела $rho$ меньше плотности воды $rho_{в}$? Трением о воздух и воду пренебречь.
Подробнее
Задача по физике – 11575
Земля движется вокруг Солнца со средней скоростью $v_{ср} = 29,8 км/с$. Зимой скорость движения больше, а летом меньше. Исчезает ли разность кинетических энергий Земли между зимним и летним периодом движения ее по орбите вокруг Солнца?
Подробнее
Задача по физике – 11576
Мячик массой $m$ и объемом $V$ мальчик погрузил на глубину $H$ в воду плотностью $rho$ и отпустил его. На какую высоту над поверхностью воды должен был выскочить мячик, если бы сопротивление воды (и воздуха) отсутствовало?
Подробнее
Задача по физике – 11577
В каком случае шина автомобиля при его движении больше нагреется: когда она слабо надута или надута хорошо?
Подробнее
Задача по физике – 11578
Одинаковые цилиндрические сообщающиеся сосуды с площадью сечения $S$ частично заполнены ртутью. На поверхности ртути лежат невесомые поршни. Когда на левый поршень положили груз весом $P$, уровни ртути в сосудах установились так, как показано на рисунке б. На сколько изменилась потенциальная энергия системы груз – ртуть?
Подробнее
Задача по физике – 11579
Стальной шарик массой $m = 50 г$ поднят на высоту $H =2 м$ над стальной плитой и отпущен, после чего он многократно отскакивает от плиты. Через некоторое время высота его подъема стала равной $H_{1} = 1,5 м$. Какое количество теплоты выделилось за это время в результате столкновения шарика с плитой и трения о воздух?
Подробнее
Задача по физике – 11580
Ко дну правой части сосуда приморожен брусок льда. Сосуд частично заполнен водой и установлен на ребро неподвижной призмы (рис.). Нарушится ли равновесие сосуда, если лед растает?
Подробнее
Источник
Решебник
ВСЕ
ФИЗИКА
МАТЕМАТИКА
ХИМИЯ
Задача по физике – 75
В большом сосуде с водой плавает в вертикальном положении тонкостенный стакан, в который налито некоторое количество воды. Разность уровней воды в сосуде и стакане равна х. Как изменится эта разность, если в стакан опустить пробку?
Подробнее
Задача по физике – 76
Толстостенная лодка с вертикальными стенками и отверстием в дне достаточно долго свободно плавает в озере. Затем отверстие снаружи затыкают и внутрь лодки опускают бревно. Повысится или понизится после этого уровень воды в лодке относительно уровня воды в озере? Почему?
Подробнее
Задача по физике – 77
Шайба массой М, имеющая форму цилиндра с площадью основания S и высотой h, плавает на границе раздела двух несмешивающихся жидкостей с плотностями $rho_{1}$ и $rho_{2}$ ($rho_{1}
Подробнее
Задача по физике – 78
Кубик плавает в сосуде с водой так, что его верхняя грань параллельна поверхности воды. При этом половина кубика погружена в воду. Какой слой масла надо долить, чтобы кубик плавал полностью погруженным в жидкость, если плотность масла в два раза меньше плотности воды и длина ребра кубика равна а? Масло с водой не смешивается.
Подробнее
Задача по физике – 79
Вес Р системы, состоящей из стакана с водой и пробкового шарика, измеряется в пяти случаях:
1) шарик свободно плавает в стакане (показание весов $P_{1}$);
2) шарик лежит на чаше весов рядом со стаканом ($P_{2}$);
3) шарик удерживается в полностью погруженном состоянии тонкой невесомой нитью, прикрепленной ко дну стакана ($P_{з}$);
4) шарик удерживается в полностью погруженном состоянии тонкой невесомой спицей, закрепленной над стаканом ($P_{4}$);
5) * шарик, удерживавшийся в утопленном состоянии, освобождается и начинает свободно всплывать ($P_{5}$).
Расставьте показания весов в порядке их возрастания.
Подробнее
Задача по физике – 80
На чашке весов стоят гиря и стакан с водой. Сравните показание весов Р с показаниями весов в следующих случаях:
1) гиря подвешена на нити к внешнему штативу и погружена в воду ($P_{1}$);
2) * подвес оборвался, и гиря начинает тонуть ($P_{2}$).
Подробнее
Задача по физике – 81
Пробка прикреплена посредством легкой пружинки к дну сосуда с водой. И пробка и пружинка полностью погружены в воду. Увеличится или уменьшится длина пружинки, если сосуд начнет двигаться вертикально вверх (вниз) с постоянным ускорением?
Подробнее
Задача по физике – 82
В сосуд с водой опущена труба диаметром d.В трубу поместили шарик того же диаметра. Центр шарика оказался на глубине h. Найдите плотность вещества шарика. Зазор между трубой и шариком отсутствует. Сила трения между ними равна нулю.
Подробнее
Задача по физике – 83
Раковина в ванной комнате имеет сливное отверстие радиусом r. В раковину опускают шар массой m и радиусом R > r и начинают медленно наливать воду. Опишите качественно дальнейшее поведение системы в зависимости от соотношения между m, R, r.
Подробнее
Задача по физике – 84
Шарик, плотность которого меньше плотности волы, с помощью тонкой нити прикреплен к дну большого сосуда, заполненного водой. Сосуд движется вправо с ускорением а. В какую сторону и на какой угол $alpha$; отклонена нить от вертикали?

Подробнее
Задача по физике – 85
На горизонтальной плоскости лежит капля ртути объемом V. Сверху на каплю поставили брусок массой М так, что капля сильно сплющилась (рис.). Оцените расстояние h между бруском и плоскостью, если коэффициент поверхностного натяжения ртути $omega$ и все поверхности абсолютно не смачиваются ртутью.
Подробнее
Задача по физике – 86
Металлическая иголка диаметром d = 1 мм и длиной $l ll d$ смазана жиром так, что ее поверхность абсолютно не смачивается водой. Найдите максимально возможную плотность $rho$ вещества иголки. при которой она не будет тонуть в воде. Коэффициент поверхностного натяжения воды а принять равным 0,07 Н/м, а ускорение свободного падения $g = 10 м/с^{2}$ .
Подробнее
Задача по физике – 87
Шарик массой m, подвешенный на невесомой нерастяжимой нити вращается по окружности вокруг вертикальной оси с постоянной угловой скоростью $omega$ (эта система носит название “конический маятник, рис. а). Где нить конического маятника должна быть прочнее – на Земле или на Луне?

Подробнее
Задача по физике – 88
Два одинаковых массивных шарика скреплены невесомой пружиной. Шарики летят с одинаковой скоростью v, как показано на рис. а. Сила тяжести отсутствует. Как будут двигаться шарики после столкновения со стенкой, если удар о стенку абсолютно упругий и время удара шарика о стенку много меньше периода собственных колебаний системы?

Подробнее
Задача по физике – 89
Малое тело массой $m = 10 г$ подвешено на нити AB к пружине с жесткостью $k = 10 кг/с^{2}$ (рис.). Пружина и нить невесомы, нить нерастяжима. Система совершает гармонические колебания в вертикальном направлении в поле тяжести. Может ли амплитуда А этих колебаний быть равна 1 см?
Подробнее
Источник
Задачи, тесты
Е. М.
Раводин,
, МОУ СОШ № 2, г. Прокопьевск, Кемеровская обл.
Окончание. См. № 5,
8/2010
18. Прямоугольная коробочка из жести массой m = 76 г с дном площадью S = 38 см2 и высотой H = 6 см плавает в воде. Определите высоту h надводной части коробочки.
Решение. Коробочка плавает, если действующая на неё сила тяжести равна по модулю действующей на неё силе Архимеда: mg = FА, причём FА = Vпчgρв, где – объём погружённой части коробочки. Подставляя числовые данные, получаем
Отсюда глубина погружения коробочки равна
Значит h = H – x = 4 см.
19. Льдина плавает на поверхности пресной воды. Какую часть составляет объём подводной части от объёма всей льдины? Если задача не решается в общем виде, то, для упрощения, примите объём льдины равным 100 м3. Плотность льда 900 кг/м3.
Решение. Раз льдина плавает, то её сила тяжести равна по модулю силе Архимеда: mg = FА, т. е.:
20. На поверхности широкого озера лёд имеет толщину 2 м. Какой минимальной длины надо взять верёвку, чтобы зачерпнуть кружкой воды из проруби?
Решение. Так как озеро широкое, то лёд на его поверхности может только плавать, а не держаться за берега за счёт примерзания к ним. Согласно решению задачи № 19, в проруби под поверхностью воды окажется 0,9 толщи льда, т. е. 0,9 · 2 м = 1,8 м, а над поверхностью воды 0,2 м = 20 см. Для зачерпывания воды с такой глубины верёвка не нужна.
21. В стакане с пресной водой плавает кусок льда. Изменится ли уровень воды, когда лёд растает? Рассмотрите дополнительно случаи: когда в лёд вмёрзла дробинка; когда в лёд вмёрз пузырёк воздуха.
Решение. Лёд плавает, если его вес равен весу жидкости в объёме погружённой части. Образовавшаяся изо льда пресная вода имеет тот же вес, что и лёд, и, следовательно, точно заполнит объём, который вытеснял плавающий лёд. Значит, уровень воды не изменится.
Если во льду была дробинка, лёд вытеснял больше воды, чтобы поддерживать на плаву дробинку. Когда лёд растаял, дробинка утонула (её вес больше веса вытесненной ею воды), уровень воды понизился.
В случае вмёрзшего пузырька уровень воды после таяния льдины практически не изменится. Хотя, если подсчитать точно, уровень воды несколько понизится, т. к. масса воздуха в пузырьке хоть и мала, но не равна нулю.
22. В прямоугольный сосуд с водой пустили плавать модель судна массой m = 4 кг. На сколько при этом повысился уровень воды, если площадь дна сосуда S = 2000 см2?
Решение. Вес сосуда при опускании в него модели увеличится на вес модели mg. Это увеличение веса можно интерпретировать как следствие подъёма уровня воды на ∆h и, следовательно, увеличения силы давления воды ∆Fд = ρвg∆hS. Отсюда:
23. Кусок парафина массой m = 200 г плавает на границе раздела воды и бензина. Определите объём V1 надводной части бруска. Плотность парафина 900 кг/м3, бензина 700 кг/м3.
Решение. Если парафин плавает, то сила тяжести равна сумме сил Архимеда в обеих жидкостях: mg = Vвρвg + V1ρб g, где Vв – объём, погружённый в воду, V1 – искомый надводный объём (в бензине). Общий объём парафина
Решая совместно оба уравнения, получаем:
24. Кусок льда, внутрь которого вморожен шарик из свинца, плавает в цилиндрическом сосуде с водой. Площадь дна сосуда S. Какова масса шарика, если после полного таяния льда уровень воды в сосуде понизился на H? Плотность свинца ρ1, плотность воды ρ2.
Решение. На плавающую льдину со свинцовым шариком действует бóльшая сила Архимеда, чем на такую же льдину без шарика, т. к. она тяжелее на силу тяжести шарика mg. Следовательно, объём вытесняемой в первом случае воды больше, чем во втором, на Но когда льдина растает, шарик упадёт на дно и займёт объём V1 = m/ρ1. Общее уменьшение объёма воды в конечном счёте ∆V = ∆Vп – V1. Так как ∆V = SH (по условию), то приходим к уравнению:
25. Корона царя Гиерона в воздухе весит P1 = 20 Н, а в воде P2 = 18,75 Н. Вычислите плотность вещества короны. Была ли она из чистого золота? Дополнение: найдите, сколько золота и сколько серебра было в короне. Плотность золота округлённо принять 20 000 кг/м3, а серебра 10 000 кг/м3.
Решение. Для оценки добросовестности мастера найдём плотность короны по формуле полученной при решении задачи 9 (см. № 5/2010):
– корона не из чистого золота.
Чтобы найти состав короны, используем два факта: 1) общая масса короны m = mз + mс; 2) общий объём короны V = Vз + Vс (индексы «з» и «с» относятся к золоту и серебру соответственно). Заменяя объёмы их выражениями через массы и плотности, получаем систему из двух уравнений:
Решение
Опуская громоздкие промежуточные вычисления, запишем ответ:
26. Какую силу надо приложить к пробковому телу массой 400 кг, чтобы удерживать его, когда оно целиком погружено в воду? ρп = 200 кг/м3; g = 10 м/с2.
Решение. Сила тяжести тела mg = 4000 Н направлена вниз, сила Архимеда направлена вверх и равна
Чтобы удержать тело в воде, надо приложить направленную вниз силу F = FА – mg = 16 кН.
27. Чугунная плита толщиной 0,5 м, длиной 10 м и шириной 4 м лежит на глинистом дне, выдавив из-под себя воду. Глубина водоёма 2,5 м. Какую силу необходимо приложить, чтобы начать подъём плиты?
Решение. Объём плиты V = 0,5 м · 10 м · 4 м = 20 м3.
Её масса m = Vρч = 20 м3 · 7000 кг/м3 = 140 000 кг.
Сила тяжести mg = 1 400 000 Н.
Поскольку под плитой нет воды, сила Архимеда на неё не действует. Вниз на плиту, кроме силы тяжести, действуют сила давления воды на глубине 2,5 – 0,5 = 2 (м) и сила давления атмосферы, которую передаёт вода по закону Паскаля. При нормальном атмосферном давлении общее давление на плиту:
p = pв + pа = 1,2 · 105 Па.
Горизонтальная площадь поверхности плиты
S = 40 м2. Сила давления на плиту F = pS = 4,8 · 106 Н.
Полная сила, прижимающая плиту к грунту:
F = mg + Fа = 1,4 · 106 Н + 4,8 · 106 Н = 6,2 ·106 Н.
Для отрыва от грунта нужна сила F > 6,2 МН.
Источник
6. Механика (изменение физических величин в процессах)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Деревянный шарик плавает в воде. Как изменятся сила Архимеда и высота части шара, выступающей над поверхностью жидкости, если шар перенести в сосуд с маслом?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Сила Архимеда}&text{Высота части шара, выступающей над поверхностью воды}\
hline
&\
hline
end{array}]
1) Так как шар плавает в жидкости, то сила Архимеда уравновешивает силу тяжести, а так как сила тяжести не изменилась, значит, сила Архимеда не изменилась. Ответ — 3
2) Сила Архимеда находится по формуле: (F_text{арх}=rho g V_text{т}), где (rho) — плотность жидкости, (V_text{т}) — объем тела погруженного в жидкость. Так как (F_text{арх}) не изменилась, (rho) уменьшилась, а (g) постояна, то (V_text{т}) увеличится, следовательно, высота части шара, выступающей над жидкостью уменьшится. Ответ — 2
Ответ: 32
Деревянный шарик плавает в воде. Как изменятся давление на дно сосуда и сила тяжести, если шар перенести в сосуд с маслом? (Сосуды одинаковые, уровень жидкости до погружения шарика одинаковый.)
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Сила тяжести}&text{Сила давления на дно}\
hline
&\
hline
end{array}]
1) Сила тяжести находится по формуле: (F=mg), так как масса шарика не меняется, то и сила тяжести не изменяется. Ответ — 3
2) Сила давления находится по формуле: ( displaystyle F=rho g h S), где (rho) — плотность жидкости, (h) — высота столба жидкости (S) — площадь дна, или эту формулу можно заменить на равносильную [F=m_1g] (m_1) – масса жидкости, так как плотность воды больше плотности масла, то масса жидкости уменьшилась, значит, сила давления уменьшилась. Ответ — 2
Ответ: 32
На поверхности воды плавает небольшая льдинка. Как изменятся сила Архимеда, действующая на льдинку, и давление на дно сосуда, если часть льдинки растает?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Сила Архимеда}&text{Давление на дно сосуда}\
hline
&\
hline
end{array}]
1) Так как часть льда растает, то (m_text{л}) уменьшится. Так как лед плавает, то сила архимеда уравновешивает силу тяжести. [F_text{а}=m_text{л}g] А так как масса льда уменьшилась, то и сила Архимеда уменьшилась. Ответ — 2
2) Так как лед плавает, то [F_text{а}=m_text{л}g] или (m_text{л}=rho_text{в}V_text{т}), где (rho_text{в}) — плотность воды, а (V_text{т}) — объем погруженной части тела.
Выразим объем погруженной части [V_text{т}=frac{m_text{л}}{rho_text{в}} quad (1)] Объем полученной воды равен [V_text{в}=frac{m_text{л}}{rho_text{в}} quad (2)] Из (1) и (2) можно сделать вывод, что ( V_ text{в}=V_text{т}), а значит объем погруженной в воду части льда будет замещен после таяния льда таким же объемом воды, что означает: уровень воды в сосуде не изменится. Ответ — 3
Ответ: 23
На поверхности воды плавает деревянный брусок плотностью (rho_1)=700 кг/м(^3). Как изменятся следующие величины: уровень воды и сила Архимеда, действующая на брусок, если заменить деревянный брусок, на брусок такого же объема, но плотностью (rho_2 )=1400 кг/м(^3)?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Уровень воды}&text{Сила Архимеда}\
hline
&\
hline
end{array}]
1) Объем погруженной части равен объему вытесненной жидкости, а так как (rho_2>rho_1), то тело погрузится глубже, а значит и уровень воды увеличится. Ответ — 1
2) Сила архимеда находится по формуле: [F_text{a}=rho_text{в}g V_text{п}] Где (rho_text{в}) — плотность воды, а (V_text{п}) — объем тела погруженного в воду. Так как (rho_2 >rho_text{в}), то тело тонет в жидкости и объем погруженной части увеличивается, а следовательно и увеличивается сила Архимеда. Ответ — 1
Ответ: 11
В сосуде, наполненным водой, проводят 3 опыта. Опыт 1: кладут брусок плотностью (rho_2)=1400 кг/м(^3). Опыт 2: кладут брусок плотностью (rho_3)=2100 кг/м(^3). Опыт 3: вначале брусок плотностью (rho_2)=1400 кг/м(^3), а затем брусок того же объема, но плотностью (rho_3)=2100 кг/м(^3). Как изменится сила Архимеда в опыте 2 относительно опыта 1 и уровень воды в опыте 3?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Сила Архимеда в опыте 2 относительно опыта 1}&text{Уровень воды в опыте 3}\
hline
&\
hline
end{array}]
1) Так как (rho_2) и (rho_3) больше (rho_text{в}), где (rho_text{в}) — плотность воды, то бруски в опытах 1 и 2 тонут , а значит погружаются на полный объем. Сила архимеда находится по формуле [F_text{a}=rho_text{в}g V_text{п}] Где (rho_text{в}) — плотность воды, а (V_text{п}) — объем тела погруженного в воду. Так как плотность жидкости одинаковая и объем погруженного тела одинаковый, то и сила Архимеда одинаковая. Ответ — 3
2) Как выяснили в 1) бруски плотностью (rho_2) и (rho_3) тонут в воде, а значит и вытесняют одинаковый объем жидкости, следовательно и уровень жидкости не изменяется. Ответ — 3
Ответ: 33
К деревянному бруску, плавающему в воде, привязали на тонкой нити небольшой стальной шарик, после привязывания система находится в равновесии. Как изменятся следующие величины: сила архимеда, действующая на брусок, и уровень воды? Считать, что брусок не утонул.
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Сила Архимеда, действующая на брусок}&text{Уровень воды}\
hline
&\
hline
end{array}]
Обозначим все силы, действуюющие только на брусок: 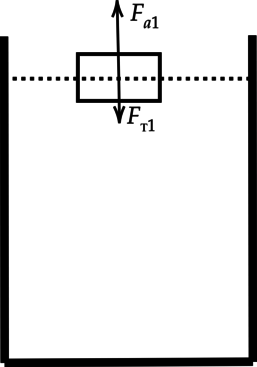
Обозначим все силы, действующие на систему брусок+шарик: 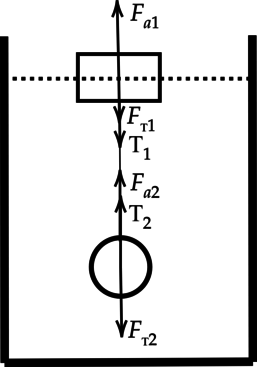
1) Как мы видим на первом рисунке ( F_ text{a1}=F_text{т1} ). На втором рисунке распишем все силы: [F_text{a1}+F_text{a2}+ T_2=F_text{т1}+F_text{т2}+T_1] Так как (T_1=T_2), то можно заменить [F_text{a1}+F_text{a2}=F_text{т1}+F_text{т2}] Кроме того, шарик, сделанный из стали, тонет в воде, а значит (F_text{т2}>F_text{a2}). Значит, и (F_text{a1}) должна увеличится, для того, чтобы равенство соблюдалось. Ответ — 1
2) Сила Архимеда находится по формуле: [F_text{а}=rho g V] где (rho) — плотность жидкости, (V) — объем погруженной части тела в жидкость. Так как сила Архимеда увеличилась, а плотность осталась неизменной, то (V) увеличился, значит и количество вытесненной воды увеличится и уровень воды поднимется. Ответ — 1
Ответ: 11
На поверхности воды плавает деревянный брусок. Как изменятся сила Архимеда, действующая на брусок, и масса вытесненной воды, если брусок заменить на другой с той же массой (m), но меньшей плотностью (rho)?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Сила Архимеда}&text{Масса вытесненной воды}\
hline
&\
hline
end{array}]
1) Так как брусок плавает на поверхности, то сила Архимеда уравновешивает силу тяжести. [F_a=mg] Так как масса не изменилась, то и сила Архимеда не изменилась. Ответ — 3
2) Сила Архимеда находится по формуле: [F_a=rho_1gV] Где (rho_1) — плотность жидкости, а (V) — объем погруженной части тела в жидкость. В пункте 1) доказали, что сила Архимеда не изменилась, а так как (rho_1) осталась неизменной, то и (V) тоже не изменился. Значит и масса вытесненной воды не изменилась. Ответ — 3
Ответ: 33
Источник
