В сосуде с водой плавает шар

6. Механика (изменение физических величин в процессах)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Деревянный шарик плавает в воде. Как изменятся сила Архимеда и высота части шара, выступающей над поверхностью жидкости, если шар перенести в сосуд с маслом?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Сила Архимеда}&text{Высота части шара, выступающей над поверхностью воды}\
hline
&\
hline
end{array}]
1) Так как шар плавает в жидкости, то сила Архимеда уравновешивает силу тяжести, а так как сила тяжести не изменилась, значит, сила Архимеда не изменилась. Ответ — 3
2) Сила Архимеда находится по формуле: (F_text{арх}=rho g V_text{т}), где (rho) — плотность жидкости, (V_text{т}) — объем тела погруженного в жидкость. Так как (F_text{арх}) не изменилась, (rho) уменьшилась, а (g) постояна, то (V_text{т}) увеличится, следовательно, высота части шара, выступающей над жидкостью уменьшится. Ответ — 2
Ответ: 32
Деревянный шарик плавает в воде. Как изменятся давление на дно сосуда и сила тяжести, если шар перенести в сосуд с маслом? (Сосуды одинаковые, уровень жидкости до погружения шарика одинаковый.)
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Сила тяжести}&text{Сила давления на дно}\
hline
&\
hline
end{array}]
1) Сила тяжести находится по формуле: (F=mg), так как масса шарика не меняется, то и сила тяжести не изменяется. Ответ — 3
2) Сила давления находится по формуле: ( displaystyle F=rho g h S), где (rho) — плотность жидкости, (h) — высота столба жидкости (S) — площадь дна, или эту формулу можно заменить на равносильную [F=m_1g] (m_1) – масса жидкости, так как плотность воды больше плотности масла, то масса жидкости уменьшилась, значит, сила давления уменьшилась. Ответ — 2
Ответ: 32
На поверхности воды плавает небольшая льдинка. Как изменятся сила Архимеда, действующая на льдинку, и давление на дно сосуда, если часть льдинки растает?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Сила Архимеда}&text{Давление на дно сосуда}\
hline
&\
hline
end{array}]
1) Так как часть льда растает, то (m_text{л}) уменьшится. Так как лед плавает, то сила архимеда уравновешивает силу тяжести. [F_text{а}=m_text{л}g] А так как масса льда уменьшилась, то и сила Архимеда уменьшилась. Ответ — 2
2) Так как лед плавает, то [F_text{а}=m_text{л}g] или (m_text{л}=rho_text{в}V_text{т}), где (rho_text{в}) — плотность воды, а (V_text{т}) — объем погруженной части тела.
Выразим объем погруженной части [V_text{т}=frac{m_text{л}}{rho_text{в}} quad (1)] Объем полученной воды равен [V_text{в}=frac{m_text{л}}{rho_text{в}} quad (2)] Из (1) и (2) можно сделать вывод, что ( V_ text{в}=V_text{т}), а значит объем погруженной в воду части льда будет замещен после таяния льда таким же объемом воды, что означает: уровень воды в сосуде не изменится. Ответ — 3
Ответ: 23
На поверхности воды плавает деревянный брусок плотностью (rho_1)=700 кг/м(^3). Как изменятся следующие величины: уровень воды и сила Архимеда, действующая на брусок, если заменить деревянный брусок, на брусок такого же объема, но плотностью (rho_2 )=1400 кг/м(^3)?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Уровень воды}&text{Сила Архимеда}\
hline
&\
hline
end{array}]
1) Объем погруженной части равен объему вытесненной жидкости, а так как (rho_2>rho_1), то тело погрузится глубже, а значит и уровень воды увеличится. Ответ — 1
2) Сила архимеда находится по формуле: [F_text{a}=rho_text{в}g V_text{п}] Где (rho_text{в}) — плотность воды, а (V_text{п}) — объем тела погруженного в воду. Так как (rho_2 >rho_text{в}), то тело тонет в жидкости и объем погруженной части увеличивается, а следовательно и увеличивается сила Архимеда. Ответ — 1
Ответ: 11
В сосуде, наполненным водой, проводят 3 опыта. Опыт 1: кладут брусок плотностью (rho_2)=1400 кг/м(^3). Опыт 2: кладут брусок плотностью (rho_3)=2100 кг/м(^3). Опыт 3: вначале брусок плотностью (rho_2)=1400 кг/м(^3), а затем брусок того же объема, но плотностью (rho_3)=2100 кг/м(^3). Как изменится сила Архимеда в опыте 2 относительно опыта 1 и уровень воды в опыте 3?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Сила Архимеда в опыте 2 относительно опыта 1}&text{Уровень воды в опыте 3}\
hline
&\
hline
end{array}]
1) Так как (rho_2) и (rho_3) больше (rho_text{в}), где (rho_text{в}) — плотность воды, то бруски в опытах 1 и 2 тонут , а значит погружаются на полный объем. Сила архимеда находится по формуле [F_text{a}=rho_text{в}g V_text{п}] Где (rho_text{в}) — плотность воды, а (V_text{п}) — объем тела погруженного в воду. Так как плотность жидкости одинаковая и объем погруженного тела одинаковый, то и сила Архимеда одинаковая. Ответ — 3
2) Как выяснили в 1) бруски плотностью (rho_2) и (rho_3) тонут в воде, а значит и вытесняют одинаковый объем жидкости, следовательно и уровень жидкости не изменяется. Ответ — 3
Ответ: 33
К деревянному бруску, плавающему в воде, привязали на тонкой нити небольшой стальной шарик, после привязывания система находится в равновесии. Как изменятся следующие величины: сила архимеда, действующая на брусок, и уровень воды? Считать, что брусок не утонул.
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Сила Архимеда, действующая на брусок}&text{Уровень воды}\
hline
&\
hline
end{array}]
Обозначим все силы, действуюющие только на брусок: 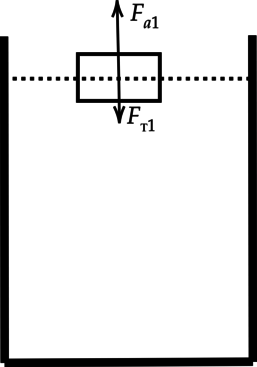
Обозначим все силы, действующие на систему брусок+шарик: 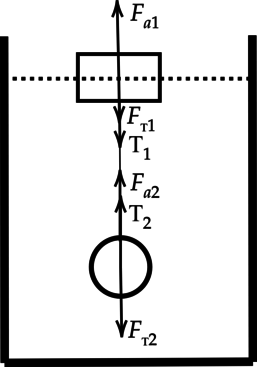
1) Как мы видим на первом рисунке ( F_ text{a1}=F_text{т1} ). На втором рисунке распишем все силы: [F_text{a1}+F_text{a2}+ T_2=F_text{т1}+F_text{т2}+T_1] Так как (T_1=T_2), то можно заменить [F_text{a1}+F_text{a2}=F_text{т1}+F_text{т2}] Кроме того, шарик, сделанный из стали, тонет в воде, а значит (F_text{т2}>F_text{a2}). Значит, и (F_text{a1}) должна увеличится, для того, чтобы равенство соблюдалось. Ответ — 1
2) Сила Архимеда находится по формуле: [F_text{а}=rho g V] где (rho) — плотность жидкости, (V) — объем погруженной части тела в жидкость. Так как сила Архимеда увеличилась, а плотность осталась неизменной, то (V) увеличился, значит и количество вытесненной воды увеличится и уровень воды поднимется. Ответ — 1
Ответ: 11
На поверхности воды плавает деревянный брусок. Как изменятся сила Архимеда, действующая на брусок, и масса вытесненной воды, если брусок заменить на другой с той же массой (m), но меньшей плотностью (rho)?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
[begin{array}{|c|c|}
hline
text{Сила Архимеда}&text{Масса вытесненной воды}\
hline
&\
hline
end{array}]
1) Так как брусок плавает на поверхности, то сила Архимеда уравновешивает силу тяжести. [F_a=mg] Так как масса не изменилась, то и сила Архимеда не изменилась. Ответ — 3
2) Сила Архимеда находится по формуле: [F_a=rho_1gV] Где (rho_1) — плотность жидкости, а (V) — объем погруженной части тела в жидкость. В пункте 1) доказали, что сила Архимеда не изменилась, а так как (rho_1) осталась неизменной, то и (V) тоже не изменился. Значит и масса вытесненной воды не изменилась. Ответ — 3
Ответ: 33
Источник
В интернете периодически выкладывают одни и те же задачки, которые вроде бы уже и разобраны досконально, по ним уже даже сняты видеоопыты, но все равно есть значительная часть людей, которые уверены, что ответ тут будет совсем другой.
Вот например задачка на картинке. Сколько ее не выкладывай, ответы будут постоянно разные.
Ну, ответте и вы тогда уж:
В какую сторону отклонятся весы?
Правая чаша опустится вниз
Левая чаша опустится вниз
Система останется в равновесии
Вот самые популярные объяснения из интернета:
1. Весы наклонятся налево потому что:
– слева вес равен давлению столба жидкости на дно ёмкости + вес шарика , а справа вес равен только давлению столба жидкости .
соответственно при заданных условиях вес слева будет больше веса справа .
– Налево по идее. Потому что стальной шарик подвешен, дна не касается. Значит справа давит только вода. А слева маленькое преимущество дает шарик
– Левый стакан тяжелее, там в системе, кроме воды и стакана – еще и шарик. Для него можно рассматривать вариант без нити, с шариком плавающим на поверхности.
– Зачем рассматривать то что творится в колбах. Достаточно знать, что колбы одинаковые, в них налито равное количество воды, но в одной колбе находится еще и шарик для пинг-понга, в то время как во второй ничего. Если бы опора металлического шарика находилась на чаше весов то перевес бы был со стороны металлического шарика. В данном случае перевесит колба с легким шариком.
– Металлический шарик никак не влияет на массу стакана. Значит, масса левой чашки весов будет больше на массу шарика для пинг понга
2. Весы наклонятся направо, потому что:
– Вода толкает шарик вверх, сама отталкиваясь от него вниз. Слева действие выталкивающей силы компенсируется силой натяжения нити.
– представим пустую ванну (для простоты будем считать, что она пластиковая и ничего не весит). В ванну лег человек весом 100 кг. Сколько будет весить ванна? 100 кг.
Теперь нальем туда 100 литров воды. Сколько будет весить ванна? 200 килограмм. Теперь подвесим человека на тросе, так что-бы он остался в воде. Весь-ли вес человека придется на трос? Нет, на трос придется часть веса, потому-что в воде он стал легче. Предположим, что объем человека – 50 литров, соответственно в воде он весит на 50 кг меньше.
Соответственно, на тросе повиснет 50 кг. Значит в ванне останется на 50 кг меньше. Значит ванна будет весить 150 кг. А левая чашка… нет разницы плавает там шарик или брошен на воду – там изменится только форма воды, а вес увеличиться на вес этого пластикового шарика.
– Правая чашка весов: После погружения стального шарика в воду, его вес (сила действующая на нить, на которой он висит) уменьшилась на вес вытесненной им воды. Компенсировать это изменение веса можно только за счёт увеличение веса стакана с водой.
Левая чашка весов: Подъём уровня воды из-за погружённого в воду шарика (весом которого можно пренебречь) равносилен тому, что вода находится просто в более узком сосуде. Никакого изменения веса стакана не происходит.
– Шарики одинаковы по объему и вытесняют одинаковое количество воды. Тяжелый шарик никак жестко не привязан к сосуду с водой. Следовательно вес сосуда, определяется только фактическим объемом воды находящейся в нем и объемом воды вытесняемой шариком. Легкий шарик жестко привязан к донышку сосуда. Шарик полый и на него действует выталкивающая сила, действующая и на сосуд по жесткой связи. Следовательно вес сосуда, определяется фактическим объемом воды находящейся в нем, объемом воды вытесняемой шариком и силой выталкивания, направленной в противоположную сторону. При одинаковом объеме воды, сосуд с легким шариком весит меньше…
– Чаша со стальным шариком перевешивает на величину вес воды вытесненной шариком, остальной вес воспринимает подвес.
3. Система будет в равновесии:
– Равновесие. Железо не давит на рычаг, полый шар почти что тоже, объём воды в одинаковых стаканах одинаков.
– На шарик пинг-понга действует архимедова сила, но она уравновешена натяжением нити, в итоге не влияет на весы. Стальной шарик просто подвешен на внешней опоре и тоже не влияет на весы. Объем шариков не играет роли, даже если они будут разного диаметра это не нарушит равновесия. Главное одинаковый объем воды.
А теперь все же правильный ответ:
Кто объяснит без формул, почему все происходит именно так?
П.С. кстати, пару лет назад, когда я выкладывал эту задачку ответы были вот такие:
Источник
Задачи, тесты
Е. М.
Раводин,
, МОУ СОШ № 2, г. Прокопьевск, Кемеровская обл.
Окончание. См. № 5,
8/2010
18. Прямоугольная коробочка из жести массой m = 76 г с дном площадью S = 38 см2 и высотой H = 6 см плавает в воде. Определите высоту h надводной части коробочки.
Решение. Коробочка плавает, если действующая на неё сила тяжести равна по модулю действующей на неё силе Архимеда: mg = FА, причём FА = Vпчgρв, где – объём погружённой части коробочки. Подставляя числовые данные, получаем
Отсюда глубина погружения коробочки равна
Значит h = H – x = 4 см.
19. Льдина плавает на поверхности пресной воды. Какую часть составляет объём подводной части от объёма всей льдины? Если задача не решается в общем виде, то, для упрощения, примите объём льдины равным 100 м3. Плотность льда 900 кг/м3.
Решение. Раз льдина плавает, то её сила тяжести равна по модулю силе Архимеда: mg = FА, т. е.:
20. На поверхности широкого озера лёд имеет толщину 2 м. Какой минимальной длины надо взять верёвку, чтобы зачерпнуть кружкой воды из проруби?
Решение. Так как озеро широкое, то лёд на его поверхности может только плавать, а не держаться за берега за счёт примерзания к ним. Согласно решению задачи № 19, в проруби под поверхностью воды окажется 0,9 толщи льда, т. е. 0,9 · 2 м = 1,8 м, а над поверхностью воды 0,2 м = 20 см. Для зачерпывания воды с такой глубины верёвка не нужна.
21. В стакане с пресной водой плавает кусок льда. Изменится ли уровень воды, когда лёд растает? Рассмотрите дополнительно случаи: когда в лёд вмёрзла дробинка; когда в лёд вмёрз пузырёк воздуха.
Решение. Лёд плавает, если его вес равен весу жидкости в объёме погружённой части. Образовавшаяся изо льда пресная вода имеет тот же вес, что и лёд, и, следовательно, точно заполнит объём, который вытеснял плавающий лёд. Значит, уровень воды не изменится.
Если во льду была дробинка, лёд вытеснял больше воды, чтобы поддерживать на плаву дробинку. Когда лёд растаял, дробинка утонула (её вес больше веса вытесненной ею воды), уровень воды понизился.
В случае вмёрзшего пузырька уровень воды после таяния льдины практически не изменится. Хотя, если подсчитать точно, уровень воды несколько понизится, т. к. масса воздуха в пузырьке хоть и мала, но не равна нулю.
22. В прямоугольный сосуд с водой пустили плавать модель судна массой m = 4 кг. На сколько при этом повысился уровень воды, если площадь дна сосуда S = 2000 см2?
Решение. Вес сосуда при опускании в него модели увеличится на вес модели mg. Это увеличение веса можно интерпретировать как следствие подъёма уровня воды на ∆h и, следовательно, увеличения силы давления воды ∆Fд = ρвg∆hS. Отсюда:
23. Кусок парафина массой m = 200 г плавает на границе раздела воды и бензина. Определите объём V1 надводной части бруска. Плотность парафина 900 кг/м3, бензина 700 кг/м3.
Решение. Если парафин плавает, то сила тяжести равна сумме сил Архимеда в обеих жидкостях: mg = Vвρвg + V1ρб g, где Vв – объём, погружённый в воду, V1 – искомый надводный объём (в бензине). Общий объём парафина
Решая совместно оба уравнения, получаем:
24. Кусок льда, внутрь которого вморожен шарик из свинца, плавает в цилиндрическом сосуде с водой. Площадь дна сосуда S. Какова масса шарика, если после полного таяния льда уровень воды в сосуде понизился на H? Плотность свинца ρ1, плотность воды ρ2.
Решение. На плавающую льдину со свинцовым шариком действует бóльшая сила Архимеда, чем на такую же льдину без шарика, т. к. она тяжелее на силу тяжести шарика mg. Следовательно, объём вытесняемой в первом случае воды больше, чем во втором, на Но когда льдина растает, шарик упадёт на дно и займёт объём V1 = m/ρ1. Общее уменьшение объёма воды в конечном счёте ∆V = ∆Vп – V1. Так как ∆V = SH (по условию), то приходим к уравнению:
25. Корона царя Гиерона в воздухе весит P1 = 20 Н, а в воде P2 = 18,75 Н. Вычислите плотность вещества короны. Была ли она из чистого золота? Дополнение: найдите, сколько золота и сколько серебра было в короне. Плотность золота округлённо принять 20 000 кг/м3, а серебра 10 000 кг/м3.
Решение. Для оценки добросовестности мастера найдём плотность короны по формуле полученной при решении задачи 9 (см. № 5/2010):
– корона не из чистого золота.
Чтобы найти состав короны, используем два факта: 1) общая масса короны m = mз + mс; 2) общий объём короны V = Vз + Vс (индексы «з» и «с» относятся к золоту и серебру соответственно). Заменяя объёмы их выражениями через массы и плотности, получаем систему из двух уравнений:
Решение
Опуская громоздкие промежуточные вычисления, запишем ответ:
26. Какую силу надо приложить к пробковому телу массой 400 кг, чтобы удерживать его, когда оно целиком погружено в воду? ρп = 200 кг/м3; g = 10 м/с2.
Решение. Сила тяжести тела mg = 4000 Н направлена вниз, сила Архимеда направлена вверх и равна
Чтобы удержать тело в воде, надо приложить направленную вниз силу F = FА – mg = 16 кН.
27. Чугунная плита толщиной 0,5 м, длиной 10 м и шириной 4 м лежит на глинистом дне, выдавив из-под себя воду. Глубина водоёма 2,5 м. Какую силу необходимо приложить, чтобы начать подъём плиты?
Решение. Объём плиты V = 0,5 м · 10 м · 4 м = 20 м3.
Её масса m = Vρч = 20 м3 · 7000 кг/м3 = 140 000 кг.
Сила тяжести mg = 1 400 000 Н.
Поскольку под плитой нет воды, сила Архимеда на неё не действует. Вниз на плиту, кроме силы тяжести, действуют сила давления воды на глубине 2,5 – 0,5 = 2 (м) и сила давления атмосферы, которую передаёт вода по закону Паскаля. При нормальном атмосферном давлении общее давление на плиту:
p = pв + pа = 1,2 · 105 Па.
Горизонтальная площадь поверхности плиты
S = 40 м2. Сила давления на плиту F = pS = 4,8 · 106 Н.
Полная сила, прижимающая плиту к грунту:
F = mg + Fа = 1,4 · 106 Н + 4,8 · 106 Н = 6,2 ·106 Н.
Для отрыва от грунта нужна сила F > 6,2 МН.
Источник
