В сосуде с водой плавает стакан с гирей

Задача по физике – 4962
В сосуде с водой плавает стакан, в котором находится камень. Как изменится уровень воды в сосуде, если из стакана вынуть камень и опустить его в сосуд?
Решение. При перенесении камня в сосуд общий вес воды, камня и стакана не меняется. Площадь дна сосуда тоже не меняется. Следовательно, давление системы трех тел на дно сосуда не должно измениться. Но давление столба воды на дно сосуда $p = rho gh$, где $rho$ – плотность воды, $g$ – ускорение силы тяжести, $h$ – высота столба. Следовательно, уровень воды в сосуде не должен измениться.
Проделаем соответствующий опыт и убедимся, что уровень воды в сосуде понизится. В чем ошибочность решения?
Подробнее
Задача по физике – 4963
В сосуде со ртутью плавает чугунный брусок. Изменится ли положение центра тяжести бруска по отношению к уровню ртути, если в сосуд налить воды?
Решение. Вода давит на брусок сверху и с боков. Силы давления на брусок с боков уравновешиваются, а сила давления на брусок сверху должна понизить положение центра тяжести бруска по отношению к уровню ртути.
Проделаем соответствующий опыт и обнаружим, что брусок в ртути не опускается, а немного всплывает. В чем ошибочность представленного выше решения?
Подробнее
Задача по физике – 4964
Обычно считают, что сифоном можно переливать жидкость из верхнего сосуда в нижний. Если в большой сосуд с водой поместить два сосуда А и В, причем в первом находится керосин, а во втором – вода (рис.), и соединить их трубкой, то керосин будет переливаться из нижнего сосуда А в верхний сосуд В.
Таким образом, керосин, всплывая, увеличивает свою потенциальную энергию по отношению к Земле. Не противоречит ли этот опыт закону сохранения энергии?

Подробнее
Задача по физике – 4965
Кювета с водой стоит на бруске (рис.). На воде плавает коробочка с гирей. Кювета находится в равновесии.
Если вынуть гирю из коробочки и поставить на дно кюветы под тем местом, где плавала коробочка, то равновесие нарушится (рис.), хотя вес левой части кюветы как будто бы не изменился. Объясните ошибку рассуждений

Подробнее
Задача по физике – 4966
Если в установке, изображенной на рисунке, пережечь нить АВ, то тело Р, имеющее объем 100 $см^{3}$, целиком погружается в воду и остается висеть на нити АСВ. При этом равновесие весов нарушается. На какую чашку весов и какой добавочный груз необходимо положить, чтобы восстановить равновесие?
Решение. В соответствии с законом Архимеда тело Р, погруженное в воду, будет выталкиваться вверх с силой 0,98 н. Поэтому на правую чашку весов будет действовать вес штатива и вес тела Р, уменьшенный на вес вытесненной им воды.
Следовательно, для восстановления равновесия весов необходимо на правую чашку поставить гирю массой 100 г.
Однако опыт показывает, что на правую чашку весов необходимо поставить гирю массой 200 г. В чем ошибка решения?

Подробнее
Задача по физике – 4967
Симметричный относительно вертикальной плоскости ОК сосуд ABCD (рис.) наполнен водой и опирается о ребро неподвижной призмы. В правую часть сосуда опустили кусок алюминия массой 0,5 кг, а в левую – кусок свинца массой 0,4 кг. Какая часть сосуда перетянет?
Решение. Сосуд представляет собой сложный равноплечий рычаг. Так как вес куска алюминия больше, чем свинца, то перетянет правая сторона сосуда, где лежит кусок алюминия.
Опыт, однако, опровергает это заключение. В чем ошибка решения?

Подробнее
Задача по физике – 4968
В высокий стеклянный цилиндрический сосуд помещают песочные часы, наливают воды до самого верха и закрывают крышкой (рис.). Часы всплывают под самую крышку. Затем цилиндр переворачивают. Часы не всплывают (рис.), хотя они окружены водой и выталкивающая сила больше веса часов. Через определенный промежуток времени, когда некоторое количество песка высыплется в нижнее отделение, часы начнут медленно всплывать. Таким образом, перетекание песка из верхнего отделения часов в нижнее влияет на его плавучесть. Но ведь часы герметически закрыты и вес их от перетекания песка не изменяется. Как объяснить этот парадокс?

Подробнее
Задача по физике – 4969
Взлет космического корабля с Земли происходит с ускорением, в несколько раз превышающим ускорение силы тяжести. Поэтому находящийся в корабле космонавт подвергается действию перегрузки (силы, прижимающей человека к опоре).
Чтобы избежать перегрузки, предлагают помещать космонавта в камеру с водой (плотность воды примерно равна плотности человеческого тела). Авторы проекта считали, что человек, находясь в воде, становится невесомым и, следовательно, совершенно избавляется от действия как естественной, так и искусственной тяжести (перегрузки). В чем состоит ошибка такого заключения?
Подробнее
Задача по физике – 4970
Рассмотрим один из проектов вечного двигателя. В вырез стенки АВ бака с жидкостью вставлен вал (рис.), ось которого О лежит в плоскости стенки АВ. Вал закрывает собой весь вырез, так что жидкость не выливается; вал может вращаться на своей оси. На половину вала, погруженную в жидкость, по закону Архимеда действует подъемная сила, которая, по мысли изобретателя, должна вызвать вращение вала против часовой стрелки. Это вращение должно было бы продолжаться вечно. В чем ошибка проекта?

Подробнее
Задача по физике – 4971
Швейцарец Г. Леонард в 1865 г. предложил следующий проект вечного двигателя. Бесконечная цепь из жестяных поплавков проходит правой половиной сквозь сосуд В с водой (рис.). По мысли автора, поплавки, стремясь всплыть, будут вращать колесо С, через которое эта цепь переброшена, против движения часовой стрелки. В чем ошибка проекта?

Подробнее
Задача по физике – 4972
В XV в. был предложен проект вечного двигателя, основанный на законе Архимеда. В проекте этого вечного двигателя имеется колесо с семью откидывающимися на шарнирах грузами (рис.). Изобретатель погрузил одну треть колеса в воду, обоснованно предполагая, что вес этой части колеса и грузов уменьшится по известному закону Архимеда и колесо придет во вращение. В чем ошибка проекта?

Подробнее
Задача по физике – 4973
Шар движется в воздухе, имея в данный момент скорость $v$ (рис.). Так как сила сопротивления воздуха пропорциональна квадрату скорости, то ее можно представить в виде $F = kv^{2}$, где $k$ – коэффициент пропорциональности.
С другой стороны, разложив скорость $v$ на горизонтальную и вертикальную составляющие, получим: $v_{1} = v cos 60^{ circ}$ и $v_{2} = v sin 60^{0}$. Следовательно, $F_{1} = kv_{1}^{2} = kv^{2} cos^{2} 60^{ circ}$ и $F_{2} = kv_{2}^{2} = kv sin^{2} 60^{ circ}$, где $F_{1}$ и $F_{2}$ – силы сопротивления, вызванные составляющими $v_{1}$ и $v_{2}$. Таким образом, полная сила сопротивления равна:
$F = sqrt{ F_{1}^{2} + F_{2}^{2}} = sqrt{(kv^{2} cos^{2} 60^{ circ}) + (kv^{2} sin^{2} 60^{ circ})} = kv^{2} sqrt{ frac{5}{8}}$
что не совпадает с выражением $F=kv$. Как разрешить это противоречие?

Подробнее
Задача по физике – 4974
Все тела падают на землю. Облака состоят из мелких капелек воды. Значит, облака должны падать на землю.
Однако никому не удавалось наблюдать, чтобы облако, опускаясь, когда-нибудь достигло земли. Как разрешить этот парадокс?
Подробнее
Задача по физике – 4975
При испытании реактивного снаряда, установленного в хвосте самолета для его защиты от нападения сзади, был обнаружен удивительный парадокс. При выпуске снаряда он сначала удалялся от самолета, а затем разворачивался и догонял самолет. Как можно объяснить это явление?
Подробнее
Задача по физике – 5135
В одном из солёных озёр Канады плотность воды зависит от глубины так, как показано на рис. На какой глубине и в каком положении будет плавать тонкая однородная палка? Плотность материала, из которого она сделана, равна 1020 $кг/м^{3}$.

Подробнее
Источник
Решебник
ВСЕ
ФИЗИКА
МАТЕМАТИКА
ХИМИЯ
Задача по физике – 75
В большом сосуде с водой плавает в вертикальном положении тонкостенный стакан, в который налито некоторое количество воды. Разность уровней воды в сосуде и стакане равна х. Как изменится эта разность, если в стакан опустить пробку?
Подробнее
Задача по физике – 76
Толстостенная лодка с вертикальными стенками и отверстием в дне достаточно долго свободно плавает в озере. Затем отверстие снаружи затыкают и внутрь лодки опускают бревно. Повысится или понизится после этого уровень воды в лодке относительно уровня воды в озере? Почему?
Подробнее
Задача по физике – 77
Шайба массой М, имеющая форму цилиндра с площадью основания S и высотой h, плавает на границе раздела двух несмешивающихся жидкостей с плотностями $rho_{1}$ и $rho_{2}$ ($rho_{1}
Подробнее
Задача по физике – 78
Кубик плавает в сосуде с водой так, что его верхняя грань параллельна поверхности воды. При этом половина кубика погружена в воду. Какой слой масла надо долить, чтобы кубик плавал полностью погруженным в жидкость, если плотность масла в два раза меньше плотности воды и длина ребра кубика равна а? Масло с водой не смешивается.
Подробнее
Задача по физике – 79
Вес Р системы, состоящей из стакана с водой и пробкового шарика, измеряется в пяти случаях:
1) шарик свободно плавает в стакане (показание весов $P_{1}$);
2) шарик лежит на чаше весов рядом со стаканом ($P_{2}$);
3) шарик удерживается в полностью погруженном состоянии тонкой невесомой нитью, прикрепленной ко дну стакана ($P_{з}$);
4) шарик удерживается в полностью погруженном состоянии тонкой невесомой спицей, закрепленной над стаканом ($P_{4}$);
5) * шарик, удерживавшийся в утопленном состоянии, освобождается и начинает свободно всплывать ($P_{5}$).
Расставьте показания весов в порядке их возрастания.
Подробнее
Задача по физике – 80
На чашке весов стоят гиря и стакан с водой. Сравните показание весов Р с показаниями весов в следующих случаях:
1) гиря подвешена на нити к внешнему штативу и погружена в воду ($P_{1}$);
2) * подвес оборвался, и гиря начинает тонуть ($P_{2}$).
Подробнее
Задача по физике – 81
Пробка прикреплена посредством легкой пружинки к дну сосуда с водой. И пробка и пружинка полностью погружены в воду. Увеличится или уменьшится длина пружинки, если сосуд начнет двигаться вертикально вверх (вниз) с постоянным ускорением?
Подробнее
Задача по физике – 82
В сосуд с водой опущена труба диаметром d.В трубу поместили шарик того же диаметра. Центр шарика оказался на глубине h. Найдите плотность вещества шарика. Зазор между трубой и шариком отсутствует. Сила трения между ними равна нулю.
Подробнее
Задача по физике – 83
Раковина в ванной комнате имеет сливное отверстие радиусом r. В раковину опускают шар массой m и радиусом R > r и начинают медленно наливать воду. Опишите качественно дальнейшее поведение системы в зависимости от соотношения между m, R, r.
Подробнее
Задача по физике – 84
Шарик, плотность которого меньше плотности волы, с помощью тонкой нити прикреплен к дну большого сосуда, заполненного водой. Сосуд движется вправо с ускорением а. В какую сторону и на какой угол $alpha$; отклонена нить от вертикали?

Подробнее
Задача по физике – 85
На горизонтальной плоскости лежит капля ртути объемом V. Сверху на каплю поставили брусок массой М так, что капля сильно сплющилась (рис.). Оцените расстояние h между бруском и плоскостью, если коэффициент поверхностного натяжения ртути $omega$ и все поверхности абсолютно не смачиваются ртутью.
Подробнее
Задача по физике – 86
Металлическая иголка диаметром d = 1 мм и длиной $l ll d$ смазана жиром так, что ее поверхность абсолютно не смачивается водой. Найдите максимально возможную плотность $rho$ вещества иголки. при которой она не будет тонуть в воде. Коэффициент поверхностного натяжения воды а принять равным 0,07 Н/м, а ускорение свободного падения $g = 10 м/с^{2}$ .
Подробнее
Задача по физике – 87
Шарик массой m, подвешенный на невесомой нерастяжимой нити вращается по окружности вокруг вертикальной оси с постоянной угловой скоростью $omega$ (эта система носит название “конический маятник, рис. а). Где нить конического маятника должна быть прочнее – на Земле или на Луне?

Подробнее
Задача по физике – 88
Два одинаковых массивных шарика скреплены невесомой пружиной. Шарики летят с одинаковой скоростью v, как показано на рис. а. Сила тяжести отсутствует. Как будут двигаться шарики после столкновения со стенкой, если удар о стенку абсолютно упругий и время удара шарика о стенку много меньше периода собственных колебаний системы?

Подробнее
Задача по физике – 89
Малое тело массой $m = 10 г$ подвешено на нити AB к пружине с жесткостью $k = 10 кг/с^{2}$ (рис.). Пружина и нить невесомы, нить нерастяжима. Система совершает гармонические колебания в вертикальном направлении в поле тяжести. Может ли амплитуда А этих колебаний быть равна 1 см?
Подробнее
Источник
А так ли хорошо знакома вам гидроаэростатика? // Квант. – 2011. – № 3. – C. 32
По специальной договоренности с редколлегией и редакцией журнала “Квант”
• …доказано, что более легкие, чем жидкость, тела, будучи
насильно погружены в эту жидкость, движутся вверх с
силой, равной тому весу, на который жидкость, имеющая
объем, равный этому телу, будет тяжелее последнего.
Архимед
Мы погружены на дно безбрежного моря воздушной
стихии, которая, как известно из неоспоримых опытов,
имеет вес, причем он наибольший вблизи поверхности
Земли…
Эванджелиста Торричелли
Сосуд, наполненный водой, является новым принципом
механики и новой машиной для увеличения сил в
желаемой степени…
Блез Паскаль
…Полет на свободном аэростате представляет нечто
совершенно исключительное.
Камиль Фламмарион
Это и есть уравнение гидростатики. В общем случае оно
не имеет решения.
Ричард Фейнман
Безбрежное небо и неведомые глубины океана всегда влекли человека, побуждая его подняться как можно выше в воздух и опуститься как можно глубже под воду. Более двух тысяч лет назад был установлен один из самых древних законов, с которым вы знакомитесь одним из самых первых в курсе школьной физики, – закон Архимеда. С тех пор можно отсчитывать начало научного освоения двух стихий и рождение гидроаэростатики.
Мысли выдающихся ученых – как верстовые столбы на пути понимания и применения этого закона. Полеты на огромные высоты и глубоководные погружения совершаются сегодня на аппаратах, оснащенных современнейшим оборудованием, не только ради рекордов. Исследования атмосферы, в том числе последствий глобального потепления, разведка с воздуха, доставка грузов в труднодоступные места, совершенствование надводного и подводного флота, изучение морской фауны и флоры, поиски полезных ископаемых под океанским дном – вот неполный список задач, для решения которых необходимы аэростаты и дирижабли, научные суда и батискафы и… лежащий в основе их работы добрый старый закон Архимеда.
Но и в более простых задачах можно обнаружить неожиданные «подводные камни». Однако, не боясь предупреждения Фейнмана, беритесь за них – решения обязательно найдутся!
Вопросы и задачи
- Что изображено на приведенном здесь рисунке? А если его перевернуть?
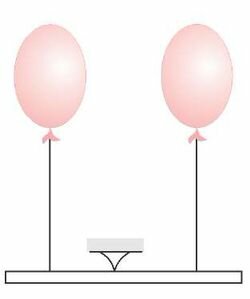
- Два сплошных цилиндра одинаковой массы и равного диаметра, но один алюминиевый, а другой свинцовый, плавают в вертикальном положении в ртути. Какой из них погружен глубже?
- В двух одинаковых сосудах с водой плавают плоская широкая и высокая узкая коробочки. Когда в каждую из них положили по одинаковому тяжелому грузику, они остались на плаву. В каком из сосудов уровень воды при этом поднялся выше?
- Стакан с наклонными стенками, наполненный водой до краев, взвешивают на весах. Затем взвешивают этот же стакан с опущенным в него деревянным бруском, плавающим так, что вода доходит до краев стакана. Отличаются ли показания весов?
- В ведре, наполненном доверху водой, плавает дырявая кастрюля. Выльется ли часть воды из ведра, когда кастрюля утонет?
- Купаясь в речке с илистым дном, можно заметить, что ноги больше вязнут в иле на мелких местах, чем на глубоких. Как это можно объяснить?
- Для погружения на 10 метров подводная лодка набирает в себя 100 тонн воды. А сколько воды ей надо набрать, чтобы погрузиться на 100 метров?
- Стальной шарик плавает в ртути. Увеличится или уменьшится глубина его погружения, если повысить температуру?
- Вес жидкости, налитой в сосуд, равен 3 Н. В жидкость погружают тело. Может ли архимедова сила, действующая на тело, равняться 10 Н?
- В двух одинаковых сосудах на поверхности воды плавают одинаковые пробковые цилиндры, к которым снизу на тонких нитях привязаны одинаковые грузы, причем один груз находится в воде, а другой лежит на дне сосуда. Одинаков ли вес сосудов со всем, что в них находится?
- В сосуде с водой плавает кусок льда, удерживаемый натянутой нитью, прикрепленной к дну сосуда. Как изменится уровень воды в сосуде, когда лед растает?
- Порожнюю закрытую бутылку (с плоским дном) погружают в воду один раз горлышком вниз, а другой раз горлышком вверх на одну и ту же глубину, равную половине высоты бутылки. В каком случае совершается большая работа?
- Вес любого тела на экваторе примерно на полпроцента меньше, чем в северных широтах. Изменяются ли осадка судна и его грузоподъемность при переходе из Северного Ледовитого океана в экваториальные воды? Плотность морской воды считайте везде одинаковой.
- Со дна высокого стеклянного сосуда, наполненного водой, поднимается небольшой пузырек воздуха. Как изменяется выталкивающая его сила? Каков характер движения пузырька?
- Из какого материала надо сделать гири, чтобы при точном взвешивании можно было не вводить поправки на уменьшение веса в воздухе?
- Одинаковые по массе оболочки двух шаров сделаны из разных материалов: одна – из эластичной резины, другая – из прорезиненной ткани. Оболочки шаров наполнили водородом одного и того же объема и отпустили в воздухе. Какой из шаров поднимется на большую высоту?
- Как зависит подъемная сила аэростата или дирижабля от температуры, при которой производится полет?
- Чтобы дирижабль мог взлететь, его наполняют газом, более легким, чем воздух. Не лучше ли совсем выкачать из него газ?
- Почему воздушный шар с закрытым выпускным клапаном, поднявшись на большую высоту, может лопнуть?
- На дне сосуда с газом лежит тело, плотность которого немного больше плотности газа. Можно ли, повышая давление газа, заставить тело подняться вверх?
Микроопыт
В аквариум прямоугольной формы, наполненный водой, поместите любое тело, которое будет в нем плавать. Можно ли определить массу этого тела без взвешивания?
Любопытно, что…
…хотя Архимед считал себя прежде всего теоретиком, а работу над практическими приложениями относил к деятельности второго сорта, с его именем связывают около 40 изобретений.
…утверждение, получившее в науке имя Паскаля и ставшее одним из основных законов гидростатики, возможно, не в столь явной форме обнаруживается в трудах и Леонардо да Винчи, и Стевина, и Галилея, и Торричелли.
…несмотря на свою историческую важность, закон Архимеда не относится к фундаментальным законам природы. Так, его можно считать прямым следствием закона Паскаля; Стевин довольно просто обосновал его, исходя из принципов равновесия с помощью так называемого метода отвердевания жидкости; закон Архимеда выводится также из закона сохранения энергии.
…чтобы доказать, что пространство над столбиком ртути – в знаменитом опыте с заполненной ею стеклянной трубкой – остается пустым, Торричелли впускал туда воду, которая под действием атмосферного давления врывалась в него «со страшным напором» и целиком его заполняла.
…неосознанно, не пользуясь расчетами, люди издревле опирались на закон Архимеда, когда, например, необходимо было преодолевать водные преграды. И лишь в 1666 году английский корабел Энтони Дин, к удивлению современников, теоретически определил осадку корабля и прорезал в его бортах отверстия для пушек до его спуска на воду, в то время как раньше это проделывали, когда корабль был уже на плаву.
…к основоположникам аэростатики справедливо причисляют и Роберта Бойля, именем которого назван известный газовый закон. Так, после усовершенствования им насоса для откачки воздуха из резервуаров большого объема тут же возникли проекты по созданию летательных аппаратов, «более легких, чем воздух», причем сразу же предусматривались военные применения таких машин.
…полет людей на воздушном шаре, заполненном горячим дымом, долго не позволял совершить братьям Монгольфье сам французский король, опасаясь за жизнь аэронавтов. Первый полет был осуществлен лишь в 1783 году. И в том же 1783 году (в год своей смерти) великий математик Леонард Эйлер подробно рассчитал подъемную силу аэростата, словно завещал разумно рисковать, опираясь на знания законов физики.
…в 1932 году швейцарский физик Огюст Пикар поднялся на аэростате собственной конструкции в стратосферу на высоту почти 17 километров, а позднее на разработанном им же батискафе погрузился в самую глубокую точку Средиземного моря. В 1960 году его сын Жак на батискафе «Триест» погрузился в Марианскую впадину на рекордную глубину около 11 тысяч метров. Семейную традицию поддержал внук Огюста Пикара – Бертран, совершивший в 1999 году кругосветное путешествие на воздушном шаре «Орбитер» за двадцать дней без промежуточной посадки.
…автор модели расширяющейся Вселенной Александр Фридман занимался еще и метеорологией и в 1925году принял участие в рекордном по тому времени полете на воздушном шаре до высоты 7400 метров. А Огюст Пикар, научным руководителем которого был автор теории относительности Альберт Эйнштейн, поднимался в небо на аэростате в том числе и для проведения эксперимента, подтвердившего эту теорию.
…на смену людям, совершающим глубоководные погружения в батискафах, приходят роботы, «одетые» в специальную керамическую оболочку, позволяющую выдерживать чудовищное давление. Так, в 2009 году американский робот «Нерей» провел на дне Марианского желоба десять часов, выполняя различные измерения.
Ответы
- Равновесие воздушных шаров. На перевернутом рисунке -равновесие сосудов с жидкостью.
- Имея равный вес, цилиндры вытесняют одинаковые объемы ртути, а так как диаметры их равны, то одинаковы и глубины погружения.
- Объем погруженной в воду части каждой коробочки меняется на одну и ту же величину. Поскольку сосуды одинаковы, то и уровень воды в каждом из них повысится одинаково.
- Нет, так как вес вытесненной бруском воды равен весу бруска.
- Нет, не выльется. Плотность материала кастрюли больше плотности воды, поэтому когда кастрюля утонет, она будет вытеснять меньший объем, нежели когда она плавала. Значит, уровень воды в ведре понизится.
- На мелководье меньше действующая на человека выталкивающая сила.
- Практически столько же, так как воду при погружении на такие глубины можно считать несжимаемой.
- При нагревании ртуть расширяется сильнее, чем сталь, поэтому выталкивающая сила уменьшится, и шарик опустится глубже.
- Да, может, если размеры тела близки к размерам сосуда.
- Во втором сосуде пробковый цилиндр погрузился меньше, чем в первом, т.е. вытеснил меньше воды. Следовательно, второй сосуд тяжелее первого.
- Допустим, что нить оборвалась. Тогда лед всплывет, и уровень воды в сосуде понизится. При дальнейшем таянии льда уровень воды уже меняться не будет.
- Во втором, так как у бутылки внешний объем нижней части всегда больше объема верхней части.
- Не изменяются, поскольку в весе одновременно теряют и судно, и вытесняемая им вода.
- По мере поднятия увеличивается объем пузырька. Выталкивающая сила, пропорциональная объему пузырька, будет расти. На пузырек также будет действовать сила сопротивления, но она пропорциональна площади сечения пузырька и поэтому будет возрастать медленнее. Значит, движение пузырька будет ускоренным.
- Гири нужно сделать из того же материала, что и взвешиваемое тело.
- На одной и той же высоте над землей у шара из эластичной резины объем будет больше, чем у шара из прорезиненной ткани. Значит, выталкивающая сила, действующая на него, будет больше, и он поднимется выше.
- Чем больше разница в плотностях воздуха и газа, заполняющего аэростат или дирижабль, тем больше подъемная сила. Следовательно, она возрастает при понижении температуры воздуха, когда он становится плотнее.
- Дирижабль без газа внутри, конечно, стал бы легче, но его раздавило бы давление наружного воздуха.
- Оболочка шара может не выдержать разности внутреннего и уменьшившегося внешнего давлений.
- В принципе, можно – если сжимаемость газа больше сжимаемости тела.
Микроопыт
Можно. Для этого достаточно найти объем вытесненной телом воды, измерив сечение аквариума и изменение уровня воды при опускании в нее тела, и затем умножить этот объем на плотность воды.
Что читать в «Кванте» о гидроаэростатике
(публикации последних лет)
- «Как попасть на Таинственный остров» – 2004, №1, с. 25;
- «Путешествие на воздушном шаре» – 2004, №3, с.31;
- «Задачи с жидкостями» – 2006, №1, с.40;
- «Вверх и вниз через атмосферу» – 2007, №1, с.9;
- «Гидростатика в стакане» – 2008, №3, с.47;
- «Устоит ли наш кораблик?» – 2008, №4, с.42;
- «Силы сопротивления в задачах динамики» – 2009, №1, с.50;
- «Подводные камни» силы Архимеда» – 2009, №2, с.46;
- «О плавании одномерных объектов» – 2010, №4, с.36.
Материал подготовил А.Леонович
Источник
