В сосуде с водой в вертикальном положении плавает тонкий
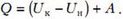
- Главная
- Вопросы & Ответы
- Вопрос 3611171
Мари Умняшка
более месяца назад
Просмотров : 35
Ответов : 1
Лучший ответ:
Зачетный Опарыш
A = (0 + mg)x/2 = ρ2gH2(1 − Sц/S) = 360 мДж.
более месяца назад
Ваш ответ:
Комментарий должен быть минимум 20 символов
Чтобы получить баллы за ответ войди на сайт

Лучшее из галереи за : неделю месяц все время































Другие вопросы:
Главный Попко
Проверьте пожалуйста друзья Понижающий трансформатор с коэффициентом трансформации k=24 включен в сеть переменного тока с действующим напряжением Uд1=220 В. Определите действующее значение силы тока Iд1 в первичной обмотке трансформатора и тепловые потери мощности P2 в его вторичной обмотке, если а…
более месяца назад
Смотреть ответ
Просмотров : 17
Ответов : 1
Пармезан Черница
Помогите пожалуйста, с домашним тестом по литературе Акакий Акакиевич Башмачкин, герой повести Н.В. Гоголя «Шинель», мечтал Выберите один ответ: 1. о повышении в должности 2. о власти 3. о богатстве 4. о другом
более месяца назад
Смотреть ответ
Просмотров : 6
Ответов : 1
Энджелл
Количество мономеров в ДНК
более месяца назад
Смотреть ответ
Просмотров : 9
Ответов : 1
Таня Масян
В треугольнике ABC угол C равен 90°, AC=12, BC=9. Найдите cosA
более месяца назад
Смотреть ответ
Просмотров : 16
Ответов : 1
Зачетный Опарыш
Помогите, пожалуйста! Помогите составить задачу на уравнение 3x-2x=18
более месяца назад
Смотреть ответ
Просмотров : 13
Ответов : 1
Источник
- Главная
- Вопросы & Ответы
- Вопрос 8227203
Зачетный Опарыш
более месяца назад
Просмотров : 3
Ответов : 1
Лучший ответ:
Энджелл
A = (0 mg)x/2 = ρ2gH2(1 − Sц/S) = 360 мДж.
более месяца назад
Ваш ответ:
Комментарий должен быть минимум 20 символов
Чтобы получить баллы за ответ войди на сайт

Лучшее из галереи за : неделю месяц все время































Другие вопросы:
Васян Коваль
Построить Б53 и Мdur7 от “до” в четырёхголосии во всех мелодических положениях в тесном и широком расположении.
более месяца назад
Смотреть ответ
Просмотров : 2
Ответов : 1
Энджелл
какие животные обитают а заповеднике “остров врангеля”
более месяца назад
Смотреть ответ
Просмотров : 2
Ответов : 1
Картинок: 1
Главный Попко
кроссворд импровизация
более месяца назад
Смотреть ответ
Просмотров : 2
Ответов : 1
Главный Попко
Сообщение на тему “Как люди хранили скоропортящиеся продукты, когда не было холодильников?”
более месяца назад
Смотреть ответ
Просмотров : 2
Ответов : 1
Суррикат Мими
Представь, что ты живёшь в доме из металла. Что будет основным недостатком такого жилья?
более месяца назад
Смотреть ответ
Просмотров : 2
Ответов : 1
Источник
Óñëîâèÿ çàäà÷
Ãèäðîñòàòèêà.
1201.
Ñîñóä ñ âîäîé óðàâíîâåøåí íà îäíîé èç ÷àøåê ðû÷àæíûõ âåñîâ.  ñîñóä
îïóñêàþò ïîäâåøåííûé íà íèòè ìåòàëëè÷åñêèé áðóñîê ìàññîé
m òàê, ÷òî îí îêàçûâàåòñÿ ïîëíîñòüþ
ïîãðóæåííûì â âîäó, íî íå êàñàåòñÿ ñòåíîê è äíà ñîñóäà. Êàêîé ãðóç è íà
êàêóþ ÷àøêó âåñîâ íàäî ïîëîæèòü, ÷òîáû âîññòàíîâèòü ðàâíîâåñèå?
Ïëîòíîñòü ìåòàëëà rì,
âîäû râ.
ðåøåíèå
1202.
Êîëåíà U-îáðàçíîãî ñîñóäà óäàëåíû äðóã
îò äðóãà íà l = 15 ñì. Íàéäèòå
ìàêñèìàëüíóþ ðàçíîñòü óðîâíåé âîäû â íèõ, åñëè ñîñóä äâèæåòñÿ ñ
ãîðèçîíòàëüíûì óñêîðåíèåì à = 6 ì/ñ2.
ðåøåíèå
1203.
 ñòàêàí, íàïîëîâèíó çàïîëíåííûé æèäêîñòüþ ïëîòíîñòüþ
r, îïóñêàþò óäåðæèâàåìûé â
âåðòèêàëüíîì ïîëîæåíèè öèëèíäð, ïî âûñîòå ðàâíûé âûñîòå ñòàêàíà. Öèëèíäð
îêàçûâàåòñÿ â ðàâíîâåñèè, êîãäà îò åãî íèæíåãî êðàÿ äî äíà îñòàåòñÿ
÷åòâåðòü âûñîòû ñòàêàíà. ×åìó ðàâíà ïëîòíîñòü ìàòåðèàëà öèëèíäðà, åñëè
åãî ñå÷åíèå S, à ñå÷åíèå ñòàêàíà
So?
Òðåíèÿ íåò. ðåøåíèå
1204.
Ñîñóä ñ âîäîé óðàâíîâåøåí íà âåñàõ. Ñîõðàíèòñÿ ëè ðàâíîâåñèå, åñëè
îïóñòèòü ïàëåö â âîäó, íå êàñàÿñü ïðè ýòîì äíà ñîñóäà?
ðåøåíèå
1205.
 ñîñóäå íàõîäÿòñÿ äâå íåñìåøèâàþùèåñÿ æèäêîñòè ðàçëè÷íûõ ïëîòíîñòåé. Íà
ãðàíèöå ðàçäåëà æèäêîñòåé ïëàâàåò îäíîðîäíûé êóáèê, öåëèêîì ïîãðóæåííûé
â æèäêîñòü. Ïëîòíîñòü r
ìàòåðèàëà êóáèêà áîëüøå ïëîòíîñòè r1
âåðõíåé æèäêîñòè, íî ìåíüøå ïëîòíîñòè
r2 íèæíåé æèäêîñòè (r1
< r <
r2). Êàêàÿ ÷àñòü
îáúåìà êóáèêà áóäåò íàõîäèòüñÿ â âåðõíåé æèäêîñòè?
ðåøåíèå
1206. Òîíêàÿ îäíîðîäíàÿ ïàëî÷êà øàðíèðíî óêðåïëåíà çà âåðõíèé êîíåö.
Íèæíÿÿ ÷àñòü ïàëî÷êè ïîãðóæåíà â âîäó (r
= 1000 êã/ì3). Ïðè ýòîì ðàâíîâåñèå äîñòèãàåòñÿ òîãäà, êîãäà
ïàëî÷êà ðàñïîëîæåíà íàêëîííî ê ïîâåðõíîñòè âîäû è â âîäå íàõîäèòñÿ 2/3
÷àñòè ïàëî÷êè. Îïðåäåëèòå ïëîòíîñòü ïàëî÷êè?
ðåøåíèå
1207.
Òåëî â ôîðìå öèëèíäðà ïëàâàåò â âîäå â âåðòèêàëüíîì ïîëîæåíèè, áóäó÷è
ïîãðóæåííûì â íåå íà 80 % ñâîåãî îáúåìà. Êàêàÿ ÷àñòü òåëà áóäåò
ïîãðóæåíà â âîäó, åñëè ïîâåðõ íåå íàëèòü ñëîé áåíçèíà ïîëíîñòüþ
çàêðûâàþùèé òåëî? Ïëîòíîñòü âîäû 1000 êã/ì3, ïëîòíîñòü
áåíçèíà 700 êã/ì3.
ðåøåíèå
1208.
 áàê äèàìåòðîì d = 0,2 ì íàëèòî
m1 = 40 êã âîäû è áðîøåí êóñîê
ëüäà ìàññîé m2 = 9 êã ñ
ïðèìåðçøèì êàìíåì ìàññîé m3
= 0,9 êã. Ïëîòíîñòü âîäû r1
= 1000 êã/ì3, ëüäà r2
= 900 êã/ì3, êàìíÿ r3
= 3000 êã/ì3. Îïðåäåëèòå óðîâåíü âîäû â áàêå ïîñëå òàÿíèÿ
ëüäà. ðåøåíèå
1209.
 áàê äèàìåòðîì d = 0,2 ì íàëèòî
m1 = 60 êã âîäû è áðîøåí êóñîê
ëüäà ìàññîé m2 = 9 êã ñ
ïðèìåðçøèì ïåíîïëàñòîì ìàññîé m3
= 0,3 êã. Ïëîòíîñòü âîäû r1
= 1000 êã/ì3, ëüäà r2
= 900 êã/ì3, ïåíîïëàñòà r3
= 100 êã/ì3. Îïðåäåëèòå óðîâåíü âîäû â áàêå ïîñëå òàÿíèÿ ëüäà.
ðåøåíèå
1210. Îòêðûòàÿ öèñòåðíà ñ âîäîé ñòîèò íà ðåëüñàõ, ïî êîòîðûì ìîæåò
äâèãàòüñÿ áåç òðåíèÿ. Ìàññà öèñòåðíû M,
ìàññà âîäû m. Ñâåðõó â öèñòåðíó íà
ðàññòîÿíèè l îò åå öåíòðà ïàäàåò
âåðòèêàëüíî ãðóç ìàññîé m.
 êàêóþ ñòîðîíó è íà ñêîëüêî ñäâèíåòñÿ öèñòåðíà ê òîìó âðåìåíè, êîãäà
äâèæåíèå âîäû óñïîêîèòñÿ è ãðóç áóäåò ïëàâàòü?
ðåøåíèå
ñëåäóþùàÿ äåñÿòêà
>>>
Источник
Можаев В. Задачи с жидкостями //Квант. — 2006. — № 1. — С. 40-43.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
В этой статье будут рассмотрены задачи, в которых жидкость, с одной стороны, является средой, где находятся твердые тела, а с другой стороны, она, как жидкий элемент, участвует в движении, подобно твердому телу. Наиболее сложными являются комбинированные задачи, в которых жидкость движется вместе с находящимся в ней твердым телом (например, разобранная ниже задача 6).
Перейдем к обсуждению конкретных задач.
Задача 1. В цилиндрический сосуд с водой опустили кусок льда, в который вморожен осколок стекла. При этом уровень воды в сосуде поднялся на h = 11 мм, а лед остался на плаву, целиком погрузившись в воду. На сколько опустится уровень воды в сосуде после того, как весь лед растает? Плотность воды ρв = 1 г/см3, плотность льда ρл = 0,9 г/см3, стекла ρст = 2,0 г/см3
Обозначим первоначальный объем льда через Vл, а объем стекла — через Vст. Когда кусок льда полностью погрузился в воду, он вытеснил объем воды, равный
Очевидно, что этот же объем равен
где S — площадь поперечного сечения сосуда.
Теперь запишем условие плавания куска льда с вмороженным осколком стекла — суммарная сила тяжести льда и стекла равна выталкивающей силе:
Из совместного решения полученных уравнений найдем объемы льда и стекла:
Из растаявшего льда образовалась вода объемом
Поскольку кусок стекла остается в воде, понижение уровня воды в сосуде за время таяния льда будет равно
Задача 2. В вертикально расположенной трубке — с открытым верхним концом, с постоянным внутренним сечением и длиной 3L = 1080 мм — столбиком ртути длиной L заперт слой воздуха такой же длины. Какой длины столб ртути останется в трубке, если ее перевернуть открытым концом вниз? Внешнее давление p0 = 774 мм рт. ст.
Обозначим давление воздуха под ртутным столбиком в исходном положении трубки через p1. Тогда условие равновесия столбика ртути длиной L запишется в виде
где ρ – плотность ртути. Предположим, что после переворота трубки и установления первоначальной температуры часть ртути выльется. Обозначим через h длину столбика оставшейся в трубке ртути. Новое условие равновесия будет иметь вид
где p2 – новое давление воздуха над ртутным столбиком.
Условие сохранения количества изолированного воздуха позволяет записать
Подставляя сюда p1 из первого равенства, а p2 – из второго, получим уравнение относительно h:
или, если записать атмосферное давление в виде , где H0 = 774 мм:
Для данных численных значений L и H0 (в мм) получается, что
h = 270 мм.
Задача 3. U–образная трубка расположена вертикально и заполнена жидкостью. Один конец трубки открыт в атмосферу, а другой конец соединен с сосудом объемом V0 = 0,1 л, заполненным гелием (рис. 1). Объем всей трубки равен объему этого сосуда. В некоторый момент гелий начинают медленно нагревать. Какое минимальное количество теплоты необходимо подвести к гелию, чтобы вся жидкость вылилась из трубки? Атмосферное давление p0 = 105 Па; длины трех колен трубки одинаковы; давление, создаваемое столбом жидкости в вертикальном колене, равно p0/8.
Рис. 1
Обозначим полную длину трубки через 3L, а площадь внутреннего поперечного сечения трубки – S. Поскольку объем трубки V0, то длина каждого колена
Весь процесс нагрева гелия можно разбить на три участка. Первый участок — это когда жидкость еще находится в левом вертикальном колене. Рассмотрим момент времени, когда уровень жидкости в левом колене переместился на величину z, . Из условия равновесия жидкости в трубке найдем давление гелия:
где ρж – плотность жидкости. На втором участке, для которого , давление гелия
а на третьем участке, для
На рисунке 2 изображен график зависимости давления гелия от его объема V, который связан со смещением z простым соотношением:
На первых двух участках тепло необходимо подводить к гелию — это однозначно: здесь газ, расширяясь, совершает работу и одновременно нагревается. А вот третий участок неоднозначен: здесь газ также совершает работу, но при этом он может и охлаждаться. Убедимся, что и на этом участке тепло тоже подводится.
Учитывая, что , запишем уравнение процесса для третьего участка в виде
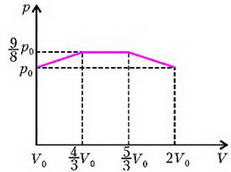
Рис. 2.
Рассмотрим малое изменение объема ΔV. Тогда работа, совершенная гелием, равна
Запишем уравнение состояния гелия как идеального газа:
где ν – количество вещества, Т – температура газа. Подставим в это уравнение выражение для давления на третьем участке процесса и получим
Продифференцируем обе части этого уравнения:
Теперь найдем изменение внутренней энергии гелия при изменении объема на ΔV:
Согласно первому началу термодинамики, подведенное количество теплоты равно сумме изменения внутренней энергии газа и совершенной им работы:
Легко убедиться, что при и
Итак, на всех участках тепло подводится, поэтому полное подведенное к гелию количество теплоты Q найдем как сумму полного изменения внутренней энергии и полной работы, которую совершил гелий:
Поскольку начальная и конечная температуры равны, соответственно,
то изменение внутренней энергии равно
Полную работу найдем как площадь под кривой на рисунке 2:
Тогда окончательно
Задача 4. «Тройник» с двумя открытыми в атмосферу вертикальными трубками и одной закрытой (горизонтальная трубка) полностью заполнен водой (рис. 3). После того, как тройник начали двигать по горизонтали в плоскости рисунка влево с некоторым постоянным ускорением, из него вылилась 1/16 массы всей воды. Чему при этом стало равно давление в жидкости у закрытого конца – в точке А? Трубки имеют одинаковые внутренние сечения. Длину L считать заданной. Диаметр трубок мал по сравнению с длиной L.
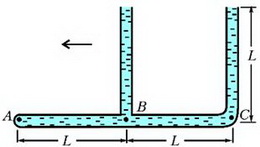
Рис. 3.
При движении тройника влево с ускорением а гидростатические давления в точках А, В и С (см. рис. 3) связаны между собой уравнением движения воды в горизонтальной трубке:
где ρ – плотность воды. Давление в точке С больше давления в точке В, поэтому вода будет выливаться из правой вертикальной трубки. Из условия неразрывности струи жидкость при этом будет отсасываться из левой вертикальной трубки. В установившемся режиме правая трубка будет полностью заполнена водой, а левая – частично. Поскольку вылилась 1/16 массы всей воды, что соответствует массе воды в части трубки длиной L/4, то в левой трубке останется столбик воды высотой 3/4L. Поэтому давления в точках В и С будут равны
где p0 – атмосферное давление.
Исключая из всех уравнений рB и рС, получим систему двух уравнений относительно рА и а:
Решая эту систему относительно рА, найдем
Задача 5. Тонкая, запаянная с одного конца и изогнутая под прямым углом трубка заполнена ртутью и закреплена на горизонтальной платформе, которая вращается с угловой скоростью ω вокруг вертикальной оси (рис. 4). При вращении платформы ртуть не выливается и полностью заполняет горизонтальное колено. Открытое колено трубки вертикально. Геометрические размеры установки указаны на рисунке; атмосферное давление р0; плотность ртути ρ. Найдите давление ртути у запаянного конца трубки.
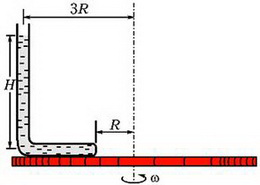
Рис. 4.
Выделим в горизонтальной части трубки небольшой элемент ртути длиной dr, расположенный на произвольном расстоянии r от оси вращения (рис. 5).
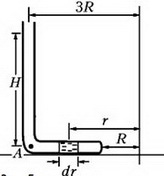
Рис. 5.
Этот элемент вращается в горизонтальной плоскости с угловой скоростью ω. Запишем уравнение движения выделенного элемента:
где S – площадь поперечного сечения трубки, dp – разность давлений между левым концом элемента ртути и правым. После сокращения на S получим связь между малыми приращениями dp и dr:
Проинтегрируем обе части этого уравнения и получим
Константу определим из условия, что при r = 3R (точка А) давление равно
и получим зависимость p(r)
Отсюда найдем давление ртути у запаянного конца трубки (r = R):
Задача 6. Стеклянный шар объемом V и плотностью ρ находится в сосуде с водой (рис. 6). Угол между стенкой сосуда и горизонтальным дном α, внутренняя поверхность сосуда гладкая, плотность воды ρ0. Найдите силу давления шара на дно сосуда в двух случаях: 1) сосуд неподвижен; 2) сосуд движется с постоянным горизонтальным ускорением а.
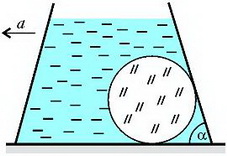
Рис. 6.
Сначала рассмотрим движущийся по горизонтали с постоянным ускорением а сосуд с водой. Введем систему координат XY, связанную с сосудом, как это изображено на рисунке 7.
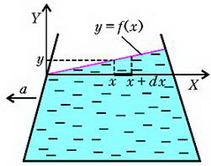
Рис. 7.
Наша задача – найти уравнение свободной поверхности жидкости в сосуде, который движется с горизонтальным ускорением а. Для этого выделим маленький элемент жидкости на оси Х, длина которого dx, а площадь поперечного сечения равна единице. С левого торца этого элемента давление равно
а с правого торца оно равно
где у – высота столба жидкости в точке х, а – аналогичная высота в точке . Так как наш элемент жидкости движется с ускорением а, его уравнение движения имеет вид
Отсюда получаем
или в интегральном виде —
Поскольку при х = 0 у = 0, константа тоже равна нулю, а уравнение свободной поверхности жидкости выглядит так:
Линии, параллельные свободной поверхности, внутри жидкости являются линиями постоянного давления. Таким образом, жидкость, движущаяся с горизонтальным ускорением а, эквивалентна неподвижной жидкости, находящейся в новом поле тяжести с эффективным «ускорением свободного падения», равным и направленным под углом к вертикали (рис. 8). Вертикальная составляющая этого эффективного ускорения равна обычному ускорению свободного падения g, а горизонтальная составляющая численно равна ускорению сосуда и направлена в противоположную сторону.
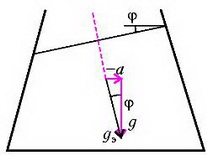
Рис. 8.
В том случае, когда сосуд неподвижен (а = 0), эффективное ускорение равно g и направлено по вертикали. Силы, действующие на стеклянный шар в этом случае, показаны на рисунке 9.
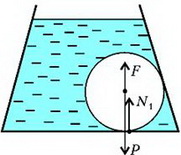
Рис. 9.
Здесь – вес (точнее – сила тяжести) шара, – выталкивающая сила, а N1 – сила реакции дна сосуда на шар. Из условия равновесия шара найдем, что
Очевидно, что сила давления шара на дно численно равна силе реакции дна и направлена в противоположную сторону.
В случае движущейся с горизонтальным ускорением a жидкости или неподвижной жидкости, но находящейся в поле с новым «ускорением свободного падения» gЭ, на шар будут действовать следующие силы (рис.10): вертикальная составляющая нового веса шара , горизонтальная составляющая этого веса , вертикальная составляющая выталкивающей силы , ее горизонтальная составляющая , реакция опоры Т со стороны боковой стенки и, наконец, сила N2 – сила реакции на шар со стороны дна сосуда. Запишем условие равновесия шара, т.е. равенство нулю всех сил, действующих на шар по вертикали:
и по горизонтали:
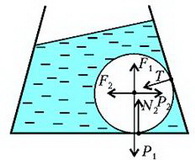
Рис. 10.
Исключая из этих уравнений Т, найдем искомую силу N2:
Разумеется, и в этом случае сила давления шара на дно сосуда численно равна силе реакции дна, но направлена в противоположную сторону.
Упр
