В сосуде содержащий воду массой 100 кг при температуре 10

Задачи на количество теплоты с решениями
Формулы, используемые на уроках «Задачи на количество теплоты,
удельную теплоемкость».
1 г = 0,001 кг; 1 т = 1000 кг; 1 кДж = 1000 Дж; 1 МДж = 1000000 Дж
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?
При решении задачи нужно учесть, что оба тела — и котёл, и вода — будут нагреваться вместе. Между ними происходит теплообмен. Их температуры можно считать одинаковыми, т. е. температура котла и воды изменяется на 100 °С — 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми. Ведь их массы и удельные теплоёмкости различны.

Задача № 2.
Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.

Задача № 3.
Стальная деталь массой 3 кг нагрелась от 25 до 45 °С. Какое количество теплоты было израсходовано?

Задача № 4.
В сосуде содержится 3 л воды при температуре 20 °С. Сколько воды при температуре 45 °С надо добавить в сосуд, чтобы в нём установилась температура 30 °С? Необходимый свободный объём в сосуде имеется. Теплообменом с окружающей средой пренебречь

Задача № 5.
На сколько градусов изменилась температура чугунной детали массой 12 кг, если при остывании она отдала 648000 Дж теплоты?

Задача № 6.
По графику определите удельную теплоёмкость образца, если его масса 50 г.
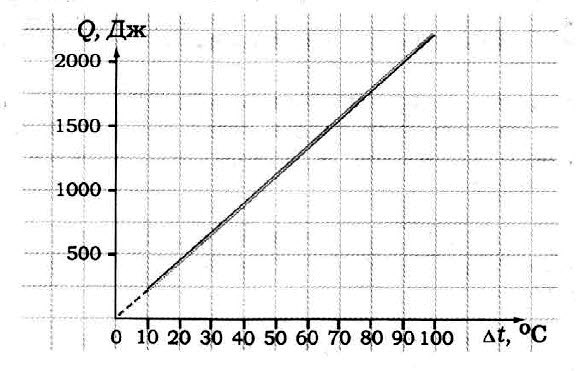

Задача № 7.
Для нагревания медного бруска массой 3 кг от 20 до 30 °С потребовалось 12000 Дж теплоты. Какова удельная теплоемкость меди?

Задача № 8.
Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей 2,1 кДж энергии. Чему равна удельная теплоемкость камня?
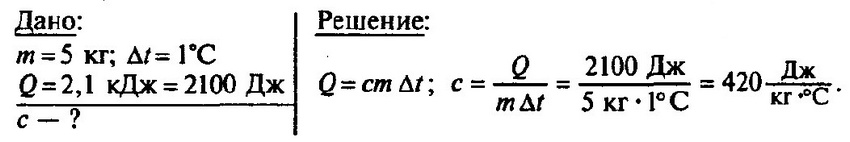
Задача № 9.
Какое количество теплоты потребуется для нагревания на 1 °С воды объемом 0,5 л; олова массой 500 г; серебра объемом 2 см3; стали объемом 0,5 м3; латуни массой 0,2 т?

Задача № 10.
Какое количество теплоты получили алюминиевая кастрюля массой 200 г и находящаяся в ней вода объемом 1,5 л при нагревании от 20 °С до кипения при температуре 100 °С?

Задача № 11.
а) Воздух, заполняющий объем 0,5 л в цилиндре с легким поршнем, нагрели от 0 до 30 °С при постоянном атмосферном давлении. Какое количество теплоты получил воздух?
б) В порожнем закрытом металлическом баке вместимостью 60 м3 под действием солнечного излучения воздух нагрелся от 0 до 20 °С. Как и на сколько изменилась внутренняя энергия воздуха в баке? (Удельная теплоемкость воздуха при постоянном объеме равна 720 Дж/кг-°С.)

Задача № 12.
ОГЭ
Металлический цилиндр массой m = 60 г нагрели в кипятке до температуры t = 100 °С и опустили в воду, масса которой mв = 300 г, а температура tв = 24 °С. Температура воды и цилиндра стала равной Θ = 27 °С. Найти удельную теплоёмкость металла, из которого изготовлен цилиндр. Удельная теплоёмкость воды св = 4200 Дж/(кг К).

Краткая теория для решения Задачи на количество теплоты.

Конспект урока «Задачи на количество теплоты».
Посмотреть конспект урока по теме «Количество теплоты. Удельная теплоемкость»
Следующая тема: «ЗАДАЧИ на сгорание топлива с решениями».
Источник
1. На рисунке представлен график зависимости температуры t от времени τ для куска льда массой 480 г, помещённого при температуре −20 °С в калориметр. В тот же калориметр помещён нагреватель. Найдите, какую мощность развивал нагреватель при плавлении льда, считая эту мощность в течение всего процесса постоянной. Теплоёмкостью калориметра и нагревателя можно пренебречь. (Удельная теплота плавления льда — 330 кДж/кг.)
Решение.
Чтобы расплавить весь имеющийся лёд необходимо затратить энергию:
Здесь m — масса льда, λ — удельная теплота плавления льда.
Мощность нагревателя W — есть расход энергии в единицу времени. Время плавления определяем по графику:
Тогда, используя табличные данные и данные задачи, получаем:
Ответ: 330 Вт.
2. Сколько граммов воды можно нагреть на спиртовке на 30 °С, если сжечь в ней 21 грамм спирта? КПД спиртовки (с учётом потерь теплоты) равен 30 %. (Удельная теплота сгорания спирта 2,9·107Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг·°С)).
Решение.
При нагревании тела на температуру тело получает количество теплоты При сгорании тела выделяется энергия Учитывая, что КПД спиртовки равен 30 %, получаем:
Ответ: 1450 г.
3. Теплоизолированный сосуд содержит смесь льда и воды, находящуюся при температуре 0 °С. Масса льда 40 г, а масса воды 600 г. В сосуд впускают водяной пар при температуре +100 °С. Найдите массу впущенного пара, если известно, что окончательная температура, установившаяся в сосуде, равна +20 °С.
Решение.
Окончательная температура положительна, значит, весь лед расплавился, и вся получившаяся вода нагрелась.
При этом пар конденсировался и полученная вода остыла. С учетом этого запишем уравнение теплового баланса:
и выразим отсюда массу пара:
Здесь Qпол и Qотд — полученная и отданная теплота соответственно, m1, m2, m3 — массы льда, воды, пара соответственно, λ — удельная теплота плавления льда, c — удельная теплоемкость воды, τ — удельная теплота парообразования, t2 — конечная температура, t1 — исходная температура смеси лед-вода, t3 — температура пара.
Переведя граммы в килограммы и подставляя данные задачи и табличные данные, получаем:
Ответ: 25,4 г.
4. Литровую кастрюлю, полностью заполненную водой, из комнаты вынесли на мороз. Зависимость температуры воды от времени представлена на рисунке. Какое количество теплоты выделилось при кристаллизации и охлаждении льда?
Примечание.
Удельную теплоту плавления льда считать равной
Решение.
Поскольку объём воды равен одному литру, масса воды равна одному килограмму. Таким образом, кристаллизовался 1 кг льда, выделив при этом
Также тепло выделялось при охлаждении льда:
Следовательно, при кристаллизации и охлаждении льда выделилось 372 кДж энергии.
Ответ: 372 кДж.
5. Сколько граммов спирта нужно сжечь в спиртовке, чтобы нагреть на ней воду массой 580 г на 80 °С? КПД спиртовки (с учётом потерь теплоты) равен 20%. (Удельная теплота сгорания спирта 2,9·107Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг·°С)).
Решение.
При нагревании тела на температуру тело получает количество теплоты При сгорании тела выделяется энергия Учитывая, что КПД спиртовки равен 20%, получаем:
Ответ: 33,6 г.
6. Какое количество теплоты выделится при кристаллизации 2 кг расплавленного олова, взятого при температуре кристаллизации, и последующем его охлаждении до 32 °С? (Удельная теплоёмкость олова — 230 Дж/(кг · °С).)
7. Тонкостенный сосуд содержит смесь льда и воды, находящуюся при температуре 0 °С. Масса льда 350 г, а масса воды 550 г. Сосуд начинают нагревать на горелке мощностью 1,5 кВт. Сколько времени понадобится, чтобы довести содержимое сосуда до кипения? Потерями теплоты и удельной теплоёмкостью сосуда, а также испарением воды можно пренебречь.
Решение.
Чтобы довести содержимое сосуда до кипения за время τ, необходимо расплавить лёд, а затем нагреть всю получившуюся воду до температуры кипения, следовательно, затратить энергию, равную
Здесь m1, m2, — массы льда и воды соответственно, λ — удельная теплота плавления льда, c — удельная теплоёмкость воды, t2 — температура кипения воды, t1 — исходная температура смеси лед-вода.
Мощность горелки W есть расход энергии в единицу времени, откуда находим τ:
Подставляя табличные данные и данные задачи, находим:
Ответ: 5,5 мин.
8. На рисунке представлен график зависимости температуры от полученного количества теплоты для вещества массой 1 кг. Первоначально вещество находилось в твёрдом состоянии. Определите удельную теплоёмкость вещества в твёрдом состоянии.
Решение.
Удельная теплоёмкость — это количество теплоты, необходимое для того, чтобы нагреть вещество на 1 °C. Из графика видно, что для нагревания 1 кг вещества на 200 °C потребовалось 50 кДж. Таким образом, удельная теплоёмкость равна:
Ответ:
9. В тонкостенный сосуд налили воду, поставили его на электрическую плитку мощностью 800 Вт и начали нагревать. На рисунке представлен график зависимости температуры воды t от времени τ. Найдите массу налитой в сосуд воды. Потерями теплоты и теплоёмкостью сосуда пренебречь.
10. Какое количество теплоты потребуется, чтобы в алюминиевом чайнике массой 700 г вскипятить 2 кг воды? Первоначально чайник с водой имели температуру 20 °С.
Примечание.
Удельную теплоёмкость алюминия считать равной
Решение.
Для нагревания чайника необходимо
Для нагревания воды:
Всего потребуется
Ответ: 723,52 кДж.
11. Какое количество теплоты выделится при конденсации 2 кг пара, взятого при температуре кипения, и последующего охлаждения воды до 40 °С при нормальном атмосферном давлении?
Решение.
В данном случае тепло отдавали пар и получившаяся из него вода. Пар отдал:
вода отдала:
Таким образом:
Ответ: 5104 кДж.
12. Какое минимальное количество теплоты необходимо для превращения в воду 500 г льда, взятого при температуре −10 °С? Потерями энергии на нагревание окружающего воздуха пренебречь.
Решение.
Для нагревания льда до температуры плавления необходимо:
Для превращения льда в воду:
Таким образом:
Ответ: 175 500 Дж.
13. В сосуд с водой положили кусок льда. Каково отношение массы льда к массе воды, если весь лёд растаял и в сосуде установилась температура 0 °С? Теплообменом с окружающим воздухом пренебречь. Начальные температуры воды и льда определите из графика зависимости температуры t от времени τ для воды и льда в процессе теплообмена.
Решение.
Лёд растает за счёт того, что вода будет остывать и тем самым отдавать своё тепло. Запишем это в формульном виде: где — теплоёмкость воды, — удельная теплота плавления льда, — масса воды и льда соответственно.
Таким образом,
Ответ: 0,42.
14. Как изменится внутренняя энергия 500 г воды, взятой при 20°С, при её превращении в лёд при температуре 0 °С?
Решение.
При охлаждении воды до 0 °С выделится количество теплоты, равное:
Затем при кристаллизации воды выделится количество теплоты, равное:
Таким образом, всего вода отдаст теплоты.
Ответ: 207 кДж.
15. В стакан массой 100 г, долго стоявший на улице, налили 200 г воды из лужи при температуре +10 °С и опустили в неё кипятильник. Через 5 минут работы кипятильника вода в стакане закипела. Пренебрегая потерями теплоты в окружающую среду, найдите мощность кипятильника. Удельная теплоёмкость материала стакана равна 600 Дж/(кг · °С).
16. Два однородных кубика привели в тепловой контакт друг с другом (см. рисунок). Первый кубик изготовлен из цинка, длина его ребра 2 см, а начальная температура t1 = 1 °C. Второй кубик изготовлен из меди, длина его ребра 3 см, а начальная температура t2 = 74,2 °C. Пренебрегая теплообменом кубиков с окружающей средой, найдите температуру кубиков после установления теплового равновесия.
Примечание.
Плотности цинка и меди соответственно:
Удельные теплоёмкости цинка и меди соответственно:
Решение.
При нагревании(охлаждении) тела на температуру тело получает(отдаёт) количество теплоты Более горячее тело передаёт тепло более холодному, запишем уравнение теплового баланса: Заметим, что теплоёмкости цинка и меди равны, поэтому их можно сократить. Раскроем скобки:
Найдём массы кубиков:
Подставим эти значения в формулу для конечной температуры:
Ответ:
17. Сколько литров воды при 83 °С нужно добавить к 4 л воды при 20 °С, чтобы получить воду температурой 65 °С? Теплообменом с окружающей средой пренебречь.
Решение.
Плотность воды равна 1 кг/л, теплоемкость равна 4 200 Дж/кг. Таким образом, изначально мы имеем m0 = 4 кг воды при температуре t0 = 20 °C. Добавляется некоторое количество воды массой m1 при температуре t1 = 83 °C. Конечная температура смеси равна tкон, а её масса m0 + m1.
Составим уравнение теплового баланса для процесса:
— отданное в процессе тепло;
— полученное в процессе тепло;
.
Таким образом,
следовательно, необходимо 10 л воды.
Ответ: 10.
18. В тонкостенный сосуд налили воду массой 1 кг, поставили его на электрическую плитку и начали нагревать. На рисунке представлен график зависимости температуры воды t от времени τ. Найдите мощность плитки. Потерями теплоты и теплоёмкостью сосуда пренебречь.
Решение.
Мощность, это отношение теплоты ко времени, за которую эта теплота получена Теплота, полученная телом при нагревании на температуру рассчитывается по формуле Используя график, найдём мощность плитки:
Ответ: 700 Вт.
19. 3 л воды, взятой при температуре 20 °С, смешали с водой при температуре 100 °С. Температура смеси оказалась равной 40 °С. Чему равна масса горячей воды? Теплообменом с окружающей средой пренебречь.
Решение.
Более холодная вода нагрелась за счет остывания горячей воды: . Масса воды вычисляется по формуле:
Выражаем массу горячей воды:
Ответ: 1.
20. Килограммовый кусок льда внесли с мороза в тёплое помещение. Зависимость температуры льда от времени представлена на рисунке. Какое количество теплоты было получено в интервале времени от 50 мин до 60 мин?
Решение.
Исходя из графика, в интервале от 50 до 60 минут происходил нагрев воды от 0 °C до 20 °C. Вычислим количество теплоты:
Ответ: 84 кДж.
21. В стакан массой 100 г, долго стоявший на столе в комнате, налили 200 г воды при комнатной температуре +20 °С и опустили в неё кипятильник мощностью 300 Вт. Через 4 минуты работы кипятильника вода в стакане закипела. Пренебрегая потерями теплоты в окружающую среду, найдите удельную теплоёмкость материала стакана.
22. Два однородных кубика привели в тепловой контакт друг с другом. Первый кубик изготовлен из меди, длина его ребра 3 см, а начальная температура t1 = 2 °C. Второй кубик изготовлен из алюминия, длина его ребра 4 см, а начальная температура t2 = 74 °C. Пренебрегая теплообменом кубиков с окружающей средой, найдите температуру кубиков после установления теплового равновесия.
Примечание.
Плотности алюминия и меди соответственно:
Удельные теплоёмкости алюминия и меди соответственно:
Решение.
При нагревании(охлаждении) тела на температуру тело получает(отдаёт) количество теплоты Более горячее тело передаёт тепло более холодному, запишем уравнение теплового баланса: Раскроем скобки:
Найдём массы кубиков:
Подставим эти значения в формулу для конечной температуры:
Ответ:
23. Двигатель трактора совершил полезную работу 23 МДж, израсходовав при этом 2 кг бензина. Найдите КПД двигателя трактора.
Решение.
При сгорании 2 кг бензина выделяется теплоты, где — удельная теплота сгорания бензина. КПД рассчитывается по формуле:
Ответ: 25 %.
24. Автомобиль УАЗ израсходовал 30 кг бензина за 2 ч. езды. Чему равна мощность двигателя автомобиля, если его КПД составляет 30%? (Удельная теплота сгорания бензина 4,6·107Дж/кг).
Решение.
Энергия, полученная двигателем от 30 кг бензина КПД определяется как отношение полезной работы к энергии, потребляемой двигателем Мощность двигателя — это отношение полезной работы совершаемой двигателем ко времени:
Ответ: 57,5 кВт.
25. В сосуд с водой положили кусок льда. Каково отношение массы воды к массе льда, если весь лёд растаял и в сосуде установилась температура 0 °С? Теплообменом с окружающим воздухом пренебречь. Начальную температуру воды и льда определите из графика зависимости от времени для воды и льда в процессе теплообмена.
Решение.
Лед растает за счёт того, что вода будет остывать и тем самым отдавать своё тепло. Запишем это в формульном виде: где — удельная теплоёмкость воды, — удельная теплота плавления льда, — масса воды и льда соответственно.
Таким образом,
Ответ: 2,38.
Источник
Решебник по физике Л.А. Кирик Самостоятельные и контрольные работы
1. а) В стихотворении М. Ю. Лермонтова «Боярин Орша» есть
такие строки:
…Светает. В поле тишина.
Густой туман, как пелена
С посеребренною каймой,
Клубится над Днепром-рекой.
Почему над рекой образуется туман? Почему туман над рекой имеет «посеребренную кайму»?
Ночью воздух над поверхностью воды охлаждается больше, чем сама вода, и его температура оказывается ниже. Потому с тёплой водной поверхности в холодный воздух испаряется водяной пар, который в воздухе конденсируется в капельки тумана. По краям области, занимаемой туманом, плотность его меньше. Солнечные лучи проникают сквозь граничные области тумана и создают впечатление, будто туман имеет «посеребрённую кайму».
б) 3 кг льда, взятого при -20 °С, нужно нагреть до кипения и испарить. Сколько для этого потребуется теплоты? Изобразите процесс графически.
2. а) Как известно, после дождя цветы начинают пахнуть сильнее (см. рисунки). Почему?
Запах цветов зависит от испарения пахучих эфирных масел, образующихся в нектарнике цветов.
б) Сколько необходимо сжечь спирта, чтобы 2 кг льда, взятого при -5 °С, расплавить и 1 кг полученной воды превратить в пар? КПД спиртовки 40 %.
3. а) Объясните, почему в кастрюле-скороварке (см. рисунок) мясо можно сварить гораздо быстрее, чем в обычной кастрюле.
Температура кипения воды повышается, т.к. над поверхностью воды поддерживается примерно удвоенное давление.
б) Расплавленный алюминий массой 1,2 кг, взятый при температуре плавления, влили в воду, масса которой 2,1 кг и температура 16 °С. Определите, сколько воды выкипит при этом. Теплообмен с окружающей средой отсутствует.
4. а) В стихотворении Ф. И. Тютчева «Утро в горах» есть такие строки:
Лишь высших гор до половины
Туманы покрывают скат,
Как бы воздушные руины
Волшебством созданных палат.
Почему склоны высоких гор бывают в тумане?
Теплые слои воздуха поднимаются по склону горы вверх и попадают в область относительно холодного воздуха, в процессе охлаждения поднявшегося теплого воздуха, образуется туман.
б) В бак, содержащий воду массой 10 кг при температуре 20 °С, бросили кусок железа массой 2 кг, нагретый до температуры 500 °С. При этом некоторое количество воды превратилось в пар. Конечная температура, установившаяся в баке, равна 24 °С. Определите массу воды, обратившейся в пар.
5. а) О каких физических явлениях говорится в следующих пословицах:
«Горшки легко закипают через край — к ненастью»; кипение
«Что сильно кипит, быстро испаряется; что сильно бурлит, вырывается наружу»? испарение
б) В кусок льда массой 100 г и температурой -10 °С влили 1,5 кг расплавленного свинца при температуре плавления. Сколько воды обратится в пар, если свинец остыл до температуры 27 °С? Потерями энергии можно пренебречь.
6. а) В стихотворении Вадима Казаченко «Туман над рекой» есть такие строки:
Туман над рекою, над синей водою,
Туман над рекою нас прятал с тобою.
Туман над рекою опять нас зовет,
В тумане любовь нас с тобою найдет…
Объясните происхождение тумана над рекой (см. рисунок).
Образование тумана связано с холодным потоком воздуха, спускающимся на теплые поверхности воды.
б) Сколько сухих дров нужно сжечь в печи с КПД 40 %, чтобы 200 кг снега, взятого при температуре -10 °С, полностью обратить в пар.
7. В сосуде, из которого быстро откачивают воздух, находится небольшое количество воды массой т при температуре 0 °С. За счет интенсивного испарения происходит постепенное замораживание воды. Какая часть первоначальной массы воды может быть таким образом превращена в лед?
8. В алюминиевую кастрюлю массой 600 г налили 1,5 л воды с температурой 20 °С и поставили на электроплитку, КПД которой 75 %. Через 35 мин вода закипела и 20 % ее превратилось в пар. Какова мощность электроплитки?
9. Рассчитайте, с какой высоты должна упасть капля воды, чтобы при ударе о землю полностью испариться? Начальная температура капли 20 °С. Считайте, что вся потенциальная энергия капли пошла на ее нагрев и испарение.
10. В кастрюлю налили холодную воду при температуре 10 °С и поставили на электроплитку. Через 10 мин вода закипела. Через какое время она полностью испарится?
Источник
