В сосуде вместимостью 10 л находится азот массой

= (Q1 – Q2 ) / Q1 = (Т1 – Т2) / Т1,

где Т1 и Т2 – температуры нагревателя и холодильника. 20. Приращение энтропии системы:

S Q/T,

где Q – элементарное тепло, получаемое системой.

21. Связь между энтропией и термодинамической вероятностью:

S = k lnW,

где k – постоянная Больцмана, W – термодинамическая вероятность системы.

3.2. Примеры решения задач

Задача 1. В сосуде объёмом V = 5 л находится азот массой m = 1,4 г при температуре Т = 1800 К. Найти давление газа, имея в виду, что при этой температуре =30% молекул диссоциировано на атомы.

Решение

Так как часть молекул диссоциирована на атомы, то в сосуде находится смесь двух газов с молярными массами М1=28 г и М2 = М1/2 =14 г уравнения состояния обоих газов имеют вид:

где P1 и P2 – парциальные давления молекулярного (N2) и атомарного (N1) азота. Давление смеси газов подчиняется закону Дальтона:

P P1 P2.

Сложим уравнения (1) и (2):

Так как m1+m2=m (масса газа), то

Отсюда,

P mRT 1 1,9 105 Па.

VM1

Задача 2. На какой высоте давление воздуха составляет 60 % от давления на уровне моря? Считать температуру воздуха везде одинаковой и равной 10О С.

Решение

Зависимость давления от высоты имеет вид:

Mgh

На уровне моря h0=0, поэтому p e RT . p0

Прологарифмируем обе части

Задача 3. Найти среднюю продолжительность свобод-

ного пробега молекул кислорода при температуре Т = 250 К и давлении P =100 Па.

Решение

Средняя продолжительность свободного пробега

молекул – величина, обратная среднему числу столкновений, происходящих за 1 секунду:

где n – концентрация молекул кислорода.

Из уравнения состояния идеального газаn p , kT

Эффективный диаметр молекул кислорода (величина справочная) d = 0,36 нм = 3,6 10 10 м.

Задача 4. Определить отношение удельных теплоёмкостей для смеси газов, содержащей гелий массой m1=8 г и водород массой m2 = 2 г.

Решение

Для нагревания смеси газов массой m m1 m2 на T при постоянном объёме ей необходимо сообщить количество теплоты Q c m T,где cv – удельная теплоёмкость смеси.

Так как гелий – газ одноатомный, то i1=3, водород – газ

Подставляя выражение для удельных теплоёмкостей, получим:

Конечную температуру найдём из уравнения адиабаты:

Так как cp и газ двухатомный, то c

i 2 7 .

i5

A U 4030 Дж .

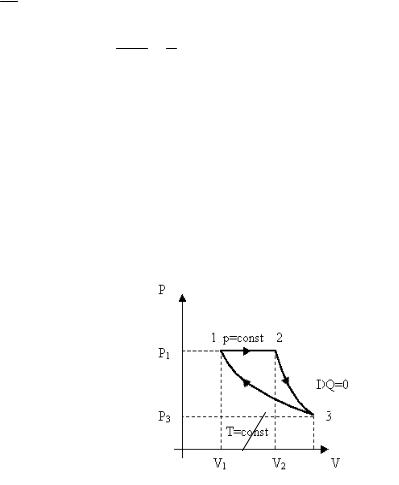
Задача 7. Вычислить К.П.Д. цикла, состоящего из изобарного, адиабатного и изотермического процессов, если в результате изобарного процесса газ нагревается от Т1=300 К до

Т2=600 К.

сжатия газ отдаёт количество теплоты Q31 холодильнику. К.п.д. любого цикла определяется выражением

Q12 Q31 ,

Q12

Q31 v RT1 i 2ln T2 ;

2 T1

Задача 8. Найти изменение энтропии при следующих процессах:

а) при нагревании 100 г воды от 0О С до 100О С и последующем превращении воды в пар той же температуры; б) при изотермическом расширении 10 г кислорода от объёма 25 л до объёма 100 л.

Решение

а) Полное изменение энтропии S равно сумме изменения энтропии при нагревании воды S1 и изменения энтропии при превращении воды в пар S2:

S S1 S2.

Пользуясь определением изменения энтропии, найдём:

гдеQ rm – количество теплоты, переданное при превращении нагретой воды в пар той же температуры, r – удельная теплота парообразования.

rm

S2 T2 .

Тогда

постоянной, поэтому 1 можно вынести за знак интеграла:

Т

Согласно I начала термодинамики

3.3.Задачи для выполнения контрольной работы №2

3.01.В баллоне вместимостью V=3 л содержится кислород массой m=10 г. Определить концентрацию n молекул газа.

3.02.Определить количество вещества водорода, заполняющего сосуд объемом V = 3 л, если концентрация молекул газа

всосуде n = 2∙10 18 м-3.

3.03.Определить концентрацию n молекул кислорода,

находящегося в сосуде объемом V = 2 л. Количество вещества ν кислорода равно 0,2 моль.

3.04. Вода при температуре t=4оС занимает объем V=1см3. Определить количество вещества ν и число N молекул воды.

3.05. Определить количество вещества ν и число N молекул азота массой m = 0,2 кг.

3.06. Определить число атомов в 1 кг водорода и массу одного атома водорода.

3.07. Вычислить плотность ρ азота, находящегося в баллоне под давлением Р = 2 МПа и имеющего температуру Т

= 400 К.

3.08. Определить плотность ρ водяного пара, находящегося под давлением Р = 2,5 кПа и имеющего температуру Т

=250 К.

3.09.В баллоне находится газ при температуре Т1= 400К. До какой температуры Т2 надо нагреть газ, чтобы его давление увеличилось в 1,5 раза?

3.10.Какому давлению необходимо подвергнуть углекислый газ при температуре Т = 300К, чтобы его плотность

оказалась равной = 500 г/л?

3.11.Плотность смеси азота и водорода при температуре t

=47 С и давлении P = 2.105 Па равна = 0,3 г л. Найти

концентрации молекул азота (n1) и водорода ( n2) в смеси. 3.12. В баллоне емкостью 2 м3 содержится смесь азота N2 и

окиси азота NO. Определить массу окиси азота, если масса смеси равна 14г, температура 300К и давление 0,6 106 Па.

3.13.Найти плотность газовой смеси, состоящей по массе из одной части водорода и восьми частей кислорода при давлении Р = 100 кПа и температуре Т = 300 К.

3.14.В баллоне, объём которого 0,25 м3, находится газ, состоящий из смеси СО2 и паров воды. Температура газа

327 С. Число молекул углекислого газа N1 = 6,6.1021. Найти давление и молярную массу газовой смеси.

3.15. Определить давление и молекулярную массу смеси газов, состоящей из 10г кислорода и 10г азота, которые занимают объём 20 л при температуре 150 С.

3.16. Определите плотность смеси газов водорода массой m1 =8 г и кислорода массой m2 =64 г при температуре Т = 290 К и давлении 0,1 МПа.