В сосуде закрытом поршнем находится в равновесии
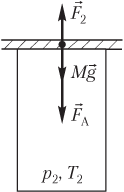
11. МКТ и Термодинамика (объяснение явлений)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
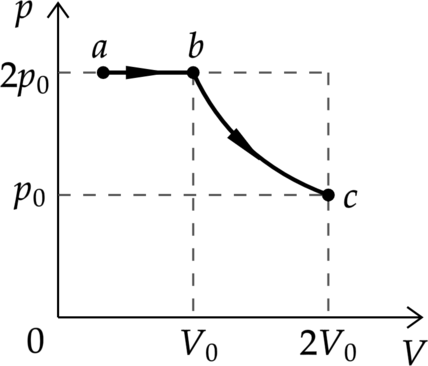
В цилиндрическом сосуде, закрытом подвижным поршнем, находится водяной пар и капля воды. С паром в сосуде при постоянной температуре провели процесс (a rightarrow b rightarrow c), (pV) –диаграмма которого представлена на рисунке. Из приведённого ниже списка выберите два правильных утверждения относительно проведённого процесса. 1) На участке (brightarrow c) масса пара уменьшается. 2) На участке (a rightarrow b) к веществу в сосуде подводится положительное количество теплоты. 3) В точке (c) водяной пар является насыщенным. 4) На участке (a rightarrow b) внутренняя энергия капли уменьшается. 5) На участке (b rightarrow c) внутренняя энергия пара уменьшается.
“Демоверсия 2021”
1) Пар в точке (b) перестает быть насыщенным (до этого происходило испарение) и масса пара перестает изменяться
Утверждение 1 – (color{red}{small text{Неверно}})
2) При переходе из жидкого в газообразное состояние внутренняя энергия вещества увеличивается, следовательно, первый закон термодинамики запишется в виде [Q=Delta U(>0)pDelta V] Объем увеличивается, значит подводится положительное количество теплоты
Утверждение 2 – (color{green}{small text{Верно}})
3) Из пункта 1) утверждение неверно
Утверждение 3 – (color{red}{small text{Неверно}})
4) Масса капель уменьшается, следовательно, их внутренняя энергия тоже уменьшается
Утверждение 4 – (color{green}{small text{Верно}})
5) Масса пара и температура постоянны, следовательно и внутренняя энергия постоянна Утверждение 5 – (color{red}{small text{Неверно}})
Ответ:
В стеклянную колбу налили немного воды и герметично закрыли её пробкой. Вода постепенно испарялась. На рисунке показан график изменения со временем t концентрации n молекул водяного пара внутри колбы. Температура в колбе в течение всего времени проведения опыта оставалась постоянной. В конце опыта в колбе ещё оставалась вода. Из приведённого ниже списка выберите два правильных утверждения относительно описанного процесса.
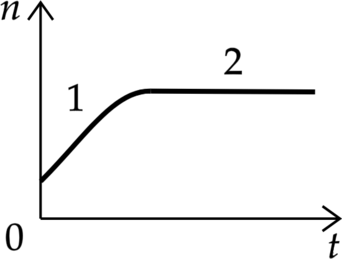
1) На участке 1 водяной пар ненасыщенный, а на участке 2 насыщенный.
2) На участке 2 давление водяных паров не менялось.
3) На участке 1 плотность водяных паров уменьшалась.
4) На участке 2 плотность водяных паров увеличивалась.
5) На участке 1 давление водяных паров уменьшалось
“Досрочная волна 2020 вариант 1”
1) (color{green}{small text{Верно}})
На участке 1 давление пара меняется, а на участке 2 – уже нет, следовательно, на участке 1 пар ненасыщенный, а на участке 2 – насыщенный
2) (color{green}{small text{Верно}})
Как известно из первого пункта, на участке 2 пар насыщенный, значит, его давление не изменяется.
3 ) (color{red}{small text{Неверно}})
Плотность водяных паров изменяется пропорционально концентрации, следовательно, при увеличении концентрации плотность водяных паров также увеличивается.
4) (color{red}{small text{Неверно}})
Как известно из первого пункта, пар на участке 2 — насыщенный, следовательно, его плотность на участке 2 не изменяется.
5) (color{red}{small text{Неверно}})
Давление водяных паров изменяется пропорционально концентрации, следовательно, при увеличении концентрации давление водяных паров также увеличивается
Ответ: 12
В закрытом сосуде измерили относительную влажность воздуха, которая была равна 30%. После объем увеличили в 3 раза, не изменяя температуру. Выберите два верных утверждения, описывающих этот процесс.
1) В ходе процесса относительная влажность воздуха уменьшилась до 10%.
2) В ходе процесса выделилась роса.
3) Относительная влажность возросла до 90%.
4) Концентрация воды в воздухе уменьшилась.
5) Концентрация воды в воздухе увеличилась.
1) (color{green}{small text{Верно}})
Относительная влажность воздуха рассчитывается: [varphi=dfrac{p_text{в.п.}}{p_text{нас}}cdot100%] Из уравнения Менделеева-Клапейрона мы знаем, что давление и объем имеют обратную зависимость. Так как объем возрастает, значит, давление падает, вслед за которым уменьшается и относительная влажность.
2) (color{red}{small text{Неверно}})
Точка росы — это температура, до которой должен охладиться воздух, чтобы содержащийся в нём пар достиг состояния насыщения и начал конденсироваться в росу. В нашем же случае температура была неизменной.
3) (color{red}{small text{Неверно}})
Смотрите пункт 1.
4) (color{green}{small text{Верно}})
Концентрацию можем высчитать по формуле: [n=dfrac{N}{V}] Количество молекул воды неизменно, а объем возрастает, выходит, концентрация уменьшилась.
5) (color{red}{small text{Неверно}})
Смотрите пункт 4.
Ответ: 14
В цилиндрический сосуд, герметично закрытый подвижным поршнем, впрыснули некоторое количество воды, после чего сдвинули поршень и дождались установления в сосуде теплового равновесия. Выберите два верных утверждения, описывающих этот процесс.
1) Если относительная влажность воздуха равна 45% при температуре 100(^circ), то масса (на литр) водяных паров равна 260 мг.
2) Если объем уменьшить, а давление не изменится, то концентрация водяных паров так же не изменится.
3) Если при начальной относительной влажности 40% уменьшить объем в 4 раза, то влажность станет 120%.
4) Если при начальной относительной влажности 40% уменьшить объем в 4 раза, то влажность станет 10%.
5) Если давление водяных паров при температуре 100(^circ) равно 56 кПа, то абсолютная влажность равна 0,33 кг/м(^3).
1) (color{green}{small text{Верно}})
Воспользуемся уравнением Менделеева-Клапейрона: [pV=dfrac{m}{mu}RT] Для того, чтобы узнать давление, распишем относительную влажность: [varphi=dfrac{p}{p_text{нас}}] [p=p_text{нас}varphi] Подставим давление в уравнение: [m=dfrac{p_text{нас}varphi Vmu}{RT}=dfrac{100 cdot 10^3 text{ Па}cdot 0,45cdot 10^{-3} text{ м}^3 cdot 18 cdot 10^{-3} text{ кг/моль}}{8,31 dfrac{text{Дж}}{text{моль}cdottext{К}}cdot (273+100)text{ К}}=260text{ мг}]
2) (color{red}{small text{Неверно}})
Если давление не изменится, значит изначально влажность была 100%, в таком случае дальше пар будет только конденсироваться.
3) (color{red}{small text{Неверно}})
Если объем уменьшается в 4 раза, то и влажность увеличивается в 4 раза, но так как она не может быть больше 100%, то пар просто становится насыщенным.
4) (color{red}{small text{Неверно}})
Смотрите пункт 3
5) (color{green}{small text{Верно}})
Абсолютная влажность воздуха – это плотность водяного пара в воздухе, который мы можем высчитать по уравнению Менделеева-Клапейрона: [pV=dfrac{m}{mu}RT] [p=dfrac{rho}{mu}RT] [rho=dfrac{pmu}{RT}=dfrac{56cdot 10^3text{ Па} cdot 18 cdot 10^{-3} text{ кг/моль}}{8,31 dfrac{text{Дж}}{text{моль}cdottext{К}}cdot (273+100)text{ К}}=0,33text{ кг/м}^3]
Ответ: 15
В комнатах (A) и (B) измерили давление водяного пара. Выберите два верных утверждения, соответствующих данной ситуации. 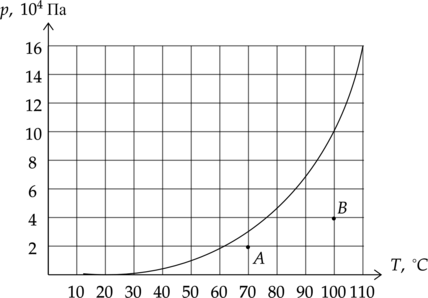
1) Если в каждой комнате понизить температуру на 10 (^circ)C , то в комнате (B) относительная влажность будет больше.
2) Абсолютная влажность в комнате (A) равна 0,6 кг/м(^3).
3) Относительная влажность в комнате (A) больше, чем в комнате (B).
4) Для выделения росы в комнате (B) нужно понизить давление на 40 кПа.
5) Для выделения росы в комнате (A) нужно понизить температуру на 10 (^circ)C.
1) (color{red}{small text{Неверно}})
По диаграмме мы видим, что в таком случае в комнате (A) пар станет насыщенным, а в комнате (B) до данного значения не дойдет.
2) (color{red}{small text{Неверно}})
Абсолютная влажность воздуха – это плотность водяного пара в воздухе, который мы можем высчитать по уравнению Менделеева-Клапейрона: [pV=dfrac{m}{mu}RT] [p=dfrac{rho}{mu}RT] [rho=dfrac{pmu}{RT}=dfrac{20cdot 10^3text{ Па} cdot 18 cdot 10^{-3} text{ кг/моль}}{8,31 dfrac{text{Дж}}{text{моль}cdottext{К}}cdot (273+70)text{ К}}=0,13text{ кг/м}^3]
3) (color{green}{small text{Верно}})
Относительная влажность: [varphi_A=dfrac{2cdot 10^4text{ Па}}{3 cdot 10^4text{ Па}}cdot 100%=67%] [varphi_B=dfrac{4 cdot 10^4text{ Па}}{10 cdot 10^4text{ Па}}cdot 100%=40%]
4) (color{red}{small text{Неверно}})
Чтобы роса начала выделяться, давление должно быть как минимум равно давлению насыщенного пара. Если мы понизим давление, ничего не случится.
5) (color{green}{small text{Верно}})
Точка росы — это температура, до которой должен охладиться воздух, чтобы содержащийся в нём пар достиг состояния насыщения и начал конденсироваться в росу. Анализируя диаграмму, мы можем заключить, что нужно понизить температуру как минимум на 10 (^circ)C, чтобы начала выделяться роса.
Ответ: 35
В цилиндрический сосуд, герметично закрытый подвижным поршнем, впрыснули некоторое количество воды, после чего сдвинули поршень и дождались установления в сосуде теплового равновесия. Выберите два верных утверждения, описывающих этот процесс.
1) Если в этот же сосуд добавить некоторое количество гелия, то относительная влажность увеличится.
2) Если давление водяных паров при температуре 95(^circ) равно 71 кПа, то абсолютная влажность равна 0,42 кг/м(^3).
3) Если при температуре 100(^circ) и давлении 50 кПа уменьшить в 4 раза объем, то масса водяного пара уменьшится в 2 раза.
4) Если относительная влажность воздуха равна 84% при температуре 100(^circ), то масса (на литр) водяных паров равна 182 мг.
5) Если уменьшить объем в 5 раз, а давление увеличится в 4, то в начальный момент времени относительная влажность была равна 20%.
1) (color{red}{small text{Неверно}})
Относительная влажность зависит только от давления насыщенного пара и паров воды в воздухе, от других газов она не зависит.
2) (color{green}{small text{Верно}})
Абсолютная влажность воздуха – это плотность водяного пара в воздухе, который мы можем высчитать по уравнению Менделеева-Клапейрона: [pV=dfrac{m}{mu}RT] [p=dfrac{rho}{mu}RT] [rho=dfrac{pmu}{RT}=dfrac{71cdot 10^3text{ Па} cdot 18 cdot 10^{-3} text{ кг/моль}}{8,31 dfrac{text{Дж}}{text{моль}cdottext{К}}cdot (273+95)text{ К}}=0,42text{ кг/м}^3]
3) (color{green}{small text{Верно}})
Так как объем уменьшился в 4 раза, а макисмальное давление насыщенного пара равно 100 кПа, то давление может увеличитсья только в 2 раза. Запишем уравнение Менделеева-Клапейрона: [pV=dfrac{m}{mu}RT] Из уравнения видно, что давление и масса имеют прямую зависимость, тогда если давление не можем уменьшить в 2 раза, уменьшится в это же количество раз масса.
4) (color{red}{small text{Неверно}})
Воспользуемся уравнением Менделеева-Клапейрона: [pV=dfrac{m}{mu}RT] Для того, чтобы узнать давление, распишем относительную влажность: [varphi=dfrac{p}{p_text{нас}}] [p=p_text{нас}varphi] Подставим давление в уравнение: [m=dfrac{p_text{нас}varphi Vmu}{RT}=dfrac{100 cdot 10^3 text{ Па}cdot 0,84cdot 10^{-3} text{ м}^3 cdot 18 cdot 10^{-3} text{ кг/моль}}{8,31 dfrac{text{Дж}}{text{моль}cdottext{К}}cdot (273+100)text{ К}}=488text{ мг}]
5) (color{red}{small text{Неверно}})
Если давление увеличилось только в 4 раза, значит, оно достигло значение давления насыщенного пара. Тогда в начальный момент времени влажность была равна: (dfrac{100}{4}=25%).
Ответ: 23
В комнатах (A) и (B) измерили давление водяного пара. Выберите два верных утверждения, соответствующих данной ситуации. 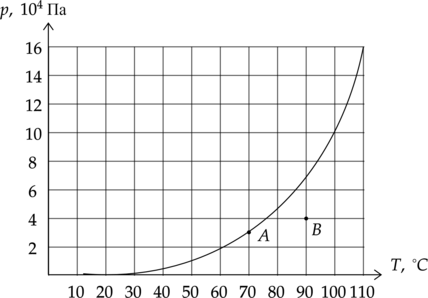
1) В комнате (B) наблюдается конденсация пара.
2) В комнате (A) относительная влажность больше, чем в комнате (B).
3) В комнате (B) абсолютная влажность пара равна 0,54 кг/м(^3).
4) Для выделения росы в комнате (B) нужно понизить температуру на 15 (^circ)C.
5) Чтобы в комнате (A) сконденсировалась половина водяного пара, нужно повысить давление в 3 раза.
1) (color{red}{small text{Неверно}})
В комнате (B) не насыщенный пар, тогда конденсация наблюдаться не может.
2) (color{green}{small text{Верно}})
В комнате (A) относительная влажность равна 100%, что можно видеть на графике. В комнате (B) же влажность меньше.
3) (color{red}{small text{Неверно}})
Абсолютная влажность воздуха – это плотность водяного пара в воздухе, который мы можем высчитать по уравнению Менделеева-Клапейрона: [pV=dfrac{m}{mu}RT] [p=dfrac{rho}{mu}RT] [rho=dfrac{pmu}{RT}=dfrac{4cdot 10^4text{ Па} cdot 18 cdot 10^{-3} text{ кг/моль}}{8,31 dfrac{text{Дж}}{text{моль}cdottext{К}}cdot (273+90)text{ К}}=0,24text{ кг/м}^3]
4) (color{green}{small text{Верно}})
Точка росы — это температура, до которой должен охладиться воздух, чтобы содержащийся в нём пар достиг состояния насыщения и начал конденсироваться в росу. По графику действительно видно, что для выделения росы нужно понизить температуру на 15 (^circ)C.
5) (color{red}{small text{Неверно}})
Запишем уравнение Менделеева-Клапейрона: [pV=dfrac{m}{mu}RT] Из уравнения видно, что давление и масса имеют прямую зависимость, тогда если объем уменьшить в 2 раза, уменьшится в это же количество раз масса.
Ответ: 24
Источник
5.4. Практическое применение уравнения состояния идеального газа
5.4.3. Уравнение состояния для газа, находящегося в сосуде под поршнем
Для идеального газа, находящегося в сосуде под поршнем, необходимо учитывать следующее:
- масса газа, находящегося в сосуде под поршнем, вследствие изменения термодинамических параметров газа не изменяется:
m = const;
- постоянным остается также количество вещества (газа):
ν = const;
- плотность газа и концентрация его молекул (атомов) изменяются:
ρ ≠ const, n ≠ const.
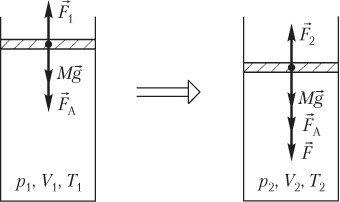
Пусть изменение состояния идеального газа, находящегося в цилиндрическом сосуде под поршнем, вызвано действием на поршень внешней силы F→ (рис. 5.9).
Рис. 5.9
Начальное и конечное состояния газа в сосуде под поршнем описываются следующими уравнениями:
p1V1=νRT1,p2V2=νRT2,}
где p
1, V
1, T
1 — давление, объем и температура газа в начальном состоянии; p
2, V
2, T
2 — давление, объем и температура газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).
Условия равновесия поршня, закрывающего идеальный газ в сосуде (см. рис. 5.9), в начале процесса и в конце процесса выглядят следующим образом:
Mg+FA=F1,Mg+FA+F=F2,}
где M — масса поршня; g — модуль ускорения свободного падения; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление; S — площадь сечения поршня; F
1 — модуль силы давления газа на поршень в начале процесса, F
1 = p
1S; p
1 — давление газа в сосуде в начальном состоянии; F — модуль силы, вызывающей сжатие газа; F
2 — модуль силы давления газа на поршень в конце процесса, F
2 = p
2S; p
2 — давление газа в сосуде в конечном состоянии.
Температура идеального газа, находящегося в сосуде под поршнем, может как изменяться, так и оставаться неизменной:
- если процесс движения поршня происходит достаточно быстро, то температура газа изменяется —
T ≠ const;
- если процесс происходит медленно, то температура газа остается постоянной –
T = const.
Давление идеального газа, находящегося в сосуде под поршнем, также может изменяться или оставаться неизменным:
- если в задаче сказано, что поршень является легкоподвижным, то давление газа под поршнем — неизменно (в том случае, когда из условия задачи не следует обратное) — p = const;
- в остальных случаях давление газа под поршнем изменяется — p ≠ const.
Масса поршня, закрывающего газ в сосуде, либо равна нулю, либо имеет отличное от нуля значение:
- если в задаче сказано, что поршень является легким или невесомым, то масса поршня считается равной нулю —
M = 0;
- в остальных случаях поршень обладает определенной ненулевой массой —
M ≠ const.
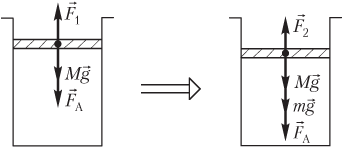
Пример 19. В вертикальном цилиндре под легкоподвижным поршнем сечением 250 мм2 и массой 1,80 кг находится 360 см3 газа. Атмосферное давление равно 100 кПа. На поршень поставили гири, и он сжал газ до объема 240 см3. Температура газа при его сжатии не изменяется. Определить массу гирь.
Решение. На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня Mg→;
- сила атмосферного давления F→A;
- сила давления газа F→1, действующая со стороны газа (до его сжатия);
- сила давления газа F→2, действующая со стороны газа (после его сжатия);
- mg→ — вес гирь.
Условие равновесия поршня запишем в следующем виде:
- до сжатия газа —
F
1 = Mg + F
A,
где F
1 — модуль силы давления газа, F
1 = p
1S; p
1 — давление газа до сжатия; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление; g — модуль ускорения свободного падения;
- после сжатия газа —
F
2 = Mg + F
A
+ mg,
где F
2 — модуль силы давления газа, F
2 = p
2S; p
2 — давление газа после сжатия; mg — вес гирь; m — масса гирь.
Считая процесс сжатия газа изотермическим, запишем уравнение Менделеева — Клапейрона для газа под поршнем следующим образом:
- до его сжатия —
p
1V
1 = νRT,
где V
1 — первоначальный объем газа под поршнем; ν — количество газа под поршнем; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа (не изменяется в ходе процесса);
- после его сжатия —
p
2V
2 = νRT,
где V
2 — объем сжатого поршнем газа.
Равенство
p
1V
1 = p
2V
2
и два условия равновесия, записанные в явном виде, образуют полную систему уравнений:
p1S=Mg+pAS,p2S=Mg+pAS+mg,p1V1=p2V2,}
которую требуется решить относительно массы гирь m.
Для этого выразим отношение давлений p
2/p
1 из первой пары уравнений:
p2p1=Mg+pAS+mgMg+pAS
и из третьего уравнения:
p2p1=V1V2,
запишем равенство правых частей полученных отношений:
Mg+pAS+mgMg+pAS=V1V2.
Отсюда следует, что искомая масса определяется формулой
m=(M+pASg)(V1V2−1).
Вычисление дает результат:
m=(1,80+100⋅103⋅250⋅10−610)(360⋅10−6240⋅10−6−1)=2,15 кг.
Указанное сжатие газа вызвано гирями массой 2,15 кг.
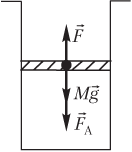
Пример 20. Открытый цилиндрический сосуд сечением 10 см2 плотно прикрывают пластиной массой 1,2 кг. Атмосферное давление составляет 100 кПа, а температура окружающего воздуха равна 300 К. На сколько градусов нужно нагреть воздух в сосуде, чтобы он приподнял пластину?
Решение. На рисунке показаны силы, действующие на пластину после нагревания газа:
- сила тяжести пластины Mg→;
- сила атмосферного давления F→A;
- сила давления газа F→2, действующая на пластину со стороны нагретого газа.
Пластина находится в состоянии неустойчивого равновесия; условие равновесия пластины выглядит следующим образом:
F
2 = Mg + F
A,
где F
2 — модуль силы давления нагретого газа, F
2 = p
2S; p
2 — давление нагретого газа; S — площадь сечения сосуда; Mg — модуль силы тяжести пластины; M — масса пластины; g — модуль ускорения свободного падения; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление.
Запишем уравнение Менделеева — Клапейрона следующим образом:
- для газа в сосуде до его нагревания
p
1V = νRT
1,
где p
1 — давление газа в сосуде до нагревания (совпадает с атмосферным давлением), p
1 = p
A; V — объем газа в сосуде; ν — количество вещества (газа) в сосуде; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T
1 — температура газа в сосуде до нагревания (совпадает с температурой окружающей среды);
- для газа в сосуде после его нагревания
p
2V = νRT
2,
где p
2 — давление нагретого газа; T
2 — температура нагретого газа.
Два уравнения состояния газа (до и после нагревания) и условие равновесия пластины, записанные в явном виде, образуют полную систему уравнений:
pAV=νRT1,p2V=νRT2,p2S=Mg+pAS;}
систему необходимо решить относительно температуры T
2, до которой следует нагреть газ.
Для этого делением первой пары уравнений
pAVp2V=νRT1νRT2
получим выражение для давления нагретого газа:
p2=pAT2T1
и подставим его в третье уравнение системы:
pAT2ST1=Mg+pAS.
Преобразуем полученное выражение к виду
T2=T1(Mg+pAS)pAS=T1(MgpAS+1),
а затем найдем разность
ΔT=T2−T1=MgT1pAS.
Произведем вычисление:
ΔT=1,2⋅10⋅300100⋅103⋅10⋅10−4=36 К=36 °С.
Пример 21. В цилиндрическом сосуде поршень массой 75,0 кг и площадью сечения 50,0 см2 начинает двигаться вверх. Давление газа под поршнем постоянно и равно 450 кПа, атмосферное давление составляет 100 кПа. Считая, что поршень движется без трения, определить модуль скорости поршня после прохождения им 3,75 м пути.
Решение. На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня Mg→;
- сила атмосферного давления F→A;
- сила давления газа F→, действующая на поршень со стороны нагретого газа.
Под действием указанных сил, направленных вверх, поршень движется с ускорением a→:
F→+F→A+Mg→=ma→,
или в проекции на вертикальную ось —
F − F
A − Mg = Ma,
где F — модуль силы давления газа под поршнем, F = pS; p — давление газа; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; g — модуль ускорения свободного падения; a — модуль ускорения поршня.
Преобразуем записанное уравнение, выразив модуль ускорения и выполнив подстановку выражений для модулей сил:
a=F−FA−MgM=(p−pA)SM−g.
Скорость поршня, его ускорение и пройденный путь связаны между собой соотношением
l=v22a,
где l — пройденный путь; v — модуль скорости поршня.
Выразим отсюда модуль скорости поршня:
v=2al
и подставим в записанную формулу выражение для модуля ускорения:
v=2l((p−pA)SM−g).
Выполним расчет:
v=2⋅3,75((450−100)⋅103⋅50⋅10−475,0−10)≈10 м/с.
После прохождения 3,75 м пути поршень приобретет скорость, приблизительно равную 10 м/с.
Источник