В сосуде заполненном гелием

8748. Объем сосуда с идеальным газом уменьшили вдвое, выпустив половину газа и поддерживая температуру газа в сосуде постоянной. Как изменятся в результате этого давление газа в сосуде и его внутренняя энергия?
Для каждой величины определите соответствующий характер изменения:
1) не изменится
2) уменьшится
3) увеличится


P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8748.
8780. В цилиндрическом сосуде под поршнем находится газ. Поршень не закреплен и может перемещаться в сосуде без трения (см. рисунок). В сосуд закачивается еще такое же количество газа при неизменной температуре. Как изменится в результате этого давление газа и концентрация его молекул?

Для каждой величины определите соответствующий характер изменения:
1) не изменится
2) уменьшится
3) увеличится


P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8780.
8812. Аргон помещают в открытый сверху сосуд под легкий подвижный поршень и начинают охлаждать, Давление воздуха, окружающего сосуд, равно 105 Па. Начальный объем газа 9 л, начальная температура 450 К. Масса газа в сосуде остается неизменной. Трением между поршнем и стенками сосуда пренебречь.
Установите соответствие между физическими величинами, характеризующими аргон, и формулами, выражающими их зависимость от абсолютной температуры Т газа в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) внутренняя энергия газа ( U(T) )
Б) объем газа ( V(T) )
ФОРМУЛЫ
1) ( dT, d = ) 3 Дж/К
2) ( frac{b}{T}, b = ) 4050 м3 ⋅ K
3) ( at, a = ) 2 ⋅ 10-5 м3/K
4) ( cT, c = ) 20 Дж/К

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8812.
8844. На рисунке показан процесс изменения состояния одного моля одноатомного идеального газа (U – внутренняя энергия газа; p – его давление). Как изменятся в ходе этого процесса объем и теплоемкость газа? Для каждой величины определите соответствующий характер изменения:

1) не изменится
2) уменьшится
3) увеличится


P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8844.
8876. В цилиндре под поршнем находится твердое вещество. Цилиндр поместили в раскаленную печь. На рисунке показан график изменения температуры T вещества по мере поглощения им количества теплоты Q. Какие участки графика соответствуют нагреванию вещества в газообразном состоянии и кипению жидкости?

ТЕПЛОВЫЕ ПРОЦЕССЫ
А) кипение жидкости
Б) нагревание вещества в газообразном состоянии
УЧАСТКИ ГРАФИКА
1) 1
2) 2
3) 3
4) 4

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8876.
8908. При исследовании изопроцессов использовался закрытый сосуд переменного объема, заполненный аргоном и соединенный с манометром. Объем сосуда медленно уменьшают, сохраняя температуру аргона в нем неизменной. Как изменятся при этом внутренняя энергия аргона в сосуде и концентрация его молекул?
Для каждой величины определите соответствующий характер изменения:
1) не изменится
2) уменьшится
3) увеличится


P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8908.
8940. В ходе адиабатного процесса внутренняя энергия 1 моль разреженного гелия увеличивается. Как изменяются при этом температура гелия и его давление?
Для каждой величины определите соответствующий характер изменения:
1) не изменится
2) уменьшится
3) увеличится


P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8940.
8972. Установите соответствие между процессами в идеальном газе и значениями физических величин, характеризующих эти процессы (( Delta U ) – изменение внутренней энергии; ( A ) работа газа, ( nu ) – количество газа).
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
ПРОЦЕССЫ
А) изотермическое сжатие при ( nu = const )
Б) изобарное расширение при ( nu = const )
ЗНАЧЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН
1) ( Delta U > 0,~A = 0 )
2) ( Delta U > 0,~A > 0 )
3) ( Delta U = 0,~A > 0 )
4) ( Delta U = 0,~A

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 8972.
9004. Установите соответствие между процессами в идеальном газе и значениями физических величин, характеризующих эти процессы (( Delta U ) – изменение внутренней энергии; ( A ) – работа газа, ( upsilon ) – количество газа).
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
ПРОЦЕССЫ
А) адиабатическое сжатие при ( nu = const )
Б) изохорное нагревание при ( nu = const )
ЗНАЧЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН
1) ( Delta U > 0,~A = 0 )
2) ( Delta U > 0,~A > 0 )
3) ( Delta U = 0,~A > 0 )
4) ( Delta U > 0,~A

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 9004.
9036. Температуру холодильника теплового двигателя, работающего по циклу Карно, увеличили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД теплового двигателя и количество теплоты, отданное газом за цикл холодильнику?
Для каждой величины определите соответствующий характер изменения:
1) не изменилась
2) уменьшилась
3) увеличилась


P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса – 9036.
Для вас приятно генерировать тесты, создавайте их почаще
Источник
30. Молекулярная физика (расчетная задача)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Воздушный шар, оболочка которого имеет массу (M) = 145 кг и объём (V) = 230 м(^3), наполняется при нормальном атмосферном давлении горячим воздухом, нагретым до температуры (t) = 265 (^{circ})С. Определите максимальную температуру (t_o) окружающего воздуха, при которой шар начнёт подниматься. Оболочка шара нерастяжима и имеет в нижней части небольшое отверстие (см. рисунок).
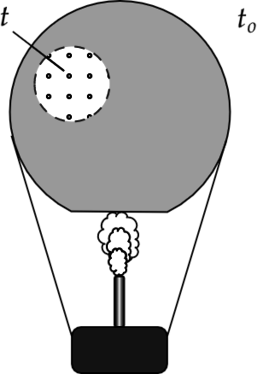
“Демоверсия 2019”
Покажем на рисунке все силы, действущие на воздушный шар и введем вертикальную ось (y):
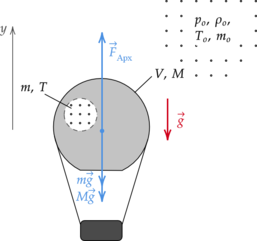
Рассмотрим предельный случай, когда шар вот-вот оторвется от поверхности земли, и запишем для него второй закон Ньютона: [vec{F}_text{Арх} + mvec{g} +Mvec{g} = 0] где (F_text{Арх}) — выталкивающая сила, (m) — масса горячего воздуха, (g) — ускорение свободного падения.
Спроецируем второй закон Ньютона на ось (y), направленную вертикально вверх: [; ; ; ; F_text{Арх} – mg-Mg = 0 ; ; ; ; (1)] Выталкивающая сила равна: [; ; ; ; F_text{Арх} = rho_o gV ; ; ; ; (2)] где (rho_o) — плотность холодного воздуха, (V) — объем шара.
Подставим (2) в (1) и разделим на (g): [; ; ; ; rho_o V – m – M = 0 ; ; ; ; (3)] Заметим, что (rho_o V = m_o), где (m_o) — масса холодного воздуха.
Тогда уравнение (3) будет иметь вид: [; ; ; ; m_o – m – M = 0 ; ; ; ; (4)] Чтобы найти массы горячей и холодного воздуха, запишем для них уравнение Менделеева – Клапейрона: [; ; ; ; p_oV = dfrac{m}{Mr}RT ; ; ; Rightarrow ; ; ; m = dfrac{p_o VMr}{RT} ; ; ; ; (5)] [; ; ; ; p_oV = dfrac{m_o}{Mr}RT_o ; ; ; Rightarrow ; ; ; m_o = dfrac{p_o VMr}{RT_o} ; ; ; ; (6)] где (p_o) — атмосферное давление, (Mr) — молярная масса воздуха, (R) — универсальная газовая постоянная, (T) (T_o) — абсолютные температуры горячего и холодного воздуха соответственно.
Подставим (5), (6) в (4) и выразим максимальную температуру окружающего воздуха, при которой шар начнет подниматься: [dfrac{p_o VMr}{RT_o} – dfrac{p_o VMr}{RT} – M = 0 ; ; ; / :dfrac{p_o VMr}{RT}] [dfrac{1}{T_o} – dfrac{1}{T} – dfrac{MR}{p_oVMr} = 0] [T_o=dfrac{mu p_oVT}{mu p_oV+MRT}] [T_o = dfrac{0,029text{ кг/моль}cdot10^5text{ Па}cdot230text{ м}^3cdot(265+273)text{ К}}{0,029text{ кг/моль}cdot10^5text{ Па}cdot230text{ м}^3+145text{ кг}cdot8,31text{ Дж/(моль$cdot$К)}cdot(265+273)text{ К}}approx273 text{ К}=0^{circ}text{С}]
Ответ: 0 ∘С (273 К)
В теплоизолированном сосуде в начальный момент находится одноатомный газ при температуре (T_o) = 300 К и кусочек железа массой (m) = 2 кг, нагретый до температуры (T_1) = 500 К. Начальное давление газа (p_o) = 10(^5) Па, его объем (V_o) = 10000 см(^3), удельная теплоемкость железа (c) = 0,45 кДж/(кг(cdot)К). Найдите давление газа в равновесном состоянии, считая объем газа неизменным.
Так как по условию задачи система замкнута, то внутренняя энергия ее неизменна. Поэтому равновесное состояние системы будет устанавливаться при передаче тепла газу от более горячего куска железа. По первому закону термодинамики: [Delta U=Q-A,] где (Delta U) — изменение внутренней энергии, (Q) — количество теплоты, которое подводили к телу, (A) — работа газа.
В данном случае работа газа равна нулю, так как (V=const). Уравнение теплового баланса в этом случае имеет вид: [dfrac{3}{2}nu R(T-T_o)=cm(T_1-T), hspace{7 mm} (1)] где (nu) — количество вещества газа, (R) — универсальная газовая постоянная.
Запишем уравнение Менделеева – Клапейрона: [p_oV_o=nu R T_o] Выразим отсюда: [hspace{5 mm} nu R=dfrac{p_oV_o}{T_o} hspace{7 mm} (2)] Выразим из (1) температуру газа (T): [T=dfrac{cmT_1+1,5nu RT_0}{cm+1,5nu R}hspace{5 mm} (3)] Так как объем постоянен и количество вещества газа не меняется, то по закону Шарля: [dfrac{p_1}{T_1} = dfrac{p_o}{T_o}hspace{3 mm} Rightarrow hspace{3 mm} p_1=p_ocdotdfrac{T}{T_o}hspace{5 mm} (4)] Подставим (3) в (4): [p_1=p_ocdotdfrac{cmT_1+1,5nu RT_o}{T_o(cm+1,5nu R)}hspace{5 mm} (5)] Подставим (2) в (5): [p_1=p_ocdotdfrac{cmT_1+1,5dfrac{p_oV_o}{T_o}T_o}{T_oleft(cm+1,5dfrac{p_oV_o}{T_o}right)} = p_ocdotdfrac{cmT_1+1,5p_oV_o}{T_ocm+1,5p_oV_o}] Найдем давление газа в равновесном состоянии: [p_1 = 10^5 text{ Па}cdotdfrac{450text{ Дж}/(text{кг}cdottext{К})cdot2 text{ кг} cdot500 text{ К}+1,5cdot10^5text{ Па}cdot10^{-2}text{ м$^3$}}{300text{ К}cdot450text{ Дж}/(text{кг}cdottext{К})cdot2 text{ кг}+1,5cdot10^5text{ Па}cdot10^{-2}text{ м$^3$}} approx 166 text{ кПа}]
Ответ: 166 кПа
Два литра жидкого аргона находится при температуре своего кипения -186 (^{circ})С. Какое количество теплоты нужно сообщить этому количеству аргона для того, чтобы при постоянном давлении перевести его в газ, имеющий температуру 0 (^{circ})С? Плотность жидкого аргона 1400 кг/м(^3), его удельная теплота испарения 87 кДж/кг.
Чтобы перевести аргон в газ, имеющий температуру 0 (^circ)С, сначала необходимо перевести его из жидкого состояния в газообразное, а затем нагреть до нужной температуры.
Общее количество теплоты (Q), которое необходимо для этого, будет складываться из двух составяющих: [; ; ; ; Q = Q_1 + Q_2 ; ; ; ; (1)] Количество теплоты, которое потребуется для парообразования аргона: [; ; ; ; Q_1=rm, ; ; ; ; (2)] где (m) — масса аргона, (r) — удельная теплота испарения.
Когда аргон превратится в газ, мы будем его рассматривать как идеальный одноатомный газ. Значит, для нагрева аргона до 0 (^{circ}) С запишем перове начало термодинамики: [Q_2=Delta U+A,] где (Q_2) — количество теплоты, необходимое для нагревания, (Delta U) — изменение внутренней энергии аргона, (A) — работа аргона.
[Q_2=dfrac{3}{2}nu RDelta T+p(V_2-V_1), hspace{7 mm} (3)] где (nu) — количество вещества, (Delta T) — изменение температуры, (p) — давление, (V_2) и (V_1) — конечное и начальное давлени газа, а в дальнейшнем (mu) — молярная масса газа, (rho) — плотность аргона.
По уравнению Клапейрона — Менделеева: [p(V_2-V_1)=nu R Delta T hspace{7 mm} (4)] Подставим (4) в (3): [Q_2=dfrac{3}{2}nu RDelta T+nu RDelta T] [; ; ; ; Q_2 = dfrac{5}{2}nu RDelta T ; ; ; ; (5)] Подставим (2), (5) в (1): [Q=rm+dfrac{5}{2}nu RDelta T] Количество вещества аргона можно найти по формуле: (nu = dfrac{m}{mu}), где (mu) — молярная масса аргона.
Массу аргона можно найти, зная его плотность и объем: (m = rho V).
С учетом этого: [Q=rrho V+dfrac{5}{2}cdotdfrac{rho V}{mu}RDelta T] [Q=87cdot10^3text{ кДж/кг}cdot2cdot10^{-3}text{ м$^3$}cdot1400text{ кг/м$^3$} +dfrac{5}{2}cdotdfrac{1400text{ кг/м$^3$}cdot2cdot10^{-3}text{ м$^3$}}{40cdot10^{-3}text{кг/моль}}cdot8,31cdot186^circtext{C} approx 591 text{ кДж}]
Ответ: 591 кДж
Когда легковой автомобиль едет с постоянной скоростью по горизонтальному шоссе, расход бензина составляет (mu_1) = 7 л/100 км. Каков будет расход бензина (mu_2), если этот автомобиль поедет с той же скоростью вверх по наклонному участку шоссе, образующему угол (alpha) = 0,01 рад с горизонтом? Качество дорожного покрытия на горизонтальном и наклонном участках шоссе одинаково. Масса автомобиля (M) = 1000 кг, коэффициент полезного действия двигателя (eta = 30%), удельная теплота сгорания бензина (q) = 42 МДж/кг, плотность бензина (rho) = 0,7 кг/л. При расчетах положить (sin alpha approx alpha).
По условию задачи КПД двигателя автомобиля равен 30%. Это означает, что только 30% от выделевшегося количества теплоты пойдет на совершение работы по перемещению автомомбиля: [; ; ; ; A = 0,3Q ; ; ; ; (1)] Количество теплоты, которое выделится при сгорании бензина, равно: [; ; ; ;Q = qm ; ; ; ; (2)] где (m) — масса сгоревшего бензина.
Массу бензина можно найти, зная его плотность: [; ; ; ; rho = dfrac{m}{V} ; ; ; Rightarrow ; ; ; m = rho V ; ; ; ; (3)] где (V) — объем сгоревшего бензина.
Зная расход бензина и пройденное расстояние, найдем объем израсходованного бензина: [; ; ; ;V = mu l ; ; ; ;(4)] Подставим последовательно (4), (3), (2) в (1): [; ; ; ;A = 0,3qrhomu l ; ; ; ; (5)] В то же время работа при перемещении автомобиля на расстояние (l) по определению равна: [A = Flcosalpha_o] где (F) — модуль равнодействующей всех сил, действующих на автомобиль, (alpha_o) — угол между направлением силы и направлением перемещения.
В рассматриваемых случаях и для горизонтального движения и для движения под углом к гори3 зонту (cosalpha = 1): [; ; ; ; A = Fl ; ; ; ;(6)] 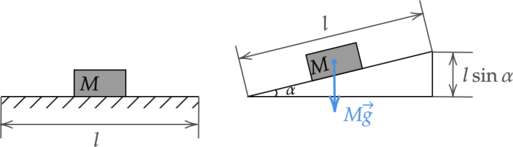
Рассмотрим движение автомобиля по горизонтальному участку шоссе.
В этом случае работа, совершенная двигателем, по величине равна работе сил сопротивления.
Исходя из формул (5) и (6), получаем, что: [0,3qrhomu_1 l = Fl] Выразим отсюда силу (F): [; ; ; ; F = 0,3qrhomu_1 ; ; ; ; (7)] Рассмотрим движение автомобиля по наклонному участку шоссе той же длины.
В этом случае работа двигателя равна сумме величины работы сил сопротивления и изменения (приращения) потенциальной энергии автомобиля в поле силы тяжести: [A = Fl + Mglsinalpha] С учетом формулы (5) имеем, что: [0,3qrhomu_2 l = Fl + Mglsinalpha] Выразим отсюда силу (F): [; ; ; ; F = 0,3qrhomu_2 – Mgsinalpha ; ; ; ; (8)] Приравняем (7) и (8) с учетом того, что по условию (sinalpha approx alpha), и выразим искомый расход бензина: [0,3qrhomu_1 = 0,3qrhomu_2 – Mgsinalpha] [mu_2 = mu_1 + dfrac{Mgalpha}{0,3rho q}] [mu_2 = 7(text{ л/$100$ км}) + dfrac{1000text{ кг}cdot10text{ м/с}^2cdot0,01}{0,3cdot0,7text{ кг/л}cdot 42cdot10^6text{ Дж/кг}}cdot10^5 approx 8,13text{ л/100 км}]
Ответ: 8,13 л/100 км
Мальчик решил подняться в воздух на воздушных шарах с гелием. Известно, что мальчик весит 40 кг, а на улице нормальное атмосферное давление и температура 27 (^{circ})С. Учитывая, что объем одного шара составляет 10 литров, найдите, сколько потребуется шаров для такого путешествия. Массой оболочки шаров и объемом мальчика пренебречь.
Cила тяжести, действующая на систему, уравновешивается силой Архимеда.
Рассмотрим предельный случай, когда мальчик на воздушных шарах вот-вот оторвется от поверхности земли, и запишем второй закон Ньютона для данной системы: [vec{F}_text{Арх} + Mvec{g} + nmvec{g} = 0] где (M) — масса мальчика, (m) — масса гелия в одном шарике, (n) — количество шаров, (g) — ускорение свободного падения.
Спроецируем второй закон Ньютона на вертикальную ось, направленную вверх: [F_text{Арх} – Mg – nmg = 0] [; ; ; ; F_text{Арх} = Mg + nmg ; ; ; ; (1)] Сила Архимеда равна: [F_text{Арх} = rho_o gnV] где (rho_o) — плотность воздуха, (V) — объем одного шарика.
Подставим (2) в (1): [rho_o gnV = Mg + nmg] [; ; ; ; rho_o nV = M + nm ; ; ; ; (3)] Запишем уравнение Менделеева-Клапейрона для воздуха: [; ; ; ; p_oV_o = dfrac{m_o}{mu_o} RT_o ; ; ; ; (4)] где (p_o) — атмосферное давление, (V_o) — объем, занимаемый воздухом, (m_o) — (mu_o) — масса воздуха, (R) — универсальная газовая постоянная, (T_o) — абсолютная температура воздуха.
Плотность воздуха равна: [; ; ; ; rho_o = dfrac{m_o}{V_o} ; ; ; ; (5)] Подставим (5) в (4) и выразим плотность воздуха: [; ; ; ; p_o = dfrac{rho_o}{mu_o}RT_o ; ; ; Rightarrow ; ; ; rho_o = dfrac{p_omu_o}{RT_o} ; ; ; ; (6)] Найдем массу гелия в одном шарике из уравнения Менделеева-Клапейрона: [; ; ; ; p_o V = dfrac{m}{mu}RT_o ; ; ; Rightarrow ; ; ; m = dfrac{p_o Vmu}{RT_o} ; ; ; ; (7)] где (m) — масса гелия, (mu) — молярная масса гелия.
Подставим (6), (7) в (3) и выразим количество шариков: [M + ndfrac{p_o Vmu}{RT_o} = dfrac{p_o mu_o}{RT_o}nV] [n = dfrac{MRT_o}{p_o V(mu_o – mu)}] [n = dfrac{40text{ кг}cdot8,31text{Дж/(моль$cdot$К)}cdot300text{ К}}{10^5text{ Па}cdot10^{-2}text{ м}^3cdot(29-4)cdot10^{-3} text{кг/моль}}=3989]
Ответ: 3989
Воздушный шар, оболочка которого имеет массу (M) = 145 кг и объём (V) = 230 м(^3), наполняется при нормальном атмосферном давлении горячим воздухом, нагретым до температуры (t) = 265 (^{circ})С. Определите максимальную температуру (t_o) окружающего воздуха, при которой шар начнёт подниматься. Оболочка шара нерастяжима и имеет в нижней части небольшое отверстие (см. рисунок). 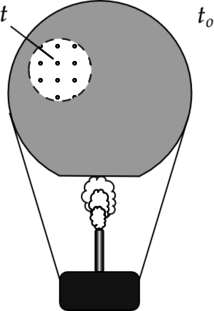
Покажем на рисунке все силы, действущие на воздушный шар и введем вертикальную ось (y):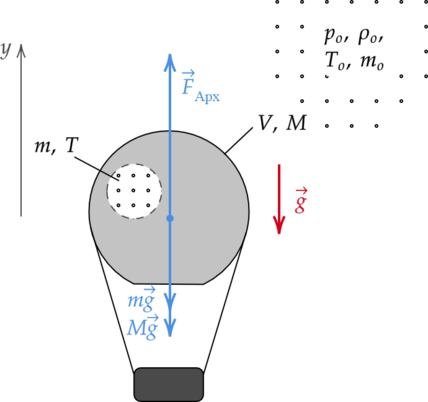
Рассмотрим предельный случай, когда шар вот-вот оторвется от поверхности земли, и запишем для него второй закон Ньютона: [vec{F}_text{Арх} + mvec{g} +Mvec{g} = 0] где (F_text{Арх}) — выталкивающая сила, (m) — масса горячего воздуха, (g) — ускорение свободного падения.
Спроецируем второй закон Ньютона на ось (y), направленную вертикально вверх: [; ; ; ; F_text{Арх} – mg-Mg = 0 ; ; ; ; (1)] Выталкивающая сила равна: [; ; ; ; F_text{Арх} = rho_o gV ; ; ; ; (2)] где (rho_o) — плотность холодного воздуха, (V) — объем шара.
Подставим (2) в (1) и разделим на (g): [; ; ; ; rho_o V – m – M = 0 ; ; ; ; (3)] Заметим, что (rho_o V = m_o), где (m_o) — масса холодного воздуха.
Тогда уравнение (3) будет иметь вид: [; ; ; ; m_o – m – M = 0 ; ; ; ; (4)] Чтобы найти массы горячей и холодного воздуха, запишем для них уравнение Менделеева – Клапейрона: [; ; ; ; p_oV = dfrac{m}{Mr}RT ; ; ; Rightarrow ; ; ; m = dfrac{p_o VMr}{RT} ; ; ; ; (5)] [; ; ; ; p_oV = dfrac{m_o}{Mr}RT_o ; ; ; Rightarrow ; ; ; m_o = dfrac{p_o VMr}{RT_o} ; ; ; ; (6)] где (p_o) — атмосферное давление, (Mr) — молярная масса воздуха, (R) — универсальная газовая постоянная, (T) (T_o) — абсолютные температуры горячего и холодного воздуха соответственно.
Подставим (5), (6) в (4) и выразим максимальную температуру окружающего воздуха, при которой шар начнет подниматься: [dfrac{p_o VMr}{RT_o} – dfrac{p_o VMr}{RT} – M = 0 ; ; ; / :dfrac{p_o VMr}{RT}] [dfrac{1}{T_o} – dfrac{1}{T} – dfrac{MR}{p_oVMr} = 0] [T_o=dfrac{mu p_oVT}{mu p_oV+MRT}] [T_o = dfrac{0,029text{ кг/моль}cdot10^5text{ Па}cdot230text{ м}^3cdot(265+273)text{ К}}{0,029text{ кг/моль}cdot10^5text{ Па}cdot230text{ м}^3+145text{ кг}cdot8,31text{ Дж/(моль$cdot$К)}cdot(265+273)text{ К}}approx273 text{ К}=0^{circ}text{С}]
Ответ: 0 ∘С (273 К)
Сосуд объемом (V) л, содержащий (nu) моль воздуха при давлении (p) Па и температуре (T_o) К, сверху заткнут пробкой массой (m) кг с площадью (S) см(^2). Найдите на какую величину надо увеличить температуру газа, чтобы пробка вылетела из сосуда, если коэффицент трения пробки о стенки сосуда равен (mu), а атмосферное давление равно (p_o).
Запишем 2 закон Ньютона для предельного случая, когда пробка вот-вот вылетит из сосуда: [; ; ; ; F = F_text{тяж}+F_text{тр}+F_text{атм}, ; ; ; ; ; (1)] где (F) — сила, с которой газ воздействует на пробку, (F_text{тяж}) — сила тяжести, действующая на пробку , (F_text{тр}) — сила трения пробки о стенки сосуда, (F_text{атм}) — сила давления атмосферы на пробку.
Сила, с которой газ воздействует на пробку, равна: [; ; ; ; p=dfrac{F}{S} ; ; ; Rightarrow ; ; ; F=pS ; ; ; ; (2)] По уравнению Клайперона – Менделеева: [; ; ; ; pV=nu R T ; ; ; Rightarrow ; ; ; p=dfrac{nu R T}{V},; ; ; ; (3)] где (T) — абсолютная температура газа, (Delta T) — изменение температуры газа.
Подставим (3) в (2): [; ; ; ; F = dfrac{nu R T}{V}S ; ; ; ; (4)] Сила давления атмосферы на пробку равна: [; ; ; ; F_text{атм}=p_oS ; ; ; ; (5)] Силу тяжести и силу трения найдем по формулам: [; ; ; ; F_text{тяж}=mg ; ; ; (6) ; ; ; ; ; ; ; ; ; ; ; F_text{тр}=mu mg, ; ; ; (7)] где (g) — ускорение свободного падения.
Подставим (4), (5), (6), (7) в (1) и получим: [; ; ; ; S dfrac{nu R T}{V} = mg +mu m g +p_o S ; ; ; ; (8)] Конечная температура газа равна: [; ; ; ; T=T_o + Delta T ; ; ; ; (9)] Подставим (9) в (8) и выразим (Delta T), на которую нужно увеличить температуру газа, чтобы пробка вылетела: [S dfrac{nu R (T_o + Delta T)}{V} = mg +mu m g +p_o S] [Delta T =dfrac{V}{nu R}left(dfrac{mg}{S}+dfrac{mu m g }{S}+p_oright)-T_o]
Ответ: $Delta T =dfrac{V}{nu R}left(dfrac{mg}{S}+dfrac{mu m g }{S}+p_oright)-T_o$
Источник
