В сосуды налили по 400 г воды при

Задачи на количество теплоты с решениями

Формулы, используемые на уроках «Задачи на количество теплоты,
удельную теплоемкость».

1 г = 0,001 кг;     1 т = 1000 кг;    1 кДж = 1000 Дж;    1 МДж = 1000000 Дж

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
 В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?

При решении задачи нужно учесть, что оба тела — и котёл, и вода — будут нагреваться вместе. Между ними происходит теплообмен. Их температуры можно считать одинаковыми, т. е. температура котла и воды изменяется на 100 °С — 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми. Ведь их массы и удельные теплоёмкости различны.

Задача № 2.
 Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.

Задача № 3.
 Стальная деталь массой 3 кг нагрелась от 25 до 45 °С. Какое количество теплоты было израсходовано?

Задача № 4.
 В сосуде содержится 3 л воды при температуре 20 °С. Сколько воды при температуре 45 °С надо добавить в сосуд, чтобы в нём установилась температура 30 °С? Необходимый свободный объём в сосуде имеется. Теплообменом с окружающей средой пренебречь

Задача № 5.
 На сколько градусов изменилась температура чугунной детали массой 12 кг, если при остывании она отдала 648000 Дж теплоты?

Задача № 6.
 По графику определите удельную теплоёмкость образца, если его масса 50 г.

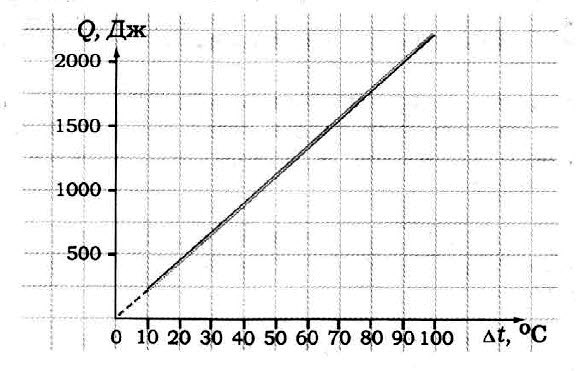
Задача № 7.
 Для нагревания медного бруска массой 3 кг от 20 до 30 °С потребовалось 12000 Дж теплоты. Какова удельная теплоемкость меди?

Задача № 8.
 Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей 2,1 кДж энергии. Чему равна удельная теплоемкость камня?

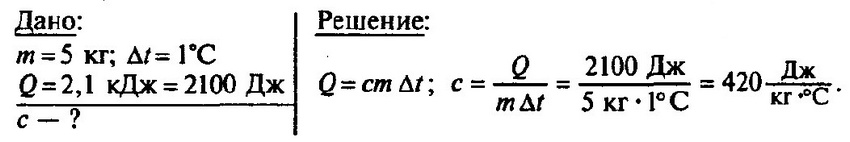
Задача № 9.
 Какое количество теплоты потребуется для нагревания на 1 °С воды объемом 0,5 л; олова массой 500 г; серебра объемом 2 см3; стали объемом 0,5 м3; латуни массой 0,2 т?

Задача № 10.
 Какое количество теплоты получили алюминиевая кастрюля массой 200 г и находящаяся в ней вода объемом 1,5 л при нагревании от 20 °С до кипения при температуре 100 °С?

Задача № 11.
 а) Воздух, заполняющий объем 0,5 л в цилиндре с легким поршнем, нагрели от 0 до 30 °С при постоянном атмосферном давлении. Какое количество теплоты получил воздух? 
б) В порожнем закрытом металлическом баке вместимостью 60 м3 под действием солнечного излучения воздух нагрелся от 0 до 20 °С. Как и на сколько изменилась внутренняя энергия воздуха в баке? (Удельная теплоемкость воздуха при постоянном объеме равна 720 Дж/кг-°С.)

Задача № 12.
  ОГЭ
 Металлический цилиндр массой m = 60 г нагрели в кипятке до температуры t = 100 °С и опустили в воду, масса которой mв = 300 г, а температура tв = 24 °С. Температура воды и цилиндра стала равной Θ = 27 °С. Найти удельную теплоёмкость металла, из которого изготовлен цилиндр. Удельная теплоёмкость воды св = 4200 Дж/(кг К).

Задача № 13.
 В теплоизолированном сосуде сначала смешивают три порции воды 100 г, 200 г и 300 г с начальными температурами 20 °C, 70 °C и 50 °C соответственно. После установления теплового равновесия в сосуд добавляют новую порцию воды массой 400 г при температуре 20 °C. Определите конечную температуру в сосуде. Ответ дайте в °C, округлив до целого числа. Теплоёмкостью калориметра пренебрегите.

Решение.

Ответ: 39 °С.

Задача № 14. (повышенной сложности)
 Стальной шарик радиусом 5 см, нагретый до температуры 500 ˚С, положили на лед, температура которого 0 ˚С. На какую глубину погрузится шарик в лед? (Считать, что шарик погрузился в лед полностью. Теплопроводностью шарика и нагреванием воды пренебречь.)

Дано: R = 0,05 м;   t1 = 500 ˚С;   t2 = 0 ˚С;
ρ1 (плотность стали) = 7800 кг/м3.;
ρ2 (плотность льда) = 900 кг/м3.
c (удельная теплоемкость стали) = 460 Дж/кг •˚С,
λ (удельная теплота плавления льда) = 3,3 • 105 Дж/кг,

Найти: h – ?

Краткая теория для решения Задачи на количество теплоты.

Конспект урока «Задачи на количество теплоты».

Посмотреть конспект урока по теме «Количество теплоты. Удельная теплоемкость»

Следующая тема: «ЗАДАЧИ на сгорание топлива с решениями».