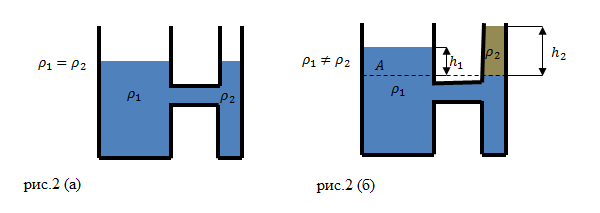
В сосуды налиты разные жидкости
Определение
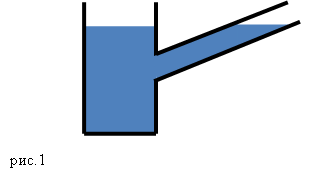
Соединенные между собой сосуды называют сообщающимися.
В таких сосудах жидкость имеет возможность перетекать из одной емкости в другую (рис.1). Форма сообщающихся сосудов может быть самая разная.
Допустим, что в сообщающиеся сосуды налита однородная жидкость, то в этих сосудах жидкость устанавливается на одном уровне, если давление над поверхностью жидкости одинаково, и не важно какую форму имеют сосуды. В неподвижной жидкости давление ($p$) на одном уровне в сообщающихся сосудах является равным, так как мы знаем, что:
[p=rho gh left(1right),]
где $rho $ – плотность жидкости; $g$ – ускорение свободного падения; $h$ – высота столба жидкости. Так как давление на одном уровне жидкости одинаково, то равными будут и высоты столбов жидкости.
Жидкости разной плотности в сообщающихся сосудах
Допустим, что в сообщающиеся сосуды налили жидкость разной плотности (рис.2(б)). В состоянии равновесия жидкостей, их уровни не будут находиться на одном уровне (высоты столбов жидкости равными не будут).

Жидкости в сосудах находятся в равновесии. Давления на уровне A (граница раздела разных жидкостей) (рис. 2 (б)) равны:
[{rho }_1gh_1={rho }_2gh_2left(2right),]
где ${rho }_1$ и ${rho }_2$ – плотности жидкостей. Найдем отношение высот столбов жидкостей в сосудах:
[frac{h_1}{h_2}=frac{{rho }_2}{{rho }_1}left(3right).]
Формула (3) говорит о том, что в сообщающихся сосудах высоты столбиков жидкости над уровнем их раздела обратно пропорциональны плотностям этих жидкостей. При одинаковом давлении над поверхностями жидкостей, высота столба жидкости с меньшей плотностью будет больше, чем высота столба более плотной жидкости.
Гидравлический пресс и другие примеры использования сообщающихся сосудов
В технике сообщающиеся сосуды используют часто. Например, существует такое устройство, как гидравлический пресс. Его изготавливают из двух цилиндров разного радиуса, в которых находятся поршни (рис.3). Сообщающиеся сосуды пресса обычно заполняют минеральным маслом.
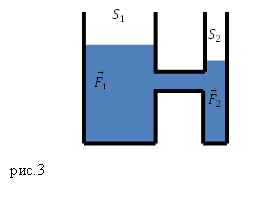
Пусть площадь первого поршня, к которому прикладывают силу ${overline{F}}_1,$ равна $S_1$, площадь второго $S_2$, к нему приложена сила ${overline{F}}_2$. Давление, которое создает первый поршень равно:
[p_1=frac{F_1}{S_1}left(4right).]
Второй поршень давит на жидкость:
[p_2=frac{F_2}{S_2}left(5right).]
Если система находится в состоянии равновесия, то по закону Паскаля давления $p_1$ и $p_2$ равны:
[frac{F_1}{S_1}=frac{F_2}{S_2}left(6right).]
Получим:
[F_1=F_2frac{S_1}{S_2}(7)]
величина первой силы больше модуля силы $F_2$ в $frac{S_1}{S_2}$ раз. Это означает, что при помощи гидравлического пресса, прикладывая небольшую силу к поршню малого сечения, можно получить большую по величине силу, которая будет действовать на большой поршень.
По принципу сообщающихся сосудов, в особенности раньше, действовал водопровод. Такой водопровод сейчас еще можно наблюдать на дачных участках. На относительно большой высоте устанавливается бак с водой, от бака идут водопроводные трубы, закрываемые кранами. Давление у кранов соответствует давлению столба воды, который равен разности высот уровень крана – уровень воды в баке.
Принципом сообщающихся сосудов пользовались, когда проектировали фонтаны, работающие без насосов, шлюзы на реках и каналах.
Примеры задач с решением
Пример 1
Задание. Имеются два цилиндрических сосуда. Высота столба жидкости в одном равна $h_1$, в другом $h_2$. Эти сосуды соединяют трубкой. Насколько изменится высота столба жидкости в левом сосуде, если площадь поперечного сечения его $S_1>S_2$ , $S_2$ – площадь сечения правого сосуда. Объемом трубки пренебречь.
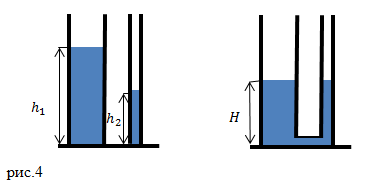
Решение. После того как сосуды соединили, они стали сообщающимися. Часть жидкости из левого сосуда перетечет в правый. Так как жидкость в правом и левом сосудах одна и та же, то уровни жидкости в обоих сосудах будут находиться на одном уровне, то есть высота столбиков жидкости станет равна $H$ в обоих коленах емкости. Определим, какой объем воды перетечет из левого колена в правое:
[Delta V_1=left(h_1-Hright)S_{1 }left(1.1right),]
где $S_{1 }$ – площадь поперечного сечения левого сосуда (сосуда из которого вытекает жидкость). В правом сосуде эта жидкость займет объем равный:
[Delta V_2=left(H-h_2right)S_{2 }left(1.2right),]
где $S_{2 }$ – площадь поперечного сечения правого сосуда. Так как мы считаем, что жидкость не сжимаема, то имеем:
[Delta V_1=Delta V_2left(1.3right).]
Приравниваем правые части выражений (1.2) и (1.1), выражаем высоту столбиков жидкости в правой и левой части сообщающихся сосудов:
[left(h_1-Hright)S_{1 }=left(H-h_2right)S_{2 }to H=frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }} left(1.4right).]
Используя выражение (1.4), изменение высоты жидкости в левом колене, получим равным:
[Delta h=h_1-H=h_1-frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }}=frac{h_1S_1+h_1S_2-h_1S_{1 }-S_{2 }h_2}{S_1+S_{2 }}=] [=frac{h_1S_2-S_{2 }h_2}{S_1+S_{2 }}=frac{h_1-h_2}{S_1+S_{2 }}S_2.]
Ответ. $Delta h=frac{h_1-h_2}{S_1+S_{2 }}S_2$
Пример 2
Задание. Какой будет сила давления на большой поршень (площадью $S_1$) гидравлического пресса, если площадь его малого поршня равна $S_2$, при этом на него действует сила равная $F_2$?
Решение. В теоретическом разделе сказано, что гидравлический пресс представляет собой систему из сообщающихся сосудов (рис.3). Из закона Паскаля следует, что, прикладывая небольшую силу ($F_2$) к поршню малого сечения ($S_2$) пресса, можно получить большую по величине силу, которая будет действовать на большой поршень ($S_1$):
[F_1=F_2frac{S_1}{S_2}(2.1)]
Ответ. $F_1=F_2frac{S_1}{S_2}$
Читать дальше: условия плавания тел.
Источник
Определение
Сообщающиеся сосуды – сосуды, соединенные между собой или имеющие общее дно.
Уровень жидкости в сообщающихся сосудах одинаков и располагается горизонтально, если:
- в сосуды налита однородная жидкость
- поверхности жидкости открыты
ни один из сосудов не является капилляром (очень узкой трубкой)
в жидкости нет пузырьков с воздухом.
Разные по плотности не смешивающиеся жидкости в сообщающихся сосудах
Если в сообщающихся сосудах находятся неоднородные жидкости, то, согласно закону Паскаля, более плотная жидкость будет оказывать большее давление на дно сосуда и в стороны. Поэтому она будет вытеснять часть жидкости с меньшей плотностью. Равновесие наступит тогда, когда давление столба с более плотной жидкостью сравняется с давлением столба, образованного из двух жидкостей.
По закону Паскаля на любом горизонтальном уровне:
p1 = p2
ρ1gh1 = ρ2gh2
Следовательно:
h2h1=ρ1ρ2
Следовательно, высота столба менее плотной жидкости во столько раз выше высоты столба более плотной жидкости, во сколько более плотная жидкость плотнее менее плотной.
Пример №1. В широкую U-образную трубку с вертикальными прямыми коленами налиты керосин плотностью ρ1 = 800 кг/м3 и вода плотностью ρ2 = 1000 кг/м3 (см. рисунок). На рисунке b = 10 см, H = 30 см. Определите расстояние h.
10 см = 0,1 м
20 см = 0,3 м
Жидкость находится в равновесии. С учетом того, что в первом колене содержится сразу две жидкости:
ρ1g(H – b) + ρ2gb = ρ2gh
Или:
ρ1(H – b) + ρ2b = ρ2h
Отсюда:
h=ρ1(H−b)+ρ2bρ2=800(0,3−0,1)+1000·0,11000=0,26 (м)
Гидравлический пресс
Определение
Гидравлический пресс – простой механизм, дающий выигрыш в силе. Он представляет собой сообщающиеся сосуды разного сечения.
В основе действия гидравлического пресса лежит закон Паскаля. Так как высоты столбов равны, давления в колене малого и большого сечения тоже равны:
pм = pб
Следовательно:
FмSм=FбSб
Fм – сила, действующая на малый поршень (совершает полную работу), Fб – сила, действующая на большой поршень (совершает полезную работу), Sм – площадь малого поршня, Sб – площадь большого поршня.
Работа поршней (без потерь энергии):
Aм = Aб
Fмhм = Fбhб
hм – вертикальное перемещение малого поршня, hб – перемещение большого поршня.
Равенство объемов жидкостей при движении поршней:
Sмhм = Sбhб
КПД (есть потери энергии):
η=AбAм·100%=FбhбFмhм·100%=pбpм·100%
Пример №2. К малому поршню гидравлического пресса приложена сила 10 Н, под действием которой за один ход он опускается на 25 см, вследствие чего большой поршень поднимается на 5 мм. Какая сила давления передается при этом на большой поршень?
25 см = 0,25 м
5 мм = 0,005 м
Так как работа поршней одинакова:
Fмhм = Fбhб
Отсюда:
Fб=Fмhмhб=10·0,250,005=500 (Н).
Атмосферное давление
Атмосфера – воздушная оболочка Земли. Она существует благодаря земному притяжению и беспорядочному движению молекул в газообразном состоянии. В состав атмосферы входят азот, кислород и другие газы. Атмосфера не имеет четкой границы, а плотность воздуха уменьшается с высотой.
Определение
Атмосферное давление – давление «воздушного океана», которое также уменьшается с высотой.
Ртутный барометр
Определение
Ртутный барометр – прибор для определения атмосферного давления, созданный Торричелли. Состоит из стеклянной трубки, запаянной с одного конца, длиной 1 м, заполненной ртутью, а также из широкого сосуда, в который выливается ртуть после поворота трубки.
По свойству сообщающихся сосудов:
pатм = pртути (мм рт. ст.).
Формула для определения атмосферного давления (в паскалях):
pатм = pртgh
pатм – атмосферное давление, pрт – плотность ртути (13600 кг/м3), g – ускорение свободного падения (9,8 м/с2 или округленно – 10 м/с2), h – высота ртутного столба (м).
Дополнительные единицы измерения атмосферного давления:
1 мм рт. ст. = 133 Па
1 атм (атмосфера) = 105 Па
Нормальное атмосферное давление равно: p0 = 105 Па.
Пример №3. С какой силой давит воздух на поверхность письменного стола, длина которого 120 см, ширина – 60 см, если атмосферное давление равно 100 кПа?
Сила давления есть произведение давления на площадь. Поэтому:
F = pS = pab = 105∙1,2∙0,6 = 72 кН.
Задание EF18172 В широкую U-образную трубку, расположенную вертикально, налиты жидкости плотностью ρ1 и ρ2 (см. рисунок). Жидкости не смешиваются. На рисунке b = 15 см, h = 30 см, H = 35 см. Отношение плотности ρ1 к плотности ρ2 равно …
Ответ:
а) 0,67
б) 0,75
в) 0,86
г) 1,33
Алгоритм решения
1.Записать исходные данные.
2.Записать условие равновесия неоднородных жидкостей в сообщающихся сосудах.
3.Выполнить решение задачи в общем виде.
4.Вычислить искомую величину, подставив известные значения.
Решение
Запишем исходные данные:
• Уровень жидкости в левом колене: H = 35 см.
• Уровень жидкости в правом колене: h = 30 см.
• Высота столба более плотной жидкости в левом колене: b = 15 см.
Внимание! В данном случае переводить единицы в СИ необязательно, так как на величину отношения они никак не повлияют.
Запишем условие равновесия. Давление на уровне b в обоих коленах должно быть одинаковое. Поэтому:
ρ1g(H – b) = ρ2g(h – b)
Отсюда:
ρ1ρ2=g(h−b)g(H−b)=h−bH−b=30−1535−15=1520=0,75
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF22683 В комнате находится открытая сверху U-образная трубка, в которую налита ртуть (рис. а). Левое колено трубки плотно закрывают пробкой (рис. б), после чего температура в комнате увеличивается. Что произойдёт с уровнями ртути в коленах трубки? Атмосферное давление считать неизменным. Ответ поясните, указав, какие физические явления и закономерности Вы использовали для объяснения.
Алгоритм решения
- Установить, что изменится после того, как одно колено сосуда будет закупорено.
- Установить, что изменится после того, как температура воздуха увеличится.
Решение
Изначально давление, оказываемое атмосферой на поверхность ртути в обоих коленах, равно. Это следует из закона Паскаля и условия равновесия. Когда одно колено сообщающихся сосудов будет закупорено, сначала давление под пробкой будет равно атмосферному давлению. Но при изменении прочих условий уровень жидкостей в коленах не будет одинаков. Это связано с изменением давления, оказываемого на поверхности жидкостей в закупоренном и открытом коленах.
Если же увеличить температуру воздуха, то воздух под пробкой тоже нагреется. От этого его объем увеличится, что приведет к росту давления, которое окажется больше атмосферного на величину, равную ∆p = ρвg∆h. Суммарное давление, оказываемое со стороны закупоренного колена, будет равно сумме атмосферного давления и давления ∆p: pз = pатм + ρвg∆h. Со стороны открытого колена по-прежнему будет оказываться атмосферное давление: pо = pатм. Поэтому избыточное давление под пробкой начнет выталкивать часть ртути из левого колена в правое до тех пор, пока не наступит равновесие. При условии, что диаметр трубок одинаковый, это произойдет тогда, когда уровень ртути в открытой трубке увеличится на высоту ∆h – на ту высоту, на которую понизится уровень ртути в закупоренной трубке.
Ответ: уровень ртути в закрытом колене понизится, а в открытом – понизится.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | ???? Скачать PDF | Просмотров: 540 | Оценить:
Источник
Итоговый тест по темам Давление, Давление в жидкости и газе, Сообщающиеся сосуды для учащихся 7 класса с ответами. Тест состоит из 2 вариантов, в каждом варианте по 15 заданий.
1 вариант
1. На полке стоят тела равной массы. Какое из них производит на неё наименьшее давление?
1) №1
2) №2
3) №3
4) №4
2. Давление твёрдых тел рассчитывают по формуле:
1) m = P/g
2) p = gρh
3) ρ = m/V
4) p = F/S
3. Как называют единицу давления и чему она равна?
1) Ньютон, 1 Н
2) Килограмм, 1 кг
3) Паскаль, 1 Н/м2
4) Километр, 1 км
4. Выразите в паскалях давления 3000 Н/м2 и 1,2 кПа.
1) 3000 Па, 1200 Па
2) 300 Па, 120 Па
3) 30 000 Па, 12 000 Па
4) 3000 Па, 120 Па
5. Рассчитайте давление, которое производит станок 1000 Н, если его опорная часть имеет площадь 0,25 м2.
1) 4 кПа
2) 25 кПа
3) 400 Па
6. Определите давление бочонка с мёдом массой 6 кг, площадь дна которого 300 см2.
1) 200 Па
2) 20 Па
3) 2 кПа
4) 20 кПа
7. Давление воздуха или водяного пара больше при одинаковых условиях?
1) Их давления одинаковы
2) Водяного пара
3) Воздуха
4) Для ответа нужны дополнительные сведения
8. Одинаковые баллоны с природным газом находятся в разных местах: один (№1) – в тёплом помещении, другой (№2) – в холодном, а третий (№3) – на снегу на улице. В каком из них давление газа наименьшее?
1) №1
2) №2
3) №3
4) Давления одинаковы
9. Опусканием поршня создано давление на газ, равное 100 Па. На сколько возросли при этом давления на площадки №1, №2, №3?
1) №1 – 100 Па
2) №2 – давление не изменилось
3) №3 – 200 Па
4) На все площадки давление увеличилось на 100 Па
10. По какой формуле рассчитывают давление жидкости?
1) р = gρh
2) Р = gm
3) m = ρV
4) F = kΔl
11. Найдите давление воды на глубине 1 м.
1) 1 кПа
2) 10 кПа
3) 100 кПа
4) 1000 кПа
12. Брусок помещён в сосуд с водой так, как показано на рисунке. Каково давление воды на нижнюю грань?
1) 5000 Па
2) 1000 Па
3) 500 Па
4) 100 Па
13. В каком из этих сосудов давление жидкости на дно наименьшее?
1) №1
2) №2
3) №3
4) Во всех сосудах одинаково
14. В три одинаковых сосуда налиты доверху такие жидкости: в один (№1) – мёд, в другой (№2) – вода, в третий (№3) – молоко. На дно какого из них будет действовать наибольшее давление?
1) №1
2) №2
3) №3
4) Давления везде одинаковы
15. Главное свойство сообщающихся сосудов заключается в том, что
1) при соединении широкого и узкого сосудов жидкость устанавливается в них на разных уровнях
2) во всех таких сосудах поверхности однородной жидкости устанавливаются на одном уровне
3) поверхности разных жидкостей устанавливаются в них на одном уровне
2 вариант
1. На земле лежат: доска (№1), обрубок бревна (№2), ведро с водой (№3), ящик с песком (№4), имеющие одинаковые массы. Какое из этих тел оказывает наибольшее давление на землю?
1) №1
2) №2
3) №3
4) №4
2. По какой формуле рассчитывают давление твёрдого тела?
1) р = gρh
2) Р = gm
3) p = F/S
4) ρ = m/V
3. Какая единица служит для измерения давления и чему она равна?
1) Специальной единицы давления нет
2) Ньютон, 1 Н
3) Килограмм, 1 кг
4) Паскаль, 1 Н/м2
4. Выразите давления, равные 200 Н/м2 и 8 кПа, в паскалях.
1) 20 Па, 800 Па
2) 200 Па, 8000 Па
3) 2000 Па, 8000 Па
4) 2000 Па, 80 000 Па
5. У бидона с молоком, вес которого 480 Н, дно имеет площадь 0,12 м2. Какое давление оказывает он на землю?
1) 4000 Па
2) 400 Па
3) 40 Па
4) 0,4 кПа
6. Определите давление на стол стопки книг общей массой 1,5 кг, площадь соприкосновения которых с ним 300 см2.
1) 5 кПа
2) 500 Па
3) 50 Па
4) 5 Па
7. Одинаковое количество кислорода и углекислого газа находится в сосудах одинакового объема при одной и той же температуре. Одинаковы ли давления этих газов?
1) Одинаковы
2) Давление кислорода больше
3) Давление углекислого газа больше
8. Как следует поступить с баллоном, наполненным газом, чтобы его давление не изменилось?
1) Убрать в холодное помещение
2) Оставить в тени
3) Положить на солнце
4) Давление изменится в любом случае
9. Жидкость, находящуюся в сосуде, сжимают поршнем, который создаёт давление 5 кПа. Какое добавочное давление будет действовать при этом на площадки №1, №2, №3?
1) №1 – 1 кПа
2) №2 – 0 Па
3) №3 – 10 кПа
4) Добавочное давление на все площадки будет одинаковым и равным 5 кПа
10. Давление жидкости вычисляют по формуле
1) ρ = m/V
2) F = kΔl
3) p = gρh
4) p = F/S
11. Каково давление воды на глубине 2 м?
1) 20 кПа
2) 10 кПа
3) 200 кПа
4) 100 кПа
12. На расстоянии 10 см от дна сосуда с водой находится площадка. Найдите давление воды на неё.
1) 100 Па
2) 1000 Па
3) 300 Па
4) 3000 Па
13. Сколько воды надо налить в сосуды №2 и №3, чтобы давление на дно в каждом из них было таким же, как давление воды в сосуде №1?
1) Нельзя определить из-за недостатка данных
2) Доверху
3) До уровня, на котором находится поверхность воды в сосуде №1
4) Давление в любом случае будет разным, поскольку размеры дна в сосудах не одинаковы
14. В сосуды налиты до одной и той же высоты разные жидкости: ацетон (№1), бензин (№2), керосин (№3). В каком из сосудов давление на дно наименьшее?
1) №1
2) №2
3) №3
4) Во всех одинаково
15. В каком из сообщающихся сосудов находится однородная жидкость?
1) №1
2) №2
3) №3
4) Ни в каком
Ответы на тест по темам Давление, Давление в жидкости и газе, Сообщающиеся сосуды
1 вариант
1-2
2-4
3-3
4-1
5-1
6-3
7-3
8-3
9-4
10-1
11-2
12-1
13-4
14-1
15-2
2 вариант
1-3
2-3
3-4
4-2
5-1
6-2
7-1
8-2
9-4
10-3
11-1
12-4
13-3
14-2
15-2
Источник
