В теплоизолированном длинном цилиндрическом сосуде

1. Воздушный шар объемом 2500 м3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. До какой минимальной температуры нужно нагреть воздух в шаре, чтобы шар взлетел вместе с грузом (корзиной и воздухоплавателем) массой 200 кг? Температура окружающего воздуха 7°С, его плотность 1,2 кг/м3. Оболочку шара считать нерастяжимой. (Решение)

2. Воздушный шар объемом 2500 м3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Рассчитайте максимальную массу груза, который может поднять шар, если воздух в нем нагреть до температуры 77°С. Температура окружающего воздуха 7°С, его плотность 1,2 кг/м3. Оболочку шара считать нерастяжимой. (Решение)

3.
Воздушный шар объемом 2500 м3 имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Если температура окружающего воздуха 7°С, а его плотность 1,2 кг/м3, то при нагревании воздуха в шаре до температуры 77°С шар поднимает груз с максимальной массой 200 кг. Какова масса оболочки шара? Оболочку шара считать нерастяжимой. (Решение)

4.
Воздушный шар имеет газонепроницаемую оболочку массой 400 кг и содержит 100 кг гелия. Какой груз он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па? Считать, что оболочка шара не оказывает сопротивления изменению объема шара. (Решение)

5.
Воздушный шар с газонепроницаемой оболочкой массой 400 кг заполнен гелием. Он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па, груз массой 225 кг. Какова масса гелия в оболочке шара? Считать, что оболочка шара не оказывает сопротивления изменению объема шара. (Решение)

6. При исследовании уравнения состояния газа ученик соединил сосуд (1) объемом 150 мл с манометром (2) тонкой трубкой и опустил сосуд в горячую воду (см. рисунок). Чему равна плотность воздуха в сосуде? Начальные показания манометра равны 0 мм рт. ст. Шкала манометра и нижняя шкала барометра (3) проградуированы в мм рт. ст. Верхняя шкала барометра проградуирована в кПа. Объем измерительного механизма манометра и соединительной трубки значительно меньше 150 мл. (Решение)

7. Теплоизолированный сосуд объемом V = 2 м3 разделен пористой неподвижной перегородкой на две равные части. Атомы гелия могут свободно проникать через поры в перегородке, а атомы аргона — нет. В начальный момент в одной части сосуда находится νHe = 2 моль гелия, а в другой — νAr = 1 моль аргона. Температура гелия TНe = 300 К, а температура аргона ТAr = 600 К. Определите температуру гелия после установления равновесия в системе. (Решение)

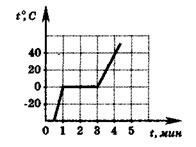8. На рисунке представлен график изменения температуры вещества в калориметре с течением времени. Теплоемкостью калориметра и тепловыми потерями можно пренебречь и считать, что подводимая к сосуду мощность постоянна. Рассчитайте удельную теплоемкость вещества в жидком состоянии. Удельная теплота плавления вещества равна 100 кДж/кг. В начальный момент времени вещество находилось в твердом состоянии. (Решение)

9. В цилиндрическом сосуде под поршнем длительное время находятся вода
и ее пар. Поршень начинают вдвигать в сосуд. При этом температура
воды и пара остается неизменной. Как будет меняться при этом масса
пара в сосуде? Ответ поясните.
(Решение)

10. В цилиндрическом сосуде под поршнем длительное время находятся вода
и ее пар. Поршень начинают вдвигать в сосуд. При этом температура
воды и пара остается неизменной. Как будет меняться при этом
отношение массы пара к массе жидкости в сосуде? Ответ поясните. (Решение)

11. В цилиндр объемом 0,5 м3 насосом закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии стержнем, который может свободно поворачиваться вокруг оси в точке А (см. рисунок). К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через 580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Площадь закрытого клапаном отверстия 5·10-4 м2, расстояние АВ равно 0,1 м. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите длину стержня, если его можно считать невесомым.
(Решение)

12. В цилиндр объемом 0,5 м3 насосом закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии стержнем, который может свободно поворачиваться вокруг оси в точке А (см. рисунок к зад. 11). К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через 580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Площадь закрытого клапаном отверстия 5·10-4 м2, расстояние АВ равно 0,1 м. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите длину AB. (Решение)

13. Воздушный шар имеет газонепроницаемую оболочку массой 400 кг и содержит 100 кг гелия. Какой груз он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па? Считать, что оболочка шара не оказывает сопротивления изменению объема шара.
(Решение)

14. Воздушный шар, оболочка которого имеет массу М = 145 кг и объем V = 230 м3, наполняется горячим воздухом при нормальном атмосферном давлении и температуре окружающего воздуха t0 = 0°C. Какую минимальную температуру t должен иметь воздух внутри оболочки, чтобы шар начал подниматься? Оболочка шара нерастяжима и имеет в нижней части небольшое отверстие.

(Решение)

15. В высоком вертикальном цилиндрическом сосуде под тяжелым поршнем, способным перемещаться вдоль стенок сосуда практически без трения, находится некоторое количество воздуха под давлением p = 1,5 атм. Поршень находится в равновесии на высоте H1 = 20 см над дном сосуда. Определите, на какое расстояние ΔH сместится поршень, если сосуд перевернуть открытым концом вниз и дождаться установления равновесия. Считать температуру воздуха и атмосферное давление p0 = 1 атм постоянными. Массой воздуха в сосуде по сравнению с массой поршня можно пренебречь.
(Решение)

16. Горизонтальный хорошо теплопроводящий цилиндр, разделённый подвижными поршнями площадью S = 100 см2 на 5 отсеков (№№ 1—5), содержит в них одинаковые количества идеального газа при температуре окружающей среды и под давлениями, равными давлению pа = 105 Па окружающей цилиндр атмосферы (см. рисунок). Каждый поршень сдвигается с места, если приложенная к нему горизонтальная сила превышает силу сухого трения Fтр = 2 Н. К самому левому поршню прикладывают горизонтальную силу F, медленно увеличивая её по модулю. Какого значения достигнет F, когда объём газа в самом правом, 5-м отсеке цилиндра уменьшится в n = 2 раза? Процессы изменения состояния газов в отсеках цилиндра считать изотермическими.
(Решение)

17. Горизонтальный хорошо теплопроводящий цилиндр, разделённый подвижными поршнями площадью S = 50 см2 на 5 отсеков (№№ 1—5), содержит в них одинаковые количества идеального газа при температуре окружающей среды и под давлениями, равными давлению pа = 105 Па окружающей цилиндр атмосферы (см. рисунок к зад 16). Каждый поршень сдвигается с места, если приложенная к нему горизонтальная сила превышает силу сухого трения Fтр = 4 Н. К самому левому поршню прикладывают горизонтальную силу F, медленно увеличивая её по модулю. Когда давление газа в самом правом, пятом отсеке цилиндра, увеличится в n = 3 раза? Процессы изменения состояния газов в отсеках цилиндра считать изотермическими.
(Решение)

18. Газ в цилиндрическом сосуде разделен на две равные части подвижным поршнем, имеющим массу m и площадь сечения S. При горизонтальном положении цилиндра давление газа в каждой половине сосуда равно p. Определить давление p1 газа над поршнем при вертикальном положении цилиндра. Температуру газа считать постоянной.
(Решение)

19. Сферическую оболочку воздушного шара делают из материала, квадратный метр которого имеет массу 1 кг. Шар наполняют гелием при атмосферном давлении 105 Па. Определите минимальную массу оболочки, при которой шар начнет поднимать сам себя. Температура гелия и окружающего воздуха одинакова и равна 0°С. (Площадь сферы S= 4πr2, объем шара V = 4/3πr3.)

(Решение)

20. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Площадь поперечного сечения поршня S = 30 см2. Давление окружающего воздуха p = 105 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. Какое количество теплоты нужно отвести от газа при его медленном охлаждении, чтобы поршень передвинулся на расстояние х = 10 см?
(Решение)

21. В горизонтальном цилиндрическом сосуде, закрытом подвижным поршнем, находится одноатомный идеальный газ. Давление окружающего воздуха р = 105 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. В процессе медленного охлаждения от газа отведено количество теплоты |Q| = 75 Дж. При этом поршень передвинулся на расстояние х = 10 см. Чему равна площадь поперечного сечения поршня?
(Решение)

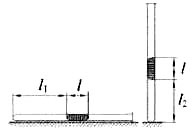22. В запаянной с одного конца длинной горизонтальной стеклянной трубке постоянного сечения (см. рисунок) находится столбик воздуха длиной l1 = 30,7 см, запертый столбиком ртути. Если трубку поставить вертикально отверстием вверх, то длина воздушного столбика под ртутью будет равна l2 = 23.8 см. Какова длина ртутного столбика? Атмосферное давление 747 мм рт. ст.
(Решение)

23. В водонепроницаемым мешок, лежащий на дне моря на глубине 73,1 м. закачивается сверху воздух. Вода вытесняется из мешка через нижнее отверстие, и. когда объём воздуха в мешке достигает 28,0 м, мешок всплывает вместе с прикреплённым к нему грузом массой 25,0 тонн. Определите массу воздуха в мешке в момент начала его всплывания. Температура воды раина 7°С. атмосферное давление па уровне моря равно 105 Па. Объёмом груза и стенок мешка пренебречь. Масса оболочки мешка неизвестна.
(Решение)

24. Сосуд разделен тонкой перегородкой на две части, отношение объёмов у которых V2/V1 = 3. В первой и второй частях сосуда находится воздух с относительной влажностью соответственно φ1 = 60% и φ2 = 70%. Какой будет влажность воздуха в сосуде, если перегородку убрать? Считать, что температура воздуха постоянна.(Решение)

25. В металлическом сосуде под поршнем находится воздух при атмосферном давлении (см. рисунок). Сосуд имеет массу 10 кг и расположен в горизонтальном положении на поверхности стола. Поршень может скользить без трения со стенками сосуда. Массон поршня и воздуха, заключённого в сосуде, можно пренебречь. За привязанный к нему шнур поршень очень медленно тянут в горизонтальном направлении. На сколько процентов возрастёт объём воздуха под поршнем к моменту, когда сосуд начнёт скользить по столу? Коэффициент трения покоя между сосудом и поверхностью стола равен 0,5. Площадь дна поршня 105 см2. Атмосферное давление 105 Па.
(Решение)

26.Один моль одноатомного идеального газа совершает процесс 1-2-3, график которого показан на рисунке в координатах р-Т. Известно, что давление газа р в процессе 1-2 увеличилось в 2 раза. Какое количество теплоты было сообщено газу в процессе 1-2-3, если его температура Т в состоянии 1 равна 300 К, а в состоянии 3 равна 900 К?
(Решение)

27. Теплоизолированный цилиндр разделён подвижным теплопроводящим поршнем на две части. В одной части цилиндра находится гелий, а в другой – аргон. В начальный момент температура гелия равна 300 К,. а аргона – 900 К. Объёмы, занимаемые газами, одинаковы, а поршень находится в равновесии. Во сколько раз изменится объём, занимаемый гелием, после установления теплового равновесия, если поршень перемешается без трения? Теплоёмкостью цилиндра н поршня пренебречь.
(Решение)

Окончательно с.

Задача 2. Метеорологическая ракета. Метеорологическая ракета стартует в вертикальном направлении с по­верхности Земли. Ее топливо сгорает за τ = 40 с полета. В течение этого времени ускорение ракеты возрастает линейно от а0 = g до аτ = 5g. Найдите мощность двигателя ракеты перед окончанием его работы. Масса не заправ­ленной ракеты m0 = 10 кг, ускорение свободного падения g = 10 м/с2.

Возможное решение

Ускорение ракеты а(t) = а0 + (аτ – а0).

По аналогии с тем, что пройденному пути соот­ветствует площадь под графиком скорости, нахо­дим скорость Vτ ракеты в момент τ как площадь под графиком ускорения (рис.13): Vτ= τ ( аτ + а0)/2.

Согласно второму закону Ньютона, m аτ =F–mg, где F — сила тяги в конце полета. Мощность двигателя в этот момент

N = F Vτ = ( аτ + g) ( аτ + а0) = 720 кВт.

Задача 3. Тяжелый поршень. В теплоизолированном цилиндрическом сосуде с вертикаль­ными гладкими стенками на небольших опорах лежит тяже­лый однородный поршень толщиной h и плотностью ρ (рис. 14). Под поршнем находится газ массой m c удельной теплоемко­стью C. Первоначально давление газа внутри цилиндра равно атмосферному. Газ начинают нагревать, при этом увеличение его давления Δp = α mΔt, где α – заданная константа, Δt – изменение температуры. Какое минимальное количество Q подвести к газу, чтобы поршень сдвинулся с места?

Возможное решение

Пусть М — масса поршня, S — площадь его основания, тогда чтобы он сдвинулся с места, давление газа в цилиндре должно превысить атмосферное на величину

.

Из связи Δр и Δt находим . Следовательно, Q=cmΔt = .

Задача 4. Сосуд на опорах Легкий цилиндрический сосуд с жидкостью плотностью ρ0 стоит на двух параллельных опорах, силы реакций ко­торых составляют N1 и N2 (рис. 15). В сосуд опустили на нити шарик массой m и плотностью ρ так, что он оказался на одной вертикали со второй опорой. При этом шарик пол­ностью погружен в воду и не касается сосуда. Определите новые силы N‘1 и N‘2 реакций опор.

Возможное решение

Пусть F и F’ — силы давления жидкости на основание сосуда до и после погружения шарика, тогда F’ =F +.

Поскольку сосуд легкий и цилиндрический, то при увеличении уровня воды центр масс сосуда с водой не смещается по горизонтали. Следовательно, точ­ки приложения сил F и F‘ совпадают. Запишем условия равновесия сосуда до и после погружения шарика:

N1+N2= F, N‘1+N‘2= F‘, N1l1 = N2l2, N‘1l1 = N‘2l2, где l1 и l2 — плечи реакций опор относительно точки приложения силы F.

Откуда N‘1 = N1, N‘2 = N2.

Заметим, что ответ не зависит от места погружения шарика.

Задача 5. Измерения в электрической цепи. Семь резисторов сопротивлениями R1=1кОм, R2=2кОм, R3=0,5кОм, R4=2,5кОм, R5=2кОм, R6=1кОм, R7=1кОм соединены с источни­ком постоянного напряжения U=30 В (рис.16). К резисторам подключили два вольтметра и два амперметра. Определите их показания V1, V2, I1, I2. Приборы считайте идеальными.

Возможное решение

Перерисуем схему без вольтметров (рис. 17). Сопротивление каждой из параллельных ветвей цепи составляет r = R1 + R2 = R3 + R4= R5 + R6 = 3 кОм, поэтому полное сопротивление цепи

кОм.

Через резистор R7 сила тока I = U/R. Через каждую из параллельных ветвей цепи течет одинаковый ток, поэтому сила тока в каждой из них i = I/3, откуда

I1= I2=2i=2U/3R=10 мА.

Показания V1 и V2 вольтметров найдем как напряжения между соответству­ющими точками: В, В.

10 класс

Задача 1. Клин и шайба (1). Вблизи вершины клина массой М, высотой Н и с длиной основания L удерживают небольшую шай­бу массой m (рис. 18). Клин покоится на гладкой го­ризонтальной поверхности. Шайбу отпускают и она соскальзывает к основанию клина. На какое рассто­яние S при этом переместится клин?

Возможное решение

Поскольку внешние силы, действующие на систему «клин-шайба», не име­ют горизонтальных составляющих, горизонтальная координата центра масс системы не меняется: m(L – S) – MS = 0, откуда S = .

Задача 2. Клин и шайба (2). При выполнении условий предыдущей задачи най­дите максимальную скорость V клина. Трением меж­ду клином и шайбой пренебречь.

Возможное решение

Скорость клина будет максимальной, когда шайба достигнет его основания. Пусть – ско­рость шайбы в этот момент относительно кли­на, а – ее скорость в неподвижной системе отсчета (рис. 22). По теореме косину­сов для треугольника скоростей:

v2 = u2 + V2 – 2uVcos a. (1)

Поскольку внешние силы, действующие на систему «клин-шайба» вертикальны, проекция импульса системы на ось х не меняется: О = m(u cos a – V) – MV, откуда

(2).

По закону сохранения энергии: mgH =

Подставив (1) и (2) в последнее уравнение и учитывая, что cos а = , найдем .

Задача 3. Стакан-поплавок. В глубоком цилиндрическом сосуде с внутренним диаметром D находится вода, в которой дном вниз плавает тонкостенный металлический стакан мас­сой m и высотой H. Благодаря направляющим стенки стакана и цилиндра остаются параллельными. Какую минимальную работу А нужно совершить, чтобы утопить этот стакан, то есть заставить его пойти ко дну? Известно, что утопленный стакан не всплывает, а максимальная масса вмещаемой им воды равна М.

Возможное решение

Будем медленно опускать стакан в воду. Для этого к нему нужно прикла­дывать вертикально вниз силу F, уравновешивающую сумму силы Архимеда и силы тяжести, действующие на стакан. Пока в стакане нет воды, F линейно зависит от глубины погружения х, причем F(0) = 0.

Край стакана сравняется с уровнем жидкости в сосуде при х = х1, (рис. 20). При этом

F(x1) = Мg – mg = F.