В теплоизолированном сосуде при температуре

В кастрюлю-скороварку налили немного воды. закрыли герметично и поставили на огонь. К тому моменту, когда вся вода испарилась, температура кастрюли оказалась $115^{ circ} С$, а давление внутри – 3 атмосферы. Какую часть объема вначале занимала вода? Начальная температура $20^{ circ} С$.

Подробнее

Тонкая квадратная пластинка АБВГ сделана из меди. Ее нагревают со стороны торца АБ, поддерживая его температуру равной $100^{ circ} С$, и охлаждают со стороны трех остальных торцов, поддерживая их температуру равной $0^{ circ} С$. Найдите температуру в центре пластинки.

Подробнее

Внутри длинной трубы, наполненной воздухом, двигают с постоянной скоростью поршень, при этом в трубе распространяется со скоростью 320 м/с упругая волна. Считая перепад давлений на границе распространения волны равным 1000 Па, оцените перепад температур. Давление в невозмущенном воздухе 1 атм, температура 300 К.

Подробнее

Внутри большого мыльного пузыря находится маленький, радиус которого в 10 раз меньше. Воздух снаружи откачивают, после чего радиус большого пузыря увеличивается в 2 раза. Во сколько раз увеличится радиус внутреннего пузыря? Температуру считайте постоянной, влиянием силы тяжести можно пренебречь.

Подробнее

В теплоизолированном цилиндрическом сосуде под поршнем находится сильно разреженный гелий при температуре $T_{0} = 100 К$. Поршень очень медленно отодвигают на некоторое расстояние, после чего в сосуде устанавливается температура $T_{1} = 99 К$. Какая температура установится в сосуде, если поршень передвинуть очень быстро? Что такое “очень быстро” в этом случае? Сделайте оценку такой скорости передвижения поршня, при которой изменение температуры составит $Delta T = 0,5 К$.

Подробнее

В цилиндрическом сосуде под тяжелым поршнем находится кислород (рис.). Поршень поднимают на высоту $h$ от положения равновесия, дожидаются установления температуры, затем сосуд теплоизолируют и поршень отпускают. На каком расстоянии от прежнего положения равновесия установится поршень, когда система вновь придет в равновесие? Теплоемкостью стенок и поршня пренебречь.

Подробнее

Один из спаев термопары находится в комнате при температуре $t_{1} = 27^{ circ} С$, а второй – в теплоизолированном сосуде со льдом, имеющим температуру $t_{2} = 0^{ circ} C$ (см. рисунок). Мощность, развиваемая термопарой, выделяется на сопротивлении нагревателя, который помещен в другой теплоизолированный сосуд, содержащий воду. Оцените, на сколько повысится температура воды к моменту окончания плавления льда. Считайте, что все сопротивление цепи сосредоточено в нагревателе. Массы воды и льда одинаковы. Удельная теплоемкость воды $c = – 4,2 кДж/(кг cdot К)$, удельная теплота плавления льда $lambda = 335 кДж/кг$.

Подробнее

Два сосуда объемом $V = 0,5 л$ каждый соединены вертикальной стеклянной трубкой сечением $S = 1 см^{2}$ (рас.). Трубка перекрыта подвижным поршнем – магнитом массой $m = 2,0 г$, который может двигаться вдоль трубки без трения. При помощи катушек, подключенных к генератору переменною напряжения, возбуждают колебания поршня вдоль трубки. На рисунке приведена экспериментально полученная зависимость амплитуды установившихся колебаний поршня от частоты приложенного переменного напряжения. Определите по этим данным отношение молярных теплоемкостей $C_{p}/C_{V}$ для воздуха. В первом опыте вентиль наверху был закрыт. При какой частоте наступит максимум при открытом вентиле? Оцените амплитуду колебаний поршня в этом случае на частоте $f_{0}$. Давление воздуха $p_{0} = 1 атм.

Подробнее

Пленка при температуре $t_{1}= + 50^{ circ} С$ имеет коэффициент поверхностного натяжения $sigma_{1} = 0,020 Н/м$. После увеличения температуры до $t_{2} = +51^{ circ} С$ коэффициент поверхностного натяжения падает до $sigma_{2} = 0,0195 Н/м$. Будем медленно растягивать пленку так, чтобы ее температура оставалась постоянной. Поглощает пленка при этом тепло из окружающей среды или, наоборот, отдает его? Оцените количественно этот теплообмен при растяжении пленки от $S_{1} = 1 м^{2}$ до $S_{2} = 1,5 м^{2}$ при температуре $+ 50^{ circ} C$.

Указание. Подумайте, как применить тут формулу для КПД цикла Карно.

Подробнее

Возьмем короткую трубочку небольшого диаметра $D$ и выдуем мыльный пузырь радиусом $R_{0} gg D$. Откроем теперь конец трубочки и подождем, пока пузырь сдуется. Оцените время жизни такого пузыря от начала сдувания, если $D = 2 мм, R_{0} = 2 см$. Коэффициент поверхностного натяжения воды $sigma = 0,07 Н/м$.

Подробнее

В насыщенные пары воды при температуре $t = 100^{ circ} С$ поместили металлическую пластину, охлажденную до температуры жидкого азота. Оцените начальную скорость роста толщины слоя намерзающего льда.

Подробнее

В объеме $V_{0}$ при температуре $T_{0}$ и давлении $p$ находился воздух, содержащий некоторое количество озона $O_{3}$. После долгого выдерживания в тени озон полностью превратился в молекулярный кислород. При том же давлении температура воздуха стала $T$, объем – $V$. Найдите начальное число молей озона.

Подробнее

Сосуд объемом $V = 10 л$ с площадью поперечного сечения $S = 0,01 м^{2}$ разделен пополам тяжелым поршнем массой $m = 1 кг$, который может двигаться без трения. В каждой половине сосуда содержится $m = 5 г$ воды, а воздух откачан. Температура сосуда и его содержимом поддерживается равной $T = 350 К$. Поршень сдвигают от середины на расстояние $d = 1 см$ и отпускают. Как будет двигаться поршень? Как зависит характер движения поршня от температуры сосуда?

Подробнее

В сосуде под поршнем находится некоторое количество азота. Медленно отодвигая поршень, плавно уменьшим давление газа. Какова молярная теплоемкость газа на малом участке процесса, если при увеличении объема па 1% давление уменьшилось на 0,5%?

Подробнее

Газовая смесь состоит из равного числа молей гелия, азота и углекислого газа. Найдите показатель адиабаты для такого газа.

Подробнее

Задачи на количество теплоты с решениями

Формулы, используемые на уроках «Задачи на количество теплоты,
удельную теплоемкость».

1 г = 0,001 кг;     1 т = 1000 кг;    1 кДж = 1000 Дж;    1 МДж = 1000000 Дж

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
 В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?

При решении задачи нужно учесть, что оба тела — и котёл, и вода — будут нагреваться вместе. Между ними происходит теплообмен. Их температуры можно считать одинаковыми, т. е. температура котла и воды изменяется на 100 °С — 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми. Ведь их массы и удельные теплоёмкости различны.

Задача № 2.
 Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.

Задача № 3.
 Стальная деталь массой 3 кг нагрелась от 25 до 45 °С. Какое количество теплоты было израсходовано?

Задача № 4.
 В сосуде содержится 3 л воды при температуре 20 °С. Сколько воды при температуре 45 °С надо добавить в сосуд, чтобы в нём установилась температура 30 °С? Необходимый свободный объём в сосуде имеется. Теплообменом с окружающей средой пренебречь

Задача № 5.
 На сколько градусов изменилась температура чугунной детали массой 12 кг, если при остывании она отдала 648000 Дж теплоты?

Задача № 6.
 По графику определите удельную теплоёмкость образца, если его масса 50 г.

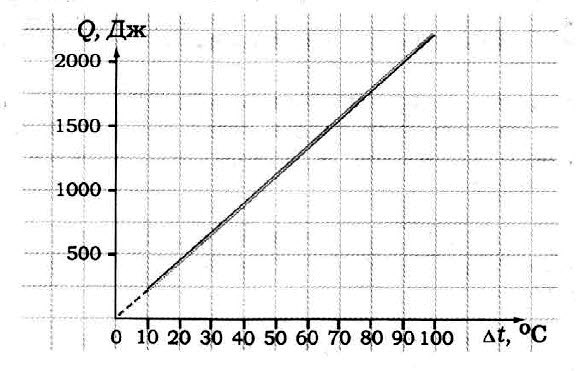
Задача № 7.
 Для нагревания медного бруска массой 3 кг от 20 до 30 °С потребовалось 12000 Дж теплоты. Какова удельная теплоемкость меди?

Задача № 8.
 Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей 2,1 кДж энергии. Чему равна удельная теплоемкость камня?

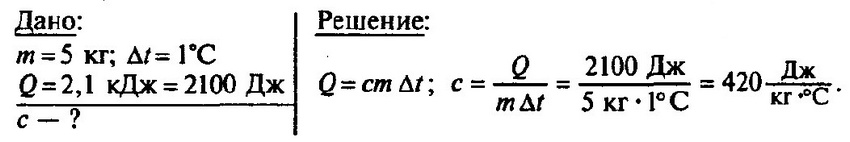
Задача № 9.
 Какое количество теплоты потребуется для нагревания на 1 °С воды объемом 0,5 л; олова массой 500 г; серебра объемом 2 см3; стали объемом 0,5 м3; латуни массой 0,2 т?

Задача № 10.
 Какое количество теплоты получили алюминиевая кастрюля массой 200 г и находящаяся в ней вода объемом 1,5 л при нагревании от 20 °С до кипения при температуре 100 °С?

Задача № 11.
 а) Воздух, заполняющий объем 0,5 л в цилиндре с легким поршнем, нагрели от 0 до 30 °С при постоянном атмосферном давлении. Какое количество теплоты получил воздух? 
б) В порожнем закрытом металлическом баке вместимостью 60 м3 под действием солнечного излучения воздух нагрелся от 0 до 20 °С. Как и на сколько изменилась внутренняя энергия воздуха в баке? (Удельная теплоемкость воздуха при постоянном объеме равна 720 Дж/кг-°С.)

Задача № 12.
  ОГЭ
 Металлический цилиндр массой m = 60 г нагрели в кипятке до температуры t = 100 °С и опустили в воду, масса которой mв = 300 г, а температура tв = 24 °С. Температура воды и цилиндра стала равной Θ = 27 °С. Найти удельную теплоёмкость металла, из которого изготовлен цилиндр. Удельная теплоёмкость воды св = 4200 Дж/(кг К).

Задача № 13.
 В теплоизолированном сосуде сначала смешивают три порции воды 100 г, 200 г и 300 г с начальными температурами 20 °C, 70 °C и 50 °C соответственно. После установления теплового равновесия в сосуд добавляют новую порцию воды массой 400 г при температуре 20 °C. Определите конечную температуру в сосуде. Ответ дайте в °C, округлив до целого числа. Теплоёмкостью калориметра пренебрегите.

Решение.

Ответ: 39 °С.

Задача № 14. (повышенной сложности)
 Стальной шарик радиусом 5 см, нагретый до температуры 500 ˚С, положили на лед, температура которого 0 ˚С. На какую глубину погрузится шарик в лед? (Считать, что шарик погрузился в лед полностью. Теплопроводностью шарика и нагреванием воды пренебречь.)

Дано: R = 0,05 м;   t1 = 500 ˚С;   t2 = 0 ˚С;
ρ1 (плотность стали) = 7800 кг/м3.;
ρ2 (плотность льда) = 900 кг/м3.
c (удельная теплоемкость стали) = 460 Дж/кг •˚С,
λ (удельная теплота плавления льда) = 3,3 • 105 Дж/кг,

Найти: h – ?

Краткая теория для решения Задачи на количество теплоты.

Конспект урока «Задачи на количество теплоты».

Посмотреть конспект урока по теме «Количество теплоты. Удельная теплоемкость»

Следующая тема: «ЗАДАЧИ на сгорание топлива с решениями».