В теплоизолированном сосуде теплоемкость которого

Страницы: 1 … 3 4 [5] 6 7
Автор Тема: Репетиционное тестирование 2 этап 2013/2014 (Прочитано 16772 раз)
0 Пользователей и 1 Гость просматривают эту тему.
А3 вариант 1 Угол поворота φ колеса вокруг неподвижной оси, совпадающей с его осью вращения, изменяется в зависимости от времени t по закону φ(t) = А·t, где А = 3 рад/с. Если радиус колеса R = 20 см, то модуль линейной скорости υ точки, лежащей на его ободе, равен:
1) 0,30 м/с; 2)0,60 м/с; 3) 3 м/с; 4) 6 м/с; 5) 9 м/с
Решение. Угловая скорость определяется как величина, численно равная углу поворота радиус-вектора за единицу времени:
[ omega =frac{varphi }{t};,,,varphi =omega cdot t ]
Легко видеть, что ω = А. Линейная и угловая скорости связаны следующим соотношением:
υ = ω·R
Ответ: 2)0,60 м/с
Записан
А4 вариант 2 Отношение расстояния l от поверхности Земли до точки, в которой ускорение свободного падения в четыре раз меньше, чем у ее поверхности к радиусу R Земли равно:
1) 1; 2) 2; 3) 3; 4) 4; 5) 5.
Решение. Смотри решение А4 вариант 2
[ ,l=Rcdot left( sqrt{frac{g}{{{g}_{1}}}}-1 right)=R;,,,,frac{l}{R}=1 ]
Ответ: 1) 1;
Записан
А6 вариант 1 На рисунке показаны графики (1 и 2) зависимости гидростатического давления р от глубины h для двух различных жидкостей. Если плотность первой жидкости ρ1 = 0,80 г/см3, то плотность ρ2 второй жидкости равна:
1) 0,80 г/см3; 2) 0,90 г/см3; 3) 1,5 г/см3; 4) 1,6 г/см3; 5) 1,8 г/см3.
Решение. Как видно из графика, для первой жидкости h = 25 cм, р1 = р0. Для второй жидкости – h = 25 cм, р2 = 2·р0. Тогда
р1 = p0 = ρ1·g·h; р2 = 2·p0 = ρ2·g·h
Решим уравнения, например разделим первое уравнение на второе
ρ2 = 2·ρ1
Ответ: 4) 1,6 г/см3;
Записан
А7 вариант 1 Соотношение между количеством теплоты Q, отдаваемым идеальным одноатомным газом, и работой А’, совершаемой внешними силами при его изотермическом сжатии, обозначено цифрой:
1) 1; 2) 2; 3) 3; 4) 4; 5) 5
[ 1),Q=frac{3}{2}{{A}^{‘}};,,2),Q={{A}^{‘}};,,,,3),Q=0;,,,4),Q=frac{5}{2}{{A}^{‘}};,,5),Q=frac{2}{5}{{A}^{‘}} ]
Решение. Для изотермического процесса T – const, ΔТ = 0, следовательно, ΔU = 0. Над газом совершается работа А’, внутренняя энергия не изменяется, значит тепло выделяется Q<0. Тогда первый закон термодинамики запишется так
0 = -Q + А’; Q = А’
Ответ: 2) 2;
Записан
А8 вариант 1 Если в результате изотермического расширения давление идеального газа уменьшилась на Δр = 40 кПа, а его объем увеличился в k = 5,0 раза, то давление р2 газа в конечном состоянии равно:
1) 8,0 кПа; 2) 10 кПа; 3) 18 кПа; 4) 20 кПа; 5) 35 кПа;
Решение. Для изотермического процесса выполняется закон Бойля-Мариота:
p1·V1=p2·V2; p1 = Δp+p2; V2 = k·V1
[ left( Delta p+{{p}_{2}} right)cdot {{V}_{1}}={{p}_{2}}cdot kcdot {{V}_{1}};,,,,,,{{p}_{2}}=frac{Delta p}{k-1} ]
Ответ: 2) 10 кПа;
Записан
В5. Вариант 1.
В баллон, содержащий m1 = 50 г неона (M1 = 20 г/моль) добавили m2 = 56 г азота (M2 = 28 г/моль). Если температура газа в баллоне не изменилась, то относительное изменение давления газа Δp/p∙100 % в баллоне равно …%.
Решение: пусть объём сосуда V, температура газа T. Первоначальное давление в сосуде p1 – это давление неона. Конечное давление p/ равно давлению смеси газов p/ = p1+ p2. Запишем уравнение Клапейрона – Менделеева для данных газов
[ begin{array}{l} {p_{1} cdot V=frac{m_{1} }{M_{1} } cdot Rcdot T,} \ {p_{2} cdot V=frac{m_{2}}{M_{2}} cdot Rcdot T,} \ {p’cdot V=left(frac{m_{1} }{M_{1} } +frac{m_{2}}{M_{2}} right)cdot Rcdot T.} end{array} ]
Относительное изменение давления
[ begin{array}{l} {frac{Delta p}{p} cdot 100% =frac{p’-p_{1} }{p_{1} } cdot 100% ,} \ {frac{Delta p}{p} cdot 100% =frac{left(frac{m_{1} }{M_{1}} +frac{m_{2} }{M_{2}} right)cdot frac{Rcdot T}{V} -frac{m_{1}}{M_{1} } frac{Rcdot T}{V} }{frac{m_{1} }{M_{1} } frac{Rcdot T}{V}} ,} \ {frac{Delta p}{p} cdot 100% =frac{m_{2} cdot M_{1}}{m_{1} cdot M_{2}} cdot 100%.} end{array} ]
Ответ: 80%.
Записан
В6. Вариант 2.
В теплоизолированный сосуд, теплоёмкостью которого можно пренебречь, содержащий воду (с = 4,2 кДж/(кг∙ºС)) массой m1 при температуре t1 = 25,0 ºС, впустили водяной пар (L = 2,26 МДж/кг) массой m2 = 37 г при температуре t2 = 100ºС. Если после установления теплового равновесия температура воды в сосуде стала t3 = 65ºС, то начальная масса m1 воды в сосуде была равна …г.
Решение: происходит теплообмен. При этом водяной пар конденсируется (он находится при температуре 100ºС) и получившаяся из него вода остывает. Количество теплоты, выделившееся при конденсации пара и остывании воды, будет равно
[ Q_{1} =-Lcdot m_{2} +ccdot m_{2} cdot left(t_{3} -t_{2} right). ]
Вода в сосуде будет нагреваться, получив при этом количество теплоты
[ Q_{2} =ccdot m_{1} cdot left(t_{3} -t_{1} right). ]
Запишем уравнение теплового баланса
[ begin{array}{l} {Q_{1} +Q_{2} =0,{rm ; ; ; ; ; ; ; }-Lcdot m_{2} +ccdot m_{2} cdot left(t_{3} -t_{2} right)+ccdot m_{1} cdot left(t_{3} -t_{1} right)=0,} \ {ccdot m_{1} cdot left(t_{1} -t_{3} right)=-Lcdot m_{2} +ccdot m_{2} cdot left(t_{3} -t_{2} right),} \ {m_{1} =frac{-Lcdot m_{2} +ccdot m_{2} cdot left(t_{3} -t_{2} right)}{ccdot left(t_{1} -t_{3} right)}.} end{array} ]
Ответ: 530 г.
Записан
В8. Вариант 1.
Две когерентные электромагнитные волны частотой ν = 2 ∙ 1014 Гц, распространяющиеся в однородной среде, образуют интерференционный максимум седьмого порядка (m = 7). Если абсолютный показатель преломления среды n = 1,5, то геометрическая разность хода δ этих волн равна …мкм.
Решение: условие максимума интерференции – разность хода равна чётному числу полуволн
[ delta =2mcdot frac{lambda}{2}, ]
здесь λ – длина волны в однородной среде с показателем преломления n.
[ lambda =frac{upsilon }{nu } ,{rm ; ; ; }n=frac{c}{upsilon } ,{rm ; ; ; }lambda =frac{c}{ncdot nu }, ]
здесь с = 3 ∙ 108 м/с – скорость электромагнитных волн в вакууме. Тогда
[ delta =mcdot lambda =frac{mcdot c}{ncdot nu }. ]
Ответ: 7.
Записан
В9. Вариант 1.
Протон (q/m = 1,0∙108 Кл/кг) влетает в однородное электростатическое поле со скоростью υ0 в направлении, противоположном силовым линиям поля. Модуль напряжённости электростатического поля E = 20 В/м. Если протон остановится через промежуток времени Δt = 30 мкс, то модуль его скорости υ0 равен … км/с.
Решение: со стороны электростатического поля на протон действует сила F =q∙E , которая сообщает ему ускорение a (ускорение направлено против скорости). Запишем второй закон Ньютона, и кинематический закон зависимости скорости от времени.
[ begin{array}{l} {qcdot E=mcdot a,} \ {upsilon =upsilon _{0} -acdot t.} end{array} ]
Если в уравнение скорости подставить Δt то конечная скорость υ = 0, тогда
[ begin{array}{l} {upsilon _{0} =acdot Delta t,} \ {upsilon _{0} =frac{q}{m} cdot Ecdot Delta t.} end{array} ]
Ответ: 60 км/с.
Записан
В10. Вариант 1.
На участке цепи, состоящем из четырёх резисторов (см. рис.), сопротивлениями R1 = 10,0 Ом, R2 = 20,0 Ом, R3 = 30,0 Ом и R4 = 40,0 Ом подключённых к источнику постоянного тока выделяется максимальная мощность. Если ЭДС источника Е = 20,0 В, то мощность P4, выделяемая в резисторе R4, равна … мВт.
Решение: максимальная мощность в цепи выделяется только в одном случае – при равенстве внешнего и внутреннего сопротивлений: R = r.
Определим общее сопротивление внешней цепи R, зная, каким образом соединены резисторы
[ R=left(frac{1}{R_{1} } +frac{1}{R_{4} } right)^{-1} +left(frac{1}{R_{2} } +frac{1}{R_{3}} right)^{-1}. ]
После подстановки численных данных, R = r = 20 Ом
Воспользуемся законом Ома для замкнутой цепи, и найдём ток
[ I=frac{E}{R+r} =frac{E}{2R}. ]
Напряжение на первом и четвёртом резисторах одинаковое (соединены параллельно), найдём его, воспользовавшись законом ома для участка:
[ U_{14} =Icdot R_{14} =frac{E}{2R} cdot left(frac{1}{R_{1}} +frac{1}{R_{4}} right)^{-1} =frac{E}{2R} cdot frac{R_{1} cdot R_{4} }{R_{1} +R_{4}}. ]
Тогда мощность выделяемая в резисторе R4, равна
[ P_{4} =frac{U_{14}^{2} }{R_{4} } =frac{E^{2} }{4R^{2}} cdot frac{R_{1}^{2} cdot R_{4}}{left(R_{1} +R_{4} right)^{2}}. ]
Ответ: 400 мВт.
Записан
Страницы: 1 … 3 4 [5] 6 7
Источник
30. Молекулярная физика (расчетная задача)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
В калориметре находился (m_1=1) кг льда. Чему равна начальная температура льда, если при добавлении в калориметр (m=50) г воды, имеющей температуру (t_0=20^circ C) , в калориметре установилось тепловое равновесие при (t=-2^circ C)? Теплообменом с окружающей средой и теплоемкостью калориметра пренебречь.
Рассмотрим все процессы, происходящие со льдом и водой.
1) Остывание воды до температуры кристаллизации(0(^circ C)). Количество теплоты, выделившееся при этом: [Q_1=c_1m(t_0-0),] где (c_1) – удельная теплоемкость воды. Так как температура равновесия меньше 0(^circ), то вся вода перейдет в лед.
2) Кристаллизация воды. Количество теплоты: [Q_2=lambda m,] где (lambda) – удельная теплота плавления льда.
3) Охлаждение получившегося льда до -5(^circ). Количество теплоты, которое выделится: [Q_3=c_2 m (0-t)] (c_2) – удельная теплоемкость льда.
4) Нагревание первоначального льда до (t). Количество телоты, необоходимое для нагрева [Q=c_2m_1(t-t_1)] (t_1) – начальная температура льда. Так как теплообменом с окружающей средой и теплоемкостью калориметра пренебречь, то все количество теплоты, которое выделяется при охлаждении воды идет на нагрев льда, а значит: [Q=Q_1+Q_2+Q_3 Rightarrow c_2m_1(t-t_1)=c_1m(t_0-0)+lambda m+c_2 m (0-t)] Выразим начальную температуру льда [t_1=-dfrac{c_1m(t_0-0)+lambda m+c_2 m (0-t)-c_2m_1t}{c_2m_1}] [t_1=-dfrac{4200cdot0,05cdot(20)+330cdot 10^3cdot0,05 + 2100cdot0,05cdot(0-(-2)}{2100cdot1} approx-10^circ C]
Ответ: -10
В калориметре находился лед при температуре (t_1=-5^circ)С. Чему равна начальная масса льда, если при добавлении в калориметр (m=50) г воды, имеющей температуру (t_0=20^circ C) , в калориметре установилось тепловое равновесие при (t=-2^circ C)? Теплообменом с окружающей средой и теплоемкостью калориметра пренебречь.
Растопится ли лед массой 0,5 кг, имеющий температуру 0(^circ)C, за 5 минут, при использовнии нагревательного элемента мощностью (P=500) Вт, если потери энергии в окружающую среду 20%?
Переведем минуты в секунды 5 минут=300 с.
Так как потери энергии в окружающую среду 20%, то КПД нагревателя равен 100%-20% =80%. Количество теплоты, необходимое, чтобы растопить лед находится по формуле: [Q_1=lambda m,quad (1)] где (lambda) – удельная теплота плавления льда, (m) – масса льда. В свою очередь количество теплоты, которое получит лед при нагреве равно: [Q_2=eta P t, quad (2)] где (eta) – КПД нагревателя, (t) – время нагрева. Найдем (Q_1) и (Q_2) [Q_1=330000text{ Дж/кг}cdot 0,5text{ кг}=175500text{ Дж}] [Q_2=0,8cdot 500text{ Вт}cdot300text{ с}=120000text{ Дж}] Так как (Q_1>Q_2), то лед полностью не растает.
Ответ: нет
Большой кусок льда начали нагревать, какая масса льда растает за 11 минут, при использовнии нагревательного элемента мощностью (P=1000) Вт, если потери энергии в окружающую среду 25%, а температура льда 0(^circ)?
Переведем минуты в секунды 11 минут =660 с.
Так как потери энергии в окружающую среду 25%, то КПД нагревателя равен 100%-25% =75%. Количество теплоты, необходимое, чтобы растопить лед находится по формуле: [Q=lambda m,quad (1)] где (lambda) – удельная теплота плавления льда, (m) – масса льда, в свою очередь количество теплоты, которое получит лед при нагреве равно: [Q=eta P t, quad (2)] где (eta) – КПД нагревателя, (t) – время нагрева. Приравняем (1) и (2) [lambda m = eta P t,] выразим отсюда массу льда и найдем ее [m=dfrac{eta P t}{lambda }=dfrac{0,75 cdot1000text{ Вт}cdot660text{ с} }{330000text{ Дж/кг}}=1,5text{ кг}]
Ответ: 1,5
Какую массу дров нужно сжечь на костре, чтобы нагреть до кипения воду массой 2 кг, если 90% теплоты рассеивается в воздух, а начальная температура воды (t_0=20^circ)C. Удельная теплота сгорания дров (q=8,3cdot 10^6)Дж/кг.
Температура кипения воды 100(^circ)С, для того, чтобы нагреть воду необходимо количество теплоты: [Q=cmDelta t,quad (1)] где (c) – удельная теплоемкость воды, (m) – масса воды, (Delta t) – изменение температуры. Так как 90% тепла отдается окружающей среде, то только 10% идет на нагрев воды, а значит количество теплоты, которое идет на нагрев воды от сгорания дров равно: [Q=0,1 q m_1, quad (2)] (m_1) – масса дров. Приравняем (1) к (2) и выразим массу дров. [cmDelta t=0,1 q m_1 Rightarrow m_1=dfrac{cmDelta t}{0,1 q}= dfrac{4200text{Дж/кг$cdot ^circ$С}cdot 2 text{ кг}cdot 80^circ C}{0,1cdot 8,3cdot 10^6text{ Дж/кг}}approx 0,8text{ кг}]
Ответ: 0,8
В теплоизолированном сосуде содержится вода с температурой (t_1=60^circ), в нее кладут металический шарик, нагретый до температуры (t_2=15^circ). В результате установления теплового равновесия, температура воды стала (t_3=40^circ). Найдите температуру воды (t_4), если положить еще 1 такой же шарик (первый остался в сосуде). Ответ дайте в градусах Цельсия округлив до целых.
Запишем уравнение теплового баланса, при добавлении в сосуд первого шарика. [c_text{в}m_text{в}left(t_1-t_3right)=c_text{ м}m_text{ м}left(t_2-t_3right)] где (c_text{в}) – удельная теплоемкость воды, (m_text{в}) – масса воды в сосуде, (c_text{ м}) – удельная теплоемкость металла, (m_text{ м}) -масса шарика.
Отсюда [c_text{ м}m_text{ м}=dfrac{c_text{в}m_text{в}left(t_1-t_3right)}{left(t_2-t_3right)} quad (1)] Запишем уравнение теплового баланса, при добавлении второго шарика [c_text{в}m_text{в}left(t_3-t_4right)+c_text{ м}m_text{ м}left(t_3-t_4right)=c_text{ м}m_text{ м}left(t_2-t_4right) quad (2)] Подставим (1) в (2) и выразим конечную температуру [t_4=dfrac{t_1t_2-2t_2t_3+t_1t_3}{2t_1-t_2-t_3}=dfrac{60^circcdot15^circ – 2cdot 15^circ cdot 40^circ+ 60^circcdot 40^circ}{2cdot 60^circ – 15^circ-50^circ}approx 39^circ]
Ответ: 39
Максим Олегович
????Решаем вариант профиля на 100 баллов
???? А еще сюрприз: мы подводим итоги розыгрыша “Щелчка”!
Математика: ????Решаем вариант профиля на 100 баллов
Источник
Задачи на количество теплоты с решениями
Формулы, используемые на уроках «Задачи на количество теплоты,
удельную теплоемкость».
1 г = 0,001 кг; 1 т = 1000 кг; 1 кДж = 1000 Дж; 1 МДж = 1000000 Дж
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?
При решении задачи нужно учесть, что оба тела – и котёл, и вода – будут нагреваться вместе. Между ними происходит теплообмен. Их температуры можно считать одинаковыми, т. е. температура котла и воды изменяется на 100 °С – 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми. Ведь их массы и удельные теплоёмкости различны.

Задача № 2. Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.

Задача № 3. Стальная деталь массой 3 кг нагрелась от 25 до 45 °С. Какое количество теплоты было израсходовано?

Задача № 4. В сосуде содержится 3 л воды при температуре 20 °С. Сколько воды при температуре 45 °С надо добавить в сосуд, чтобы в нём установилась температура 30 °С? Необходимый свободный объём в сосуде имеется. Теплообменом с окружающей средой пренебречь

Задача № 5. На сколько градусов изменилась температура чугунной детали массой 12 кг, если при остывании она отдала 648000 Дж теплоты?

Задача № 6. По графику определите удельную теплоёмкость образца, если его масса 50 г.
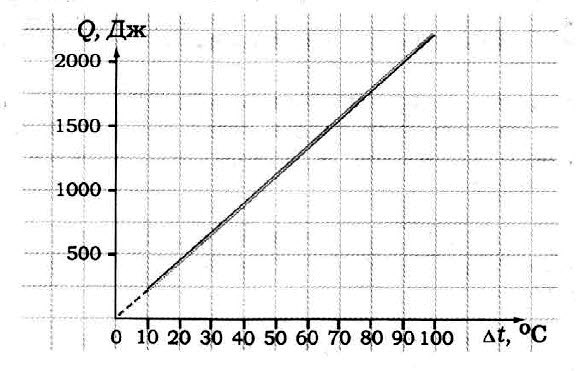

Задача № 7. Для нагревания медного бруска массой 3 кг от 20 до 30 °С потребовалось 12000 Дж теплоты. Какова удельная теплоемкость меди?

Задача № 8. Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей 2,1 кДж энергии. Чему равна удельная теплоемкость камня?
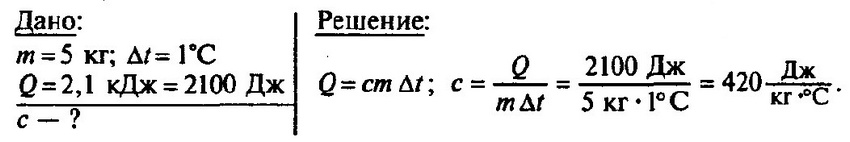
Задача № 9. Какое количество теплоты потребуется для нагревания на 1 °С воды объемом 0,5 л; олова массой 500 г; серебра объемом 2 см3; стали объемом 0,5 м3; латуни массой 0,2 т?

Задача № 10. Какое количество теплоты получили алюминиевая кастрюля массой 200 г и находящаяся в ней вода объемом 1,5 л при нагревании от 20 °С до кипения при температуре 100 °С?

Задача № 11. а) Воздух, заполняющий объем 0,5 л в цилиндре с легким поршнем, нагрели от 0 до 30 °С при постоянном атмосферном давлении. Какое количество теплоты получил воздух?
б) В порожнем закрытом металлическом баке вместимостью 60 м3 под действием солнечного излучения воздух нагрелся от 0 до 20 °С. Как и на сколько изменилась внутренняя энергия воздуха в баке? (Удельная теплоемкость воздуха при постоянном объеме равна 720 Дж/кг-°С.)

Задача № 12. ОГЭ Металлический цилиндр массой m = 60 г нагрели в кипятке до температуры t = 100 °С и опустили в воду, масса которой mв = 300 г, а температура tв = 24 °С. Температура воды и цилиндра стала равной Θ = 27 °С. Найти удельную теплоёмкость металла, из которого изготовлен цилиндр. Удельная теплоёмкость воды св = 4200 Дж/(кг К).

Задача № 13. В теплоизолированном сосуде сначала смешивают три порции воды 100 г, 200 г и 300 г с начальными температурами 20 °C, 70 °C и 50 °C соответственно. После установления теплового равновесия в сосуд добавляют новую порцию воды массой 400 г при температуре 20 °C. Определите конечную температуру в сосуде. Ответ дайте в °C, округлив до целого числа. Теплоёмкостью калориметра пренебрегите.
Решение.

Ответ: 39 °С.
Задача № 14. (повышенной сложности) Стальной шарик радиусом 5 см, нагретый до температуры 500 ˚С, положили на лед, температура которого 0 ˚С. На какую глубину погрузится шарик в лед? (Считать, что шарик погрузился в лед полностью. Теплопроводностью шарика и нагреванием воды пренебречь.)
Дано: R = 0,05 м; t1 = 500 ˚С; t2 = 0 ˚С;
ρ1 (плотность стали) = 7800 кг/м3.;
ρ2 (плотность льда) = 900 кг/м3.
c (удельная теплоемкость стали) = 460 Дж/кг •˚С,
λ (удельная теплота плавления льда) = 3,3 • 105 Дж/кг,
Найти: h – ?

Краткая теория для решения Задачи на количество теплоты.

Конспект урока «Задачи на количество теплоты».
Посмотреть конспект урока по теме «Количество теплоты. Удельная теплоемкость»
Следующая тема: «ЗАДАЧИ на сгорание топлива с решениями».
Источник
