В теплоизолированный сосуд налили воду массой
Задачи на количество теплоты с решениями
Формулы, используемые на уроках «Задачи на количество теплоты,
удельную теплоемкость».
1 г = 0,001 кг; 1 т = 1000 кг; 1 кДж = 1000 Дж; 1 МДж = 1000000 Дж
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?
При решении задачи нужно учесть, что оба тела — и котёл, и вода — будут нагреваться вместе. Между ними происходит теплообмен. Их температуры можно считать одинаковыми, т. е. температура котла и воды изменяется на 100 °С — 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми. Ведь их массы и удельные теплоёмкости различны.

Задача № 2.
Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.

Задача № 3.
Стальная деталь массой 3 кг нагрелась от 25 до 45 °С. Какое количество теплоты было израсходовано?

Задача № 4.
В сосуде содержится 3 л воды при температуре 20 °С. Сколько воды при температуре 45 °С надо добавить в сосуд, чтобы в нём установилась температура 30 °С? Необходимый свободный объём в сосуде имеется. Теплообменом с окружающей средой пренебречь

Задача № 5.
На сколько градусов изменилась температура чугунной детали массой 12 кг, если при остывании она отдала 648000 Дж теплоты?

Задача № 6.
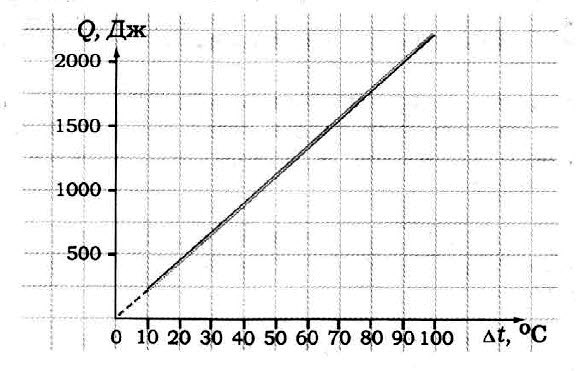
По графику определите удельную теплоёмкость образца, если его масса 50 г.


Задача № 7.
Для нагревания медного бруска массой 3 кг от 20 до 30 °С потребовалось 12000 Дж теплоты. Какова удельная теплоемкость меди?

Задача № 8.
Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей 2,1 кДж энергии. Чему равна удельная теплоемкость камня?
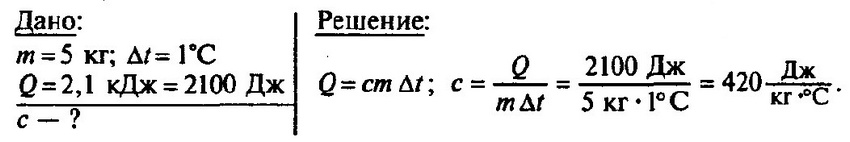
Задача № 9.
Какое количество теплоты потребуется для нагревания на 1 °С воды объемом 0,5 л; олова массой 500 г; серебра объемом 2 см3; стали объемом 0,5 м3; латуни массой 0,2 т?

Задача № 10.
Какое количество теплоты получили алюминиевая кастрюля массой 200 г и находящаяся в ней вода объемом 1,5 л при нагревании от 20 °С до кипения при температуре 100 °С?

Задача № 11.
а) Воздух, заполняющий объем 0,5 л в цилиндре с легким поршнем, нагрели от 0 до 30 °С при постоянном атмосферном давлении. Какое количество теплоты получил воздух?
б) В порожнем закрытом металлическом баке вместимостью 60 м3 под действием солнечного излучения воздух нагрелся от 0 до 20 °С. Как и на сколько изменилась внутренняя энергия воздуха в баке? (Удельная теплоемкость воздуха при постоянном объеме равна 720 Дж/кг-°С.)

Задача № 12.
ОГЭ
Металлический цилиндр массой m = 60 г нагрели в кипятке до температуры t = 100 °С и опустили в воду, масса которой mв = 300 г, а температура tв = 24 °С. Температура воды и цилиндра стала равной Θ = 27 °С. Найти удельную теплоёмкость металла, из которого изготовлен цилиндр. Удельная теплоёмкость воды св = 4200 Дж/(кг К).

Задача № 13.
В теплоизолированном сосуде сначала смешивают три порции воды 100 г, 200 г и 300 г с начальными температурами 20 °C, 70 °C и 50 °C соответственно. После установления теплового равновесия в сосуд добавляют новую порцию воды массой 400 г при температуре 20 °C. Определите конечную температуру в сосуде. Ответ дайте в °C, округлив до целого числа. Теплоёмкостью калориметра пренебрегите.
Решение.

Ответ: 39 °С.
Краткая теория для решения Задачи на количество теплоты.

Конспект урока «Задачи на количество теплоты».
Посмотреть конспект урока по теме «Количество теплоты. Удельная теплоемкость»
Следующая тема: «ЗАДАЧИ на сгорание топлива с решениями».
Источник
1. На рисунке представлен график зависимости температуры t от времени τ для куска льда массой 480 г, помещённого при температуре −20 °С в калориметр. В тот же калориметр помещён нагреватель. Найдите, какую мощность развивал нагреватель при плавлении льда, считая эту мощность в течение всего процесса постоянной. Теплоёмкостью калориметра и нагревателя можно пренебречь. (Удельная теплота плавления льда — 330 кДж/кг.)
Решение.
Чтобы расплавить весь имеющийся лёд необходимо затратить энергию:
Здесь m — масса льда, λ — удельная теплота плавления льда.
Мощность нагревателя W — есть расход энергии в единицу времени. Время плавления определяем по графику:
Тогда, используя табличные данные и данные задачи, получаем:
Ответ: 330 Вт.
2. Сколько граммов воды можно нагреть на спиртовке на 30 °С, если сжечь в ней 21 грамм спирта? КПД спиртовки (с учётом потерь теплоты) равен 30 %. (Удельная теплота сгорания спирта 2,9·107Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг·°С)).
Решение.
При нагревании тела на температуру тело получает количество теплоты При сгорании тела выделяется энергия Учитывая, что КПД спиртовки равен 30 %, получаем:
Ответ: 1450 г.
3. Теплоизолированный сосуд содержит смесь льда и воды, находящуюся при температуре 0 °С. Масса льда 40 г, а масса воды 600 г. В сосуд впускают водяной пар при температуре +100 °С. Найдите массу впущенного пара, если известно, что окончательная температура, установившаяся в сосуде, равна +20 °С.
Решение.
Окончательная температура положительна, значит, весь лед расплавился, и вся получившаяся вода нагрелась.
При этом пар конденсировался и полученная вода остыла. С учетом этого запишем уравнение теплового баланса:
и выразим отсюда массу пара:
Здесь Qпол и Qотд — полученная и отданная теплота соответственно, m1, m2, m3 — массы льда, воды, пара соответственно, λ — удельная теплота плавления льда, c — удельная теплоемкость воды, τ — удельная теплота парообразования, t2 — конечная температура, t1 — исходная температура смеси лед-вода, t3 — температура пара.
Переведя граммы в килограммы и подставляя данные задачи и табличные данные, получаем:
Ответ: 25,4 г.
4. Литровую кастрюлю, полностью заполненную водой, из комнаты вынесли на мороз. Зависимость температуры воды от времени представлена на рисунке. Какое количество теплоты выделилось при кристаллизации и охлаждении льда?
Примечание.
Удельную теплоту плавления льда считать равной
Решение.
Поскольку объём воды равен одному литру, масса воды равна одному килограмму. Таким образом, кристаллизовался 1 кг льда, выделив при этом
Также тепло выделялось при охлаждении льда:
Следовательно, при кристаллизации и охлаждении льда выделилось 372 кДж энергии.
Ответ: 372 кДж.
5. Сколько граммов спирта нужно сжечь в спиртовке, чтобы нагреть на ней воду массой 580 г на 80 °С? КПД спиртовки (с учётом потерь теплоты) равен 20%. (Удельная теплота сгорания спирта 2,9·107Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг·°С)).
Решение.
При нагревании тела на температуру тело получает количество теплоты При сгорании тела выделяется энергия Учитывая, что КПД спиртовки равен 20%, получаем:
Ответ: 33,6 г.
6. Какое количество теплоты выделится при кристаллизации 2 кг расплавленного олова, взятого при температуре кристаллизации, и последующем его охлаждении до 32 °С? (Удельная теплоёмкость олова — 230 Дж/(кг · °С).)
7. Тонкостенный сосуд содержит смесь льда и воды, находящуюся при температуре 0 °С. Масса льда 350 г, а масса воды 550 г. Сосуд начинают нагревать на горелке мощностью 1,5 кВт. Сколько времени понадобится, чтобы довести содержимое сосуда до кипения? Потерями теплоты и удельной теплоёмкостью сосуда, а также испарением воды можно пренебречь.
Решение.
Чтобы довести содержимое сосуда до кипения за время τ, необходимо расплавить лёд, а затем нагреть всю получившуюся воду до температуры кипения, следовательно, затратить энергию, равную
Здесь m1, m2, — массы льда и воды соответственно, λ — удельная теплота плавления льда, c — удельная теплоёмкость воды, t2 — температура кипения воды, t1 — исходная температура смеси лед-вода.
Мощность горелки W есть расход энергии в единицу времени, откуда находим τ:
Подставляя табличные данные и данные задачи, находим:
Ответ: 5,5 мин.
8. На рисунке представлен график зависимости температуры от полученного количества теплоты для вещества массой 1 кг. Первоначально вещество находилось в твёрдом состоянии. Определите удельную теплоёмкость вещества в твёрдом состоянии.
Решение.
Удельная теплоёмкость — это количество теплоты, необходимое для того, чтобы нагреть вещество на 1 °C. Из графика видно, что для нагревания 1 кг вещества на 200 °C потребовалось 50 кДж. Таким образом, удельная теплоёмкость равна:
Ответ:
9. В тонкостенный сосуд налили воду, поставили его на электрическую плитку мощностью 800 Вт и начали нагревать. На рисунке представлен график зависимости температуры воды t от времени τ. Найдите массу налитой в сосуд воды. Потерями теплоты и теплоёмкостью сосуда пренебречь.
10. Какое количество теплоты потребуется, чтобы в алюминиевом чайнике массой 700 г вскипятить 2 кг воды? Первоначально чайник с водой имели температуру 20 °С.
Примечание.
Удельную теплоёмкость алюминия считать равной
Решение.
Для нагревания чайника необходимо
Для нагревания воды:
Всего потребуется
Ответ: 723,52 кДж.
11. Какое количество теплоты выделится при конденсации 2 кг пара, взятого при температуре кипения, и последующего охлаждения воды до 40 °С при нормальном атмосферном давлении?
Решение.
В данном случае тепло отдавали пар и получившаяся из него вода. Пар отдал:
вода отдала:
Таким образом:
Ответ: 5104 кДж.
12. Какое минимальное количество теплоты необходимо для превращения в воду 500 г льда, взятого при температуре −10 °С? Потерями энергии на нагревание окружающего воздуха пренебречь.
Решение.
Для нагревания льда до температуры плавления необходимо:
Для превращения льда в воду:
Таким образом:
Ответ: 175 500 Дж.
13. В сосуд с водой положили кусок льда. Каково отношение массы льда к массе воды, если весь лёд растаял и в сосуде установилась температура 0 °С? Теплообменом с окружающим воздухом пренебречь. Начальные температуры воды и льда определите из графика зависимости температуры t от времени τ для воды и льда в процессе теплообмена.
Решение.
Лёд растает за счёт того, что вода будет остывать и тем самым отдавать своё тепло. Запишем это в формульном виде: где — теплоёмкость воды, — удельная теплота плавления льда, — масса воды и льда соответственно.
Таким образом,
Ответ: 0,42.
14. Как изменится внутренняя энергия 500 г воды, взятой при 20°С, при её превращении в лёд при температуре 0 °С?
Решение.
При охлаждении воды до 0 °С выделится количество теплоты, равное:
Затем при кристаллизации воды выделится количество теплоты, равное:
Таким образом, всего вода отдаст теплоты.
Ответ: 207 кДж.
15. В стакан массой 100 г, долго стоявший на улице, налили 200 г воды из лужи при температуре +10 °С и опустили в неё кипятильник. Через 5 минут работы кипятильника вода в стакане закипела. Пренебрегая потерями теплоты в окружающую среду, найдите мощность кипятильника. Удельная теплоёмкость материала стакана равна 600 Дж/(кг · °С).
16. Два однородных кубика привели в тепловой контакт друг с другом (см. рисунок). Первый кубик изготовлен из цинка, длина его ребра 2 см, а начальная температура t1 = 1 °C. Второй кубик изготовлен из меди, длина его ребра 3 см, а начальная температура t2 = 74,2 °C. Пренебрегая теплообменом кубиков с окружающей средой, найдите температуру кубиков после установления теплового равновесия.
Примечание.
Плотности цинка и меди соответственно:
Удельные теплоёмкости цинка и меди соответственно:
Решение.
При нагревании(охлаждении) тела на температуру тело получает(отдаёт) количество теплоты Более горячее тело передаёт тепло более холодному, запишем уравнение теплового баланса: Заметим, что теплоёмкости цинка и меди равны, поэтому их можно сократить. Раскроем скобки:
Найдём массы кубиков:
Подставим эти значения в формулу для конечной температуры:
Ответ:
17. Сколько литров воды при 83 °С нужно добавить к 4 л воды при 20 °С, чтобы получить воду температурой 65 °С? Теплообменом с окружающей средой пренебречь.
Решение.
Плотность воды равна 1 кг/л, теплоемкость равна 4 200 Дж/кг. Таким образом, изначально мы имеем m0 = 4 кг воды при температуре t0 = 20 °C. Добавляется некоторое количество воды массой m1 при температуре t1 = 83 °C. Конечная температура смеси равна tкон, а её масса m0 + m1.
Составим уравнение теплового баланса для процесса:
— отданное в процессе тепло;
— полученное в процессе тепло;
.
Таким образом,
следовательно, необходимо 10 л воды.
Ответ: 10.
18. В тонкостенный сосуд налили воду массой 1 кг, поставили его на электрическую плитку и начали нагревать. На рисунке представлен график зависимости температуры воды t от времени τ. Найдите мощность плитки. Потерями теплоты и теплоёмкостью сосуда пренебречь.
Решение.
Мощность, это отношение теплоты ко времени, за которую эта теплота получена Теплота, полученная телом при нагревании на температуру рассчитывается по формуле Используя график, найдём мощность плитки:
Ответ: 700 Вт.
19. 3 л воды, взятой при температуре 20 °С, смешали с водой при температуре 100 °С. Температура смеси оказалась равной 40 °С. Чему равна масса горячей воды? Теплообменом с окружающей средой пренебречь.
Решение.
Более холодная вода нагрелась за счет остывания горячей воды: . Масса воды вычисляется по формуле:
Выражаем массу горячей воды:
Ответ: 1.
20. Килограммовый кусок льда внесли с мороза в тёплое помещение. Зависимость температуры льда от времени представлена на рисунке. Какое количество теплоты было получено в интервале времени от 50 мин до 60 мин?
Решение.
Исходя из графика, в интервале от 50 до 60 минут происходил нагрев воды от 0 °C до 20 °C. Вычислим количество теплоты:
Ответ: 84 кДж.
21. В стакан массой 100 г, долго стоявший на столе в комнате, налили 200 г воды при комнатной температуре +20 °С и опустили в неё кипятильник мощностью 300 Вт. Через 4 минуты работы кипятильника вода в стакане закипела. Пренебрегая потерями теплоты в окружающую среду, найдите удельную теплоёмкость материала стакана.
22. Два однородных кубика привели в тепловой контакт друг с другом. Первый кубик изготовлен из меди, длина его ребра 3 см, а начальная температура t1 = 2 °C. Второй кубик изготовлен из алюминия, длина его ребра 4 см, а начальная температура t2 = 74 °C. Пренебрегая теплообменом кубиков с окружающей средой, найдите температуру кубиков после установления теплового равновесия.
Примечание.
Плотности алюминия и меди соответственно:
Удельные теплоёмкости алюминия и меди соответственно:
Решение.
При нагревании(охлаждении) тела на температуру тело получает(отдаёт) количество теплоты Более горячее тело передаёт тепло более холодному, запишем уравнение теплового баланса: Раскроем скобки:
Найдём массы кубиков:
Подставим эти значения в формулу для конечной температуры:
Ответ:
23. Двигатель трактора совершил полезную работу 23 МДж, израсходовав при этом 2 кг бензина. Найдите КПД двигателя трактора.
Решение.
При сгорании 2 кг бензина выделяется теплоты, где — удельная теплота сгорания бензина. КПД рассчитывается по формуле:
Ответ: 25 %.
24. Автомобиль УАЗ израсходовал 30 кг бензина за 2 ч. езды. Чему равна мощность двигателя автомобиля, если его КПД составляет 30%? (Удельная теплота сгорания бензина 4,6·107Дж/кг).
Решение.
Энергия, полученная двигателем от 30 кг бензина КПД определяется как отношение полезной работы к энергии, потребляемой двигателем Мощность двигателя — это отношение полезной работы совершаемой двигателем ко времени:
Ответ: 57,5 кВт.
25. В сосуд с водой положили кусок льда. Каково отношение массы воды к массе льда, если весь лёд растаял и в сосуде установилась температура 0 °С? Теплообменом с окружающим воздухом пренебречь. Начальную температуру воды и льда определите из графика зависимости от времени для воды и льда в процессе теплообмена.
Решение.
Лед растает за счёт того, что вода будет остывать и тем самым отдавать своё тепло. Запишем это в формульном виде: где — удельная теплоёмкость воды, — удельная теплота плавления льда, — масса воды и льда соответственно.
Таким образом,
Ответ: 2,38.
Источник
Здесь представлено 20 задач по динамике для подготовки к олимпиадам по физике из методического пособия В. Грабцевича. Задачи имеют ответы, но предлагаются без готовых решений.
1. Для нагревания некоторого количества воды от 0 °C до кипения (при нормальном атмосферном давлении) понадобилось 15 минут. После этого 1 час 20 минут потребовалось для обращения всей воды в пар при тех же условиях. Определите удельную теплоту парообразования воды. Считать мощность тепловых потерь постоянной. [ L = 2,24 МДж/кг ]
2. В калориметр, содержащий m1 = 250 г воды при температуре t1 = 15 °C, бросили m2 = 20 г мокрого снега. Температура в калориметре понизилась на Δt1 = 5 °C. Сколько воды было в снеге? Теплоемкостью калориметра пренебречь. [ m = 7 г ]
3. Кусок свинца неупруго ударяется о препятствие со скоростью 350 м/с. Какая часть свинца расплавилась, если все количество теплоты, выделившееся при ударе, поглощается свинцом? Температура свинца перед ударом t1 = 27 °C, удельная теплоемкость свинца c = 130 Дж/(кг×°С), удельная теплота плавления свинца λ = 25 кДж/кг, температура плавления свинца tпл = 327 °C. [ α = 0,89 ]
4. В чашке находилось 500 г льда при температуре −5 °C. В нее вливают 200 г воды, имеющей температуру 80 °C. Какая температура установится в чашке? Что в ней находится? [ 385 г воды и 315 г льда при температуре 0 °C. ]
5. При нормальном атмосферном давлении в открытый калориметр помещают одинаковое количество воды (при температуре +t °C) и льда (при температуре –t °C). Какая максимальная доля льда может при этом расплавиться? [ α = 0,63 ]
6. После опускания в воду, имеющую температуру 10 °C, тела, нагретого до 100 °C, через некоторое время установилась общая температура 40 °C. Какой станет температура воды, если, не вынимая тела, в воду опустить еще одно такое же тело, нагретое до 100 °C? Теплоемкостью калориметра и испарением воды пренебречь. [ t = 55 °C ]
7. Свинцовая пуля массой m1 = 9,0 г, имеющая скорость v = 500 м/с и температуру t1 = 250 °C, попадает в стоящую на гладкой горизонтальной поверхности свинцовую гирю массой m1 = 100 г и застревает в ней. Определите конечную температуру пули и гири, если начальная температура гири t2 = 20 °C. Теплообменом с окружающей средой пренебречь. [ t ≈ 112 °C ]
8. На плите стоит кастрюля с водой. При нагревании температура воды увеличилась от 90 °C до 95 °C за одну минуту. Какая доля теплоты, получаемой водой при нагревании, рассеивается в окружающем пространстве, если время остывания той же воды от 95 °C до 90 °C равно 9,0 минутам? [ α = 0,1 ]
9. Электрокипятильник со спиралью сопротивлением 160 Ом поместили в сосуд, содержащий 0,50 л воды при 20 °C и включили в сеть напряжением 220 В. Через 20 минут кипятильник выключили. Сколько воды выкипело? Считать, что вся подводимая теплота пошла на нагревание воды. [ m = 85 г ]
10. Электрический нагреватель имеет три одинаковые спирали. Две параллельно соединенные спирали подключены последовательно с третьей. Нагреватель опущен в сосуд с водой. Спустя τо = 9 мин, когда вода нагрелась от температуры t1 = 20 °С до температуры t2 = 50 °С, спираль в параллельном соединении перегорела. На сколько больше времени из-за этого придется ждать, пока вода закипит? Потери теплоты не учитывать, напряжение на клеммах постоянно. [ Δτ = 5 мин ]
11. Из ведра налили в кастрюлю некоторое количество воды, затем поставили кастрюлю на нагреватель и через 30 минут вода в ней закипела. Тогда из того же ведра зачерпнули еще некоторое количество воды и долили в кастрюлю. При этом температура воды в кастрюле понизилась на 12 °С. Через 5 минут после этого вода в кастрюле закипела. Какова температура воды в вере. Теплообмен воды с внешней средой не учитывать. [ t = 16 °C ]
12. В теплоизолированном сосуде находится смесь льда массой m = 2,1 кг и воды. После начала нагревания температура смеси оставалась постоянной в течение времени t1 = 11 мин, а затем за время t2 = 4 мин повысилась на Δt = 20 °C. Определите массу смеси, если считать, что количество теплоты, получаемое системой в единицу времени, постоянно. Удельная теплота плавления льда λ = 330 кДж/кг, а удельная теплоемкость воды c = 4,2 кДж/(кг×К). Теплоемкостью сосуда пренебречь. [ M = 3 кг ]
13. В комнате на столе стоят два одинаковых стакана. Температура в комнате 20 °C. В первый стакан быстро наливают воду температурой t = 0 °C, а во второй кладут кусочек льда массой Δm = 10 г и той же температуры и наливают m − Δm = 190 г воды температурой 0 °C. Температура воды в первом стакане через время t1 = 2 мин увеличилась на Δt = 1 °C. Через какое время после заполнения второй стакан нагреется до той же температуры? Удельная теплота плавления льда λ = 336 Дж/г, теплоемкость воды c = 4,2 Дж/(г×К). Теплоемкостью стаканов пренебречь. [ τ2 = 10 мин ]
14. Определите температуру воды в сосуде, если в него налили одну кружку воды при температуре t1 = 40 °С, четыре кружки воды при температуре t2 = 30 °С и пять кружек воды при температуре t3 = 20 °С. Потери теплоты не учитывать. [ t = 26 °C ]
15. Железный шарик (ρ = 7800 кг/м3) радиусом R = 10 см, нагретый до температуры t1 = 500 °С, положили на лед, температура которого t2 = 0 °С. На какую глубину погрузится шарик в лед? Теплопроводностью шарика и нагреванием воды пренебречь. Считать, что шарик погрузился в лед полностью. Удельная теплоемкость железа 460 Дж/(кг × °С), удельная теплота плавления льда 3,3×105 Дж/кг, плотность льда 900 кг/м3.
| [ h = ( | 4 | ρ1Rct1 − | 2 | Rρ2λ) | 1 | . ] |
| 3 | 3 | ρ2λ |
16. Известно, что толщина ледников (как и высота гор) ограничена. Оцените максимальную толщину ледника на Земле. Удельная теплота плавления льда λ = 332 кДж/кг. Ускорение свободного падения g = 9,8 м/с2. [ H ≈ 34 км ]
17. Кусок льда с вмерзшими в него свинцовыми дробинками общей массой 200 г осторожно опускают в стакан калориметра, доверху наполненный водой. Часть воды при этом выливается и в дальнейшем теплообмене не участвует. Когда система пришла в состояние теплового равновесия, оказалось, что температура воды в калориметре 20 °С. Начальные температуры воды – 40 °С, льда – (−20 °С). Масса воды в калориметре была 1,2 кг. Определите объемное содержание свинца в куске льда. Теплоемкостью калориметра пренебречь. Удельная теплоемкость воды 4,2×103 Дж/(кг×°C), льда 2,1×103 Дж/(кг×°C), свинца 138 Дж/(кг×°C). Плотность льда 900 кг/м3, свинца 11,3×103 кг/м3. Удельная теплота плавления льда 3,35×105 Дж/кг. [ η ≈ 0,8 % ]
18. Теплоизолированный сосуд частично заполнили водой. Находящийся в комнате точный водяной термометр опускают в воду. На сколько процентов его показание будет отличаться от первоначальной температуры воды, если теплоемкость термометра меньше теплоемкости сосуда с водой в n раз, а температура в комнате по сравнению с температурой сосуда с водой – в m раз?
| [ ε = | m − 1 | 100 % ] |
| m(n + 1) |
19. Из ведра налили в кастрюлю некоторое количество воды, затем поставили кастрюлю на нагреватель и через 30 минут вода в ней закипела. Тогда из того же ведра зачерпнули еще некоторое количество воды и долили в кастрюлю. При этом температура воды в кастрюле понизилась на 12 °С. Через 5 минут после этого вода в кастрюле закипела. Какова температура воды в ведре? Теплообмен воды с внешней средой не учитывать. [ t1 = 16 °С]
20. В теплоизолированный цилиндрический сосуд поместили кусок льда массой M при t = 0 °C и прочно прикрепили ко дну. Затем залили этот лёд водой такой же массой M. Вода полностью покрыла лёд и достигла уровня H = 20 см. Определите, какова была температура воды, если после установления теплового равновесия уровень воды в сосуде опустился на h = 0,4 см. Плотность воды и льда равны 1000 и 920 Дж/(кг×°C) соответственно. Удельная теплота плавления льда λ = 330 кДж/кг.
| [ tB = | λh(ρ − ρЛ) | ≈ 37,7 °C ] |
| cH(ρ + ρЛ) |
Вы читате материалы из пособия для подготовки к олимпиадам по физике. Далее: задачи по электростатике без решений (с ответами).
Источник
