В трех сосудах находятся газы причем для температур и масс
П. МОЛЕКУЛЯРНАЯ ФИЗИКА
Распределение Максвелла и Больцмана
Примеры ответов на задания.
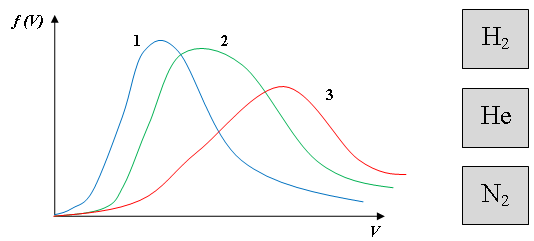
Пример 1.В трех одинаковых сосудах при равных условиях находится одинаковое количество водорода, гелия и азота. Распределение молекул гелия будет описывать кривая…
Ответ: Максимум функции распределения молекул газа по модулю скорости приходится на наиболее вероятную скорость, величина которой определяется формулой: . В нашей задаче имеется три различных газа при одинаковых температурах, поэтому будет тем больше, чем меньше молярная масса газа. Т.к. , то и Распределение молекул гелия будет описывать кривая под номером « 2».
Пример 2. В сосуде, разделенном на две части неподвижной теплоизолирующей перегородкой, находятся одинаковые количества (число молекул) водорода и азота. Если давление газов в обеих частях сосуда одинаково, то распределение скоростей молекул газа в сосуде будет описываться кривыми…
Ответ: Максимум функции распределения молекул газа по модулю скорости приходится на наиболее вероятную скорость, величина которой определяется формулой: . В нашей задаче имеется два различных газа, имеющих одинаковое число молекул и находящихся при одинаковых давлениях. ………
Пример 3.В трех одинаковых сосудах находится одинаковое количество газа, причем Т1> T2 > T3. Распределение проекций скоростей молекул водорода на произвольное направление Х для молекул в сосуде с температурой T3.будет описывать кривая…
Функция распределения молекул газа по проекции скорости на произвольное направление Х имеет вид . При =0 функция принимает вид:
Задания для самостоятельной работы.
Задание 1.На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где – доля молекул, скорости которых заключены в интервале от до в расчете на единицу этого интервала. Для этой функции верным утверждением является…
1)Припонижении температуры площадь под кривой уменьшается.
2) Припонижении температуры максимум кривой смещается вправо.
3) Площадь заштрихованной полоски с ростом температуры будет уменьшаться.
Задание 2.На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где – доля молекул, скорости которых заключены в интервале от до в расчете на единицу этого интервала. Для этой функции верным утверждением является…
1) Суменьшением температуры величина максимума уменьшается.
2) Приизменениитемпературы положение максимума не изменяется.
3) Приизменениитемпературы площадь под кривой не изменяется.
При том же вопросе имеются следующие ответыварианты ответов:
Задание 3. На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где – доля молекул, скорости которых заключены в интервале от до в расчете на единицу этого интервала.
Если не меняя температуры взять другой газ с большей молярной массой и таким же числом молекул, то…
1) величина максимума уменьшится; 2) площадь под кривой увеличится;
3) максимум кривой сместится влево.
Задание 4. На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где – доля молекул, скорости которых заключены в интервале от до в расчете на единицу этого интервала.
Если не меняя температуры взять другой газ с меньшей молярной массой и таким же числом молекул, то…
1) величина максимума увеличится;
2) площадь под кривой уменьшится;
3) максимум кривой сместится вправо, в сторону больших
скоростей.
Задание 5.В трех одинаковых сосудах находится одинаковое количество газа, причем Т1 >Т2> Т3. Распределение скоростей молекул в сосуде с температурой Т1 будет описывать кривая…
Задание 6. На (Р,V) – диаграмме показан процесс, производимый идеальным газом в изолированной сосуде. Начальное и конечное состояния будут соответствовать распределениям скоростей, изображенным на рисунке…
Задание 7.В сосуде, разделенном на две части подвижным теплоизолирующим поршнем, находятся газ, причем количества газа в каждой части сосуда одинаково и для объемов выполняется условие V1 < V2. Распределение скоростей молекул газа в сосуде будет описываться кривыми…
Задание 8.В сосуде, разделенном на равные части неподвижной теплоизолирующей перегородкой, находятся одинаковые количества газа, причем Р1> Р2. Распределение скоростей молекул газа в сосуде будет описываться кривыми…
Задание 9.В сосуде, разделенном на равные части неподвижной непроницаемой перегородкой, находится газ. Температуры газа в каждой части сосуда равны, по массе газа в левой части больше, чем в правой М1> М2. Функция распределения скоростей молекул газа в сосуде будет описываться кривыми…
Задание 10.В трех одинаковых сосудах при равных условиях находится одинаковое количество водорода, гелия и азота. Распределение проекций скоростей молекул азота на произвольное направление Х будет описывать кривая…
Коды верных ответов:
| Номер задания |
| ответ |
©2015-2021 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2016-08-20 Нарушение авторских прав и Нарушение персональных данных
Источник
17.1. В сосуде находится масса m1 = 14 г азота и масса m2 = 9 г водорода при температуре t = 100 С и давлении p = 1 МПа. Найти молярную массу M смеси и объем V сосуда.
17.2. В трех сосудах находятся газы, причем для температур и масс молекул газов имеют место следующие соотношения: Т1 = Т2 = Т3, m01 = m02 = 2m03.
На рисунке схематически представлены графики распределения молекул идеального газа по скоростям (распределение Максвелла) для этих газов, где
– доля молекул, скорости которых заключены в интервале отдов расчете на единицу этого интервала:
Для графиков этих функций верными являются утверждения, что …
Кривая 1 соответствует распределению по скоростям молекул газа в сосуде 2
кривая 3 соответствует распределению по скоростям молекул газа в сосуде 1
кривая 2 соответствует распределению по скоростям молекул газа в сосуде 2
кривая 3 соответствует распределению по скоростям молекул газа в сосуде 3
17.3. Определите, во сколько раз уменьшается концентрация молекул кислорода О2 в атмосфере при изменении высоты от h1 = 0 м до h2 = 10 км от уровня моря и сравните полученный результат с изменением концентрации молекул водорода Н2 в атмосфере при таких же условиях. Температуру считать равной 273 К. Атмосферу считать изотермической.
17.4. На рисунке приведены графики зависимости плотности ρ четырех разных идеальных газов от давления Р при одинаковых температурах. Большей молярной массой обладает газ под номером …
17.5. В запаянном сосуде находится вода, занимая половину сосуда. Найти давление Р и плотность ρ водяного пара при температуре t = 400° С, зная, что при этой температуре вся вода обращается в пар.
17.6. Найти среднюю кинетическую энергию одной молекулы аммиака NH3 при температуре t = 27°С и среднюю энергию вращательного движения этой молекулы при той же температуре.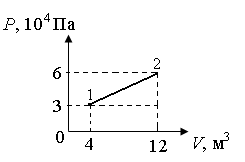
17.7. При переходе из состояния1 в состояние 2 двух атомный газ получает количество теплоты, равное … МДж.
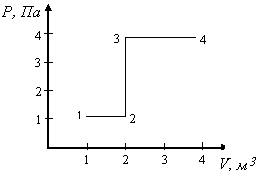
17.8. 14 г азота адиабатически расширяется, причем давление падает от Р1 = 2·105Па до Р2 = 1·105Па. Затем газ нагревается при постоянном объеме до первоначальной температуры Т1 = 420 К. Постройте график процесса в координатах Р – V. Определите приращение внутренней энергии ΔU1-2-3 и работу газа А1-2-3 за весь процесс.
17.9. Во сколько раз увеличится коэффициент полезного действия η цикла Карно при повышении температуры теплоотдатчика от T1 = 380 К до T2 = 560К? Температура теплоприемника T2 = 280 К.
17.10. Изменение энтропии при изобарическом нагревании азота от 0° С до 125° равно ΔS = 39 Дж/К. Чему равна масса азота?
Идз «мкт. Термодинамика» Вариант 18
18.1. За время t = 10 суток из стакана полностью испарилось m = 100 г воды. Сколько в среднем вылетало молекул с поверхности воды за одну секунду?
18.2. В трех одинаковых сосудах при равных условиях находится одинаковое количество водорода, гелия и азота. Распределение молекул гелия будет описывать кривая под номером …
18.3. На какой высоте плотность воздуха при температуре Т = 300 К в е раз (е – основание натурального логарифма) меньше по сравнению с плотностью на уровне моря? Температура воздуха и ускорение свободного падения считайте не зависящими от высоты. Ускорение свободного падения принять равным g= 9,8 м/с2. Молярная масса воздуха М = 0,029 кг/моль.
18.4. На рисунке изображен график зависимости давления Р идеального газа от температуры Т. Какой из приведенных на рисунке участок графика в замкнутом цикле соответствует процессу, происходящему с уменьшением объема?
.
18.5. Средняя кинетическая энергия поступательного движения молекул азота при некоторой температуре равна 2×10-20 Дж, молярная масса азота считать равной M = 28×10-3 кг/моль. Чему равна средняя квадратичная скорость молекул азота при этой температуре?
18.6. Сосуды с газами под давлением 100 и 600 кПа имеют объем 2л и 3л соответственно. Сосуды соединяют небольшой трубкой. Каково установившееся давление в сосудах при неизменной температуре?
18.7. При переходе из состояния 1 в состояние 4 отношение работы , совершенной одно атомным газом в этом процессе, к количеству теплоты, полученного газом, равно
1) 0,29 2) 0,76 3) 0,58 4) 0,93
18.8 Рабочим веществом теплового двигателя является одноатомный идеальный газ. Цикл двигателя состоит из изобарического, адиабатного и изотермического процессов. При изобарическом процессе температура газа увеличивается в два раза. Начальная температура Т1 = 300 К. Постройте график цикла в координатах Р-V. Определите КПД теплового двигателя.
18.9. Газ совершает цикл Карно. Работа изотермического расширения газа A1=5 Дж. Определить работу A2 изотермического сжатия, если термический КПД цикла η = 0,2.
18.10. Смешали воду массой m1 = 5 кг при температуре Т1=280 К с водой массой m2 = 8 кг при температуре Т1=350 К. Найдите температуру смеси Т и изменение энтропии ΔS, происходящее при смешивании.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
1. Зависимость давления от высоты для изотермической атмосферы описывается барометрической формулой . Для этой зависимости справедливы следующие утверждения …
Решение:
Из барометрической формулы следует, что зависимость давления от высоты определяется как температурой газа, так и массой его молекул. Для одного и того же газа с повышением температуры зависимость становится все более слабо выраженной, так что молекулы оказываются распределенными по высоте почти равномерно. При понижении температуры давление на высотах, отличных от нуля, убывает, обращаясь в нуль при . При этом давление определяется весом всего газа и не меняется при изменении температуры. Для разных газов при одинаковой температуре давление газа с более тяжелыми молекулами убывает с высотой быстрее, чем для газа с легкими молекулами.
2. Зависимости давления идеального газа во внешнем однородном поле силы тяжести от высоты для двух разных температур представлены на рисунке.
Для этих функцийверными являются утверждения, что …
Решение:
Зависимость давления идеального газа от высоты для некоторой температуры определяется барометрической формулой: , где давление на высоте , масса молекулы, ускорение свободного падения, постоянная Больцмана. Из формулы следует, что при постоянной температуре давление газа уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура . Давление определяется весом всего газа и не меняется при изменении температуры.
3. Формула описывает распределение одинаковых молекул массой по высоте в изотермической атмосфере; здесь – концентрация молекул при , – их концентрация на высоте . Для этой зависимости справедливы следующие утверждения …
Решение:
Зависимость концентрации молекул идеального газа от высоты для некоторой температуры определяется распределением Больцмана: , где концентрация молекул на высоте , масса молекулы, ускорение свободного падения, постоянная Больцмана. Из формулы следует, что концентрация газа уменьшается с высотой по экспоненциальному закону. При одной и той же температуре молекулы, имеющие меньшую массу, вследствие теплового движения более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне» меньше, чем для более тяжелых молекул (при одинаковом общем количестве молекул). Для молекул, имеющих бόльшую массу, скорость изменения концентрации выше. С другой стороны для одного и того же газа чем выше температура, тем выше интенсивность хаотического теплового движения, и концентрация молекул газа на «нулевом уровне» меньше концентрации тех же молекул при более низкой температуре. При этом скорость уменьшения концентрации при увеличении высоты при боле высокой температуре ниже, то есть экспоненциальный спад более пологий.

4. На рисунке представлены графики функций распределения молекул идеального газа во внешнем однородном поле силы тяжести от высоты для двух разных газов, где массы молекул газа (распределение Больцмана).
Для этих функций верными являются утверждения, что …
Решение:
Зависимость концентрации молекул идеального газа от высоты для некоторой температуры определяется распределением Больцмана: , где концентрация молекул на высоте , масса молекулы, ускорение свободного падения, постоянная Больцмана. Из формулы следует, что при постоянной температуре концентрация газа больше там, где меньше потенциальная энергия его молекул , и уменьшается с высотой по экспоненциальному закону. При одной и той же температуре молекулы, имеющие меньшую массу, более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне» уменьшается, а на высоте увеличивается.
5. В трех одинаковых сосудах при равных условиях находится одинаковое количество водорода, гелия и азота
На рисунке представлены графики функций распределения молекул идеального газа по скоростям (распределение Максвелла), где – доля молекул, скорости которых заключены в интервале скоростей от до в расчете на единицу этого интервала.
Для этих функций верными являются утверждения, что …
Решение:
Функция Максвелла имеет вид .
Полная вероятность равна: , то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости , при которой функция максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. Если сравнивать распределения Максвелла по скоростям различных газов при одной и той же температуре, то при увеличении массы молекулы газа максимум функции сместится влево, следовательно, высота максимума увеличится. Наибольшая масса молекул у азота, меньше у гелия и еще меньше у водорода.
6. В трех сосудах находятся газы, причем для температур и масс молекул газов имеют место следующие соотношения: , На рисунке схематически представлены графики функций распределения молекул идеального газа по скоростям (распределение Максвелла) для этих газов, где – доля молекул, скорости которых заключены в интервале скоростей от до в расчете на единицу этого интервала:
Для графиков этих функций верными являются утверждения, что …
Решение:
имеет смысл площади, ограниченной кривой распределения и осью абсцисс, и численно равен доле молекул, скорости которых имеют всевозможные значения от 0 до . Так как этому условию удовлетворяют все молекул, то и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости , при которой функция максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. При увеличении массы молекул значение наиболее вероятной скорости уменьшается, следовательно, максимум функции сместится влево и высота максимума увеличится.
7. В трех одинаковых сосудах находится одинаковое количество газа, причем
На рисунке представлены графики функций распределения молекул идеального газа по скоростям (распределение Максвелла), где – доля молекул, скорости которых заключены в интервале скоростей от до в расчете на единицу этого интервала.
Для этих функций верными являются утверждения, что …
Решение:
Полная вероятность равна: , то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости , при которой функция максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится.
8. На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где – доля молекул, скорости которых заключены в интервале скоростей от до в расчете на единицу этого интервала.
Если, не меняя температуры взять другой газ с меньшей молярной массой и таким же числом молекул, то …
Решение:
Функция Максвелла имеет вид .
Полная вероятность равна: , то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры или массы молекул не изменяется. Из формулы наиболее вероятной скорости , при которой функция максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. Если сравнивать распределения Максвелла по скоростям различных газов при одной и той же температуре, то при уменьшении массы молекул газа максимум функции сместится вправо, следовательно, высота максимума уменьшится.
9. На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где – доля молекул, скорости которых заключены в интервале скоростей от до в расчете на единицу этого интервала:
Для этой функции верными являются утверждения …
Решение:
Из определения функции распределения Максвелла следует, что выражение определяет долю молекул, скорости которых заключены в интервале скоростей от до (на графике это – площадь заштрихованной полоски). Тогда площадь под кривой равна и не изменяется при изменении температуры и числа молекул газа. Из формулы наиболее вероятной скорости (при которой функция максимальна) следует, что прямо пропорциональна и обратно пропорциональна , где и – температура и молярная масса газа соответственно.
10. На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где – доля молекул, скорости которых заключены в интервале скоростей от до в расчете на единицу этого интервала:
Для этой функции верными являются утверждения …
Решение:
Из определения функции распределения Максвелла следует, что выражение определяет долю молекул, скорости которых заключены в интервале скоростей от до (на графике – площадь заштрихованной полоски). Тогда площадь под кривой равна и не изменяется при изменении температуры. Из формулы наиболее вероятной скорости (при которой функция максимальна) следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится.
Источник
