В верхний сосуд поступает
4.1.Через цилиндрический насадок,
расположенный в стенке, расходуется
вода в количестве
л/с. Диаметр насадка
см, длина
см. Определить напорHнад
центром насадка, скорость
и давление
в насадке (в сжатом сечении).
Р
ешение.Длина насадка
см
,
следовательно, можно принять коэффициент
расхода μ=0,82. Приd=3,8смплощадь
см2. Напор над центром насадка
найдем из формулы
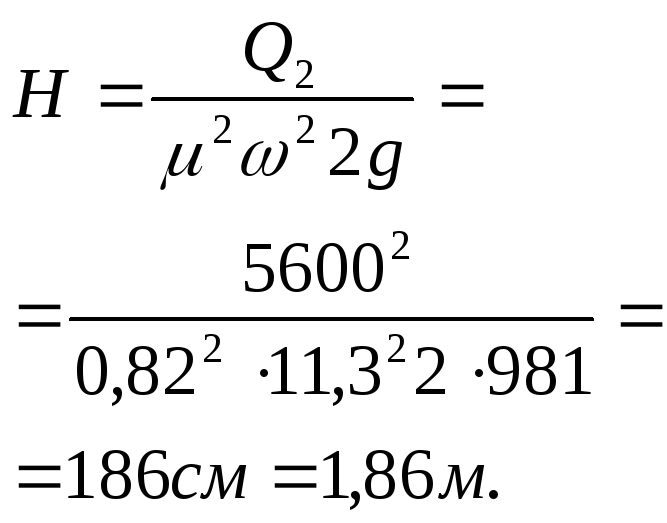
Скорость в выходном сечении насадка
составит
Из условия неразрывности
определим скорость в сжатом сечении,
полагая
,
Для определения давления
составим уравнение Бернулли для двух
сеченийО-ОиС-С при плоскости
сравнения, проходящей через ось насадка
,
Так как между сечениями будут потери
только на сопротивление тонкой стенки,
то
.
Полагая
,
имеем
.
Подставляя численные значения, получим
высоту давления
:
Давление
Недостаток до атмосферного давления в
сжатом сечении
Высота вакуума, выраженная в метрах
водяного столба,
Такой же результат получим, применив
формулу
Ответ:
4.2. Резервуар разделен на три отсека
перегородками, в которых имеются
отверстия: в первой перегородке
прямоугольное с площадью
см2, во второй перегородке –
квадратное, примыкающее одной сторонойа=4смк дну. В наружной стенке
отверстие круглоеd=3,0см. Разность между отметкой уровня
воды в первом отсеке и отметкой центра
наружного отверстияH= 3,10м.
Определить расход воды из резервуара
и напоры
,
и
при установившемся движении в двух
расчетных случаях:
при
истечении воды из наружного отверстия
в атмосферу;в случае
если к наружному отверстию присоединен
цилиндрический насадок.
Решение. 1) Согласно условию сумма
напоров
,
причем любой из этих напоров
,
определяется формулой
.
Подставляя выражение
в исходное уравнение, получим:
.
Прямоугольное и круглое отверстия
полагаем находящимся в условиях полного
совершенного сжатия, поэтому считаем
.
Для квадратного отверстия, расположенного
у дна, коэффициент расхода определим
по формуле
Подставляя числовые значения
,
,H, определим расход
по формуле
По найденному расходу вычислим напоры
;
;
.
Проверка дает
.
2) Если к выходному отверстию присоединим
насадок, то некоторый период времени
движение в отсеках будет неустановившимся.
Через насадок пойдет большой расход
(по сравнению с расходом через отверстие),
но напор
будет падать, так как для пропуска
большего расхода должны увеличиться
напоры
и
.
После того, как движение примет
установившейся характер, будет применимо
уравнение для расхода, из которого
определим, полагая
,
расход
и напоры
;
;
.
При этом, как и в первом случае,
.
Ответ: 1)
2)
4.3. Определить расход из резервуара
через два цилиндрических насадка и
величину вакуума в них. Один насадок
расположен горизонтально в боковой
стенке резервуара на расстоянии
смот дна, другой – вертикально в дне
резервуара. Размеры насадков одинаковы:
см,
см.
Глубина воды в резервуаре
см.
Решение.1) Напор над центром
горизонтального насадка
.
Пренебрегая скоростью подхода, так как
размеры резервуара достаточно велики,
примем
.
Расход из горизонтального насадка
.
Вакуум в сжатом сечении горизонтального
насадка
.
2) Расход через насадок, расположенный
в дне резервуара, соответствует напору
.
Скоростью подхода, как и в первом случае,
пренебрегаем
Расход
из резервуара через оба насадка будет
.
Для определения вакуума в сечении
составим уравнение Бернулли для сечений1–1и
,
взяв плоскость сравнения на уровне
,
.
Отсюда, принимая потери на сопротивление
тонкой стенки, получим выражение высоты
вакуума
или
.
Полагая
и
,
получим:
.
Подставляя числовые значения величин
,
,
,
,
~
0 и принимаяа~
,
будем иметь:
,
или
.
Для условий задачи величина вакуума в
вертикальном насадке будет
.
Ответ: 
;
;
.
4.4. Из резервуара с площадью поперечного
сечения
через отверстие в стенке вода поступает
в смежный резервуар, имеющий площадь
.
Отверстие
расположено на высоте
от дна. Через какое времяtпосле открытия отверстия из первого
резервуара во второй вытечет вода в
количестве
,
если в момент открытия отверстия глубина
в первом резервуаре была
,
а второй был пуст. Притока в резервуары
извне нет.
Р
ешение.Времяtбудет состоять
из двух периодов:
а) истечение при переменном напоре в
атмосферу за время наполнения второго
резервуара до центра отверстия;
б) истечения при переменном напоре под
переменный уровень.
Объем во втором резервуаре от дна до
отметки центра отверстия
.
При вытекании во второй резервуар
количества воды в объеме
уровень воды в первом резервуаре
понизиться на
.
Время
уменьшения напора от
добудет найдено по формуле
.
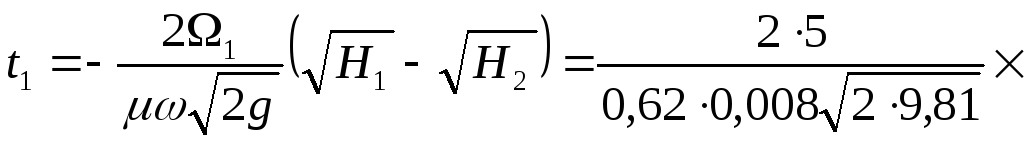
По условию во второй резервуар ещё
должно поступить количество воды
.
При вытекании
воды уровень в первом резервуаре
понизиться на
.
Одновременно уровень воды во втором
резервуаре повыситься на
.
Изменение напора будет от
до
.
Время
на этот процесс определиться по формуле
.
Суммарное искомое время будет
.
Ответ: 
.
4.5. Цилиндрический бак с площадью
и высотой
,
заполненный до краев водой, нужно
опорожнить за время
.
Определить необходимую для этого
площадь двух одинаковых отверстий, одно
из которых расположено в центре дна,
другое в стенке, на половине высоты
бака.
Решение.Опорожнение верхней половины
бака будет определяться дифференциальным
уравнением
,
отсюда
.
Освобождаясь от иррациональностей в
знаменателе и подставляя пределы при
опорожнение верхней половины резервуара,
получим
.
Вводя переменную
,
пределы которой будут от
до
,
перепишем уравнение:
.
В результате интегрирования получим
.
Опорожнение нижней половины бака
определиться по формуле
.
По условию задачи
.
Подставляя числовые значения, получим:
,
отсюда
.
Ответ: 
.
4.6. Цилиндрический резервуар имеет
площадь поперечного сечения
.
В его стенке на расстоянии
от дна расположено круглое отверстие
см.
Постоянный приток воды в резервуар
Определить глубину воды
в резервуаре через 20минпосле
открытия отверстия, если в момент его
открытия глубина равнялась
.
Решение.Расход через отверстие при
напоре
и
будет
.
Так как начальный расход
меньше притока
,
то напор над отверстием увеличивается.
Сначала определим напор
,
при котором приток
и расход из отверстия будут одинаковы.
Из формулы найдем напор
.
Изменение напора от
до
в цилиндрическом резервуаре при наличии
притока
за время
определяется формулой.
или, упрощая уравнение (и полагая
),
получим:
.
Из этого уравнения подбором определим
.
Следовательно, через
после открытия отверстия глубина в
резервуаре будет
.
Ответ: 
.
4
.7.Щитовое отверстие имеет ширину
и высоту
.
Щит приподнимается равномерно со
скоростью
.
Определить объем воды
,
вытекающий за время
полного открытия отверстия. Напор над
центром отверстия
.
Истечение свободное. Коэффициент расхода
отверстия
.
Решение:
Объем воды, вытекающий из отверстия за
время
.
Расход из отверстия
,
где
и
– переменные, определяемые скоростью и
временем открытия,
и
.
Тогда
.
Полный объем за время открытия щита
.
Для решения интеграла введем подстановку
При этом пределы переменной yбудут отHдо
.
.
Решение интеграла дает
.
Подставляя числовые значения в решение,
получим объем
.
Ответ: 
.
4.8. В верхний сосуд поступает вода
с расходомQ = 0,25л/с, которая затем перетекает через
малое от верстие в дне диаметромd1=
10ммв нижний сосуд, имеющий также
малое отверстие в дне диаметромd2= 15мм.
Определить:
а) напоры Н1 иН2в
обоих сосудах;
б) при каком диаметре d2
напорН2будет вдвое меньше,
чемН1.
Решение:
а) Определим в обоих сосудах напоры Н
1 и Н2, при которых
расходыQ1 иQ2 станут равными притоку водыQ= 0,25л/с.Расход
откуда
см =1,35 м;
см
=0,27 м;
б) Находим диаметр d2,
при котором
см
= 0,675 м.
Из формулы
определяем
см2
Тогда
Ответ:d=0,012 м.
4.9.Открытый понтон, имеющий форму
прямоугольного параллелепипеда с
ширинойВ= 2м; длинойL= 5м;
высотойН= 0,5ми весомG= 1000 кг получил в дне пробоину диаметромd. Считая пробоину
затопленным отверстием в тонкой стенке,
определить время, в течение которого
понтон затонет, еслиd= 15мм:
Решение.1) Определим осадку понтона
до получения пробоины:
2) Найдем расход воды через пробоину при
напоре h:
3) Найдем увеличение глубины воды
в понтоне в результате притока за
секунду
4) Определим осадку понтона от поступающей
в него воды за секунду
Как видим,
.
Значит, напор над пробоинойостается
постоянным в течение всего времени
погружения понтона.
5) Понтон затонет, когда его вес станет
равным
или когда в него поступит объем воды
,
откуда время от момента получения
пробоины до затопления понтона
с= 7ч30 мин.
Ответ:7ч30 мин.
4.10.Из закрытого сосуда диаметромD= 0,5м, в верхнюю крышку которого
вставлена открытая трубка, вода вытекает
в атмосферу через малое отверстие в дне
диаметромd= 15мм.
Определить время опорожнения сосуда
при Н= 1,2миh= 0,5м.
Решение.1) При опорожнении сосуда в
силу закона Бойля — Мариотта давление
на его поверхности уменьшается, вследствие
чего в открытой трубке уровень воды
быстро понизится до положения1–1.
С этого момента воздух через трубку
будет прорываться в верхнюю часть
сосуда. Так как во всех точках горизонтальной
плоскости1–1давление одинаково,
то давление
будет оставаться постоянным и равным
атмосферному давлению.
2) Исходя из этого, найдем сначала время,
за которое вытечет объем воды, находящийся
выше уровня 1–1
м3;
= 0,000344м3/с;
с.
3) Время, за которое вытечет оставшийся
объем воды
м3,
найдем по формуле
4) Полное время опорожнения сосуда
с = 16 мин10 с.
Ответ:t =16 мин10 с.
4.11.Цилиндрическая бочка радиусомR= 0,3ми высотойh= 1мзалита водой , давление на свободной
поверхности которой равно атмосферному.
Определить время опорожнения бочки
через отверстие диаметромd= 2смв боковой стенке при горизонтальном
положении.
Решение.1) Составим дифференциальное
уравнение опорожнения непризматического
сосуда, для чего рассмотрим этот процесс
в течение бесконечно малого отрезка
времениdt, за который площадь зеркала
воды в бочкеи напор
z над отверстием меняются весьма
незначительно. Пусть за времяdtуровень воды в бочке опустился на
величинуdz. Тогда объем вытекшей
воды за отрезок времениdt
где dz— отрицательная величина,
так как изменение напораzпроисходит
против положительного направления оси
OZ. Кроме того, элементарный объем равен
где — площадь
отверстия.
Приравнивая правые части выражений
для dW, получаем дифференциальное
уравнение
интегрируя которое, можем найти время
опорожнения бочки.
2) Найдем площадь зеркала воды в
бочке как функцию
z:
3) Подставляя значение
в дифференциальное уравнение и
интегрируя от 2rдо 0, получаем
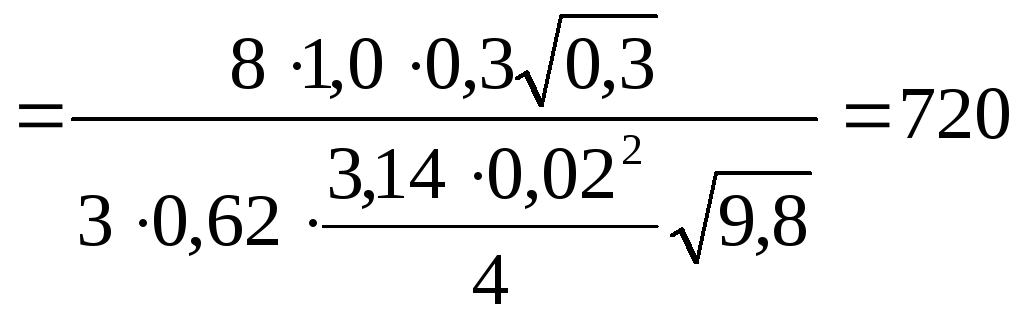с= 12мин.
Ответ:t= 720с.
4.12.Вода расходомQ= 15л/споступает в бак, разделенный
на два отсека перегородкой толщиной 30мм, в которой просверлено четыре
ряда отверстий диаметромd1=
10мм, причем расстояние между центрами
отверстий в ряду и между рядами отверстийа= 50мм. Из второго отсека вода
вытекает через внешний конический
насадок диаметромd2= 80мм.
Определить глубинуH1иH2в обоих отсеках, если в одном ряду 48
отверстий.
Решение.1) ГлубинуН2во
втором отсеке найдем из условия, что
заданный расходQ =15л/спроходит через отверстия в
перегородке и через конический насадок:
откуда
2) Для определения H1воспользуемся
формулой для расхода через затопленное
отверстие, в которойH= =Н1 –H2;
считая, что приа= 50ммвсе
отверстия в перегородке работают как
внешние цилиндрические насадки независимо
друг от друга, имеем
где n= 48
4 = 192 — количество отверстий в перегородке.
Отсюда получаем
Ответ: 
1Размерность основных физических величин
и их производных, применяемых в
гидравлике, приведены в приложении.
2Для приобретения навыка перевода единиц
измерения из СИ во внесистемные единицы,
задачи решены с использованием систем
единиц измерения СГС и МКГСС.
109
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Кафедра гидравлики
ГИдравлика
Контрольная работа по гидравлике
Вариант № 87
Галиуллин Альберт Рафаилович
ФБФО 2СЗ-2, шифр 13-387
Санкт-Петербург
Содержание
Задача 1 ……………………………………………………………………………… 3
Задача 2 ……………………………………………………….……………………. 4
Задача 3 …………………………….………………………………………………. 5
Задача 4 …………………………………………………………………………….. 8
Задача 5 …………………………………………………………………………… 12
Задача 6 …………………………………………………………………………… 13
Задача 7 …………………………………………………………………………… 15
Задача 11 ………………………………………………………………………… 17
Список литературы ……………………………………………………………… 19
Задача 1
В закрытом резервуаре имеется вода, h1 = (50 + 0,1 y) см и масло, h2 = (30 + 0,1 z) см плотностью ρм = 800 кг/м3. Найти давление р0 на поверхности масла в резервуаре, если показание ртутного прибора h = (40 + 0,2 y) см (рис.1).
Рис. 1
Дано:
y = 8; z = 7
Найти:
р0 – ?
Решение:
Для двух точек горизонтальной плоскости 0-0, которые могут быть соединены в пределах однородной жидкости выполняется условие: рА = рВ,
где рА – атмосферное давление на границе раздела ртути и воздуха;
рВ – давление в левом колене манометра.
Воспользуемся основным уравнением гидростатики, согласно которому давление в любой точке покоящейся жидкости можно определить по формуле:
где р0 – давление над свободной поверхностью жидкости;
ρ – плотность жидкости;
g – ускорение свободного падения, равно 9,81 м/с2;
h – заглубление точки под свободную поверхность жидкости.
Тогда, пренебрегая плотность газа, находящегося над свободной поверхностью жидкости, можно записать: .
Откуда .
Учитывая, что согласно плотность ртути, равна , получим
35206,128 Па = 35,2 кПа.
Ответ:давление на поверхности масла в резервуаре, равна р0 = 35,2 кПа.
Задача 2
В вертикальной стенке резервуара с водой на глубине h = (0,8 + 0,1 y) м имеется круглая труба d = (0,2 + 0,05 z) м. Внутренняя кромка трубы срезана под углом α = (45 + 0,2 y)° и закрывается крышкой, вращающейся на верхнем шарнире. Определить усилие T, необходимое для поднятия этой крышки, пренебрегая ее весом и трением в шарнире (рис. 2).
Рис. 2
Дано:
y = 8; z = 7
Найти:
T – ?
Решение:
Минимально необходимую силу для открытия затвора определим из условия его равновесия
т.е. равенства нулю суммы моментов всех сил, действующих на затвор, относительно оси вращения О.
Сила давления на плоскую стенку определяется по формуле: ,
где ρ – плотность жидкости;
g – ускорение свободного падения, равно 9,81 м/с2;
hc – расстояние от центра тяжести площади стенки F до свободной поверхности жидкости. В данном случае ;
S – смоченная площадь стенки. Для эллипса ;
где α – длина малой полуоси эллипса, ;
b – длина большой полуоси эллипса, .
Точка пересечения линии действия силы с плоскостью стенки определяется по формуле ,
где e – эксцентриситет;
где Ic– осевой момент инерции площади затвора относительно центра тяжести;
Тогда можно записать:
Ответ:усилие, необходимое для поднятия крышки, равно .
Задача 3
Определить величину и направление силы гидростатического давления воды на цилиндрический затвор диаметром d = (2 + 0,05 y) м и длиной L = (5 + 0,02 z) м, перегораживающий канал шириной b = (5 + 0,02 z) м, если глубина воды с одной стороны Н = (3 + 0,05 y) м, с другой h = (1 + 0,05 z) м (рис. 3).
Рис. 3
Дано:
y = 8; z = 7
Найти:
P – ?; α – ?
Решение:
В общем случае для криволинейной стенки сила избыточного гидростатического давления определяется по двум составляющим, горизонтальной и вертикальной:
Горизонтальная составляющая определяется по формуле:
где ρ – плотность жидкости;
g – ускорение свободного падения, равно 9,81 м/с2;
hc – расстояние от центра тяжести площади стенки S до свободной поверхности жидкости;
S – площадь проекции стенки на вертикальную плоскость.
Вертикальная составляющая силы давления, воспринимаемой криволинейной стенкой, равна силе тяжести жидкости в объеме VВ, который ограничен стенкой, пьезометрической плоскостью и вертикальной проектирующей поверхностью, построенной на контуре стенки, и определяется по формуле:
где VВ – сила тяжести в объеме.
Запишем
Определим площадь SВ поперечного сечения тела давления. Приближенно рассматриваем ее как сумму трех составляющих:
где
Подставляя числовые значения, получим:
Сила PВ направлена вертикально вверх (см. рис.). Приближенно считаем, что линия ее действия проходит через центр тяжести затвора.
Определим составляющую силы давления на затвор со стороны жидкости, находящейся слева от него.
Определим горизонтальную составляющую силы давления на затвор со стороны жидкости, находящейся справа от него.
Определим линии действия сил. Линия действия горизонтальной составляющей силы PГ смещена вниз на расстояние, равное эксцентриситету.
где Ic– осевой момент инерции проекции стенки на вертикальную плоскость относительно центра тяжести;
Аналогично:
Суммируем полученные силы, приводя к горизонтальной и вертикальной равнодействующей, исходя из условия, что момент равнодействующей равен сумме моментов составляющих.
Равнодействующая горизонтальных составляющих:
Определим линию действия указанной равнодействующей:
Таким образом, результирующая сила P имеет значение
и накоплена к горизонту под углом
Ответ:величина и направление силы гидростатического давления воды на цилиндрический затвор, равны
Задача 4
Определить расход воды в наклонном стальном трубопроводе длиной L = (120 + 5 y) м, построить напорную и пьезометрическую линии, если длина первого участка L1 = (75 + 2 z) м, его диаметр D1 м. Диаметр второго участка D2 мм, напор в баке Н = (4,5 + 0,2 y) м. Отметка начала трубопровода zн = (5 + 0,1 y) м, в конце – zк = (3,5 + 0,1 z) м, температура воды в трубопроводе t = 15°С (рис. 4).
Численные значения диаметров взять из табл. 1.
Указание.В первом приближении при решении задачи следует принимать квадратичную область гидравлических сопротивлений и затем уточнить
значение λ.
Рис. 4
Дано:
y = 8; z = 7
Решение:
Запишем уравнение Бернулли для сечения 1-1 и 2-2. Сечение 1-1 совпадает с со свободной поверхностью жидкости в баке, а сечение 2-2 – с выходным сечением трубопровода. За плоскость сравнения принимаем плоскость 0-0. Тогда
где z1, z2– геометрический напор в соответствующем сечении;
p1, p2 – давление в сечении;
1, 2 – скорость потока жидкости в сечении;
ρ – плотность жидкости;
g – ускорение свободного падения, равно 9,81 м/с2;
h1-2 – потери напора между сечениями 1-1 и 2-2.
Считаем, что площадь поперечного сечения бака достаточно велика, чтобы пренебречь скоростью движения жидкости в нем. Тогда:
В данном случае удобно воспользоваться условием неразрывности потока
где – площадь поперечного сечения потока, в данном случае трубы.
Тогда можно записать:
Следовательно, первое выражение можно записать следующим образом:
Потери между сеч?