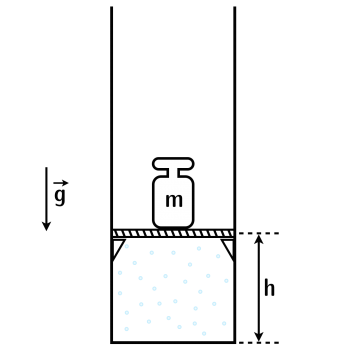
В вертикально расположенном цилиндрическом сосуде на высоте
Источник
2011 год 109 вариант СЗ
В сосуде лежит кусок льда. Температура льда t1 = 0°С. Если сообщить ему количество теплоты Q = 50 кДж, то 3/4 льда растает. Какое количество теплоты q надо после этого сообщить содержимому сосуда дополнительно, чтобы весь лёд растаял и образовавшаяся вода нагрелась до температуры t2 = 20°С? Тепловыми потерями на нагрев сосуда пренебречь.
(Решение)
2011 год. 01-2 вариант. С3
В бутылке объемом V = 1 л находится гелий при нормальном атмосферном давлении. Горлышко бутылки площадью S = 2 см2 заткнуто короткой пробкой, имеющей массу m = 20 г. Если бутылка лежит горизонтально, то для того, чтобы медленно вытащить из ее горлышка пробку, нужно приложить к пробке горизонтально направленную силу F = 1 Н. Бутылку поставили на стол вертикально горлышком вверх. Какое количество теплоты нужно сообщить гелию в бутылке для того, чтобы он выдавил пробку из горлышка? (Решение)
2011 год. 01-1 вариант. С3
Один моль идеального одноатомного газа переводят из состояния 1 с температурой Т1 = 300 К в состояние 2 таким образом, что в течение всего процесса давление газа возрастает прямо пропорционально его объему. В ходе этого процесса газ получает количество теплоты Q = 14958 Дж. Во сколько раз n уменьшается в результате этого процесса плотность газа? (Решение)
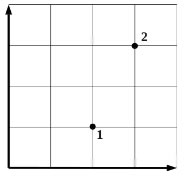 2010 год. 11 вариант. С1
2010 год. 11 вариант. С1
В кабинете физики проводились опыты с разреженным газом постоянной массы. По невнимательности ученик, отметив на графике начальное и конечное состояния газа (см. рисунок), не указал, какие две величины из трёх (давление р, объём V, температура Т) отложены по осям. В журнале осталась запись, согласно которой названные величины изменялись следующим образом: p1 < р2, V1 > V2, Τ1 < Ί2. Пользуясь этими данными, определите, какие величины были отложены на горизонтальной и вертикальной осях. Ответ поясните, указав, какие физические закономерности вы использовали. (Решение)
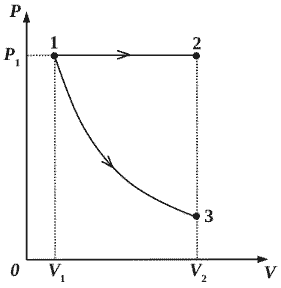 2010 год
2010 год
304 вариант СЗ
Некоторое количество одноатомного идеального газа расширяется из одного и
того же начального состояния (p1, V1) до одного и того же конечного объёма V2
первый раз по изобаре, а второй – по адиабате (см. рисунок). Отношение количества теплоты Q12, полученного газом на изобаре от нагревателя, к модулю изменения внутренней энергии газа |U3 — U1| на адиабате k = Q12/|U3 — U1| = 6 . Чему равно
отношение х работы газа на изобаре А12 к работе газа на адиабате А13? (Решение)
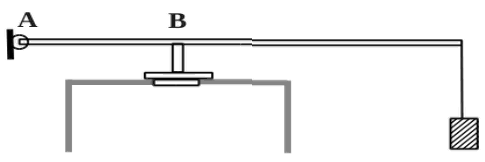 2010 год. 135 вариант. С5
2010 год. 135 вариант. С5
В цилиндр закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие площадью 5·10-4 м2, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии невесомым стержнем длиной 0,5 м, который может свободно поворачиваться вокруг оси в точке А (см. рисунок). Расстояние АВ равно 0,1 м. К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через
580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите объём цилиндра. (Решение)
2009 год. 133 вариант. С1
В цилиндрическом сосуде под поршнем длительное время находятся вода
и ее пар. Поршень начинают вдвигать в сосуд. При этом температура
воды и пара остается неизменной. Как будет меняться при этом масса
жидкости в сосуде? Ответ поясните. (Решение)
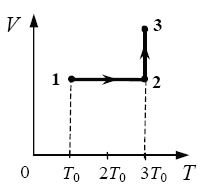 2009 год. 133 вариант. С3
2009 год. 133 вариант. С3
Один моль одноатомного идеального газа
переходит из состояния 1 в состояние 3 в
соответствии с графиком зависимости его объёма
V от температуры T (T0 = 100 К). На участке 2 − 3
к газу подводят 2,5 кДж теплоты. Найдите
отношение работы газа А123 ко всему количеству
подведенной к газу теплоты Q123. (Решение)
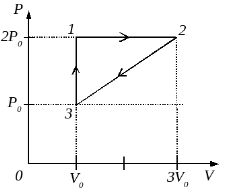 2009 год. 304 вариант. С3
2009 год. 304 вариант. С3
Постоянная масса одноатомного идеального газа совершает циклический процесс, показанный на рисунке. За цикл от нагревателя газ получает количество теплоты QH = 8 кДж. Какую работу совершают внешние силы при переходе газа из состояния 2 в состояние 3?
(Решение)
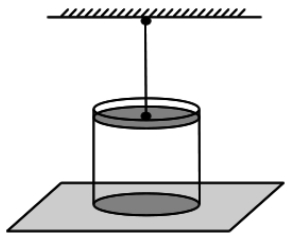 2008 год. 131 вариант. С2
2008 год. 131 вариант. С2
Разогретый сосуд прикрыли поршнем, который с помощью вертикальной нерастяжимой нити соединили с потолком. На сколько процентов от начальной понизится температура воздуха в сосуде к моменту, когда сосуд оторвется от поверхности, на которой он расположен? Масса сосуда 5 кг. Поршень может скользить по стенкам сосуда без трения. Площадь дна сосуда 125 см2. Атмосферное давление 105 Па. Тепловым расширением сосуда и поршня пренебречь. (Решение)
2008 год. 5941 вариант. С2
В калориметре находился m1 = 1 кг льда при температуре t1 = -5°С. После добавления в калориметр m2 = 25 г воды в нем установилось тепловое равновесие при температуре t = 0°С. Какова температура t2 добавленной в калориметр воды, если в калориметре оказался в итоге только лёд? Теплоёмкостью калориметра пренебречь. (Решение)
2008 год. 05205939 вариант. С2
В горизонтально расположенной трубке постоянного сечения, запаянной с одного конца, помещен столбик ртути длиной 15 см, который отделяет воздух в трубке от атмосферы. Трубку расположили вертикально запаянным концом вниз. На сколько градусов следует нагреть воздух в трубке, чтобы объём, занимаемый воздухом, стал прежним? Температура воздуха в лаборатории 300 К, а атмосферное давление составляет 750 мм рт.ст. (Решение)
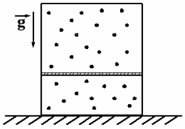 2008 год. 2 вариант. С2
2008 год. 2 вариант. С2
Вертикально расположенный замкнутый цилиндрический сосуд высотой 50 см разделен подвижным поршнем весом 110 Н на две части, в каждой из которых содержится одинаковое количество водорода при температуре 361 К. Какая масса газа находится в каждой части цилиндра, если поршень находится на высоте 20 см от дна сосуда? Толщиной поршня пренебречь. (Решение)
2007 год. 19 вариант. С2
В сосуде находится одноатомный идеальный газ, масса которого 12 г, а молярная масса 0,004 кг/моль. Вначале давление в сосуде было равно 4•105 Па при температуре 400 К. После охлаждения газа давление понизилось до 2•105 Па. Какое количество теплоты отдал газ? (Решение)
2006 год. 61 вариант. С2
В водонепроницаемый мешок, лежащий на дне моря на глубине 73,1 м, закачивается сверху воздух. Вода вытесняется из мешка через нижнее отверстие, и когда объём воздуха в мешке достигает 28,0 м3- мешок всплывает вместе с прикреплённым к нему грузом. Масса оболочки мешка 2710 кг. Определите массу груза. Температура воды равна 7°С, атмосферное давление на уровне моря равно 105 Па. Объёмом груза и стенок мешка пренебречь. (Решение)
2006 год. 86 вариант. С2
Теплоизолированный сосуд объемом V = 2 м3 разделен теплоизолирующей перегородкой на две равные части. В одной части сосуда находится 2 моль гелия, а в другой – такое же количество молей аргона. Начальная температура гелия равна 300 К, а температура аргона 600 К. Определите давление смеси после удаления перегородки. Теплоемкостью сосуда пренебречь. (Решение)
2006 год. 33 вариант. С2
Воздушный шар объемом 2500 м3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Температура окружающего воздуха 7°С, его плотность 1,2 кг/м3. При какой минимальной разности температур воздуха внутри шара и снаружи шар взлетит вместе с грузом (корзиной и воздухоплавателем) массой 200 кг? Оболочку шара считать нерастяжимой. (Решение)
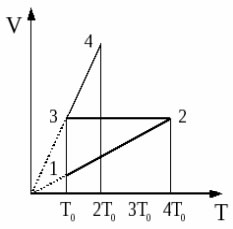
2006 год. 222 вариант. С2
С одним молем идеального одноатомного газа совершают процесс 1-2-3-4, показанный на рисунке в координатах V-Т. Во сколько раз количество теплоты, полученное газом в процессе 1-2-3-4, больше работы газа в этом процессе? (Решение)
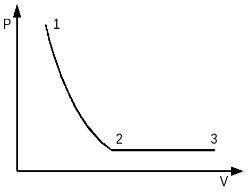 2005 год. 58 вариант. С2
2005 год. 58 вариант. С2
Идеальный одноатомный газ в количестве 1 моль сначала изотермически расширился при температуре T1 = 300 К. Затем газ изобарно нагрели, повысив температуру в 3 раза. Какое количество теплоты получил газ на участке 2-3? (Решение)
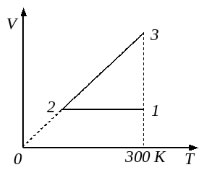
2004 год. 92 вариант. С2
10 моль одноатомного идеального газа сначала охладили, уменьшив давление в 3 раза, а затем нагрели до первоначальной температуры 300 К (см. рисунок). Какое количество теплоты получил газ на участке 2-3? (Решение)
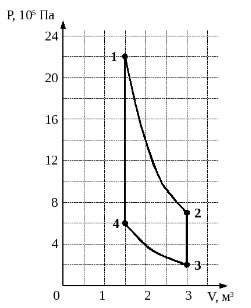 2004 год. 77 вариант. С5
2004 год. 77 вариант. С5
Идеальный одноатомный газ используется в качестве рабочего тела в тепловом двигателе. В ходе работы двигателя состояние газа изменяется в соответствии с циклом, состоящим из двух адиабат и двух изохор (см. рисунок). Вычислите КПД такого двигателя. (Решение)
2004 год. 49 вариант. С5
При электролизе воды образуется кислород О2 и водород Н2. Газы отводят в сосуд объёмом 100 л, поддерживая в нём температуру 300 К. Чему равна масса воды, которая разложилась в результате электролиза, чтобы суммарное давление в сосуде достигло 0,1 атм? Считать, что ничего не взрывается.
(Решение)
2004 год. 35 вариант. С5
Смесь одинаковых масс гелия, водорода и азота помещена в сосуд и нагрета до температуры 350 К. Плотность смеси оказалась равной 50 г/м3. Чему равно давление в сосуде? (Решение)
Источник
Автор
Тема: Основы МКТ. Идеальный газ из сборника задач Савченко Н.Е. (Прочитано 39169 раз)
0 Пользователей и 1 Гость просматривают эту тему.
422. Два сосуда, содержащих один и тот же газ при одинаковой температуре, соединены трубкой с краном. Вместимости сосудов V1 и V2, а давления в них р1 и p2. Каким будет давление газа после того, как откроют кран соединительной трубки? Температуру газа считать постоянной.
Решение. После того как откроют кран, каждый из газов станет занимать объем V = V1 + V2, а давления их уменьшаться и станут равными p3 и p4. Общее давление двух газов будет равно
p = p3 + p4. (1)
Так как «температуру газа считать постоянной», то для каждого газа считаем процесс изотермическим:
p1⋅V1 = p3⋅(V1 + V2), (2)
p2⋅V2 = p4⋅(V1 + V2). (3)
Решим систему уравнений (1)-(3). Например,
[ p_{3} =frac{p_{1} cdot V_{1}}{V_{1} +V_{2}}, ;;; p_{4} =frac{p_{2} cdot V_{2} }{V_{1} +V_{2}}, ;;; p=frac{p_{1} cdot V_{1} +p_{2} cdot V_{2} }{V_{1} +V_{2}}. ]
Записан
423. В расположенные вертикально сообщающиеся цилиндрические сосуды, первый из которых имеет площадь поперечного сечения S1, а второй S2, налили жидкость. Затем первый сосуд закрыли и находящийся в нем воздух нагрели от температуры T1 до температуры Т2, в результате чего уровень жидкости во втором сосуде поднялся на величину h. Определить температуру Τ2, если известно, что начальный объем воздуха в закрытом сосуде V1, атмосферное давление p0, плотность жидкости ρ. Тепловым расширением сосуда и жидкости пренебречь.
Решение. Для сообщающихся сосудов выполняются условие равновесия жидкости (в однородной жидкости на одном уровне гидростатические давления равны) (рис. 1):
рА = рВ,
где pА = p2, pВ = ρ⋅g⋅h2 + p0. Тогда
p2 = ρ⋅g⋅h2 + p0. (1)
Из рисунка 1 видно, что
h2 = Δh1 + h,
где Δh1 — высота, на которую опустится жидкость в закрытом сосуде.
Из условия не сжимаемости жидкости
ΔV1 = ΔV2, S1⋅Δh1 = S2⋅h.
Тогда
[ Delta h_{1} =frac{S_{2}}{S_{1} } cdot h, ; ; ; h_{2} =frac{S_{2}}{S_{1}} cdot h+h =left(frac{S_{2} }{S_{1} } +1right)cdot h. ;;; (2) ]
Давление p2 найдем из уравнения Клапейрона для воздуха в закрытом сосуде:
[ frac{p_{1} cdot V_{1} }{T_{1} } =frac{p_{2} cdot V_{2} }{T_{2} }, ;;; (3) ]
где p1 = p0, V2 = V1 + S1⋅Δh1 = V1 + S⋅h.
Решим систему уравнений (1)-(3). Например,
[ p_{2} =rho cdot gcdot left(frac{S_{2}}{S_{1} } +1right)cdot h+p_{0}, ; ; ; T_{2} =p_{2} cdot V_{2} cdot frac{T_{1}}{p_{1} cdot V_{1}} = ]
[ =left(rho cdot gcdot left(frac{S_{2}}{S_{1}} +1right)cdot h+p_{0} right)cdot left(V_{1} +S_{2} cdot hright)cdot frac{T_{1} }{p_{0} cdot V_{1}}. ]
Записан
424. Воздух находится в открытом сверху вертикальном цилиндрическом сосуде под поршнем массой m = 20 кг с площадью поперечного сечения S = 20 см2. После того как сосуд стали двигать вертикально вверх с ускорением a = 5,0 м/с2, высота столба воздуха между поршнем и дном сосуда уменьшилась и стала составлять α = 0,80 начальной высоты. Считая температуру постоянной, найти по этим данным атмосферное давление. Трением между поршнем и стенками сосуда пренебречь.
Решение. В задаче описано два состояния воздуха под поршнем: 1) сосуд неподвижен; 2) сосуд движется вверх с ускорением.
На поршень в двух случаях действуют сила тяжести (m⋅g), сила атмосферного давления (F0) и сила давления воздуха под поршнем (F), где F0 = p0⋅S, F = p⋅S, p0 — атмосферное давление, p — давление воздуха под поршнем. Запишем проекцию второго закона Ньютона для двух состояний:
1 состояние (рис. 1)
Y: F1 – F0 – m⋅g = 0
или
p1⋅S – p0⋅S – m⋅g = 0, (1)
2 состояние (рис. 2)
Y: F2 – F0 – m⋅g = m⋅a
или
p2⋅S – p0⋅S – m⋅g = m⋅a. (2)
Так как температура постоянна, то для воздуха под поршнем процесс изотермический. Поэтому
p1⋅V1 = p2⋅V2,
где V1 = S⋅l1, V2 = S⋅l2, l2 = α⋅l1 (по условию). Тогда
p1⋅S⋅l1 = p2⋅S⋅α⋅l1 или p1 = α⋅p2. (3)
Решим систему уравнений (1)-(3). Например,
p2⋅S = m⋅a + p0⋅S + m⋅g,
α⋅p2⋅S – p0⋅S – m⋅g = 0, α⋅(m⋅a + p0⋅S + m⋅g) – p0⋅S – m⋅g = 0,
p0⋅S⋅(1 – α) = α⋅m⋅a – m⋅g⋅(1 – α),
[ p_{0} =frac{alpha cdot mcdot a}{Scdot left(1-alpha right)} -frac{mcdot g}{S} =left(frac{alpha cdot a}{1-alpha } -gright)cdot frac{m}{S}, ]
p0 = 1,0⋅105 Па.
Записан
430. Определить давление насыщенного водяного пара при температуре t = 17 °С, если в комнате вместимостью V = 50 м3 при относительной влажности φ = 65 % и указанной температуре находится m = 0,476 кг паров воды. Универсальная газовая постоянная R = 8,31 Дж/(моль⋅К), молярная масса воды Μ = 18⋅10–3 кг/моль.
Решение. Используя уравнение Клапейрона-Менделеева, найдем давление пара
[ pcdot V=frac{m}{M} cdot Rcdot T, ; ; ; p=frac{mcdot Rcdot T}{Mcdot V}. ]
Тогда давление насыщенного пара pn найдем так (φ = 0,65):
[ varphi =frac{p}{p_{n} }, ; ; ; p_{n} =frac{mcdot Rcdot T}{Mcdot Vcdot varphi }, ]
pn = 1,96⋅103 Па.
« Последнее редактирование: 05 Октября 2011, 08:31 от alsak »
Записан
431. Смешали V1 = 1,0 м3 воздуха с относительной влажностью φ1 = 20 % и V2 = 2,0 м3 воздуха с влажностью φ2 = 30 %. Обе порции были взяты при одинаковых температурах. Определить относительную влажность получившейся смеси.
Решение. При смешивании разных порций воздуха при одинаковой температуре, получим воздух при той же температуре. Следовательно, давление pn и плотность ρn насыщенного пара воздуха не изменится.
Запишем уравнения для влажности для трех порций воздуха через плотности (φ1 = 0,20, φ2 = 0,30)
[ varphi _{1} =frac{rho _{1} }{rho _{n}}, ; ; ; varphi _{2} =frac{rho _{2} }{rho _{n} }, ; ; ; varphi _{3} =frac{rho _{3} }{rho _{n} }, ]
где плотности пара равны соответственно:
[ rho _{1} =frac{m_{1} }{V_{1} }, ; ; ; rho _{2} =frac{m_{2} }{V_{2} }, ; ; ; rho _{3} =frac{m_{1} +m_{2} }{V_{1} +V_{2}}. ]
Тогда
[ rho _{1} =varphi _{1} cdot rho _{n}, ; ; ; m_{1} =rho _{1} cdot V_{1} =varphi _{1} cdot rho _{n} cdot V_{1}, ; ; ; m_{2} =rho _{2} cdot V_{2} =varphi _{2} cdot rho _{n} cdot V_{2}, ]
[ rho _{3} =frac{left(varphi _{1} cdot V_{1} +varphi _{2} cdot V_{2} right)cdot rho _{n}}{V_{1} +V_{2}}, ; ; ; varphi _{3} =frac{varphi _{1} cdot V_{1} +varphi _{2} cdot V_{2} }{V_{1} +V_{2}}, ]
φ3 = 0,27 = 27 %.
Записан
425. По газопроводу течет газ при давлении p = 0,83 МПа и температуре Τ = 300 К. Какова скорость газа в трубе, если за время τ = 2,5 мин через поперечное сечение трубы площадью S = 5,0 см2 протекает m = 20 кг газа? Универсальная газовая постоянная R = 8,31 Дж/(моль⋅К), молярная масса газа Μ = 40⋅10–3 кг/моль.
Решение. Пусть υ — это скорость газа в трубе, тогда объем газа за время τ будет равен:
V = S⋅υ⋅τ.
Используя уравнение Клапейрона-Менделеева, найдем объем газа V:
[ pcdot V=nu cdot Rcdot T=frac{m}{M} cdot Rcdot T, ;;; V=frac{m}{Mcdot p} cdot Rcdot T. ]
Тогда
[ frac{m}{Mcdot p} cdot Rcdot T=Scdot upsilon cdot tau , ; ; ; upsilon =frac{mcdot Rcdot T}{Mcdot pcdot Scdot tau }, ]
υ = 20 м/с.
Записан
426. Относительная влажность воздуха в помещении φ = 63%, температура t1 = 18 °С. До какой температуры надо охладить блестящий предмет, чтобы на его поверхности можно было наблюдать осаждение водяных паров? Давление насыщенного водяного пара при 18 °С равно 20,7⋅102 Па, при 10 °С — 12,3⋅102 Па, при 11 °С — 13,1⋅102 Па.
Решение. На блестящей поверхности предмета можно будет наблюдать осаждение водяных паров, если пар у поверхности станет насыщенным.
Найдем давление водяных паров при температуре 18 °С при помощи следующей формулы:
[ varphi =frac{p}{p_{n}}, ]
где φ = 0,63, pn = 20,7⋅102 Па — давление насыщенного пара при температуре 18 °C. Тогда
p = pn⋅φ,
p = 1,30⋅103 Па. С таким давлением пар становится насыщенным при температуре меньше 11 °С.
Записан
427. Воздух в помещении имеет температуру t1 = 24 °С и относительную влажность φ1 = 50 %. Определить влажность воздуха после его охлаждения до t2 = 20 °С. Процесс охлаждения считать изохорным. Давление насыщенного водяного пара при 24 и 20 °С — соответственно p01 = 2943 Па и p02 = 2330 Па.
Решение. В задаче описано два состояния газа. Запишем уравнения для расчета относительной влажности для воздуха при температуре t1 = 24 °С и t2 = 20 °С:
[ varphi _{1} =frac{p_{1}}{p_{01}}, ;;; (1) ;;; varphi _{2} = frac{p_{2}}{p_{02}}, ;;; (2) ]
где φ1 = 0,50. По условию процесс охлаждения изохорный, т.е.
[ frac{p_{1} }{T_{1} } =frac{p_{2} }{T_{2} }. ;;; (3) ]
Решим систему уравнений (1)-(3). Например,
[ frac{p_{1}}{p_{2}} =frac{T_{1}}{T_{2}}, ;;; frac{varphi _{1}}{varphi _{2}} =frac{p_{1}}{p_{2}} cdot frac{p_{02}}{p_{01}} =frac{T_{1}}{T_{2}} cdot frac{p_{02}}{p_{01}}, ;;; varphi _{2} =varphi _{1} cdot frac{p_{01} cdot T_{2}}{p_{02} cdot T_{1}}, ]
φ2 = 0,62 = 62 %.
Записан
428. Над поверхностью площадью S = 5,0 км2 слой воздуха толщиной h = 1000 м имеет температуру t1 = 20 °С при относительной влажности φ = 73 %. Воздух охладился до температуры t2 = 10 °С. Найти массу выпавшего дождя. Плотность насыщенного водяного пара при температурах t1 и t2 — соответственно ρ01 = 17,3⋅10–3 кг/м3 и ρ02 = 9,4⋅10–3 кг/м3.
Решение. Найдем плотность пара при температуре t1 = 20 °С и влажности φ:
[ varphi =frac{rho _{1}}{rho _{01}}, ;;; rho _{1} = phi cdot rho _{01}, ]
где φ = 0,73. Тогда ρ1 = 12,6⋅10–3 кг/м3. Тогда масса пара равна
m1 = ρ1⋅V = ρ1⋅S⋅h = φ⋅ρ01⋅S⋅h. (1)
Плотность ρ1 больше плотности насыщенного пара ρ02 при температуре t2 = 10 °С. Следовательно, пар при температуре t2 станет насыщенным и его плотность будет равна ρ02. Тогда масса пара равна
m2 = ρ02⋅V = ρ02⋅S⋅h. (2)
Масса выпавшего дождя, с учетом уравнений (1) и (2), равна:
Δm = m1 – m2 = (φ⋅ρ01 – ρ02)⋅S⋅h,
Δm = 1,6⋅107 кг.
Записан
429. Калорифер подает в помещение V = 5,0⋅104 м3 воздуха при температуре t1 и относительной влажности φ1 = 60 %, забирая его с улицы при температуре t2 и относительной влажности φ2 = 80 %. Сколько воды дополнительно испаряет калорифер в подаваемый воздух? При температуре t1 плотность насыщенного водяного пара ρ01 = 15,4⋅10–3 кг/м3, а при температуре t2 — ρ02 = 9.4⋅10–3 кг/м3.
Решение. Масса воды, которую нужно дополнительно испарить в каждый кубометр воздуха Δm = m1 – m2, где m1 и m2 — массы водяных паров при температурах t1 и t2 соответственно. Масса водяных паров в воздухе равна
m = ρ⋅V,
где плотность ρ найдем через относительную влажность
[ varphi =frac{rho }{rho _{0}}, ;;; rho =varphi cdot rho _{0}. ]
Тогда массы паров при температурах t1 и t2 будут равны
m1 = ρ1⋅V = φ1⋅ρ01⋅V, m2 = ρ2⋅V = φ2⋅ρ02⋅V,
где φ1 = 0,60, φ2 = 0,80. В итоге получаем
Δm = (φ1⋅ρ01 – φ2⋅ρ02)⋅V,
Δm = 86 кг.
Записан
Источник