В вертикально расположенном сосуде находится масло
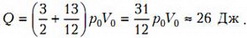
Можаев В. Задачи с жидкостями //Квант. — 2006. — № 1. — С. 40-43.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
В этой статье будут рассмотрены задачи, в которых жидкость, с одной стороны, является средой, где находятся твердые тела, а с другой стороны, она, как жидкий элемент, участвует в движении, подобно твердому телу. Наиболее сложными являются комбинированные задачи, в которых жидкость движется вместе с находящимся в ней твердым телом (например, разобранная ниже задача 6).
Перейдем к обсуждению конкретных задач.
Задача 1. В цилиндрический сосуд с водой опустили кусок льда, в который вморожен осколок стекла. При этом уровень воды в сосуде поднялся на h = 11 мм, а лед остался на плаву, целиком погрузившись в воду. На сколько опустится уровень воды в сосуде после того, как весь лед растает? Плотность воды ρв = 1 г/см3, плотность льда ρл = 0,9 г/см3, стекла ρст = 2,0 г/см3
Обозначим первоначальный объем льда через Vл, а объем стекла — через Vст. Когда кусок льда полностью погрузился в воду, он вытеснил объем воды, равный
Очевидно, что этот же объем равен
где S — площадь поперечного сечения сосуда.
Теперь запишем условие плавания куска льда с вмороженным осколком стекла — суммарная сила тяжести льда и стекла равна выталкивающей силе:
Из совместного решения полученных уравнений найдем объемы льда и стекла:
Из растаявшего льда образовалась вода объемом
Поскольку кусок стекла остается в воде, понижение уровня воды в сосуде за время таяния льда будет равно
Задача 2. В вертикально расположенной трубке — с открытым верхним концом, с постоянным внутренним сечением и длиной 3L = 1080 мм — столбиком ртути длиной L заперт слой воздуха такой же длины. Какой длины столб ртути останется в трубке, если ее перевернуть открытым концом вниз? Внешнее давление p0 = 774 мм рт. ст.
Обозначим давление воздуха под ртутным столбиком в исходном положении трубки через p1. Тогда условие равновесия столбика ртути длиной L запишется в виде
где ρ – плотность ртути. Предположим, что после переворота трубки и установления первоначальной температуры часть ртути выльется. Обозначим через h длину столбика оставшейся в трубке ртути. Новое условие равновесия будет иметь вид
где p2 – новое давление воздуха над ртутным столбиком.
Условие сохранения количества изолированного воздуха позволяет записать
Подставляя сюда p1 из первого равенства, а p2 – из второго, получим уравнение относительно h:
или, если записать атмосферное давление в виде , где H0 = 774 мм:
Для данных численных значений L и H0 (в мм) получается, что
h = 270 мм.
Задача 3. U–образная трубка расположена вертикально и заполнена жидкостью. Один конец трубки открыт в атмосферу, а другой конец соединен с сосудом объемом V0 = 0,1 л, заполненным гелием (рис. 1). Объем всей трубки равен объему этого сосуда. В некоторый момент гелий начинают медленно нагревать. Какое минимальное количество теплоты необходимо подвести к гелию, чтобы вся жидкость вылилась из трубки? Атмосферное давление p0 = 105 Па; длины трех колен трубки одинаковы; давление, создаваемое столбом жидкости в вертикальном колене, равно p0/8.
Рис. 1
Обозначим полную длину трубки через 3L, а площадь внутреннего поперечного сечения трубки – S. Поскольку объем трубки V0, то длина каждого колена
Весь процесс нагрева гелия можно разбить на три участка. Первый участок — это когда жидкость еще находится в левом вертикальном колене. Рассмотрим момент времени, когда уровень жидкости в левом колене переместился на величину z, . Из условия равновесия жидкости в трубке найдем давление гелия:
где ρж – плотность жидкости. На втором участке, для которого , давление гелия
а на третьем участке, для
На рисунке 2 изображен график зависимости давления гелия от его объема V, который связан со смещением z простым соотношением:
На первых двух участках тепло необходимо подводить к гелию — это однозначно: здесь газ, расширяясь, совершает работу и одновременно нагревается. А вот третий участок неоднозначен: здесь газ также совершает работу, но при этом он может и охлаждаться. Убедимся, что и на этом участке тепло тоже подводится.
Учитывая, что , запишем уравнение процесса для третьего участка в виде
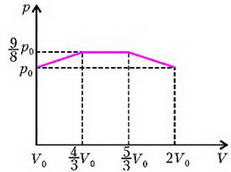
Рис. 2.
Рассмотрим малое изменение объема ΔV. Тогда работа, совершенная гелием, равна
Запишем уравнение состояния гелия как идеального газа:
где ν – количество вещества, Т – температура газа. Подставим в это уравнение выражение для давления на третьем участке процесса и получим
Продифференцируем обе части этого уравнения:
Теперь найдем изменение внутренней энергии гелия при изменении объема на ΔV:
Согласно первому началу термодинамики, подведенное количество теплоты равно сумме изменения внутренней энергии газа и совершенной им работы:
Легко убедиться, что при и
Итак, на всех участках тепло подводится, поэтому полное подведенное к гелию количество теплоты Q найдем как сумму полного изменения внутренней энергии и полной работы, которую совершил гелий:
Поскольку начальная и конечная температуры равны, соответственно,
то изменение внутренней энергии равно
Полную работу найдем как площадь под кривой на рисунке 2:
Тогда окончательно
Задача 4. «Тройник» с двумя открытыми в атмосферу вертикальными трубками и одной закрытой (горизонтальная трубка) полностью заполнен водой (рис. 3). После того, как тройник начали двигать по горизонтали в плоскости рисунка влево с некоторым постоянным ускорением, из него вылилась 1/16 массы всей воды. Чему при этом стало равно давление в жидкости у закрытого конца – в точке А? Трубки имеют одинаковые внутренние сечения. Длину L считать заданной. Диаметр трубок мал по сравнению с длиной L.
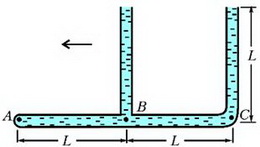
Рис. 3.
При движении тройника влево с ускорением а гидростатические давления в точках А, В и С (см. рис. 3) связаны между собой уравнением движения воды в горизонтальной трубке:
где ρ – плотность воды. Давление в точке С больше давления в точке В, поэтому вода будет выливаться из правой вертикальной трубки. Из условия неразрывности струи жидкость при этом будет отсасываться из левой вертикальной трубки. В установившемся режиме правая трубка будет полностью заполнена водой, а левая – частично. Поскольку вылилась 1/16 массы всей воды, что соответствует массе воды в части трубки длиной L/4, то в левой трубке останется столбик воды высотой 3/4L. Поэтому давления в точках В и С будут равны
где p0 – атмосферное давление.
Исключая из всех уравнений рB и рС, получим систему двух уравнений относительно рА и а:
Решая эту систему относительно рА, найдем
Задача 5. Тонкая, запаянная с одного конца и изогнутая под прямым углом трубка заполнена ртутью и закреплена на горизонтальной платформе, которая вращается с угловой скоростью ω вокруг вертикальной оси (рис. 4). При вращении платформы ртуть не выливается и полностью заполняет горизонтальное колено. Открытое колено трубки вертикально. Геометрические размеры установки указаны на рисунке; атмосферное давление р0; плотность ртути ρ. Найдите давление ртути у запаянного конца трубки.
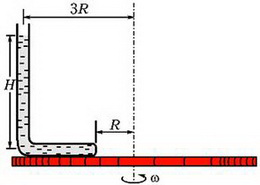
Рис. 4.
Выделим в горизонтальной части трубки небольшой элемент ртути длиной dr, расположенный на произвольном расстоянии r от оси вращения (рис. 5).
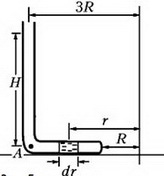
Рис. 5.
Этот элемент вращается в горизонтальной плоскости с угловой скоростью ω. Запишем уравнение движения выделенного элемента:
где S – площадь поперечного сечения трубки, dp – разность давлений между левым концом элемента ртути и правым. После сокращения на S получим связь между малыми приращениями dp и dr:
Проинтегрируем обе части этого уравнения и получим
Константу определим из условия, что при r = 3R (точка А) давление равно
и получим зависимость p(r)
Отсюда найдем давление ртути у запаянного конца трубки (r = R):
Задача 6. Стеклянный шар объемом V и плотностью ρ находится в сосуде с водой (рис. 6). Угол между стенкой сосуда и горизонтальным дном α, внутренняя поверхность сосуда гладкая, плотность воды ρ0. Найдите силу давления шара на дно сосуда в двух случаях: 1) сосуд неподвижен; 2) сосуд движется с постоянным горизонтальным ускорением а.
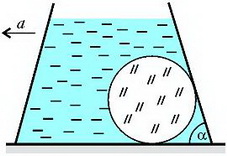
Рис. 6.
Сначала рассмотрим движущийся по горизонтали с постоянным ускорением а сосуд с водой. Введем систему координат XY, связанную с сосудом, как это изображено на рисунке 7.
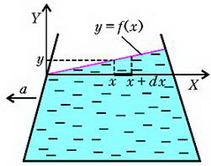
Рис. 7.
Наша задача – найти уравнение свободной поверхности жидкости в сосуде, который движется с горизонтальным ускорением а. Для этого выделим маленький элемент жидкости на оси Х, длина которого dx, а площадь поперечного сечения равна единице. С левого торца этого элемента давление равно
а с правого торца оно равно
где у – высота столба жидкости в точке х, а – аналогичная высота в точке . Так как наш элемент жидкости движется с ускорением а, его уравнение движения имеет вид
Отсюда получаем
или в интегральном виде —
Поскольку при х = 0 у = 0, константа тоже равна нулю, а уравнение свободной поверхности жидкости выглядит так:
Линии, параллельные свободной поверхности, внутри жидкости являются линиями постоянного давления. Таким образом, жидкость, движущаяся с горизонтальным ускорением а, эквивалентна неподвижной жидкости, находящейся в новом поле тяжести с эффективным «ускорением свободного падения», равным и направленным под углом к вертикали (рис. 8). Вертикальная составляющая этого эффективного ускорения равна обычному ускорению свободного падения g, а горизонтальная составляющая численно равна ускорению сосуда и направлена в противоположную сторону.
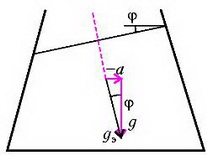
Рис. 8.
В том случае, когда сосуд неподвижен (а = 0), эффективное ускорение равно g и направлено по вертикали. Силы, действующие на стеклянный шар в этом случае, показаны на рисунке 9.
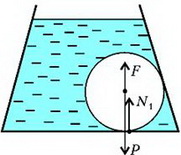
Рис. 9.
Здесь – вес (точнее – сила тяжести) шара, – выталкивающая сила, а N1 – сила реакции дна сосуда на шар. Из условия равновесия шара найдем, что
Очевидно, что сила давления шара на дно численно равна силе реакции дна и направлена в противоположную сторону.
В случае движущейся с горизонтальным ускорением a жидкости или неподвижной жидкости, но находящейся в поле с новым «ускорением свободного падения» gЭ, на шар будут действовать следующие силы (рис.10): вертикальная составляющая нового веса шара , горизонтальная составляющая этого веса , вертикальная составляющая выталкивающей силы , ее горизонтальная составляющая , реакция опоры Т со стороны боковой стенки и, наконец, сила N2 – сила реакции на шар со стороны дна сосуда. Запишем условие равновесия шара, т.е. равенство нулю всех сил, действующих на шар по вертикали:
и по горизонтали:
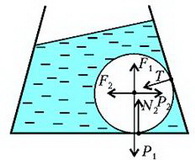
Рис. 10.
Исключая из этих уравнений Т, найдем искомую силу N2:
Разумеется, и в этом случае сила давления шара на дно сосуда численно равна силе реакции дна, но направлена в противоположную сторону.
Упражнения.
1. В цилиндрическом сосуде с водой плавает деревянная дощечка. Если на нее сверху положить стеклянную пластинку, то дощечка с пластинкой останутся на плаву, а уровень воды в сосуде повысится на Δh1. На сколько изменится уровень воды в сосуде с плавающей дощечкой, если ту же стеклянную пластинку бросить на дно сосуда? Плотность стекла ρст, плотность воды ρв.
2. U–образная трубка состоит из трех одинаковых колен, расположена вертикально и заполнена жидкостью (см. рис. 1). Один конец трубки соединен с баллоном, заполненным водородом, другой конец открыт в атмосферу. Водород в баллоне медленно нагревают, и он постепенно вытесняет жидкость из трубки. К моменту, когда из трубки вылилось 2/3 всей массы жидкости, водород получил количество теплоты Q = 30 Дж. Найдите объем баллона. Известно, что объем всей трубки равен объему баллона; атмосферное давление p0 = 105 Па; давление, создаваемое столбом жидкости в вертикальном колене трубки, равно p0/9.
3. «Тройник» из трех вертикальных открытых в атмосферу трубок полностью заполнен водой (рис. 11). После того, как тройник начали двигать в горизонтальном направлении в плоскости рисунка с некоторым ускорением, из него вылилось 9/32 всей массы воды. Чему равно ускорение тройника? Внутренние сечения трубок одинаковы, длина каждой трубки L.
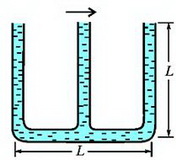
Рис. 11
4. Тонкая, запаянная с одного конца и изогнутая под прямым углом трубка заполнена жидкостью и закреплена на горизонтальной платформе, вращающейся с угловой скоростью ω вокруг вертикальной оси (рис. 12). Открытое колено трубки вертикально. Геометрические размеры установки указаны на рисунке; атмосферное давление p0; плотность жидкости ρ. Найдите давление жидкости у запаянного конца трубки.
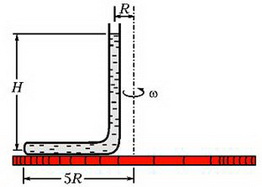
Рис. 12
Ответы.
1.
2.
3. .
4.
Источник
А. увеличивается среднее расстояние между его молекулами.
Б. молекулы почти перестают притягиваться друг к другу.
В. полностью теряется упорядоченность в расположении его молекул.
1) только А 3) только В
2) только Б 4) А, Б и В
20(В) Определите давление газа при температуре 127 оС, если концентрация молекул в нем 1021 частиц на 1 м3. Ответ выразите в паскалях и округлите до целых.
21(В) В сосуде объемом 110 л находится 0,8кг водорода и 1,6 кг кислорода. Определите давление смеси, если температура окружающей среды 27 оС.
22(В) В 1 см3 объема при давлении 20 кПа находится 5·1019 молекул гелия. Определите среднюю квадратичную скорость молекул при этих условиях.
23(В) Идеальный одноатомный газ в количестве ν = 0,09 моль находится в равновесии в вертикальном цилиндре под поршнем массой m = 5 кг. Трение между поршнем и стенками цилиндра отсутствует. Внешнее атмосферное давление равно pо=105 Па. В результате нагревания газа поршень поднялся на высоту Δh = 4 см, а температура газа поднялась на ΔТ = 16 К. Чему равна площадь поршня? Ответ выразите в см2 и округлите до целых.
24(С) В сосуде находятся жидкость и ее насыщенный пар. В процессе изотермического расширения объем, занимаемый паром, увеличивается в 3 раза, а давление пара уменьшается в 2 раза. Найдите отношение массы m2 жидкости к массе m1 пара, которые первоначально содержались в сосуде.
25(С) В вертикально расположенном закрытом цилиндрическом сосуде, разделенным поршнем массы m = 0,5 кг на два отсека, находится идеальный газ. Количество вещества в верхнем отсеке в 4 раза меньше, чем в нижнем. Площадь основания цилиндра S равна 20 см2. В положении равновесия поршень находится посередине сосуда. А температура в обоих отсеках одинаковая. Определите давление газа р в нижнем сосуде.
Ответы к тренировочным заданиям.
1А | 2А | 3А | 4А | 5А | 6А | 7А | 8А | 9А | 10А | 11А | 12А | 13А | 14А | 15А | 16А |
4 | 1 | 3 | 3 | 4 | 2 | 1 | 1 | 2 | 3 | 4 | 4 | 3 | 4 | 1 | 3 |
17А | 18А | 19А | 20В | 21В | 22В | 23В | 24С | 25С | |||||||
3 | 3 | 4 | 6 Па | 10,2 МПа | 425 м/с | 25 см2 | 0,5 | 3300 Па |
24С При изотермическом увеличении объема жидкость начинает испаряться. Давление пара при этом не изменяется до тех пор, пока вся жидкость не испариться (пар остается насыщенным, и его давление определяется температурой). Дальнейшее увеличение объема вызывает уменьшение давления по закону Бойля-Мариотта. Пусть ,,;,, – начальное и конечное давление пара, его объем и температура. Уравнения состояния при этом имеют вид: , .
По условию /=3, /=2. Разделив уравнения, находим , .
25С Условие равновесия поршня: , где m – масса поршня; – сила давления на поршень газа, находящегося в верхнем отсеке; – сила давления на поршень газа, находящегося в нижнем отсеке. Силы давления рассчитываются по формулам , где р-давление газа; S-площадь поршня. Давление газа может быть определено из уравнения Менделеева – Клапейрона. По условию = , =, .
, , следовательно, отсюда
Контрольные задания.
1(А) Как зависит скорость диффузии от агрегатного состояния вещества при постоянной температуре?
1) не зависит
2) скорость максимальна в газах
3) скорость максимальна в жидкостях
4) скорость максимальна в твердых телах.
2(А) Скорость молекул газов воздуха имеет порядок…
1) 10-4 м/с– 103 м/с
2) 1 м/см/с
3(А) Как связаны между собой температура t по Цельсию и абсолютная температура T, измеряемая в кельвинах:
1) t = T + T = t
2) T = t + T = 273 – t
4(А) Молекулы газов находятся на больших расстояниях друг от друга по сравнению с их размерами, силы притяжения между ними незначительны. Этим можно объяснить следующие свойства газов:
А. Не имеют своей собственной формы.
Б. Не сохраняют своего объема.
В. Легко сжимаются.
Какие из утверждений правильны?
1) только А и Б 3) только Би В
2) только А и В 4) А, Б, В
5(А) Как изменится давление идеального газа на стенки сосуда, если в данном объеме средняя квадратичная скорость молекул удвоится, а концентрация молекул не изменится?
1) увеличится в 4 раза
2) увеличится в 2 раза
3) уменьшится в 4 раза
4) не изменится
6(А) В таблице представлен диаметр D пятна, наблюдаемого через промежуток времени t на мокрой пористой бумаге, лежащей на горизонтальном столе, после того как на нее капнул каплю концентрированного красителя.
t, ч | 1 | 2 | 4 | |
D, мм | 6 | 10 | 11,5 | 13,5 |
Какое явление стало причиной роста размеров пятна с течением времени?
1) растворение 3) распад красителя
2) диффузия 4) броуновское движение
7(А) На рисунке приведен
график зависимости
давления идеального
газа от температуры
при постоянном объеме.
Какой температуре соответствует точка А?
1) – 273 КоС
2) 0 К 4) 0 оС
8(А) Плотность железа примерно в 3 раза больше плотности алюминия. В алюминии количеством вещества 1 моль содержится атомов. В железе, количеством вещества 1 моль содержится атомов. Можно утверждать, что
1) =3 3)
2) = 4) = 6·1023
9(А) Какой из графиков,
изображженных на
рисунке, соответствует
процессу, проведенному
при постоянной
температуре газа?
1) А 2) Б 3) В 4) Г
10(А) Зависимость давления идеального газа р от температуры Т при постоянной плотности (см. рис.) представлена графиком…
11(А) Как соотносятся средние квадратичные скорости атомов кислорода кисл и водорода вод в смеси этих газов в состоянии теплового равновесия, если отношение молярных масс кислорода и водорода 16?
1) кисл = вод 3) кисл = 4вод
2) кисл = 16вод 4) кисл = вод
12(А) В баллоне объемом 1,66 м3 находится 2 кг азота при давлении 105 Па. Чему равна температура этого газа?
1) 280оСоС 3) 7оСоС
13(А) При температуре То и давлении ро один моль идеального газа занимает объем Vо. Каков объем этого же газа, взятого в количестве 2 моль, при давлении 2ро и температуре 2То?
1) 4Vо 2) 2Vо 3) Vо 4) 8Vо
14(А) При изобарном нагревании водорода массой 2 г, находившегося в начале процесса под давлением 83 кПа, его температура возросла от 200 К до 500 К. Его объем при этом
1) не изменился
2) увеличился на 0,03 м3
3) уменьшился в 2,5 раза
4) увеличился на 20 л
15(А) На рисунке показан
цикл, осуществляемый
идеальным газом. Изотер-
мическому расширению
соответствует участок
1) АВ 2) DА 3) СD 4) ВС
16(А) Из стеклянного сосуда выпускают сжатый газ, одновременно охлаждая сосуд. При этом температура газа снизилась в 4 раза, а его давление уменьшилось в 6 раз. Во сколько раз уменьшилась масса газа в сосуде? Газ можно считать идеальным.
1) в 2 раза 3) в 6 раз
2) в 3 раза 4) в 1,5 раза
17(А) Атомы в кристалле находятся друг от друга на таких расстояниях, при которых силы притяжения…
1)…больше сил отталкивания
2)…меньше сил отталкивания
3)… равны силам отталкивания
4)… равны нулю.
18(А) Ученик, наблюдая процесс испарения жидкости при комнатной температуре, заметил, что вода, налитая в блюдце, испарилась быстрее, чем вода такой же массы, налитая в чашку. Какой вывод он должен сделать из этого наблюдения?
1) Скорость испарения жидкости не зависит от ее температуры.
2) Скорость испарения жидкости зависит от площади ее поверхности.
3) Скорость испарения жидкости зависит от ее температуры.
4) Скорость испарения жидкости зависит от плотности водяного пара над поверхностью жидкости.
19(А) С уменьшением относительной влажности воздуха разность показаний термометров психрометра…
1) увеличивается
2) уменьшается
3) не изменяется
4) становится равной нулю.
20(А) Относительная влажность воздуха в комнате равна 25%. Каково соотношение парциального давления р водяного пара в комнате и давления рн насыщенного водяного пара при такой же температуре?
1) р меньше рн в 4 раза
2) р больше рн в 4 раза
3) р меньше рн на 25%
4) р больше рн на 25%
21(В) Идеальный газ, количество которого 1,5 моля, совершает
процесс a-b, изображен-
ный на графике. Чему
равна температура газа,
находящегося в состоянии, которому соответствует точка b? Ответ округлите до целого числа. Ответ выразите в К.
22(В) Температура воздуха в помещении объемом 60 м3 при нормальном атмосферном давлении равна 15 оС. После подогрева воздуха калорифером его температура поднялась до 20 оС. Найти массу воздуха, вытесненного из комнаты за время нагревания. Молярная масса воздуха М = 29·10-3 кг/моль. Ответ округлите до сотых.
23(В) В баллоне содержится газ при температуре 17 оС и давлении 1 МПа. На сколько изменится давление, когда температура понизится до – 23 оС?
24(С) Как изменится температура идеального газа, если увеличить его объем в 2 раза при осуществлении процесса, описываемого формулой pV2 = const?
25(C) Воздушный шар с газонепроницаемой оболочкой массой 400 кг заполнен гелием. На высоте, где температура воздуха 17 оС и давление 105 Па, шар может удерживать груз массой 225 кг. Какова масса гелия в оболочке шара? Считать, что оболочка шара не оказывает сопротивления изменению объема шара.
Ответы к контрольным заданиям.
1А | 2А | 3А | 4А | 5А | 6А | 7А | 8А | 9А | 10А | 11А | 12А | 13А | 14А | 15А |
2 | 3 | 3 | 1 | 2 | 2 | 2 | 2 | 3 | 4 | 1 | 3 | 2 | 2 | 2 |
16А | 17А | 18А | 19А | 20А | 21В | 22В | 23В | 24С | 25С | |||||
4 | 3 | 2 | 1 | 1 | 160 К | 1,24кг | Δр = 0,14 МПа | Уменьшится в 2 р | 100 кг |
24С
Решение.
, температура уменьшится в 2 раза.
25С Шар с грузом удерживается в равновесии при условии, что сумма сил, действующих на него, равна нулю:, где М и m – массы оболочки и груза, масса гелия, а сила Архимеда, действующая на шар. Из условия равновесия следует: .
Давление р гелия и его температура Т равны давлению и температуре окружающего воздуха. Следовательно, согласно уравнению Клапейрона-Менделеева,
и , где V – объем шара. Отсюда: ; ; .
Следовательно, . Ответ: 100кг.
Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 |
Источник
