В вертикально расположенном сосуде с сечениями
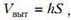
$m>²Gxg‡«˜ˆÛvXã¦ÛðÍ݇º’ï)c$ÌcCÝ”ã+šMRX¸‰ÝÆ¿2¼ö¼W´CÍå¶þ0}Üþ¬_ø&Zg6Àܬx%°}šå×5)N;=ú«’¸Ú8¦R(f äÆxüìL”˜)+dÄÊýPü>ÁÜ×iø…µ|-Ô-RWtS×U£bÒYNâBÉOª%Š_ÊS4må;¾f†1ø¹×NÓxÝz`”°|¸ršFZËó4pïDóq^ ÿ^ÓG³-…g¤ÅyZƒ«X}Û§Í溇I’çÿi”>ß:Δò´éÏ*Ç’~k«#w€’™œÜ8ÃôéÝî51M+Ó4·µØˆš˜Ï`ŽþJëçþÀNTåV‹ÃçY’œ!ûÅÌ@¼Uº MÜ!Žàè3è8é²$ÕÃAˆß{gœë9úü½% ÛbDšï|œŠªø©Öš6’m4æëÙ0ñ-0IÒÓaÈ àõ×·×FØ EÀ>ƒÓÌ}¤ÙÈ·x·oqµí,ñtÄ’fQ-·‡½¾}îTïÈãmE9 »í”{à(ZýábÈr·l~’ (hŸ>ˆ3* X©ú:?Lc¢Ë…bÔç÷Ëóa€mûÁbÎÛwpŠ=$óDž†ÆJÞp¯Ýß_3au…ém…Pß0½Ñ>Aªå¼Z/å¼,óÝË9¯Êméé×o4′}’ÐÙ˜¾(´¿-Cÿxµwi‹Ñæ%œ†!mÒj`J 1?»*ßshñÔ´)F{˜CñûÇ=>•xjEîø¦æ/™Ÿ’ ëZë‰)ŽÇ¦9`ÚwOûAZ˜]ùGÛ•ò,>yjžakÀ[‘ƒ÷c}HOÑ»q|wÝ·þû›ü’^DìÃOuE-×Áîc1?;Ùvóƒ9¨ÄýÔÛ½Ãj?xžÁsµÖóÖ˜b«.Ó$TFÇÐ(…ÜÀγ6üØþa2@ih?‰ÙLÎÄlvÒ¶¯Í~à¬ò£ÃŽ×Ú¿D&Þ*}U§|Q‹TÙÁF,ßázhˆ©Õ›EŒ`Ï6Z.y¯õï€6U}²ßR dê€ÜýOÌÁm§å¦Â~ŠpFñ¼¸|‰G3†ÔkÁŒ&u¾k[w”üZDTçKDoƒ”°ì™oËìmps°5bgãq:}½LÇát¿˜©`£ŒÁ¹ðºµ‰U ǯýâò%öõ0.õZr³vWƒHKý ;ùpÕ”1{C’¶ÇÓ+äP-ÙŠÎ’gůcXGl¹@ÿ§iMiÍ›{ÿ’ңǔBŽ˜Î¾³:zÀ-Ï/« Rê³hµ½’Ä*Ó:sµ3¥ýUá”R4Ÿèƒ -/®”æ»ûÁ¶Î2˜Ù0dÎËT¸:ÂLçGhIœg$9’FS9ïqRÙ¡ry”‰†Ú+|…rÁèÑvÞ2uÙKý¾aÖÔiW‡ÆVp`5õÜö>Îcvù½àÕ=jµ?”â6†ã‹qºnS¨Vì”Úî:|ÃÕä¦Ú4œ›”KJ¡-)RŽ,N‡Ù~ïTÇ×õÙä=X Ø(ÂTcXºÓ*-Y™2Ƚ夹´ùàE-Ñü1exÙèT K¦.‰÷l惻`•-º+OŽ”èGÞ-Å…ö$Œ0j£¾x1ñé¶ëŽî6XâÐÚA8²âz`ã§ÉÐ’ÊöèùÕû~ZÄ,6RÚÓ[tw=€²-0§]¶)Å:dfÊÙæa;gUX3Û9›®2ëë{8ÐÒ-ÔN×ÕVö]A?V…ö{ßqê6£º>Xµ éègþMëìig±ã•ïP•+*®±q5}£ã ]-†fñ4±
àOê- ÉQÌK±ÝÕê=#þ¶˜ûl½6Þqg|¯FóümˆwzR¨M’XÍlöû;þ’ëT˜¹fÀRÞIY z ÎÃHúß3·Ür’ûÞ¨ _fŠ rXBø«{¿ºhœnS‰óñ¢âAãÔ^Ú·ÊÇ’VXÉúä ‘´ç”õ]ÌÃÙÉaýÝò½º-‡r•*½Õs/d™š ß¿:«£ËuÛÉã=HºÁÛZÙ¹b¦¨sÏ6Ç£§³ÒõÜ?8-Á¯ôo_³¸¶*Zº/ls˜ÍÊ3ö»NæŽÎdïƒh$ë÷ÖýݘöÔ¾ Ú”~ŽEö®’í¼üÚ¾wdæ,2£êüuþ×M½aCÞøW›Ý†ÑñïÕ’å{þµ½Ý,ÖÚ°=¬ö´uxÁîbÂãâÊðÔõ3ƒ™³¦ËˆÆyÛ,Ì:cöwÆÙ”þx){ì7Ì]«¾fWÁê”ÕlÆ€š-džuèå›-`çÐÍaÞ¶£À½À§Ö§iï->·•ÝA†áž2éSF›»}òD¢¢uLùÿö1á+LSÒÇ0½ûaæ’Hµ¤Ï@륤¥u~¬ð·Y :¼_i’¼uŸcñ§ñãwk«ÇøXO×ãAõïì‡ èðŠ*[do5åÏÅš²[U°÷ÂxµVŸ)¼r”ã šU«‡ñ.ƒëQ‹ç’ÅéB”]ò÷¿ÚjŸ;-ð’£»Õž”¸ÿõ1(Ë«µÄ%NÆ¥?8lÉœÉáªß’±”í`Óo~¦»þâX5éÙÃ4jÆnqXËôü‹”ÐÏGU¥ a~œLU-ÉN‹C«î*,WJ)”Çä9|,ª”z>ßgJ”ä7žTïØõCºRˆ¥÷Ôƒ_û1sµ»ÚÜSª9>ÆCªD ?™³?
ò·*>°4 xÄãI{fRöÙ½µë (àtÿPË;ó’ìDQQ°T+y¢ ñÌÖüÞz lÄO }=`gãqf*U)Iy¸EnS#à ÇdE$ç^ˆÆyú·ûŠXÄ k(x±Ed?>£¡²Ü¼mg`¾3{™ÒLj£”œ€0’7í> “û¨p*Ú}˜òjH´1©Z¡a«i#»³Jc¿ËÒœƒ’¶còôLSZ#ÒÕÊÍtÍ’½o¯½óHšÞ»$nï}e/ÌM³®¿Y×Cë:éçpûA4Ù|ô”õfÊy qŸ(ºŒ¢|&¬kuŽ(hìf¿ó>QyfXäìÂïS8ùó( ~ú¤R…›”aˬÁaË-´õýEíaøÝë¶a¸Ý;Ƽૡ´”¤vö’ïÜm”è^é°Ý9AÑHE()½Ç”Ã~Kê0%Ÿ#®.{o4″¨ vkL3½;,…óýó¨Â°{4çQg@fõlŸÑP7Ÿˆû”ÞˆeÃcOõF ƒhé FôÁ”º !êhœï]¶z”û&/t äXÖO SùŸÑ%?ô(üÿ] ;†Q»È†èŽ”uFìyÈgÝà,¾iµa”ÆïgŒð·uÑõW¹õ e¿ý”Ö« l”iåÖÉ·vEc?n×]ª ؃@”è!àÊ$Ð]«uúž7¶Å”tc‡C7^ƒÇzˆmyƒ³,J¼ˆÚr+/Ü+ki¹¹¤¸šºV£n,ûË-õí¿éy›Êm’F7üþ¥]T8Á™öi¸[¶öý’€Ùë72Xxƒ¹éæ²ÑÀ ‘•1¼þqÙÛØýûÿúñ/îí·ÿ[©ý²-“0ÝŠ«>õµ#mDi-V8mòœW 1áAbé©’‹PBÂÂ0`êýã-ÁÝ:õñ”ŸjD¨Om7êï¿!ÀJm½|Z†þøDêHôóŸZœAõk¤.q£4Ý CÁ/! ÿFZü”à¿rtzÖçh^mÅy_â_Z±¡öq`ù»Ò?ˆCáŃ@&B]aÆùµPœ‡ Ã/üÛƒ!4Oþó+øÅ’F ×Çxè¶?Bé ¿E¿™C%¿õ-ˆ Åß•þù¹ä]µ -§u¸ã·H×ùwÄoÿñƒè†ÛKÔB#ÈÍÜç¿åμ’ Se5I¯6^4ŸWzé’tK¸å~R¤9г 5#JX^à þ’M2á‡7ùtƒ3ÖD ~³ Ñ°`Œßh@#Ö j‡^ÁögWúçg’lžúÁ³xüƒçB” fÜáwð¤ÁrÏï€C`jjÓýçÂöýn´ VÚؼbìJü$’ãcd UôÐf,mMuÀAcbñ>¿µàõ “•+6°8ßb Qì ÖÞ”>4Wºæ’rŒÚ Úó µø+´€’ägÀ” øÿþ ŽÖF×ç6ŠÞ”…¾’?¥ö»6Ð¥†WWúågj·#”öœb™ÄYÄ3ô›tÌsÀÛWä¥ Õ[D Ësôþj”àwk€žm-+¶®÷Är±†®Øôk8K}@…’³•òq “…#ø·ø ¨ýcZ}äÖ-Áío8ÛK 5ù Íôw€ÍÛ•þøydçº`ÈgŠ3tyƒrÁ5‡à’Z uпµW°a¦iE»Q•…r,ðJÿÔĆè•Ü¼{çíJ¯üDÂQWÆ”e¶ -BSˆ¿ñXFèyЊø›bãå…ÖÏô† ¥E:¥·Ó^ò-Ø-ßWzåç’mÜl÷è5sJ¥÷&ÅÔÔËü»@ý[{m†©5sJ4‹ÑŸÈ5Ð+ò›¨5¢WˆÍÛ•^ù‰”›»¥>pÔ~ ´H,Áéwþ™i1Û üh¿«£F,Q0Ñj”Ý^j Ók`éB5s»ågnìì-š¶> Â@‰’kõwíUàmªA˜àw …ÀÔPª”AþRTrFAÔP{9P¼]ê•ŸF¶¡h+|¤,ætÀa¾+(e1ÿƒ[ï_°û!ò(¹C’~vš°yÐòq-8Í´©±ò¿RÍ-6¡ ²”¼‹’¢Éwó2n”õÌr+Îö lE¦TZ¼¡|¸£·G©ÍXÈ ¤Zò‹¾CØ.¤iB …2šgš -ßÆÍ”6Q3?QÈÍ0´ÐZèL3~SÜקdñÜtQ
©êqYu¼ÃÙŠ;žè6óú¼FÜwàFZ7´Vz§œ+.²d#KѲp¯œ)S#QËâ”Ë:ô c¥µÊµ÷VNk, -¿_ú˜¤/AŠßoбßW#SCéã~¹&G#ˆ9/ ï)•Œ6=EBK¼ÄE/7²°Ë”ûZ” Ó(º=:µAÐ@á(ŽHa5Oyƒ?…;׿@bµÑä”óÀ ‰op!mÄÛ0 “Û:±èÆKÙÒ¦½òn)ÌUrØÝpâqôß9ÊÿXnˆ«Ò,)ç÷HåÛ²¤r$.,¥ýj»ÇLap80uM>ºIåS;ÆÖ õë2ÞÚô’…Þxs[¦Â7¼óÜYêÅÔ˜”ü˯ë”òÁ”‘£Åð]ÀB7ò ¸$”iÝ°ÑU€ †ó: -`(Õï_ñLôææaç(8Ý^‡‰Ÿ•Îz ¿ýï$’WE~_ ü³ÒÎR”î •ò3˜é”+i+Ó•ÁÂK¾Õ H’4å-;¼ ŠÊ}Øeûd;*DÛ’sG3̆àù}M4°+.Ý6¥7€Þ´:ÝR?8é0qšðR.% ?À¢Î05Ðám»ç¶8î°+¶§æŽôÙö3ÿíÀY3YVŽÊ،┞þ`EA÷’;ñ-rÒü* $-XhtDkeÅ󘊿²yƒHížfÕon1Œ)w½ Ø6″FSÇæ-ÜÕ£á®Ð€WÊ}°j”´c? WÕBß¡’Éä -}ÑZaý…vrhÁ¯¬q@lahVÜÓ«‡Y߬ùì V±§Q?îõí!+’¾]7¡¶Ÿùfa!H4A°ðBC!6£@ácÁ¯ä2 Jš]y01c’`ÖÁ•Ԩ wBYµR(‘Š ³»ÙNî0ñìÄW”Püw-z†CÔzãö;œ¼}>;Ûœñ-N”æÖ8Ë ÌªP`×Ür3ÞAEmOÍ0{fâe×L¼v˜DY†™ßï°ÏZSÜþóó1Z8Û^6S_‡™_†Yž,ux£Ô¡@Ñ,;µ /›+ ŸP§è”QO¯Ðh6 I›3Ìχla(˜8Ùè~ÒΦüeá âvÕQGÓ VôÖî QºÃ%ŽJw¸Ä²BLepü#¤V›ð±ƒàWü2″´W8èq«`â»Ã,©_XæîQ5îʬ!nÔÊ$X’̃¯ñµÄ”B×¹;_Kž`¹w«™‰;;îç”7ó-Fp/3ê’ØR&”ÓÁŽÑ†»FSûò…ÉÔî±Uˆl’ȧt…q… ÑÁÂŽ(&Øé|ì ø•-DÆÖLG:ìhƒ Ø”K»‰AúÑp×hÄ#߬HÆvˆB$gØRb-}’yð’þ”¿²-±™XG#¸§Ös.O°lbÕ±ŽQ†»Bœ:ÿ° “Ä3 KAü5ñÜa*ó¿ßá¤ci†ùy³¶ŒA¯Üž™dnÍìÊWˆÏºP`W]x³R’Šš´MÌt˜xõ7§S9òwu†CѪâög˜ŸÏÑÂ%Øöf~V쨿³‰³*jŽnÄÕ°fÆÁøŠÙ”0³°íuš°‡[Ÿa~>§l›³C·ÃÌ®§ý}†£JQhe(°ënÁf>XÑ[F×»t×K)²1doC2É,ô™øºó±ƒàWâ2″¶¡YA.-¾^cÖízv!”À¨ ‹Fa›KÇ> î$+Bœ1!Öî{‘-(ñ`ßj1#šð#¤•¦ÀÎÇ’_ña@ošÝÚƒêjAë ÁÒ Fx½v1úÑp×(dšµF V$!5= ÊfØRÒhÁï›(Ñä ~±š,DçcÁ½âÒ€ð&öÑÒèÚ®úRÆ O°¹L’5êGÃ]£™¾”c@E0‹¿f˜ý3±”Å?”2;LBe;?Èû^½Ö·?ÃMó¶;賃J… Á½/¶e° ¥.¥ vå%ú”ˆ©d4é×9e”ò’8l‡ÿÎòÎ0tR·?Ãüü¦’¬*Ï¢ç7″öòÍÙ¾^Û°0″Ÿµ¡À®¼à|XPQ‹t””£ŽtàÔצ•×a†a-ßïpÒ’Ž´?Ãü¼Ð’þ«ö¶`ùÙÌHé0˳F›’ªÔ¡À®½óªÝµ [P/qºë%v’ä’WXà”±6fa†ùñ,²maæhX.Æ@f8뱫4¢À®@W=~°¢ç»ûe”x[âÈwoK,+ÉäG¯/4:”˜p§ó±ƒàWìÊ1ø¾’Y·KMƒ²¢ô£á®Qºìc€I7:_×/±µ´{@…q… ÑÁÂŽpÖ- ;~%†’l¸£Ä˜Bë ÁÂMˆh wÒ¥>X'”ܵFÀ·§LG’û×#šðkCZa ;~ÅçìÐXÚxª«ÁÆ -Vh0‹AúÑ°h”¾”úaA¥¾Õ:i8*©3Í6Ѹ’I-«$äýo:!íÏ0wÅê9NÁÜ·sç›õîܵ¥•¡À®;üŠò‡±r³¦XÄ?3Eü31Ûa¦ØùAÞï°1Bi†Y×K°°ó¶¯¼³}éu¸£`¶7ØÊ¢29Z ìÚËtù™µ%ÅN¦++¬™di ‹Ê/w8ëL”4>Ãü¼q Ïì›®b˜»’aîêe0 3ýY ìªK¸Bû`E?T Ö;ÃgL¼£$Sæ€N£#2Ï»¤6ácÁ¯Ø•#,¼Ín:êQ03¾é(G`D1ÊÔÊÑpWgl-ñ[X’Œƒã…ÒQv¼ÄUìŽ-ØV’+@§Ñ’C!Òžð±ƒàWŠë24+fL̺ X¸ Qtäcô£á®QH@k¬HBÆz@xù@±½‰|4’D/4:”˜È§ó±ƒàWR9Íùh³^L £i0″‰AúÑp×(䥵F V$!±=”t2·Â‹^)˜äòÃôÀï+Øì¾tvüJÌ”±œÜ¨ ˜+A0Û’`¹&DÔAQ†»2k`©ƒÁ0[o¾ˆ·&ž;LB1ÌRóûv&èáög˜ŸÎÂfòq²°#v:Lì:»î¯3TNG+C]wËÍL=ËÍø ø&m¶ðª7Ô¡ }UÌ*…¸É*ï7Ý}Ö·?ä«ôt˜û’aîë`lƒéuØé(G©CîúXé¢~×ðºZجշš*$Yyü2+o•:e†·rÞàK¾¦3œ6ô sa1w¦×EÁln0-ÅˬŒ>ˆ©1¯KZ”x×ë|áP ;_âªtçKl+ÉU†I Ó`ÍH+±ºG»ŠìˆÞ{²xåÞ÷¾]Þj’XĤ B(BÚh•ï!åÈŒ°~º”Äó Aâåa6è4XEÒJG”ð±úèf´Ày ÛÝ’`ƒ·¹±ú1)¨¨QéFûïË€¶ÃSûš°0¯$ž XBƒU$t”TB”li´K½ ››•dfL̺-âÖ4!E܇ “”Òj 6µNãͼPchgaãÎáTš’LbE;]Èû¬¦ßátÜ,µ¼ÚÖŠ‰~4’ù-iÐ,‹¥‰C}êô¥G¿kغì .› ⲉã”Ha˜2ø}V Óïp÷áè-½äl{;z±ØA&9GoáQ¡£ Æß¼1?³~Á÷# æ##¸ƒäœœž!~;Lâ8{ FÞgu0ýÛih†¹Ê™éEcï¾U93?&v˜å1UÚBÿX~0@GW)XøÝÀ‹!±tgL:º3&¦’¤ZÆIAh°^¤…XïæºÂÞؽ”ªcîXë ;Ìbš”m¡G-½:¥ée±¡Ð¢Ž fk&*B2ª>`B!@¹:¢ Þi4ÍôVXUÂÇ”[4Q@ØYmék8îcogÆeX k’-É*H]«ð©¨µÚïa}tEÈáÒêÚ×V’´ºöƒ1¤U¡ÁZ•V:Bꣶ`ºöÌbÆEEHu2w· ØBli·¦ÁâÛ³4{ “”ÒjÁòãñ®Ùä*B ‘H«¥×ó Aâ ‘P†Ã1½•ŽºèC”J3Q)HæÎÌØ×6A°p¶è»·rGA”PZÅ¿}ð»†3‡ùéÚCøÜŸ^¾)˜Ëvò÷Y5L¿ÃÙ݇‹%gNÕ.Y-¾ÌŽ9…«`§èЇÉk#÷bÄ$úX”…ß5Ì%ËÔ`ºÙnMâÉádçY`~ŸõÁô;œÂ}8{K¯8ÛžÑ_2’q;È£ždOÙì(#ÙXh‰r-®’ß5ìuê.52E9iCüv˜Ä‰rj†ÄöÔŒÐïpÈ÷a;”E©ºæö¸™ùÉf¸t˜å1UÛBÿX¡-¬ &àÚícD¼Äb
“(«hÁ?(“ðqál`äz¥2wf°’B°A’MÆVƒ÷VÄÑjÜèˉ#âÝ z³ ²Û†æÎj§ah«Ã$zŸt#䨤]”¦^-^³Í}(UËÜË’`;[Š©ûVÜÓ‹*eAÔ ‘M>ø]ÃÚÌœtÙaÒåj&ˆ³.;LªYåØë»o-ܶéæ6Yr×ês»fq6 ùcm¬}¿w=‹»%H9ÿű’Ý WHVmÃ-ƒïp½=œ‹ xzË©]ø8HLý1|»£ö#œ:EîKÆ2;€±³àbÝH0ÎöðYƒ à• ¥áëG`œ#¤Ôêa¦Ÿ+ëì÷§äh°FHXõÓ{ðežá'”>öµ&L©9^!Δ3W+¬1ðùvö.A¯Ã§OÖÚMop37ˆ¶v¦>Wk+9Ü(;µØTqQUyP`ŒMl‡”cùR…>©BgƒãúoP’HlUä x”ô¶†”ÑÖý†§²¤ jƒ3RÑ€…A.a8¶â²ö²oI&]eXUÓ¼³&ÌñîPã^v2X:I±³ø’nêiÉNÖg÷šv9UÅÚçŒôd¸-ÅÒÇu!Gs+Ù€,8ÙDÚDlbîíMŒ>âŽGäx±hdÐ Ù€%(c¯”2% xÈ,Íc¤N0´¼åA$”2™=yÂ7Q§A§Tx /K+”æ~Ç¿-¦AdVÉ «^z39¢’ì›ü2Ñ;ÉjÆ]°î¨‹›6Œ»Bð’$2ºÍ¶ë4ÁÇ”ºÎ®Ô¤GRÔ{oÁµ&mÅ” wpðú@8uö#Ö(ˆéÖ©€´TÄaÖ-®:¯´*›Œx”˜,£N8DšIÃéínð ‹p¢-žç!S1õÅ>¦à’;0qs’j~dPÂVP Z8½›Õ˜®p(jÈ3Ì.áæ1øõæO”zó6ܺx#fOüUã_qÊÄks’²_ç^f¿/vÀ3Û ÏlG2±™ÉÌÓŒPf¦f£2q5-‰œg>ϬÚ;QÖ*´ËFú*ƒ/#oxæ xÇHþÄ€¬xœøšŒh’àk0*Óß{Q]#N/|¿G…ë Onº®I®†¨p¥Úo§ O @7QFW¾¡zë€z玮þÜoýŠ²ÅÔ¼¨”è¡*éÛ¹2áÓ $y8B’©7œ`üB0Wª0ŒU>[A¤½P¥vsDÖ?.‡ ]Pá.Œì§*as8²èÃ|h°Ãt,¡SÈ 6ÑŽO5xd7þø PãnöJ8>Þ‹çhÊ’ÓMwÕÓP)ë6Àý@Zûpðî)¾oݒǸ¹^œ >9ô&öÁÕÛÍ||!GËÖUa¬»jÆÇÂl›ÀÜL®¬voݲ}¦ª¤fø3ËãBJdÛ°”XVRÙÛ†.Æa©‹ƒËfa˜¢€»Tr‹zõpFßÞëtS›‹¤7Á™ý^ù÷¶uÙm±ð¶÷^áè*I©°ÆA êàâSWõ’©¤Þ;vQº®zT_zDzÕžOà•eT]Š²öØb[ic#냛#•q&¨;RÆ[ᨌ®+S7~¸¯pQc®SÄöÚÐëCê#«Â7òÀ˜‡¦B”Í xp’G¿´Á’™Â²‡a)Ø5!Ù=5°÷” ±oc²ë”9±yÆÖâ9[‰k•9S®w¡.ßÜ _dÓDÜ;[P¿ˆ,LnjÈÓ™§ÜÕŒW®`”Û-šÈòå~§62x^k#§Íz2²dB§¡§îó¡©à>ãÞ»S.w²Äÿè0÷˜Fà €XÚ”Ø#ñœµÜˆÕY‰Æ9°¿ }·ÐCÛª¨%GÕÜßÇÜðqÂn ÉÓ)t•lë€Øƒÿ¬EŽµH†I‡ ù¯¨ÓáÃùÏ,0’mö»‹¤‡;æszûèˆVK«àÅÇ9¨Õ²²z4sí«¨§?ÐÔ£(}o¢#V£ÀƥŔ‘4YÙÚ– x”Í~fÞÒD´í…í zïÿ½‹¤4P´Äç:°ƒ§?³¤ÝvnEfútvࣛÌÚ2¡w#î=’5~?¾Øo#T9I¯O`Eµ½Hw{öã#’émËCÛÔýÁîLrÅgÉqR&ÓžWðÍ•Ÿ$¸nà`£Ú¸`éEtÇg©-mÉaÁWäÉÅñÔu’^Ž-‘É0hñ míàžnžÜæáøBãÇma”•œÌIr4‹·ƒµ˜ Øh0¥+}«”¶¸|]›uù6″%.€+àŽ:ÌF´° hýÓ-ÿkGJ( endstream endobj 31 0 obj > >> /Box [0 0 595 842] /Contents 32 0 R >> endobj 32 0 obj > stream x^ì½ËŠ.»’&8§Xã”庺;$ö>-†”tç3(j”Ô© ð¿ r’¯ßn7ÉL’_~ECA²Ù+¾pÿdf’ëj’þ÷Çÿþøãoÿå¯î‡sŸSX×ûÇÇôþû÷ÿñ1}®ëº ä~¤ä?}ü±Lù3þøÛëã¿þó4¹ßþ·û-¿üíãÿy‹jþœsC5=£Êî3´Tñ!UþK5…GTq þ˜×ð™¦òÑýÌûðûÏRü9Ãô3í?Òòó7@”ûùÈÑ”ÿôó7x,ü•~î{ø™òÏß `æ÷?à‹eÐû77Áfþƒ0qòkyî‰}nà*càs.,³Ø.Q÷Ï?]Öþ™:ôÇò(ÉýýÏØäÏÓ¸ë4ÈkÎÏð‡äÓï?}PöPY(5™s#×Å|zÿÏXŠX¬™ÿøéu:E&-tÅÛûsNã¢ü™KeZ’V¥#üTšKéÍ?×ƲFÚz”§á/”È^tŸø=¥ð¹ú_S#•æe³Pý¾îªy6PTF?W»w?9v8É%»¹¼Š¥ü-7ÿZ²~ÿ½°(·®&[ÊÔñ§_uëü(åˆëœ?ô75b•×kqq:Ç8•B+¥È-žbxRi¤Š-,ÖÜ]ÜÊrOö›ãrl¾)ÍgR‹1¹þ§wc?üå§sZ;Gßa¯í”B-Òô|Sê pþœæÓ:4ÏX eü&¤ú}·ƒó íõ?%’³È*ªNwû³ÅÑ9ÛüU’•(Ð*”ÓªÏúiœüôË?Ýjñ’^‰”·.öW¢ëÃ5R*g»_0×÷Ì÷±ä”«·-N’|ñò女ö†q>ù»þùDéuÁ R+=ìeÍ×TnJŸÎ·®çòw¸ ±#ïpíOtzM@;=¹YÕ éüŒt¿ÿ’fø‰%_þ0Mzæ ½ŸÝ9ûÀ(*EÍ0LõLPë?QÇóOØIûÇ• À¿ágîþü Á½jÒC·-½Žß€ÿíµ‹ÿsÿÿ_>vßÌÑýøæÿÿ¯çÓç’~Ì!~¦~ìúù3L€¤ÏèlÿzFè?]¼%”÷ãçêpÅBÜgZÓáHÃõsqåýýÑvÍöbxÈØìÏÆésÏáû qÝó&æ™Ýç2@1ŸÓ·ûÍçpRHçœ=¯¥íò9÷EæÕ¼šÅ0Mþ¯ÃÂwÅär’± ¡rëC*‡ƒM5=Ô*¥Ïäã-;TG¨óþÎ…+Ú´;úÏÁ).7ÈÂëþÄ- ªChrÒ0öþʼçÕ‰©TÀ¢ñDüº÷º0×æfP›Æk3]L8lÔ99*ùTËò9µ…ÞŽ?Ë{süÜÓŒ˜óÓgäþý¿üãñsP†èAçŸuëô™òÒûO’š{Ã-“ý×Æë’…ñV²Wk¦»~¹ ;¬|gS#NjÙÚ¢ô•Niâ§Ë}ü>íX¸•úÃ-á›zQÿ$¯ÐkîÉú”ûP0H’®HóŠup¤…û]Уѳ¿þæy¶U-üýø 5²§¥y⟉‡9ƒ”fzDˆþŠƒ•>i»«YÙÿ¨šOš¨Ï%]”FZŠ=%Ø
Источник
С одноатомным идеальном газом проводят циклический процесс, показанный на рисунке. За цикл газ совершает работу Aц = 5 кДж. Какое количество теплоты газ получает за цикл от нагревателя? Количество вещества газа в ходе процесса остаётся неизменным.
Одноатомный идеальный газ в количестве 10 моль сначала охладили, уменьшив давление в 3 раза, а затем нагрели до первоначальной температуры 300 К (см. рисунок). Какое количество теплоты получил газ на участке 2-3?



Задача 17
Давление насыщенного водяного пара при температуре 40 °С приблизительно равно 6 кПа. Каково парциальное давление водяного пара
в комнате при этой температуре при относительной влажности 30%?
Дано
Pн=6 кПа ф=30% P- ?
Ф=P*100%/Pн
P=Pн*30%/100%=6*0,3=1,8 кПа
Ответ P=1,8кПа
Задача 18
Для определения удельной теплоты плавления в сосуд с водой массой 300 г и температурой 20°С стали бросать кусочки тающего льда при непрерывном помешивании. К моменту времени, когда
лед перестал таять, масса воды увеличилась на 84 г. Определите по данным опыта удельную теплоту плавления льда. Ответ выразите в кДж/кг.
Уравнения количества теплоты Q(воды)=c(воды)*m(воды)*на дельта t и Q(льда)=лямбда(удельная теплота плав. льда)*m(льда). Приравниваем их получаем 4200*0.3*20=Лямбда*0.084, выражаешь лямбда=4200*0.3*20/0.084=300000=300кДж
Задача 19
В одном сосуде находится аргон, а в другом – неон. Средние кинетические энергии теплового движения молекул газов одинаковы. Давление аргона в 2 раза больше давления неона. Чему равно отношение концентрации молекул аргона к концентрации молекул неона?
Температура – это мера средней кинетической энергии молекул идеального газа а значит, оба газа находятся при одинаковой температуре. Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) термодинамической системы с микроскопическими (масса молекул, средняя скорость их движения) где – концентрация молекул газа.
Тогда отношение концентрации молекул аргона к концентрации молекул неона принимает значение:
Задача 20
В горизонтально расположенной трубке постоянного сечения, запаянной с одного конца, помещен столбик ртути длиной d = 15 см, который отделяет воздух в трубке от атмосферы. Трубку расположили вертикально запаянным концом вниз и нагрели на = 60 К. При этом объем, занимаемый воздухом, не изменился. Атмосферное давление = 750 мм рт.ст. Определите температуру воздуха в лаборатории.
Условие равновесия столбика ртути определяет давление воздуха в вертикальной трубке: , где – атмосферное давление. Здесь Н = 750 мм, – плотность ртути.
Поскольку нагрев воздуха в трубке происходит до температуры и объем, занимаемый воздухом, не изменился, то, согласно уравнению Клапейрона-Менделеева:
Окончательно получаем:К.
Задача 21
В запаянной с одного конца длинной горизонтальной стеклянной трубке постоянного сечения (см. рисунок) находится столбик воздуха длиной l1 = 30,7 см, запертый столбиком ртути. Если трубку поставить вертикально отверстием вверх, то длина воздушного столбика под ртутью будет равна l2 = 23,8 см. Какова длина ртутного столбика? Атмосферное давление 747 мм рт. ст. Температуру воздуха в трубке считать постоянной.
1. Когда трубка расположена горизонтально, объём воздуха и его давление равны, соответственно: , где S – площадь сечения трубки; , что вытекает из условия равновесия столбика ртути.
2. Когда трубка расположена вертикально отверстием вверх, объём закрытой части трубки и давление воздуха в ней равны, соответственно:
,
где ρ – плотность ртути.
3. Так как T = const, получаем: . , откуда (с учетом того, что 750 мм рт. ст. = 100 000 Па):
м
Задача 22
В горизонтальном цилиндре с гладкими стенками под массивным поршнем с площадью S находится одноатомный идеальный газ. Поршень соединён с основанием цилиндра пружиной. В начальном состоянии расстояние между поршнем и основанием цилиндра равно L, а давление газа в цилиндре равно внешнему атмосферному давлению p0 (см. рисунок).
Затем газу было передано количество теплоты Q, и в результате поршень медленно переместился вправо на расстояние b. Чему равна жёсткость пружины k?

Тепло, переданное газу, идёт на изменение его внутренней энергии и на совершением им работы:
В начальном состоянии давление и объём газа равны и в конечном состоянии – и Используя уравнение Менделеева – Клапейрона для изменения внутренней энергии получаем:
Чтобы рассчитать работу, заметим, что в каждый момент времени, когда поршень сдвинут на от начального положения давление равно т. е. давление линейно зависит от объёма. Значит, на pV-диаграмме процесс расширения будет изображён отрезком прямой, а фигура под графиком будет являться трапецией, площадь которой равна
Заметим, что этот результат можно получить, посчитав работу газа как минус сумму работ пружины и внешней атмосферы
В итоге
Источник
Условия 8 класса (город 2003)
Подробности Обновлено 31.03.2013 12:42
Условия задач городского тура 2003 года для 8 класса.
Первый этап.
Задача 1.
Определите диаметр цилиндрической бутылки, если в вашем распоряжении имеется следующее оборудование: два листа бумаги, карандаш, моток медной проволоки, амперметр, вольтметр, источник тока. Удельное сопротивление меди считать известным.
Задача 2.
В центре поршня массой 10 кг и площадью 500 см2 проделано тонкое отверстие. Известно, что если закрепить поршень в вертикальной трубе и налить поверх него воды до уровня 10 см, то за 1 с через отверстие в поршне вытечет 5 мл воды. В цилиндрический сосуд наливают воды до уровня 10 см и кладут сверху поршень. Поршень плотно прилегает к стенкам сосуда, но может двигаться без трения. Через какое время поршень достигнет дна сосуда?
Задача 3.
Имеется сосуд объемом 1 л и очень большой резервуар, наполненные водой. Температура воды в резервуаре равна комнатной TP = 20°C. Сосуд нагревают с помощью небольшого кипятильника мощности 50 Вт. При этом раз в 10 секунд с помощью небольшого шприца делают следующую операцию: набирают 10 мл из сосуда и переливают их в резервуар, затем сразу же набирают 10 мл из резервуара и переливают их обратно в сосуд. Постройте график зависимости температуры в сосуде от времени после многократного выполнения таких операций. Теплообменом сосуда с окружающей средой пренебречь.
Задача 4.
В вертикально расположенном сосуде с сечениями S1 и S2 (S1 = 9S2) находятся два невесомых поршня. Пространство между поршнями заполнено водой. Концы сосуда открыты в атмосферу. К верхнему поршню прикреплена пружина жесткостью k, к нижнему подвешен груз массой m. В начальный момент времени пружина не растянута, поршни закреплены, расстояние между поршнями h0. Найдите, на сколько просядет верхний поршень, если оба поршня отпустить.
Второй этап.
Задача 5.
В сосуд с водой насыпали некоторое количество соли, в результате чего через некоторый промежуток времени плотность получившейся жидкости стала с глубиной меняться по закону r = r0 + ah, где r0 = 1 г/см3, а a = 0,01 г/см4. В жидкость опустили два шарика, связанные нитью такой длины, что расстояние между центрами шариков не может превышать 15 см. Объем каждого шарика 1 см3, массы 1,2 г и 1,4 г. На какой глубине в равновесии находится каждый шарик? Нить считать невесомой и нерастяжимой.
Задача 6.
Сосуд наполнен водой до высоты h = 7,8 см. В него опустили два груза: шар массой M = 10 кг и радиуса h и половину такого же шара. Грузы привязаны к коромыслу AB длиной L = 1 м. Коромысло тянут вверх за некоторую точку O. Где должна располагаться точка O, чтобы грузы оторвались от дна одновременно? Плотность воды 1000 кг/м3, плотность материала грузов 5000 кг/м3. Считать, что второй груз плотно прижат ко дну и площадь его соприкосновения с дном сосуда 0,019 м2.
Задача 7.
На участке цепи, схема которого приведена на рисунке, включены резисторы с сопротивлениями R1 = 6 Ом, R2 = 3 Ом, R3 = 15 Ом, R4 = 8 Ом. Показания первого амперметра I1 = 0,1 А. Найдите показания второго амперметра.
Источник
Можаев В. Задачи с жидкостями //Квант. – 2006. – № 1. – С. 40-43.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
В этой статье будут рассмотрены задачи, в которых жидкость, с одной стороны, является средой, где находятся твердые тела, а с другой стороны, она, как жидкий элемент, участвует в движении, подобно твердому телу. Наиболее сложными являются комбинированные задачи, в которых жидкость движется вместе с находящимся в ней твердым телом (например, разобранная ниже задача 6).
Перейдем к обсуждению конкретных задач.
Задача 1. В цилиндрический сосуд с водой опустили кусок льда, в который вморожен осколок стекла. При этом уровень воды в сосуде поднялся на h = 11 мм, а лед остался на плаву, целиком погрузившись в воду. На сколько опустится уровень воды в сосуде после того, как весь лед растает? Плотность воды ρв = 1 г/см3, плотность льда ρл = 0,9 г/см3, стекла ρст = 2,0 г/см3
Обозначим первоначальный объем льда через Vл, а объем стекла – через Vст. Когда кусок льда полностью погрузился в воду, он вытеснил объем воды, равный
Очевидно, что этот же объем равен
где S – площадь поперечного сечения сосуда.
Теперь запишем условие плавания куска льда с вмороженным осколком стекла – суммарная сила тяжести льда и стекла равна выталкивающей силе:
Из совместного решения полученных уравнений найдем объемы льда и стекла:
Из растаявшего льда образовалась вода объемом
Поскольку кусок стекла остается в воде, понижение уровня воды в сосуде за время таяния льда будет равно
Задача 2. В вертикально расположенной трубке – с открытым верхним концом, с постоянным внутренним сечением и длиной 3L = 1080 мм – столбиком ртути длиной L заперт слой воздуха такой же длины. Какой длины столб ртути останется в трубке, если ее перевернуть открытым концом вниз? Внешнее давление p0 = 774 мм рт. ст.
Обозначим давление воздуха под ртутным столбиком в исходном положении трубки через p1. Тогда условие равновесия столбика ртути длиной L запишется в виде
где ρ – плотность ртути. Предположим, что после переворота трубки и установления первоначальной температуры часть ртути выльется. Обозначим через h длину столбика оставшейся в трубке ртути. Новое условие равновесия будет иметь вид
где p2 – новое давление воздуха над ртутным столбиком.
Условие сохранения количества изолированного воздуха позволяет записать
Подставляя сюда p1 из первого равенства, а p2 – из второго, получим уравнение относительно h:
или, если записать атмосферное давление в виде , где H0 = 774 мм:
Для данных численных значений L и H0 (в мм) получается, что
h = 270 мм.
Задача 3. U-образная трубка расположена вертикально и заполнена жидкостью. Один конец трубки открыт в атмосферу, а другой конец соединен с сосудом объемом V0 = 0,1 л, заполненным гелием (рис. 1). Объем всей трубки равен объему этого сосуда. В некоторый момент гелий начинают медленно нагревать. Какое минимальное количество теплоты необходимо подвести к гелию, чтобы вся жидкость вылилась из трубки? Атмосферное давление p0 = 105 Па; длины трех колен трубки одинаковы; давление, создаваемое столбом жидкости в вертикальном колене, равно p0/8.
Рис. 1
Обозначим полную длину трубки через 3L, а площадь внутреннего поперечного сечения трубки – S. Поскольку объем трубки V0, то длина каждого колена
Весь процесс нагрева гелия можно разбить на три участка. Первый участок – это когда жидкость еще находится в левом вертикальном колене. Рассмотрим момент времени, когда уровень жидкости в левом колене переместился на величину z, . Из условия равновесия жидкости в трубке найдем давление гелия:
где ρж – плотность жидкости. На втором участке, для которого , давление гелия
а на третьем участке, для
На рисунке 2 изображен график зависимости давления гелия от его объема V, который связан со смещением z простым соотношением:
На первых двух участках тепло необходимо подводить к гелию – это однозначно: здесь газ, расширяясь, совершает работу и одновременно нагревается. А вот третий участок неоднозначен: здесь газ также совершает работу, но при этом он может и охлаждаться. Убедимся, что и на этом участке тепло тоже подводится.
Учитывая, что , запишем уравнение процесса для третьего участка в виде
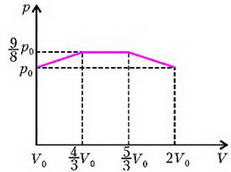
Рис. 2.
Рассмотрим малое изменение объема ΔV. Тогда работа, совершенная гелием, равна
Запишем уравнение состояния гелия как идеального газа:
где ν – количество вещества, Т – температура газа. Подставим в это уравнение выражение для давления на третьем участке процесса и получим
Продифференцируем обе части этого уравнения:
Теперь найдем изменение внутренней энергии гелия при изменении объема на ΔV:
Согласно первому началу термодинамики, подведенное количество теплоты равно сумме изменения внутренней энергии газа и совершенной им работы:
Легко убедиться, что при и
Итак, на всех участках тепло подводится, поэтому полное подведенное к гелию количество теплоты Q найдем как сумму полного изменения внутренней энергии и полной работы, которую совершил гелий:
Поскольку начальная и конечная температуры равны, соответственно,
то изменение внутренней энергии равно
Полную работу найдем как площадь под кривой на рисунке 2:
Тогда окончательно
Задача 4. «Тройник» с двумя открытыми в атмосферу вертикальными трубками и одной закрытой (горизонтальная трубка) полностью заполнен водой (рис. 3). После того, как тройник начали двигать по горизонтали в плоскости рисунка влево с некоторым постоянным ускорением, из него вылилась 1/16 массы всей воды. Чему при этом стало равно давление в жидкости у закрытого конца – в точке А? Трубки имеют одинаковые внутренние сечения. Длину L считать заданной. Диаметр трубок мал по сравнению с длиной L.
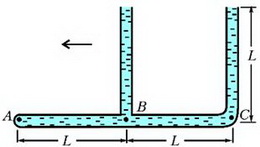
Рис. 3.
При движении тройника влево с ускорением а гидростатические давления в точках А, В и С (см. рис. 3) связаны между собой уравнением движения воды в горизонтальной трубке:
где ρ – плотность воды. Давление в точке С больше давления в точке В, поэтому вода будет выливаться из правой вертикальной трубки. Из условия неразрывности струи жидкость при этом будет отсасываться из левой вертикальной трубки. В установившемся режиме правая трубка будет полностью заполнена водой, а левая – частично. Поскольку вылилась 1/16 массы всей воды, что соответствует массе воды в части трубки длиной L/4, то в левой трубке останется столбик воды высотой 3/4L. Поэтому давления в точках В и С будут равны
где p0 – атмосферное давление.
Исключая из всех уравнений рB и рС, получим систему двух уравнений относительно рА и а:
Решая эту систему относительно рА, найдем
Задача 5. Тонкая, запаянная с одного конца и изогнутая под прямым углом трубка заполнена ртутью и закреплена на горизонтальной платформе, которая вращается с угловой скоростью ω вокруг вертикальной оси (рис. 4). При вращении платформы ртуть не выливается и полностью заполняет горизонтальное колено. Открытое колено трубки вертикально. Геометрические размеры установки указаны на рисунке; атмосферное давление р0; плотность ртути ρ. Найдите давление ртути у запаянного конца трубки.
Рис. 4.
Выделим в горизонтальной части трубки небольшой элемент ртути длиной dr, расположенный на произвольном расстоянии r от оси вращения (рис. 5).
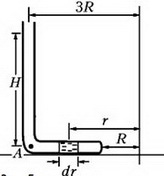
Рис. 5.
Этот элемент вращается в горизонтальной плоскости с угловой скоростью ω. Запишем уравнение движения выделенного элемента:
где S – площадь поперечного сечения трубки, dp – разность давлений между левым концом элемента ртути и правым. После сокращения на S получим связь между малыми приращениями dp и dr:
Проинтегрируем обе части этого уравнения и получим
Константу определим из условия, что при r = 3R (точка А) давление равно
и получим зависимость p(r)
Отсюда найдем давление ртути у запаянного конца трубки (r = R):
Задача 6. Стеклянный шар объемом V и плотностью ρ находится в сосуде с водой (рис. 6). Угол между стенкой сосуда и горизонтальным дном α, внутренняя поверхность сосуда гладкая, плотность воды ρ0. Найдите силу давления шара на дно сосуда в двух случаях: 1) сосуд неподвижен; 2) сосуд движется с постоянным горизонтальным ускорением а.
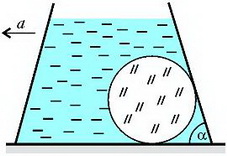
Рис. 6.
Сначала рассмотрим движущийся по горизонтали с постоянным ускорением а сосуд с водой. Введем систему координат XY, связанную с сосудом, как это изображено на рисунке 7.
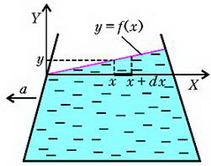
Рис. 7.
Наша задача – найти уравнение свободной поверхности жидкости в сосуде, который движется с горизонтальным ускорением а. Для этого выделим маленький элемент жидкости на оси Х, длина которого dx, а площадь поперечного сечения равна единице. С левого торца этого элемента давление равно
а с правого торца оно равно
где у – высота столба жидкости в точке х, а – аналогичная высота в точке . Так как наш элемент жидкости движется с ускорением а, его уравнение движения имеет вид
Отсюда получаем
или в интегральном виде –
Поскольку при х = 0 у = 0, константа тоже равна нулю, а уравнение свободной поверхности жидкости выглядит так:
Линии, параллельные свободной поверхности, внутри жидкости являются линиями постоянного давления. Таким образом, жидкость, движущаяся с горизонтальным ускорением а, эквивалентна неподвижной жидкости, находящейся в новом поле тяжести с эффективным «ускорением свободного падения», равным и направленным под углом к вертикали (рис. 8). Вертикальная составляющая этого эффективного ускорения равна обычному ускорению свободного падения g, а горизонтальная составляющая численно равна ускорению сосуда и направлена в противоположную сторону.
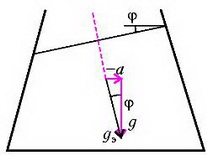
Рис. 8.
В том случае, когда сосуд неподвижен (а = 0), эффективное ускорение равно g и направлено по вертикали. Силы, действующие на стеклянный шар в этом случае, показаны на рисунке 9.
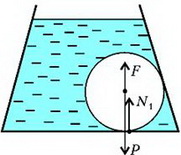
Рис. 9.
Здесь – вес (точнее – сила тяжести) шара, – выталкивающая сила, а N1 – сила реакции дна сосуда на шар. Из условия равновесия шара найдем, что
Очевидно, что сила давления шара на дно численно равна силе реакции дна и направлена в противоположную сторону.
В случае движущейся с горизонтальным ускорением a жидкости или неподвижной жидкости, но находящейся в поле с новым «ускорением свободного падения» gЭ, на шар будут действовать следующие силы (рис.10): вертикальная составляющая нового веса шара , горизонтальная составляющая этого веса , вертикальная составляющая выталкивающей силы , ее горизонтальная составляющая , реакция опоры Т со стороны боковой стенки и, наконец, сила N2 – сила реакции на шар со стороны дна сосуда. Запишем условие равновесия шара, т.е. равенство нулю всех сил, действующих на шар по вертикали:
и по горизонтали:
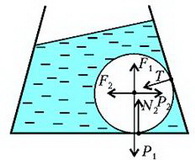
Рис. 10.
Исключая из этих уравнений Т, найдем искомую силу N2:
Разумеется, и в этом случае сила давления шара на дно сосуда численно равна силе реакции дна, но направлена в противоположную сторону.
Упражнения.
1. В цилиндрическом сосуде с водой плавает деревянная дощечка. Если на нее сверху положить стеклянную пластинку, то дощечка с пластинкой останутся на плаву, а уровень воды в сосуде повысится на Δh1. На сколько изменится уровень воды в сосуде с плавающей дощечкой, если ту же стеклянную пластинку бросить на дно сосуда? Плотность стекла ρст, плотность воды ρв.
2. U-образная трубка состоит из трех одинаковых колен, расположена вертикально и заполнена жидкостью (см. рис. 1). Один конец трубки соединен с баллоном, заполненным водородом, другой конец открыт в атмосферу. Водород в баллоне медленно нагревают, и он постепенно вытесняет жидкость из трубки. К моменту, когда из трубки вылилось 2/3 всей массы жидкости, водород получил количество теплоты Q = 30 Дж. Найдите объем баллона. Известно, что объем всей трубки равен объему баллона; атмосферное давление p0 = 105 Па; давление, создаваемое столбом жидкости в вертикальном колене трубки, равно p0/9.
3. «Тройник» из трех вертикальных открытых в атмосферу трубок полностью заполнен водой (рис. 11). После того, как тройник начали двигать в горизонтальном направлении в плоскости рисунка с некоторым ускорением, из него вылилось 9/32 всей массы воды. Чему равно ускорение тройника? Внутренние сечения трубок одинаковы, длина каждой трубки L.
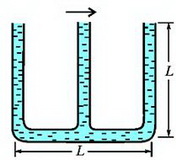
Рис. 11
4. Тонкая, запаянная с одного конца и изогнутая под прямым углом трубка заполнена жидкостью и закреплена на горизонтальной платформе, вращающейся с угловой скоростью ω вокруг вертикальной оси (рис. 12). Открытое колено трубки вертикально. Геометрические размеры установки указаны на рисунке; атмосферное давление p0; плотность жидкости ρ. Найдите давление жидкости у запаянного конца трубки.
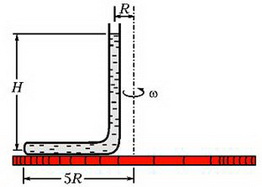
Рис. 12
Ответы.
1.
2.
3. .
4.
Источник
