В вертикальном цилиндрическом сосуде под тяжелым поршнем

В эту статью намеренно сведены задачи про газы в сосудах, закрытых поршнями – легкими и тяжелыми. Под влиянием нагрева газы меняют свое состояние и сдвигают поршни в новое состояние равновесия. Как правило, нужно определить сдвиг поршня или отношение объемов.

Задача 1. В закрытом цилиндрическом сосуде находится газ при нормальных условиях. Сосуд расположен горизонтально и разделен подвижным поршнем в отношении $frac{V_1}{V_2}=frac{1}{2}$ . В каком отношении поршень будет делить сосуд, если его меньшую часть нагреть до $t_1=127^{circ}C$ , а большую охладить до $t_2=-123^{circ}C$ ?

Понятно, что, раз поршень в равновесии, то давление одинаково с обеих сторон: .

уравнение состояния

К задаче 1

Состояние газа в левой части сосуда описывается уравнением:

Его количество пропорционально величине:

$[nu_1 R=frac{ p_1V_1}{ T_1}]$

Количество газа в правой части сосуда пропорционально:

$[nu_2 R=frac{ p_1V_2}{ T_1}]$

После изменения температур в левой части состояние газа таково:

$[p_2V_{1n}=nu_1 R T_2]$

А в правой:

$[p_2V_{2n}=nu_2 R T_3]$

Возьмем отношение двух последних равенств:

$[frac{ V_{1n}}{ V_{2n}}=frac{nu_1 R T_2}{nu_2 R T_3}=frac{nu_1R}{nu_2R}frac{ T_2}{ T_3}]$

То есть, подставляя и , получим:

$[frac{ V_{1n}}{ V_{2n}}=frac{frac{ p_1V_1}{ T_1}}{frac{ p_1V_2}{ T_1}}frac{ T_2}{ T_3}=frac{V_1 T_2}{V_2 T_3}=frac{127+273}{2(273-123)}=frac{4}{3}]$

Ответ: $frac{ V_{1n}}{ V_{2n}}=frac{4}{3}$

Задача 2. В закрытом цилиндрическом сосуде находится газ при температуре $t_1=0^{circ}C$ . Внутри сосуд перегорожен легким, не проводящим тепло поршнем радиуса см на две части объемами см и см. Поршень находится в равновесии. На какое расстояние переместится поршень, если большую часть газа нагреть на 30К? Температура в другой части не меняется.

Давление изначально одинаково с обеих сторон: .

уравнение состояния

К задаче 2

Состояние газа в левой части сосуда описывается уравнением:

А в правой части:

После того как газ нагрели, его давление и объем в обеих частях сосуда должны измениться, но по-прежнему давление слева и справа равны:

$[p_2V_{1n}=nu_1 R T_1]$

$[p_2V_{2n}=nu_2 R T_2]$

Возьмем отношение двух последних равенств:

$[frac{ V_{1n}}{ V_{2n}}=frac{nu_1 R T_1}{nu_2 R T_2}=frac{nu_1R}{nu_2R}frac{ T_1}{ T_2}]$

Количество газа в меньшей части сосуда пропорционально величине:

$[nu_1 R=frac{ p_1V_1}{ T_1}]$

Количество газа в правой части сосуда пропорционально:

$[nu_2 R=frac{ p_1V_2}{ T_1}]$

Тогда:

$[frac{ V_{1n}}{ V_{2n}}=frac{V_1 T_1}{V_2 T_2}]$

Так как объем равен произведению , то

$[frac{ l_{1n}}{ l_{2n}}=frac{V_1 T_1}{V_2 T_2}]$

$[frac{ l_1-Delta l}{ l_2+Delta l}=frac{V_1 T_1}{V_2 T_2}]$

Тогда

$[l_1-Delta l=frac{V_1 T_1}{V_2 T_2}( l_2+Delta l)]$

$[l_1-Delta l=frac{V_1 T_1}{V_2 T_2} l_2+frac{V_1 T_1}{V_2 T_2}Delta l]$

$[l_1-frac{V_1 T_1}{V_2 T_2} l_2=Delta l+frac{V_1 T_1}{V_2 T_2}Delta l]$

Но $frac{V_2}{L_2}=S$ , поэтому в левой части имеем:

$[l_1-frac{V_1 T_1}{S T_2}=Delta l+frac{V_1 T_1}{V_2 T_2}Delta l]$

И, так как $frac{V_1}{S}=l_1$ , то

$[l_1-frac{l_1 T_1}{ T_2}=Delta l left(1+frac{V_1 T_1}{V_2 T_2}right)]$

$[l_1left(1-frac{T_1}{ T_2}right)=Delta lleft(1+frac{V_1 T_1}{V_2 T_2}right)]$

Наконец,

$[Delta l=frac{ l_1left(1-frac{T_1}{ T_2}right)}{ 1+frac{V_1 T_1}{V_2 T_2}}]$

Но нам неизвестно, поэтому вместо этой величины используем отношение $frac{V_1}{S}$ :

$[Delta l=frac{V_1left(1-frac{T_1}{ T_2}right)}{ S+frac{S V_1 T_1}{V_2 T_2}}]$

$[Delta l=frac{10cdot10^{-6}left(1-frac{273}{ 303}right)}{picdot(0,02)^2+frac{picdot(0,02)^2 cdot10cdot273}{50cdot303}}=0,0067]$

Ответ: поршень сдвинется на 0,67 см.

Задача 3. Сосуд с газом плотно закрыт пробкой, площадь сечения которой см. До какой температуры надо нагреть газ, чтобы пробка вылетела из сосуда, если сила трения, удерживающая пробку, Н? Начальное давление воздуха в сосуде Па, начальная температура $t_1=-3^{circ}C$ .

Газ, находящийся в сосуде, изначально оказывает давление на пробку. Только его недостаточно для того, чтобы выдавить ее. Поэтому считаем, что избыточное давление, то есть изменение давления – как раз и выдавит пробку. Тогда

$[Delta p=frac{F}{S}]$

В свою очередь,

А так как процесс изохорный, то

$[frac{p_0}{T_1}=frac{p_1}{T_2}]$

Тогда

$[p_1=frac{p_0T_2}{T_1}]$

$[Delta p=p_1-p_0=frac{p_0T_2}{T_1}-p_0=p_0left(frac{T_2}{T_1}-1right)]$

Тогда

$[frac{F}{S}= p_0left(frac{T_2}{T_1}-1right)]$

Или

$[frac{F}{S}= p_0frac{Delta T}{T_1}]$

Откуда

$[Delta T=frac{F T_1}{S p_0}=frac{12cdot(273-3)}{2,5cdot10^{-4}cdot10^5}=127]$

Ответ: газ надо нагреть на $127^{circ}C$ , то есть до температуры $124^{circ}C$ .

Задача 4. В цилиндрическом сосуде с газом находится в равновесии тяжелый поршень. Масса газа и температура под поршнем и над ним одинаковы. Отношение объема над поршнем к объему под поршнем равно 3. Каким будет это отношение, если температуру в сосуде увеличить в 2 раза?

Рассмотрим состояние газа до нагрева. Температура обеих частей одинакова, массы равны, то есть

При этом понятно, что давления разные в обеих частях, так как объемы не одинаковы:

$[p_1+frac{mg}{S}=p_2]$

уравнение состояния

К задаче 4

Следовательно, так как $p_2=frac{ p_1V_1}{ V_2}$ , то

$[p_1+frac{mg}{S}=frac{ p_1V_1}{ V_2}]$

$[frac{mg}{S}=frac{ p_1V_1}{ V_2}- p_1=p_1left(frac{V_1}{ V_2}-1right)]$

Аналогично и после нагрева: так как газ нагревают в обеих частях сосуда, и масса газа в обеих частях одинакова, то можно записать, что

$[p_{1n}V_{1n}=p_{2n}V_{2n}]$

Искомое отношение –

$[frac{ V_{1n}}{ V_{2n}}=frac{ p_{2n}}{ p_{1n}}]$

$[p_{1n}+frac{mg}{S}=p_{2n}]$

$[frac{ V_{1n}}{ V_{2n}}=frac{ p_{1n}+frac{mg}{S}}{ p_{1n}}=1+frac{mg}{S p_{1n}}]$

Подставим давление поршня:

$[frac{ V_{1n}}{ V_{2n}}=1+frac{p_1}{p_{1n}}]$

Перейдем к объемам:

$[p_1=frac{nu R T_1}{V_1}]$

$[p_{1n}=frac{nu R T_2}{V_{1n}}]$

Подставим эти соотношения:

$[frac{ V_{1n}}{ V_{2n}}=1+frac{V_{1n}}{V_1}]$

Запишем объем после нагрева через приращение объема:

$[frac{ V_1-Delta V}{ V_2+Delta V}=1+frac{V_1-Delta V}{V_1}]$

$[frac{ V_1-Delta V}{ V_2+Delta V}=1+1-frac{Delta V}{V_1}]$

Перейдем к полному объему сосуда:

$[V_1=frac{V}{4}]$

$[V_2=frac{3V}{4}]$

$[frac{9}{16}V^2-Delta Vfrac{3V}{4}=2frac{V}{4}frac{3V}{4}+2frac{3V}{4}Delta V- Delta V frac{V}{4}-Delta V^2]$

Теперь мы имеем всего две неизвестных в одном уравнении, и можем разделить все уравнение, например, на :

$[frac{9}{16}- frac{3Delta V }{4V }=frac{6}{16}+frac{6Delta V }{4V} - frac{Delta V}{4V}-left(frac{Delta V}{V}right)^2]$

$[frac{3}{16}- frac{2Delta V }{V }+left(frac{Delta V}{V}right)^2=0]$

$[frac{3}{16}- 2a+a^2=0]$

Где $a=frac{Delta V}{V}$ – заметим, что корень должен быть меньше 1 по модулю и при этом положительный, иначе будет потерян физический смысл.

$[D=frac{sqrt{13}}{2}]$

$[a_1=1+frac{sqrt{13}}{4}]$

$[a_2=1-frac{sqrt{13}}{4}]$

Выбираем в связи с вышеизложенными соображениями второй корень. Тогда $Delta V= (1-frac{sqrt{13}}{4})V$ .

Найдем оба объема частей сосуда после подогрева:

$[V_{1n}=V_1-Delta V=frac{3V}{4}-(1-frac{sqrt{13}}{4}) V]$

$[V_{2n}=V_2+Delta V=frac{V}{4}+(1-frac{sqrt{13}}{4}) V]$

$[V_{1n}=- ( frac{V}{4}+frac{sqrt{13}}{4}) V=frac{V (sqrt{13}-1)}{4}]$

$[V_{2n}=V_2+Delta V=frac{5V}{4}-frac{sqrt{13}}{4}V=frac{V(5-sqrt{13})}{4}]$

Наконец, отношение объемов (Алилуйя! Мы сделали это!):

$[frac{ V_{1n}}{ V_{2n}}=frac{sqrt{13}-1}{5-sqrt{13}}]$

Источник

1. Воздушный шар объемом 2500 м3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. До какой минимальной температуры нужно нагреть воздух в шаре, чтобы шар взлетел вместе с грузом (корзиной и воздухоплавателем) массой 200 кг? Температура окружающего воздуха 7°С, его плотность 1,2 кг/м3. Оболочку шара считать нерастяжимой. (Решение)

2. Воздушный шар объемом 2500 м3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Рассчитайте максимальную массу груза, который может поднять шар, если воздух в нем нагреть до температуры 77°С. Температура окружающего воздуха 7°С, его плотность 1,2 кг/м3. Оболочку шара считать нерастяжимой. (Решение)

3.
Воздушный шар объемом 2500 м3 имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Если температура окружающего воздуха 7°С, а его плотность 1,2 кг/м3, то при нагревании воздуха в шаре до температуры 77°С шар поднимает груз с максимальной массой 200 кг. Какова масса оболочки шара? Оболочку шара считать нерастяжимой. (Решение)

4.
Воздушный шар имеет газонепроницаемую оболочку массой 400 кг и содержит 100 кг гелия. Какой груз он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па? Считать, что оболочка шара не оказывает сопротивления изменению объема шара. (Решение)

5.
Воздушный шар с газонепроницаемой оболочкой массой 400 кг заполнен гелием. Он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па, груз массой 225 кг. Какова масса гелия в оболочке шара? Считать, что оболочка шара не оказывает сопротивления изменению объема шара. (Решение)

В вертикальном цилиндрическом сосуде под тяжелым поршнем 6. При исследовании уравнения состояния газа ученик соединил сосуд (1) объемом 150 мл с манометром (2) тонкой трубкой и опустил сосуд в горячую воду (см. рисунок). Чему равна плотность воздуха в сосуде? Начальные показания манометра равны 0 мм рт. ст. Шкала манометра и нижняя шкала барометра (3) проградуированы в мм рт. ст. Верхняя шкала барометра проградуирована в кПа. Объем измерительного механизма манометра и соединительной трубки значительно меньше 150 мл. (Решение)

7. Теплоизолированный сосуд объемом V = 2 м3 разделен пористой неподвижной перегородкой на две равные части. Атомы гелия могут свободно проникать через поры в перегородке, а атомы аргона — нет. В начальный момент в одной части сосуда находится νHe = 2 моль гелия, а в другой — νAr = 1 моль аргона. Температура гелия TНe = 300 К, а температура аргона ТAr = 600 К. Определите температуру гелия после установления равновесия в системе. (Решение)

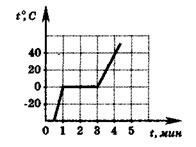В вертикальном цилиндрическом сосуде под тяжелым поршнем 8. На рисунке представлен график изменения температуры вещества в калориметре с течением времени. Теплоемкостью калориметра и тепловыми потерями можно пренебречь и считать, что подводимая к сосуду мощность постоянна. Рассчитайте удельную теплоемкость вещества в жидком состоянии. Удельная теплота плавления вещества равна 100 кДж/кг. В начальный момент времени вещество находилось в твердом состоянии. (Решение)

9. В цилиндрическом сосуде под поршнем длительное время находятся вода
и ее пар. Поршень начинают вдвигать в сосуд. При этом температура
воды и пара остается неизменной. Как будет меняться при этом масса
пара в сосуде? Ответ поясните.
(Решение)

10. В цилиндрическом сосуде под поршнем длительное время находятся вода
и ее пар. Поршень начинают вдвигать в сосуд. При этом температура
воды и пара остается неизменной. Как будет меняться при этом
отношение массы пара к массе жидкости в сосуде? Ответ поясните. (Решение)

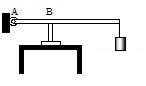В вертикальном цилиндрическом сосуде под тяжелым поршнем 11. В цилиндр объемом 0,5 м3 насосом закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии стержнем, который может свободно поворачиваться вокруг оси в точке А (см. рисунок). К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через 580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Площадь закрытого клапаном отверстия 5·10-4 м2, расстояние АВ равно 0,1 м. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите длину стержня, если его можно считать невесомым.
(Решение)

12. В цилиндр объемом 0,5 м3 насосом закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии стержнем, который может свободно поворачиваться вокруг оси в точке А (см. рисунок к зад. 11). К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через 580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Площадь закрытого клапаном отверстия 5·10-4 м2, расстояние АВ равно 0,1 м. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите длину AB. (Решение)

13. Воздушный шар имеет газонепроницаемую оболочку массой 400 кг и содержит 100 кг гелия. Какой груз он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па? Считать, что оболочка шара не оказывает сопротивления изменению объема шара.
(Решение)

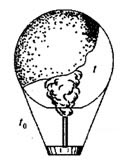
В вертикальном цилиндрическом сосуде под тяжелым поршнем
14. Воздушный шар, оболочка которого имеет массу М = 145 кг и объем V = 230 м3, наполняется горячим воздухом при нормальном атмосферном давлении и температуре окружающего воздуха t0 = 0°C. Какую минимальную температуру t должен иметь воздух внутри оболочки, чтобы шар начал подниматься? Оболочка шара нерастяжима и имеет в нижней части небольшое отверстие.

(Решение)

15. В высоком вертикальном цилиндрическом сосуде под тяжелым поршнем, способным перемещаться вдоль стенок сосуда практически без трения, находится некоторое количество воздуха под давлением p = 1,5 атм. Поршень находится в равновесии на высоте H1 = 20 см над дном сосуда. Определите, на какое расстояние ΔH сместится поршень, если сосуд перевернуть открытым концом вниз и дождаться установления равновесия. Считать температуру воздуха и атмосферное давление p0 = 1 атм постоянными. Массой воздуха в сосуде по сравнению с массой поршня можно пренебречь.
(Решение)

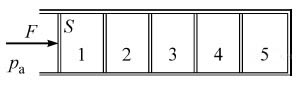В вертикальном цилиндрическом сосуде под тяжелым поршнем 16. Горизонтальный хорошо теплопроводящий цилиндр, разделённый подвижными поршнями площадью S = 100 см2 на 5 отсеков (№№ 1—5), содержит в них одинаковые количества идеального газа при температуре окружающей среды и под давлениями, равными давлению pа = 105 Па окружающей цилиндр атмосферы (см. рисунок). Каждый поршень сдвигается с места, если приложенная к нему горизонтальная сила превышает силу сухого трения Fтр = 2 Н. К самому левому поршню прикладывают горизонтальную силу F, медленно увеличивая её по модулю. Какого значения достигнет F, когда объём газа в самом правом, 5-м отсеке цилиндра уменьшится в n = 2 раза? Процессы изменения состояния газов в отсеках цилиндра считать изотермическими.
(Решение)

17. Горизонтальный хорошо теплопроводящий цилиндр, разделённый подвижными поршнями площадью S = 50 см2 на 5 отсеков (№№ 1—5), содержит в них одинаковые количества идеального газа при температуре окружающей среды и под давлениями, равными давлению pа = 105 Па окружающей цилиндр атмосферы (см. рисунок к зад 16). Каждый поршень сдвигается с места, если приложенная к нему горизонтальная сила превышает силу сухого трения Fтр = 4 Н. К самому левому поршню прикладывают горизонтальную силу F, медленно увеличивая её по модулю. Когда давление газа в самом правом, пятом отсеке цилиндра, увеличится в n = 3 раза? Процессы изменения состояния газов в отсеках цилиндра считать изотермическими.
(Решение)

18. Газ в цилиндрическом сосуде разделен на две равные части подвижным поршнем, имеющим массу m и площадь сечения S. При горизонтальном положении цилиндра давление газа в каждой половине сосуда равно p. Определить давление p1 газа над поршнем при вертикальном положении цилиндра. Температуру газа считать постоянной.
(Решение)

19. Сферическую оболочку воздушного шара делают из материала, квадратный метр которого имеет массу 1 кг. Шар наполняют гелием при атмосферном давлении 105 Па. Определите минимальную массу оболочки, при которой шар начнет поднимать сам себя. Температура гелия и окружающего воздуха одинакова и равна 0°С. (Площадь сферы S= 4πr2, объем шара V = 4/3πr3.)

(Решение)

20. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Площадь поперечного сечения поршня S = 30 см2. Давление окружающего воздуха p = 105 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. Какое количество теплоты нужно отвести от газа при его медленном охлаждении, чтобы поршень передвинулся на расстояние х = 10 см?
(Решение)

21. В горизонтальном цилиндрическом сосуде, закрытом подвижным поршнем, находится одноатомный идеальный газ. Давление окружающего воздуха р = 105 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. В процессе медленного охлаждения от газа отведено количество теплоты |Q| = 75 Дж. При этом поршень передвинулся на расстояние х = 10 см. Чему равна площадь поперечного сечения поршня?
(Решение)

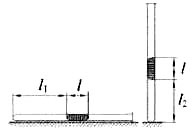В вертикальном цилиндрическом сосуде под тяжелым поршнем 22. В запаянной с одного конца длинной горизонтальной стеклянной трубке постоянного сечения (см. рисунок) находится столбик воздуха длиной l1 = 30,7 см, запертый столбиком ртути. Если трубку поставить вертикально отверстием вверх, то длина воздушного столбика под ртутью будет равна l2 = 23.8 см. Какова длина ртутного столбика? Атмосферное давление 747 мм рт. ст.
(Решение)

23. В водонепроницаемым мешок, лежащий на дне моря на глубине 73,1 м. закачивается сверху воздух. Вода вытесняется из мешка через нижнее отверстие, и. когда объём воздуха в мешке достигает 28,0 м, мешок всплывает вместе с прикреплённым к нему грузом массой 25,0 тонн. Определите массу воздуха в мешке в момент начала его всплывания. Температура воды раина 7°С. атмосферное давление па уровне моря равно 105 Па. Объёмом груза и стенок мешка пренебречь. Масса оболочки мешка неизвестна.
(Решение)

24. Сосуд разделен тонкой перегородкой на две части, отношение объёмов у которых V2/V1 = 3. В первой и второй частях сосуда находится воздух с относительной влажностью соответственно φ1 = 60% и φ2 = 70%. Какой будет влажность воздуха в сосуде, если перегородку убрать? Считать, что температура воздуха постоянна.(Решение)

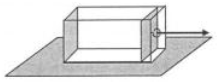В вертикальном цилиндрическом сосуде под тяжелым поршнем 25. В металлическом сосуде под поршнем находится воздух при атмосферном давлении (см. рисунок). Сосуд имеет массу 10 кг и расположен в горизонтальном положении на поверхности стола. Поршень может скользить без трения со стенками сосуда. Массон поршня и воздуха, заключённого в сосуде, можно пренебречь. За привязанный к нему шнур поршень очень медленно тянут в горизонтальном направлении. На сколько процентов возрастёт объём воздуха под поршнем к моменту, когда сосуд начнёт скользить по столу? Коэффициент трения покоя между сосудом и поверхностью стола равен 0,5. Площадь дна поршня 105 см2. Атмосферное давление 105 Па.
(Решение)

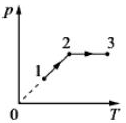В вертикальном цилиндрическом сосуде под тяжелым поршнем 26.Один моль одноатомного идеального газа совершает процесс 1-2-3, график которого показан на рисунке в координатах р-Т. Известно, что давление газа р в процессе 1-2 увеличилось в 2 раза. Какое количество теплоты было сообщено газу в процессе 1-2-3, если его температура Т в состоянии 1 равна 300 К, а в состоянии 3 равна 900 К?
(Решение)

27. Теплоизолированный цилиндр разделён подвижным теплопроводящим поршнем на две части. В одной части цилиндра находится гелий, а в другой – аргон. В начальный момент температура гелия равна 300 К,. а аргона – 900 К. Объёмы, занимаемые газами, одинаковы, а поршень находится в равновесии. Во сколько раз изменится объём, занимаемый гелием, после установления теплового равновесия, если поршень перемешается без трения? Теплоёмкостью цилиндра н поршня пренебречь.
(Решение)

Источник

Всероссийская олимпиада школьников по физике (2016 – 2017 уч.г.)
Школьный этап, 11 класс

Решения

Задача 1.

Тело брошено под углом ɑ к горизонту со скоростью Jо, причём максимальная дальность полёта равна максимальной высоте подъёма. Найти угол ɑ, если сопротивлением воздуха можно пренебречь.

(10 баллов)

Возможное решение
Запишем уравнение движения тела на ось ОХ и ОУ: Sмакс= х = (1); (2), где t – время полета тела вдоль оси ОХ. Решая совместно уравнения (1) и(2) получим , Þ . Нmax можно найти по формуле . По условию задачи Sмакс Þ; ; Þ Þ ; .
Критерии оценивания выполнения задания	Баллы
Приведено полное правильное решение, включающее следующие элементы: описаны все вновь вводимые в решении буквенные обозначения физических величин (; представлено полное верное объяснение с указанием наблюдаемых явлений и законов: ОХ: Sмакс= х = ОУ: Проведены необходимые математические преобразования и расчёты, приводящие к правильному ответу: .	1 1 1 1 2 1 2 1

Задача 2.

Вертикальный цилиндрический сосуд содержит под тяжелым поршнем массой М некоторое количество гелия. Какое количество тепла Q необходимо сообщить газу, чтобы его объем увеличился вдвое? Как изменится результат, если под поршнем будет находиться водород? Потерями тепла и внешним давлением пренебречь.

В вертикальном цилиндрическом сосуде под тяжелым поршнем

(10 баллов)

Возможное решение
Процесс расширения газа происходит при постоянном давлении, поэтому Q = ucрDТ, где u – количество молей газа, cр – теплоемкость газа при постоянном давлении. cр = cv + R, где cv – теплоемкость газа при постоянном объеме. Для гелия (одноатомный газ) cv =, cр =; для водорода (двух атомный газ) cv =, cр =. Газ находится при постоянном давлении р = (S – площадь сечения сосуда) и подчиняется уравнению состояния рV = uRT. Таким образом , Q = ucрDТ = . Для гелия Q1 = , для водорода Q2 =
Критерии оценивания выполнения задания	Баллы
Приведено полное правильное решение, включающее следующие элементы: описаны все вновь вводимые в решении буквенные обозначения физических величин; представлено полное верное объяснение с указанием наблюдаемых явлений и законов: Q = ucрDТ для гелия cv =, cр = для водорода (двух атомный газ) cv =, cр = р = уравнение состояния рV = uRT Проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу: Q = Для гелия Q1 = для водорода Q2 =	1 1 1 1 1 1 2 1 1

Задача 3.

Имеется источник тока с внутренним сопротивлением r = 20 Ом. Какое внешнее сопротивление нужно подключить к источнику, чтобы мощность, выделяющаяся на внешнем сопротивлении, отличалась от максимально возможной мощности на 25 %?

(10 баллов)

Возможное решение
Тепловая мощность, выделяющаяся на резисторе, имеющем сопротивление R, определяется законом Джоуля – Ленца P=UI , где I – сила тока в цепи, а U – напряжение на резисторе. Сила тока определяется законом Ома для полной цепи , а напряжение на резисторе – законом Ома для участка цепи U = IR Þ Мощность, выделяющаяся на внешнем сопротивлении P = I2R = Она будет максимальной при условии R = r Þ По условию задачи мощность, выделяющаяся на внешнем сопротивлении, отличалась от максимально возможной мощности на 25 % Þ P = 0,75 Pmax Þ Подставляя в полученную формулу числовые данные, находим Получили квадратное уравнение корнями которого являются: R1= 6,7 Ом; R 2= 60 Ом.
Критерии оценивания выполнения задания	Баллы
Приведено полное правильное решение, включающее следующие элементы: описаны все вновь вводимые в решении буквенные обозначения физических величин; представлено полное верное объяснение с указанием наблюдаемых явлений и законов (законы Ома для участка цепи и полной цепи, закон Джоуля-Ленца): U = IR P = Мощность максимальна при условии R = r Проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу: P = 0,75 Pmax Представлен правильный ответ с указанием единиц измерения искомой величины R1= 6,7 Ом; R 2=60 Ом.	1 1 1 1 1 1 1 1 2

В вертикальном цилиндрическом сосуде под тяжелым поршнем

Из за большого объема этот материал размещен на нескольких страницах:

1 2 3 4 5 6

Источник