В закрытом сосуде находится 1 моль идеального одноатомного газа

По первому закону термодинамики [Q=Delta U+A,quad (1)] (Q) – количество теплоты, полученное системой, (Delta U) – изменение внутренней энергии, (A) – работа газа.
А количество теплоты, полученное системой равно [Q=Lm,quad (2)] где (m) – масса образовавшегося пара.
Так как процесс испарения прошел не до конца, то данный процесс изотермический, а значит работа газа будет совершаться за счет изменения массы пара [A=dfrac{m}{M}RT,quad (3)] где (T) – температура газа в Кельвинах.
Объединим (1), (2) и (3) и найдем отношение (dfrac{Delta U}{Q}) [dfrac{Delta U}{Q}=dfrac{Q-A}{Q}=1-dfrac{dfrac{m}{M}RT}{Lm}=dfrac{RT}{LM}=dfrac{8,31 text{ Дж/(К$cdot$моль)}cdot (273+80)text{ К}}{396cdot 10^3text{ Дж/кг}cdot 78cdot 10^{-3}text{ кг/моль}}approx 90,5 %]

Ответ: 90,5

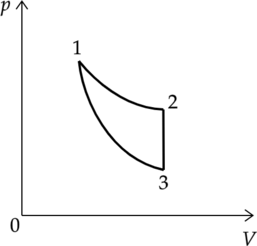
Процессы:
1-2 — изотермический
2-3 — изохорный
3-1 — адиабатический
КПД тепловой машины равен: [; ; ; ; eta = dfrac{A_text{ц}}{Q_text{н}} ; ; ; ; (1)] где (A_text{ц}) — работа, совершенная газом за цикл, (Q_text{н}) — количество теплоты, полученное газом от нагревателя.
Работа газа за цикл есть сумма работ газа в каждом процессе: [A_text{ц} = A_{1-2} + A_{2-3} + A_{3-1}] Так как в процессе 2-3 объем газа постоянен, то его работа равна нулю.
Тогда работа газа за цикл равна: [; ; ; ; A_text{ц} = A_{1-2} + A_{3-1} ; ; ; ; (2)] Далее необходимо найти количество теплоты (Q_text{н}), полученное газом от нагревателя.
Для этого запишем первое начало термодинамики для каждого процесса.
Процесс 1-2: [Q_{1-2} = A_{1-2} + Delta U_{1-2}] Так как процесс 1-2 изотермический, то изменение внутренней энергии газа (Delta U_{1-2}) равно нулю.
Объем газа увеличивается, следовательно, газ совершает положительную работу.
Отсюда получаем, что: [Q_{1-2} = A_{1-2} > 0 ; ; ; Rightarrow ; ; ; ; Q_{1-2} > 0] Процесс 2-3: [Q_{2-3} = A_{2-3} + Delta U_{2-3}] Так как процесс 2-3 изохорный, то работа газа (A_{2-3}) равна нулю.
Давление газа уменьшается, следовательно, его температура также уменьшается (для изохорного процесса (p sim T)).
Следовательно, изменение внутренней энергии газа отрицательно.
Отсюда получаем, что: [Q_{2-3} = Delta U_{2-3} < 0 ; ; ; Rightarrow ; ; ; ; Q_{2-3} < 0] Процесс 3-1:
Так как процесс 3-1 адиабатный, то (Q_{3-1} = 0): [; ; ; ; Q_{3-1} = A_{3-1} + Delta U_{3-1} ; ; ; Rightarrow ; ; ; ; A_{3-1} = – Delta U_{3-1} ; ; ; ; (3)] Таким образом, количество теплоты, полученное газом от нагревателя равно: [Q_text{н} = Q_{1-2}] [; ; ; ; Q_text{н} = A_{1-2} ; ; ; ; (4)] Подставим (2), (4) в (1): [eta = dfrac{A_{1-2} + A_{3-1}}{A_{1-2}}] [; ; ; ; eta = 1 + dfrac{A_{3-1}}{A_{1-2}} ; ; ; ; (5)] Подставим (3) в (5): [; ; ; ; eta = 1 – dfrac{Delta U_{3-1}}{A_{1-2}} ; ; ; ; (6)] Изменение внутренней энергии газа в процессе 3-1 равно: [; ; ; ; Delta U_{2-3} = dfrac{3}{2}nu R(T_1 – T_3) ; ; ; ; (7)] где (R) — универсальная газовая постоянная.
Подставим (7) в (6) и выразим искомую температуру: [eta = 1 – dfrac{dfrac{3}{2}nu R(T_1 – T_3)}{A_{1-2}}] [T_3 = T_1 – dfrac{2}{3nu R} (1 – eta)A_{1-2}] Температура (T_1) является максимальной в этом цикле, так как точка 1 на графике принадлежит изотерме 1-2, которая лежит выше, чем изотерма, проведенная через точку 3: (T_1 = T_o).
Следовательно, температура (T_3) является минимальной: (T_3 = T).
Работа (A_{1-2}) совершена газом в изотермическом процессе: (A_{1-2} = A).
Таким образом, искомая температура равна: [T = T_o – dfrac{2}{3nu R} (1 – eta)A]

Ответ: $T=T_o-dfrac{2}{3nu R}(1-eta)A$

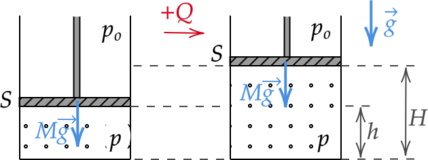
Рассматриваемый процесс — изобарный (так как поршень подвижный и количество вещества газа не изменяется).
Запишем первое начало термодинамики для изобарного процесса: [; ; ; ; Q = A+Delta U ; ; ; ; (1)] где (A) — работа газа, (Delta U) — изменение внутренней энергии газа.
Работа газа и изменение его внутренней энергии равны: [; ; ; ; A = pDelta V ; ; ; ; (2) ; ; ; ; ; ; ; ; ; ; ; Delta U = dfrac{i}{2}nu RDelta T ; ; ; ; (3)] где (p) — давление газа под поршнем, (Delta V) — изменение объема газа, (i) — число степеней свободы (для одноатомного газа (i = 3)), (nu) — количество вещества газа, (R) — универсальная газовая постоянная, (Delta T) — изменение температуры газа.
Подставим (2), (3) в (1): [Q = pDelta V + dfrac{3}{2}nu RDelta T] Для изобарного процесса справедливо равенство: (pDelta V = nu RDelta T).
Тогда уравнение (4) примет вид: [; ; ; ; Q = pDelta V + dfrac{3}{2}pDelta V = dfrac{5}{2}pDelta V ; ; ; ; (5)] Давление внутри сосуда складывается из атмосферного давления и давления, оказываемого поршнем (так как у него есть масса): [; ; ; ; p = p_o + dfrac{Mg}{S} ; ; ; ; (6)] где (g) — ускорение свободного падения.
Изменение объема, занимаемого газом, после сообщения теплоты равно: [; ; ; ; Delta V = (H-h)S ; ; ; ; (7)] Подставим (6), (7) в (5) и выразим высоту, на которой будет находиться поршень над дном цилиндра: [Q = dfrac{5}{2}left( p_o + dfrac{Mg}{S} right) (H-h)S] [H=h+dfrac{2Q}{5(p_oS+Mg)}]

Ответ: $H=h+dfrac{2Q}{5(p_oS+Mg)}$

Так как сосуды теплоизолированные, а газ не совершает работы, то изменение внутренней энергии равно 0, то есть [U_1+U_2=U] где (U_1) – внутренняя энергия первого сосуда, (U_2) – внутренняя энергия второго сосуда, (U) – внутренняя энергия сосудов после открытия краника.
Или [dfrac{3}{2}nu_1R T_1+dfrac{3}{2}nu_2RT_2=dfrac{3}{2}left(nu_1+nu_2right)RT] Отсюда установившаяся температура [T=dfrac{nu_1T_1+nu_2T_2}{nu_1+nu_2}] По закону Клапейрона – Менделеева [p2V=left(nu_1+nu_2right)RT] Отсюда объем одного сосуда [V=dfrac{left( nu_1T_1+nu_2T_2right)R}{2p}=dfrac{left( 3text{ моль} cdot 350text{ К}+2text{ моль} cdot 400text{ К}right)cdot 8,31 text{ Дж/(моль$cdot$ К)}}{2cdot 6cdot 10^3 text{ Па}}approx 1,28text{ м$^3$ }]

Ответ: 1,28

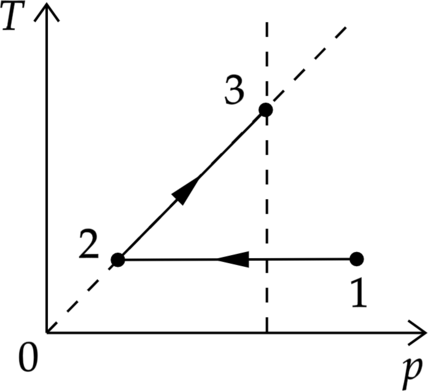
1. Воспользуемся первым законом термодинамики [Q=Delta U+A,] где (Q) – количество теплоты, полученное системой, (Delta U) – изменение внутренней энергии системы, (A) – работа газа.
Так как процесс изохорный, то работа газа равна 0. Распишем изменение внутренней энергии и получим [Q=dfrac{3}{2}nu R Delta T=dfrac{3}{2}nu R left(T_3-T_2right)] 2. Воспользуемся законом Шарля [dfrac{p_2}{T_2}=dfrac{p_3}{T_3} Rightarrow T_3=dfrac{p_3 T_2}{p_2}=3T_2] 3. По условию процесс 1–2 изотермический, значит [T_1=T_2] Следовательно, первый закон термодинамики выглядит [Q=dfrac{3}{2}nu R left(3T_1-T_1right)=3nu R T_1= 3cdot 1 text{ моль} cdot 8,31 text{ Дж/(моль $cdot$ К)}cdot 100text{ К}=2493text{ Дж}]

Ответ: 2493

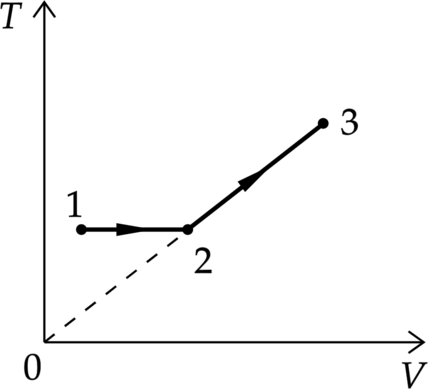
1.Проанализируем процессы
1–2 Процесс изотермический, по закон Бойля-Мариотта [p_1 V_1=p_2V_2] Значит возрастает объем и давление.
2–3 Температура увеличивается линейно объему, следовательно, процесс изобарный.
2. Количество теплоты, полученное в процессе 1–2–3, равно сумме количеств теплоты, полученных в процессах 1–2 и 2–3. [Q_{123}=Q_{12}+Q_{23}] 3. По первому закону термодинамики [Q=Delta U +A,] где (Q) – количество теплоты, полученное системой, (Delta U) – изменение внутренней энергии системы, (A) – работа газа.
Значит в процессе 1–2 изменение внутренней энергии равно 0, а количество теплоты [Q_{12}=A_{12}=3 text{ кДж}] В процессе 2–3 по условию объем возрос в 2 раза, значит по закону Гей-Люссака [dfrac{V_2}{T_2}=dfrac{V_3}{T_3}Rightarrow T_2=dfrac{V_2 T_3}{V_3}= dfrac{600text{ К}}{2}=300text{ К}] По закону Клапейрона–Менделеева [pV=nu R T] Значит количество теплоты, полученное в процессе 2–3 равно [Q_{23}=dfrac{3}{2}nu R left(T_3-T_2right)+pleft( V_3-V_2right)=dfrac{3}{2}nu R left(T_3-T_2right)+nu R left(T_3-T_2right)=dfrac{5}{2}nu R left(T_3-T_2right)] [Q_{23}=dfrac{5}{2}cdot 1 text{ моль} cdot 8,31 text{ Дж/(моль $cdot$ К)}left( 600 text{ К}- 300text{ К}right)= 6232,5 text{ Дж}] А общее количество теплоты [Q=Q_{12}+Q_{23}=6232,5 text{ Дж}+ 3000text{ Дж}=9232,5 text{ Дж}]

Ответ: 9232,5

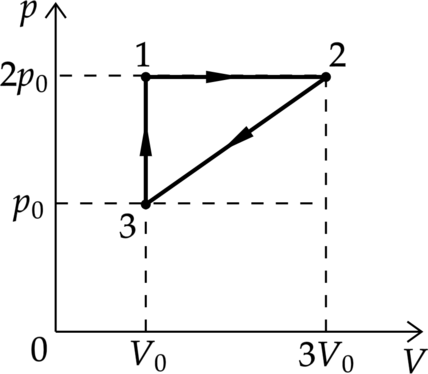
Работа внешних сил в процессе 2–3 равна площади под графиком. [A_{23}=dfrac{p_0+2p_0}{2}left(3V_0-V_0right)=3p_0V_0] (p) – давление, (V) – объем газа, (nu) – количество вещества, (T) – температура газа в Кельвинах.
Воспользуемся первым законом термодинамики [|Q_{text{ хол}}|=|Q_{23}|=Delta U_{23}+A_{32}=dfrac{3}{2}left( nu R T_2 -nu R T_3right)+ 3p_0V_0quad (1)] Также по уравнению Клапейрона – Менделеева [p_2V_2=nu R T_2= 2p_0 cdot 3V_0 =6p_0V_0 quad (2)] [p_2V_2=nu R T_3=p_0V_0 quad (3)] Подставим в (1) формулы (2) и (3) [|Q_{text{ хол}}|=dfrac{3}{2}left(6p_0V_0-p_0V_0right)+3p_0V_0= dfrac{21}{2}p_0V_0=dfrac{7}{2}A_{23}=3,5 cdot 5text{ кДж} =17,5text{ кДж}]

Ответ: 17,5